BP神经网络通俗教程（matlab实现方法）

BP神经网络通俗教程（matlab实现方法）

BP神经网络是什么

BP（Back-propagation，反向传播）神经网络是最传统的神经网络。当下的各种神经网络的模型都可以看做是BP神经网络的变种（虽然变动很大…）。
这东西是干什么用的呢？
我们在现实中要处理的一切问题映射到数学上只分为两类，可归纳的问题与不可归纳的问题。首先什么是不可归纳的问题，举个例子，你不能用一套完美的数学公式去表达所有的质数 ， 因为目前的研究表明，还没有什么方法是能够表达质数的，也就是说，质数的出现，本身不具备严格的数学规律，所以无法归纳。
但是我们人眼看到猫猫狗狗的图片就很容易分辨哪个是猫，哪个是狗。这说明在猫和狗之间，确实存在着不同，虽然你很难说清楚它们的不同到底是什么，但是可以知道，这背后是可以通过一套数学表达来完成的，只是很复杂而已。
大部分AI技术的目的就是通过拟合这个复杂的数学表达，建立一个解决客观问题的数学函数。BP神经网络的作用也是如此。
BP神经网络这个名字由两部分组成，BP（反向传播）和神经网络。神经网络是说这种算法是模拟大脑神经元的工作机理，并有多层神经元构成的网络。
而这个名字的精髓在BP上，即反向传播。反向传播是什么意思呢。这里举个例子来说明。
比如你的朋友买了一双鞋，让你猜价格。
你第一次猜99块钱，他说猜低了。
你第二次猜101块钱，他说猜高了。
你第三次猜100块钱，他说猜对了。
你猜价格的这个过程是利用随机的数据给出一个预测值，这是一个正向传播。
而你的朋友将你的预测值与真实值进行对比，然后给出一个评价，这个过程是一个反向传播。
神经网络也是类似的过程，通过对网络的超参数进行随机配置，得到一个预测值。这是一个正向传播的过程。而后计算出预测值与真实值的差距，根据这个差距相应的调整参数，这是一个反向传播的过程。通过多次迭代，循环往复，我们就能计算出一组合适的参数，得到的网络模型就能拟合一个我们未知的复杂函数。
我们来看这个BP神经网络的示意图

其中蓝色的箭头是正向传播的过程，黄色的线条就是反向传播。

BP 神经网络的具体描述

BP神经网络的拓扑结构

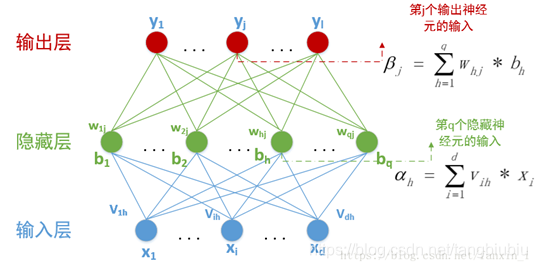
上面这张图是BP神经网络的拓扑结构。简而言之就是分为三个“层”。输入层、隐藏层和输出层（一般情况下隐藏层会有若干层，这里只画了一个隐藏层）。每个层都包含若干个神经元（图中圆形）。上一层的输出作为下一层输入（数据的联系如图中连线所示）

单个神经元

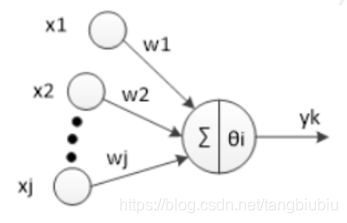
单个的神经元如上图所示。$x_i$为输入，$w_i$代表权重，${\theta }_i$代表阈值。$y_k$代表输出。这里还有一个偏置$b$和激活函数$f（x）$没有画出。总之，一个神经元需要四个参数和一个函数才能得到输出（输入、权重、阈值、偏置还有激活函数）

具体数学表达为：
$ne{t}_i={\sum }_{i=0}^n{x}_i{w}_i=x_1{w}_1+x_2{w}_2...$
如果这个$ne{t}_i$大于${\theta }_i$，那么这个神经元被激活，继续运算
反之这个神经元关闭，没有输出
激活后做如下运算：
$y_k=f（ne{t}_i+b）$
这样就求得了这个神经元的输出。

激活函数$f（x）$

在单个神经元中的$f（x）$是激活函数。下图是三种常用的激活函数。

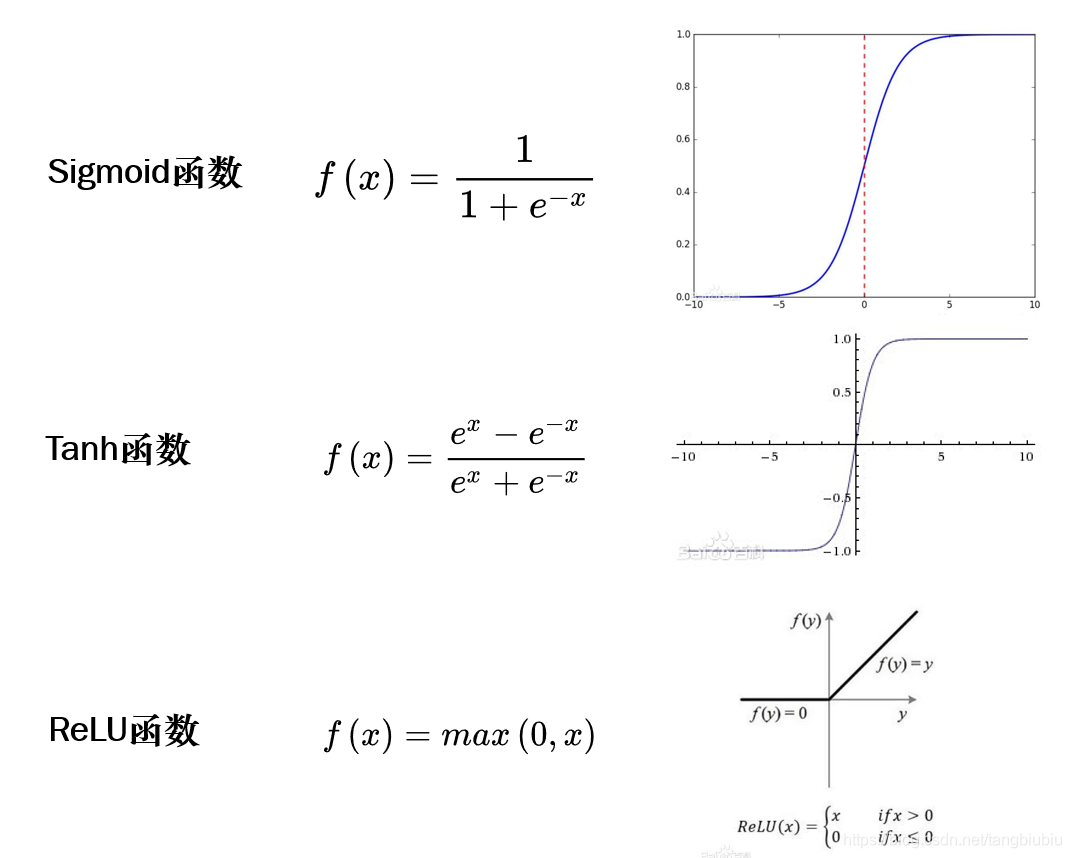
为什么要使用激活函数呢？
激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。
如果没有激活函数，无论网络有多少层，输出都只能是输入的线性组合，这样就形成了原始的感知机。

反向传播

反向传播是这个算法的精髓！上文已经形象的说明了反向传播的大致原理。下面我们来看反向传播具体是怎么运行的。
就像猜价格游戏一样，通过不断调整你猜的价格，使得预测的价格接近真实的价格。
我们希望通过调整权重$w$，使得预测值$o$与真实值$t$的差距缩小。
那么首先我们需要先定义预测值$o$与真实值$t$的差距，我们用损失函数（loss function）来衡量。
下面列出了几种常用的损失函数：

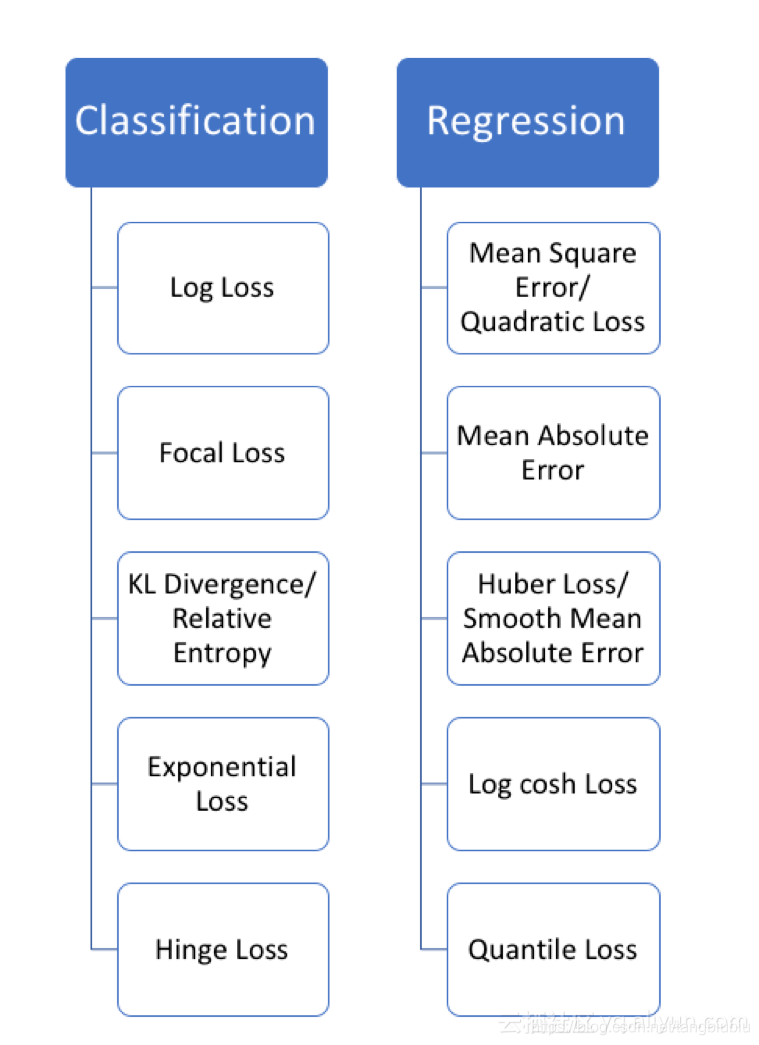
左边是解决分类问题时常用的损失函数，右边是解决回归问题时常用的损失函数。具体函数的公式我就不写了，你们具体要用的时候直接按照名字百度一下就好。
这边只提一下均方误差损失函数（MSE），因为下文要以他为例子：$E=1/2(o-t{)}^2$
其中$E$代表ERORR值，也叫LOSS值。是衡量误差的指标。
再说一遍，我们的目的就是通过调整权重$w$让$E$尽可能的小。所以我们建立权重$w$和$E$的函数，把权重$w$看作自变量，把$E$看作因变量。求出导数。利用梯度下降的原理使$E$沿着越来越小的方向下降。
推导过程：

这里的误差函数就是均方误差（MSE），梯度下降的公式中$\eta$代表学习率，是人为设定的一个参数。$\Delta w_{ji}$我们要调整权重的改变值。
输出层求解步骤如下，注意理解Step2是对LOSS函数求偏导，Step3是对激活函数求偏导。

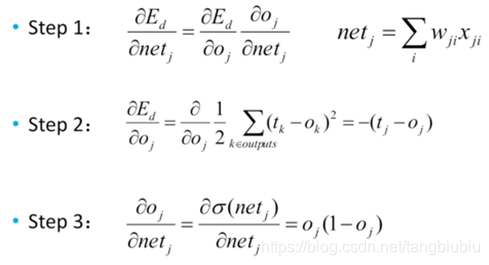
结果带入梯度下降公式可得：

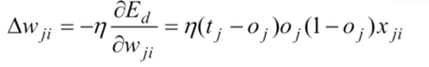
隐藏层求解步骤：

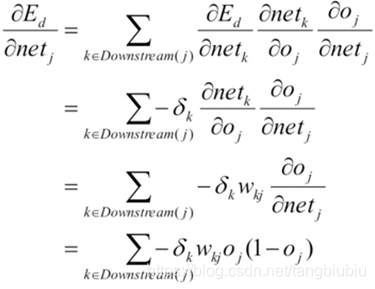带入梯度下降公式可得：

根据求得的结果相应的调整权重$w$就完成了一次反向传播。
然后开始下一次迭代，循环往复，直至达到收敛条件，跳出循环。

BP神经网络的基本运行原理就介绍完了。

神经网络的Matlab实现

Matlab自带神经网络的工具包，所以实现的这个环节还是非常简单的。我以Matlab2020为例演示一下。（示例数据和题目来自“清风数学建模”）
例题如下：
给出的数据保存在一个EXCEL文档中。截图了一小部分：

首先我先将数据导入到Matlab的变量中，X代表训练集和验证集的吸光度数据，Y代表训练集和验证集的辛烷值。new_X代表测试集
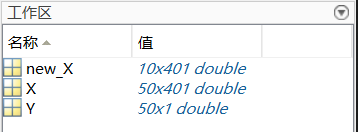打开APP选项卡中的Neural Net Fitting

弹出如下对话框,这个主要是模型的简介，：

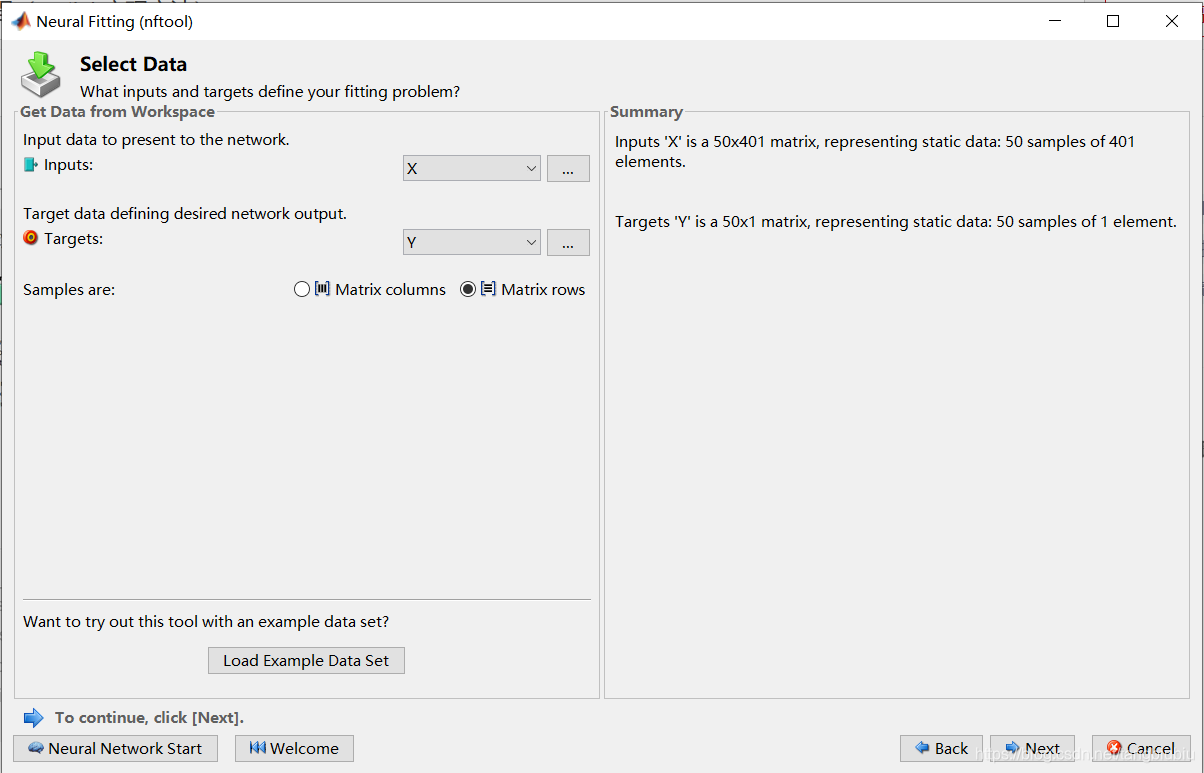
直接点NEXT得到下面对话框。Input选择输入值，Targets选择目标值。注意我们的数据是按行排列的，Samples选择Matrix rows。然后Next。

这个是训练集、验证集和测试集的比例，一般默认就好。Next。

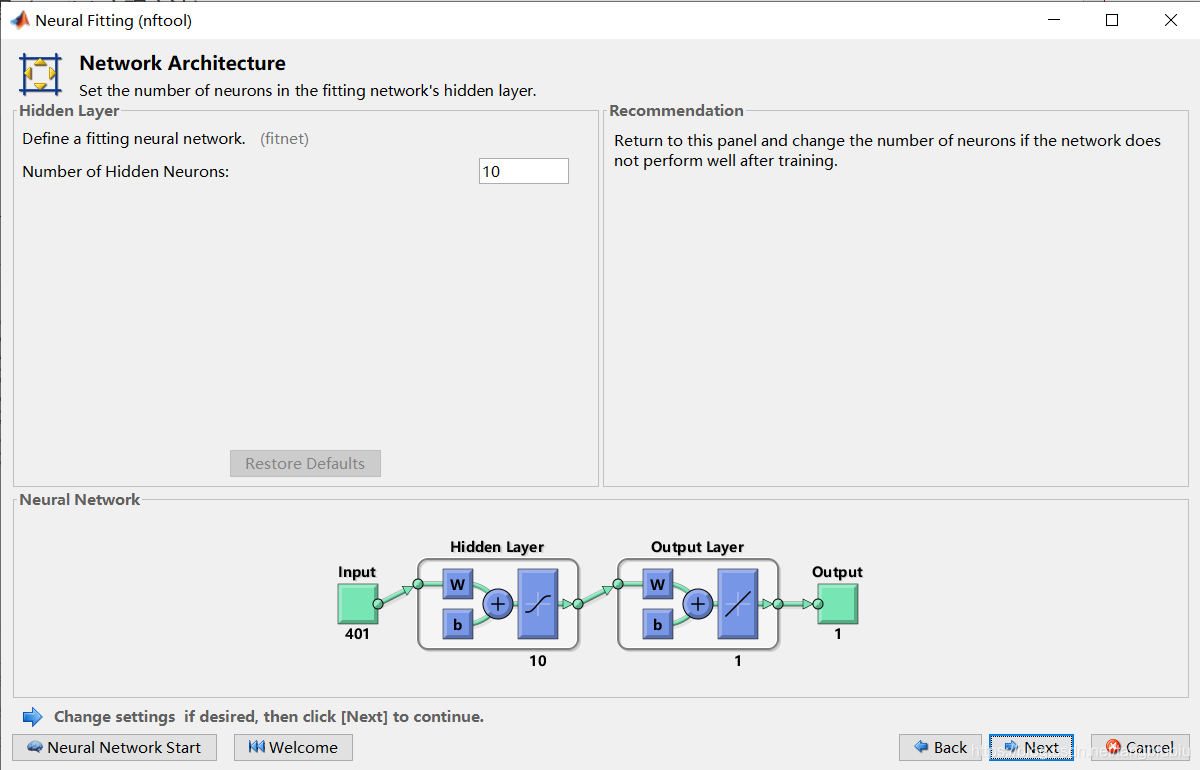
下面设定隐藏层神经元的个数，我选择默认，10。Next。

在下图的那个下拉框中选择算法。具体算法的区别可以百度一下。第二种是效果最好的，能有效减少过拟合现象，但收敛速度极慢。1、3两种算法不够准确，但很快。点击Train开始训练你的模型。
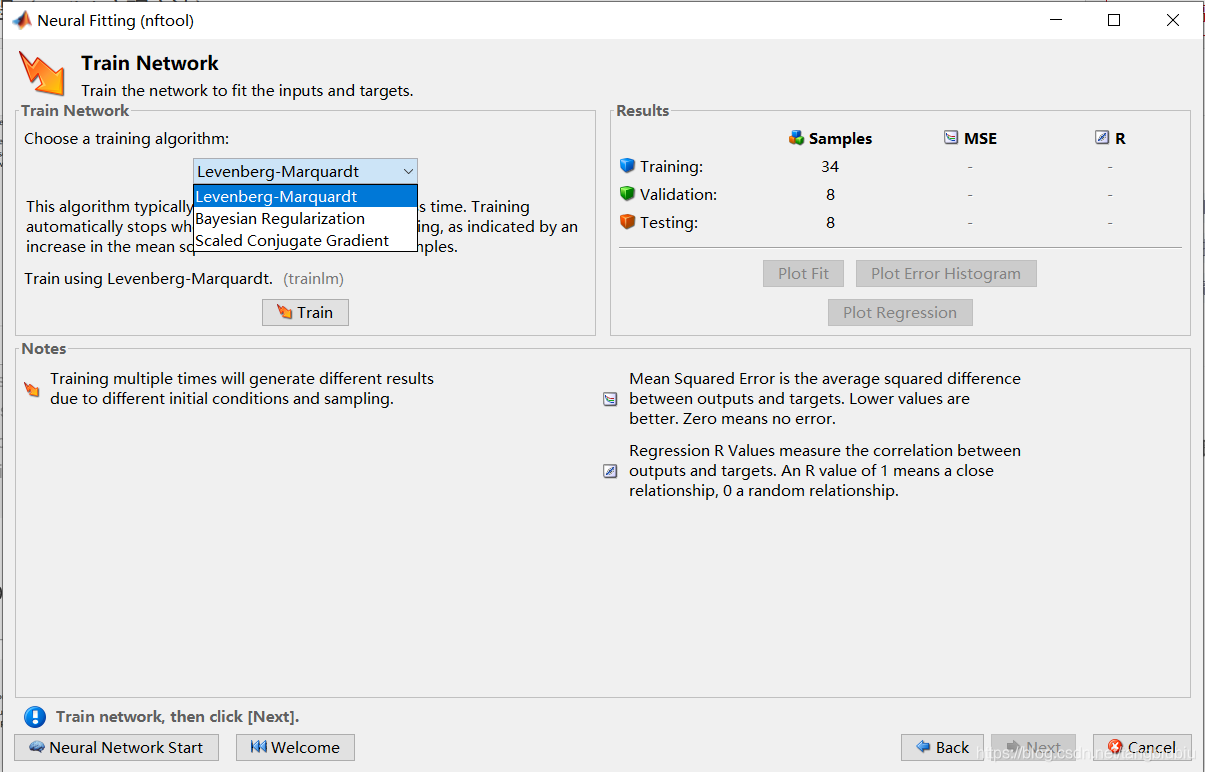弹出如下对话框：
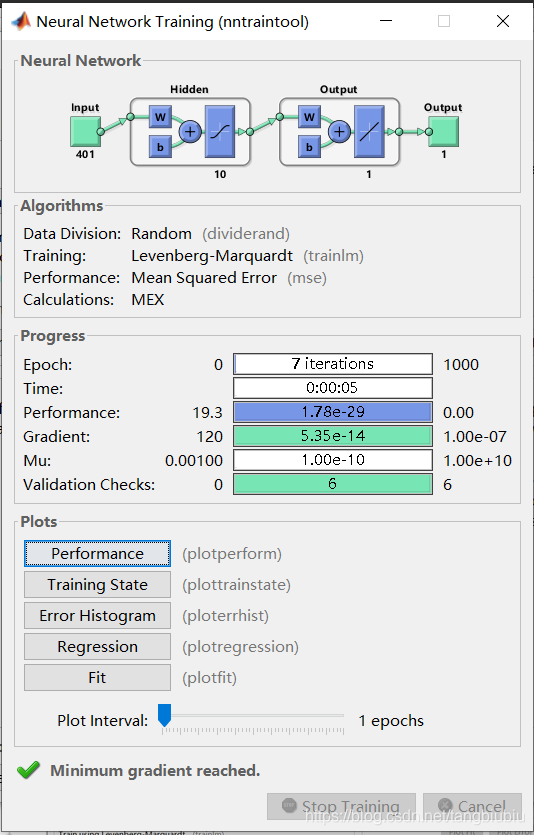点击Performance查看误差曲线，误差当然是越小越好。

点Fit查看三个集的回归图，R越接近1越好。
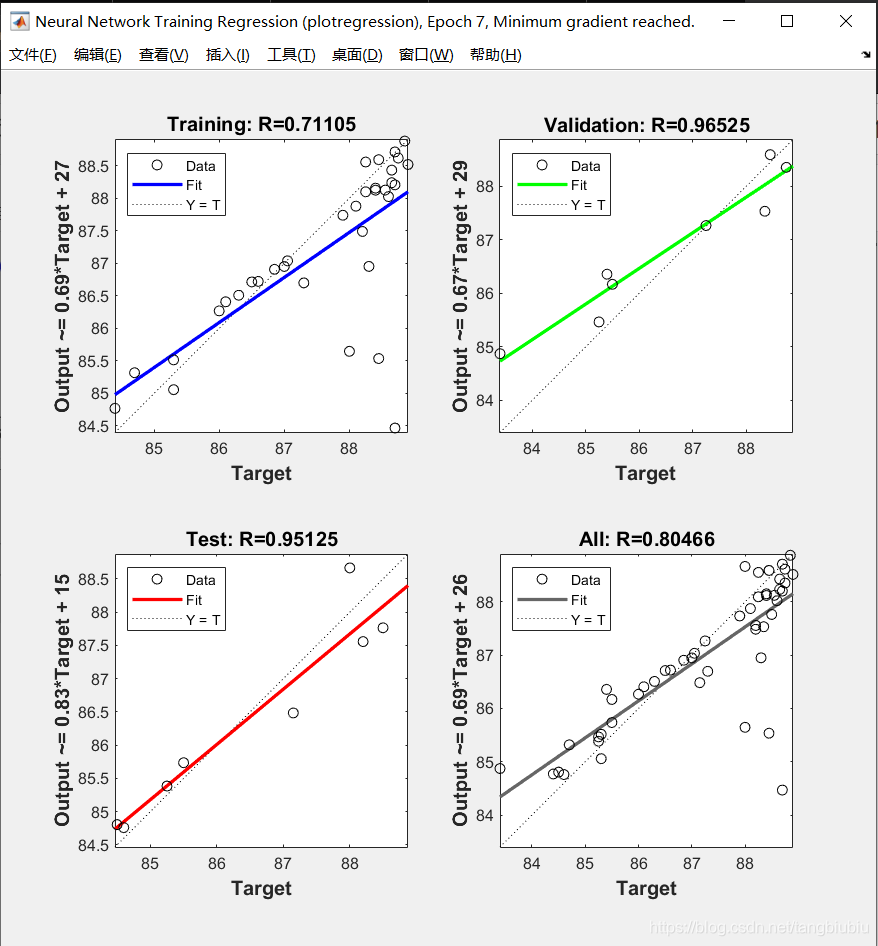回到下面这个页面，直接Next两次。

matlab Function是生成模型的matlab代码
Neural Network Diagram是模型示意图，放在论文里比较好看。Next。
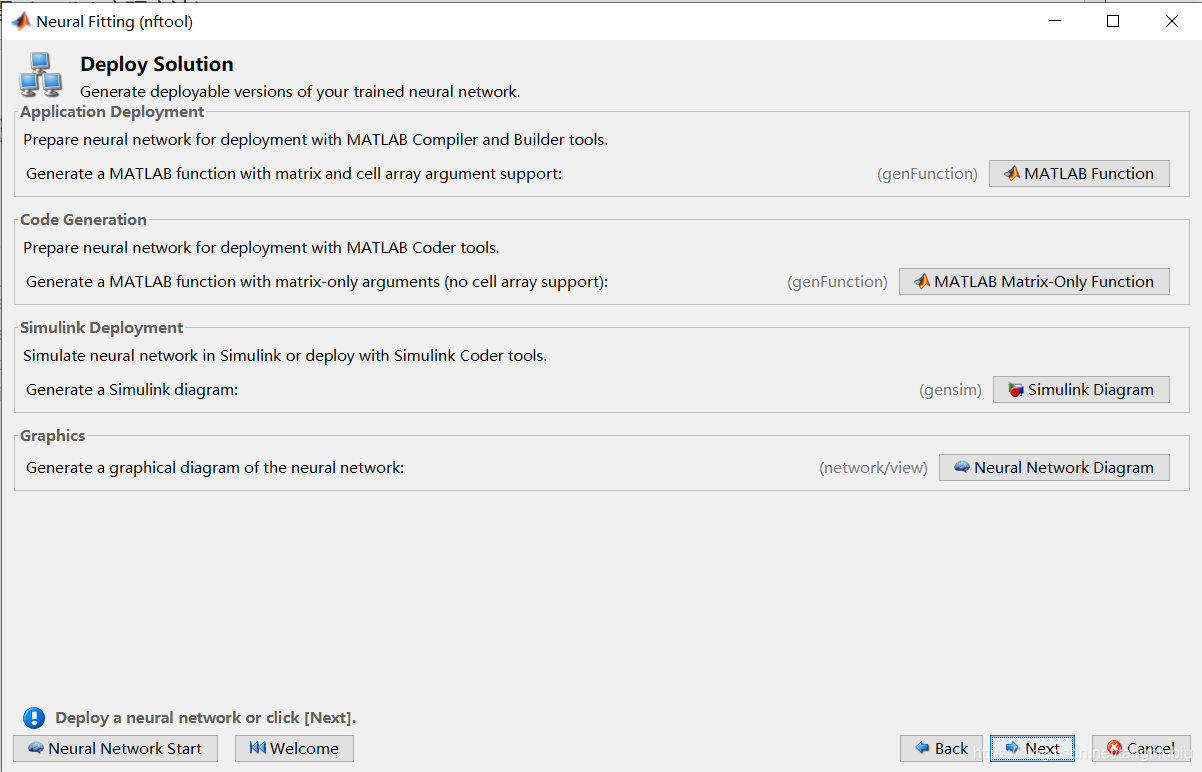点Save Results,然后Finsh。

模型就训练好了，下面可以做预测了，执行下面代码：

% 这里要注意，我们要将指标变为列向量，然后再用sim函数预测
sim(net, new_X(1,:)')

% 写一个循环，预测接下来的十个样本的辛烷值
predict_y = zeros(10,1); % 初始化predict_y
for i = 1: 10
    result = sim(net, new_X(i,:)');
    predict_y(i) = result;
end
disp('预测值为：')
disp(predict_y)
1
2
3
4
5
6
7
8
9
10
11

得到预测结果：

到这里，实现过程就成功了。

小伙伴，码字很辛苦的，如果你看懂了，请给我一个赞吧!