[人工智能-深度学习-8]：神经网络基础 - 机器学习、深度学习模型、模型训练_机器学习、深度神经网络、tr、大模型

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120462734

---

目录

第1章 白话机器学习

第2章 机器学习的模型与步骤

 2.1 深度学习与机器学习

2.2 机器学习的模型

第3章 建模

步骤1-1：研究问题领域的业务需求

步骤1-2：用于业务领域的数据进行测试

步骤1-3：模型部署

第4章 前向传播

步骤2-1：样本数据集（张量）

步骤2-2：数据预处理（张量运算）

步骤2-3：构建神经网络模型（nn）

步骤2-4：前向预测值（predict）

第5章 后向传播、后向求导（grad）

步骤3-1：loss损失函数（loss）

步骤3-2：优化器optimizer

步骤3-3：模型训练（机器学习、深度学习）

步骤3-4：模型验证（验证数据集）

第6章 模型导入

---

---

第1章 白话机器学习

[人工智能-综述-4]：白话深度学习-- 无基础小白都能理解机器学习的核心概念_文火冰糖（王文兵）的博客-CSDN博客

[人工智能-深度学习-7]：神经网络基础 - 人工神经网络ANN_文火冰糖（王文兵）的博客-CSDN博客

第2章 机器学习的模型与步骤

 2.1 深度学习与机器学习

上述三个概念中：人工智能的概念最广泛，所以有能机器具有类”人“一样智能的技术、非技术（如伦理）的领域，都是人工智能。

机器获取“智能”的一个重要手段是，机器具备“自我学习”的能力，所有能够使得机器具备自我学习能力的技术、算法都是机器学习。即通过为某一问题领域构建数学模型，并通过设计优化算法，让机器自动根据输入的样本数据，自动更新模型的参数，完成机器自动学习模型参数的过程。

深度学习是机器学习的一个特殊的领域和特殊的技术手段，它底层的模型预测模型是由大量的、简单的线性模型（y=wx+b)组合成的复杂的人工神经网络，通过设计模型优化算法，让机器根据输入的样本自动更新神经网络的基本的W,B参数，发现样本中被深度隐藏的规律，完成深度学习的过程。

 百度百科：机器学习是一门多学科交叉专业，涵盖概率论知识，统计学知识，近似理论知识和复杂算法知识，使用计算机作为工具并致力于真实实时的模拟人类学习方式，并将现有内容进行知识结构划分来有效提高学习效率。 [1]

机器学习有下面几种定义：

（1）机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能（最优化算法）。

（2）机器学习是对能通过经验（样本）自动改进（自动迭代模型参数）的计算机算法的研究。

（3）机器学习是用数据或以往的经验（输入样本），以此优化（最优化算法，更新模型参数）计算机程序的性能标准的研究。

百度百科：深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向，它被引入机器学习使其更接近于最初的目标——人工智能(AI, Artificial Intelligence)。 [1]

深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。 深度学习是一个复杂的机器学习算法，在语音和图像识别方面取得的效果，远远超过先前相关技术。

2.2 机器学习的模型

 在上述模型中，我们要阐述机器学习中的一些核心的概念和关键步骤和概念。

上图可分为四大部分：

1-x 分析业务领域的需求，建立模型

2-x 前向传播、前向计算

3-x 后向传播、后向计算

4-x 模型导入

第3章 建模

步骤1-1：研究问题领域的业务需求

工程技术人员首先研究业务领域的需求，并根据特殊的业务领域（图形、视觉、自然语言处理等）需求，建立上述模型，包括上图中的所有功能模块，剩下的就是机器自己、自动完成了。

步骤1-2：用于业务领域的数据进行测试

步骤1-3：模型部署

• 把模型部署，作为后台处理程序，部署到特定的业务领域的程序中
• 为特定的业务领域提供服务。

第4章 前向传播

步骤2-1：样本数据集（张量）

样本对于机器而言，就是经验数据，它是机器学习的输入。

机器通过学习数据集数据，发现数据集中的规律和特征，并根据数据集的特征，修正自己的模型参数（W,B)。

根据数据集的用途，把数据集分为：

• 训练数据集：用于模型训练的数据集
• 验证数据集：用于验证模型是否达标的数据集
• 测试数据集：对训练好的模型进行测试的数据集

数据集是通过张量Tensor的形式提供给神经网络的。

步骤2-2：数据预处理（张量运算）

在模型训练之前，需要多数据进行预处理（包括数据清洗），以使之符号模型的需要。

大量的张量运算

步骤2-3：构建神经网络模型（nn）

不同的业务系统，所需要的神经网络的模型是不同的，不同的深度学习的框架，神经网络的构建方法也是不相同的。就是构建相应的神经网络的模型，并用于对输入数据进行预测。

步骤2-4：前向预测值（predict）

根据当前模型的参数（可能是训练前或训练中或训练后的参数）进行预测，获得的输出。

• 不同的输入数据Xi，有不同的预测输出Yi_pred。
• 不同的业务领域，有不同的输出，基本的三类输出有：线性回归输出、二分类输出、多分类输出。
• 不同类型的输出，其输出函数不同：无输出函数、sigmod、softmax等。

第5章 后向传播、后向求导（grad）

步骤3-1：loss损失函数（loss）

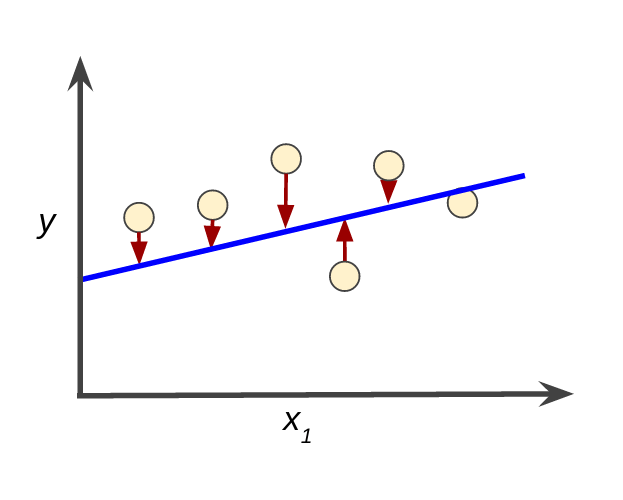
损失函数（loss function）或代价函数（cost function）。

它是用数学的方法，评估用当前模型参数进行前向推导/传播得到的预测值与样本的标签值之间的距离差或相似程度的函数。

不同的应用场合，其损失函数形式是不完全相同的！

其核心要义就是: 用一个函数来标识，所有样本点上的预测值与标签值的距离或误差和。

常见的损失函数有：

（1）0-1损失函数(zero-one loss)

0-1损失是指预测值和目标值（标签值）不相等为1， 否则为0，来表达他们之间的距离。

（2）绝对值损失函数

绝对值损失函数是计算预测值与目标值的差的绝对值来表达他们之间的距离。

 用|Yi-Yi_pred|绝对值来表示预测点(Xi, Yi_pred）与样本点（Xi,Yi)的距离或误差/偏差。

（3）平方损失函数

平方损失损失函数是计算预测值与目标值的差的平方来表达他们之间的距离。

 用(Yi-Yi_pred)^2来表示预测点(Xi, Yi_pred）与样本点（Xi,Yi)的距离或误差/偏差。

（4）直接用预测值标识距离

当输出值在0-1之间，标签值为0或1时，可以直接用输出值p或1-p直接表示距离。

（5）log对数损失函数

当输出值和标签值的差在[0,1]之间，为了放大相邻点的距离，可以通过log函数表示他们的距离。

 很显然，经过对数处理后，在[0,1]的数据，被放大到[0,+无穷]

（5）指数损失函数（exponential loss）

 用指数的形式表示损失损失。

（6）交叉熵损失函数 (Cross-entropy loss function)

交叉熵是用预测值+log组合而成，来标识损失值的方法。

这个概念理解起来比较困境，后续在进一步探讨。

步骤3-2：优化器optimizer

如果说，loss函数，通过数学函数的方式，表达了通过当前的模型参数获得的数据集上的所有预测值与数据集上的所有标签值的误差的和。

那么优化器，就是定义某种算法，通过自动调整模型的参数，使得模型的预测值（输出值）与样本值之间的误差和是最小的，就求loss函数的最小值数值方法（计算机求极小值的算法）。

（1）一元函数的loss函数 （只有一个W参数）

 （2）多元函数的loss函数（多个W，B参数 ）

（3）常见的优化器算法：

• 梯度下降法(Gradient Descent)

梯度下降法是最基本的一类优化器，是当今最流行的优化（optimization）算法，亦是至今最常用的优化神经网络的方法。

基本策略可以理解为”在有限视距内寻找最快路径下山“，因此每走一步，参考当前位置最陡的方向(即梯度)进而迈出下一步。可以形象的表示为：

目前主要分为三种同源的梯度下降法，他们之前的区别在于一次迭代所需要的样本的数量

标准梯度下降法(GD, Gradient Descent)：每次迭代计算，使用所有的样本。

θ=θ−η⋅∇θJ(θ)
每迭代一步，都要用到训练集的所有数据，每次计算出来的梯度求平均
η代表学习率LR

随机梯度下降法(SGD, Stochastic Gradient Descent)，每次迭代计算，使用有限个随机样本。

θ=θ−η⋅∇θJ(θ;x(i);y(i))
通过每个样本来迭代更新一次，以损失很小的一部分精确度和增加一定数量的迭代次数为代价，换取了总体的优化效率的提升。增加的迭代次数远远小于样本的数量。

批量梯度下降法(BGD, Batch Gradient Descent)，每次迭代，所有样本中的一组样本。

θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n))
为了避免SGD和标准梯度下降中存在的问题，对每个批次中的n个训练样本，这种方法只执行一次更新。【每次更新全部梯度的平均值】

带动量的梯度下降法

动量优化方法是在梯度下降法的基础上进行的改变，具有加速梯度下降的作用。

一般有标准动量优化方法Momentum、NAG（Nesterov accelerated gradient）动量优化方法。

Momentum是模拟物理里动量的概念，积累之前的梯度（称为动量）来替代真正的梯度，并作为当的梯度。即在正确梯度方向上加速，并且抑制波动方向张的波动大小，在后期本次计算出来的梯度会很小，以至于无法跳出局部极值，Momentum方法也可以帮助跳出局部极值。

Nesterov accelerated gradient (NAG)

 

 NAG方法收敛速度明显加快。波动也小了很多。

Adagrad：自适应梯度

前面的一系列优化算法有一个共同的特点，就是对于每一个参数都用相同的学习率进行更新。但是在实际应用中各个参数的重要性肯定是不一样的，所以我们对于不同的参数要动态的采取不同的学习率，让目标函数更快的收敛。
adagrad方法是将每一个参数的每一次迭代的梯度取平方累加再开方，用基础学习率除以这个数，来做学习率的动态更新。【这样每一个参数的学习率就与他们的梯度有关系了，那么每一个参数的学习率就不一样了！也就是所谓的自适应学习率】

Adagrad的一大优势时可以避免手动调节学习率，比如设置初始的缺省学习率为0.01，然后就不管它，另其在学习的过程中自己变化。当然它也有缺点，就是它计算时要在分母上计算梯度平方的和，由于所有的参数平方【上述公式推导中并没有写出来是梯度的平方，感觉应该是上文的公式推导忘了写】必为正数，这样就造成在训练的过程中，分母累积的和会越来越大。这样学习到后来的阶段，网络的更新能力会越来越弱，能学到的更多知识的能力也越来越弱，因为学习率会变得极其小【就会提前停止学习】，为了解决这样的问题又提出了Adadelta算法。

Adadelta

Adagrad会累加之前所有的梯度平方，而Adadelta只累加固定大小的项【其实就是相当于指数滑动平均，只用了前多少步的梯度平方平均值】，并且也不直接存储这些项，仅仅是近似计算对应的平均值【这也就是指数滑动平均的优点】

RMSprop

RMSProp算法的全称叫 Root Mean Square Prop，

在上面的Momentum优化算法中，虽然初步解决了优化中摆动幅度大的问题。所谓的摆动幅度就是在优化中经过更新之后参数的变化范围，如下图所示，蓝色的为Momentum优化算法所走的路线，绿色的为RMSProp优化算法所走的路线。 

为了进一步优化损失函数在更新中存在摆动幅度过大的问题，并且进一步加快函数的收敛速度，RMSProp算法对权重 W 和偏置 B 的梯度使用了微分平方加权平均数。 

Adam

Adam = Adaptive + Momentum，顾名思义Adam集成了SGD的一阶动量和RMSProp的二阶动量。

SGD可以使用类似于物理中的动量来累积梯度，RMSProp可以使得收敛速度更快同时使得波动的幅度更小。Adam把它们的优点结合起来，以取得的更好的表现效果。

不同优化算法的直观比较

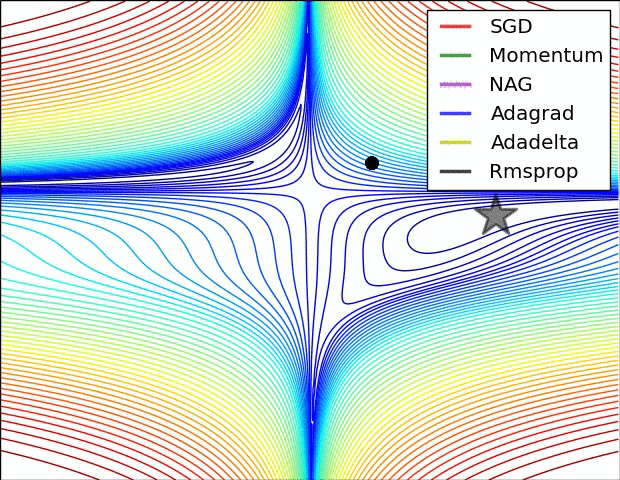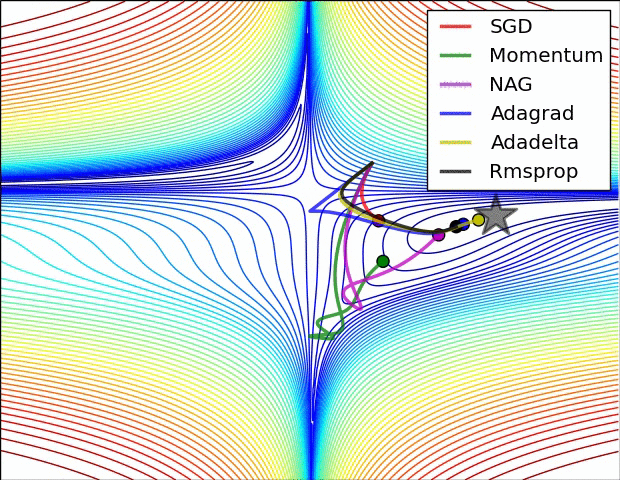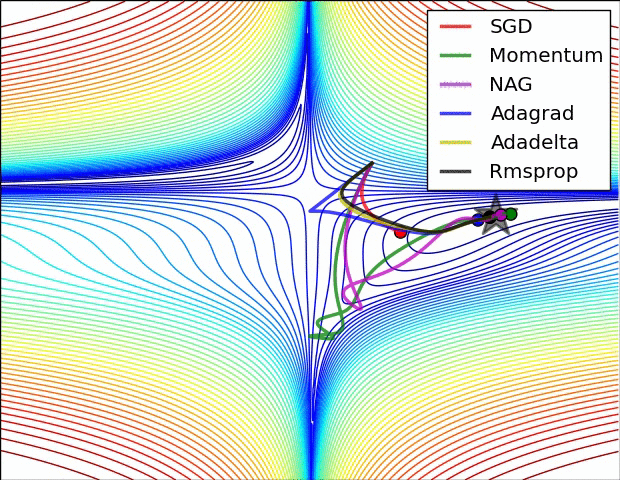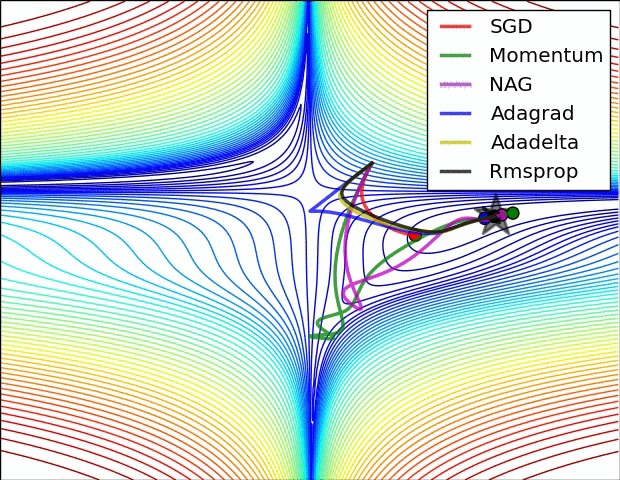
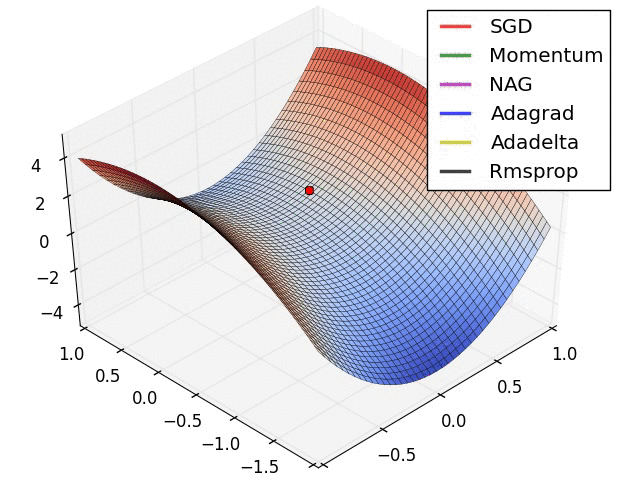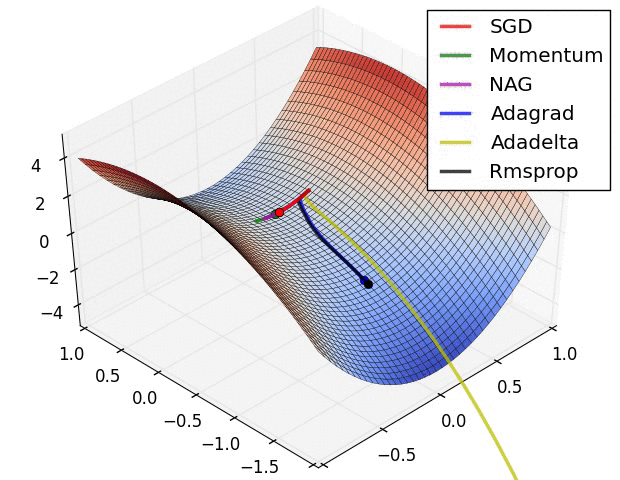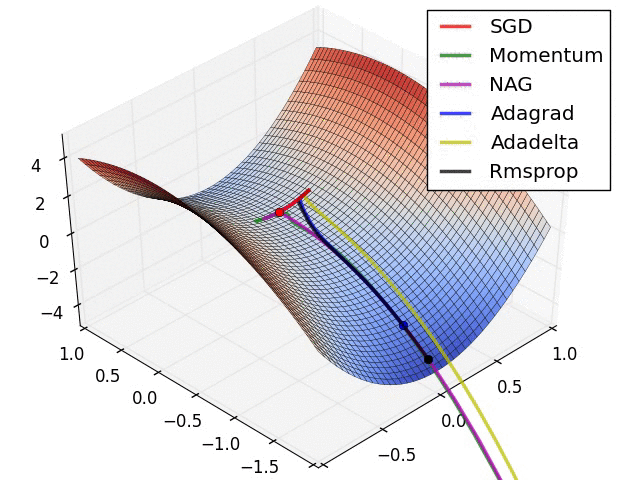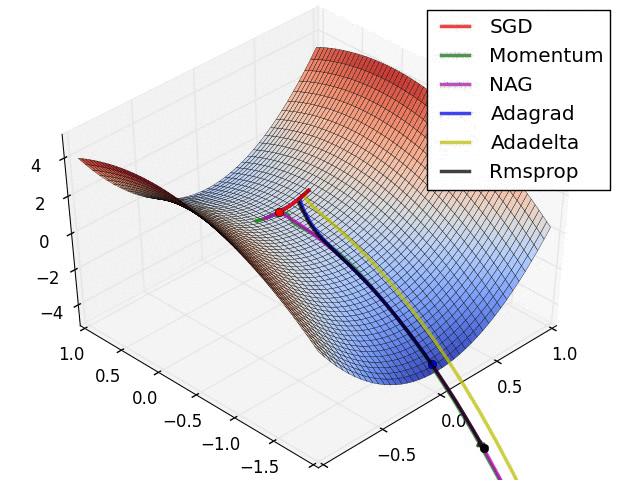
图 3 中，我们可以看到不同算法在损失面等高线图中的学习过程，它们均同同一点出发，但沿着不同路径达到最小值点。其中 Adagrad、Adadelta、RMSprop 从最开始就找到了正确的方向并快速收敛；SGD 找到了正确方向但收敛速度很慢；SGD-M 和 NAG 最初都偏离了航道，但也能最终纠正到正确方向，SGD-M 偏离的惯性比 NAG 更大。

图 4 展现了不同算法在鞍点处的表现。这里，SGD、SGD-M、NAG 都受到了鞍点的严重影响，尽管后两者最终还是逃离了鞍点；而 Adagrad、RMSprop、Adadelta 都很快找到了正确的方向。

不同算法，主要区别在于：

• 是否能够跳出极小值
• 收敛速度

提速又可以归纳为以下几个方面：
- 使用动量momentum来保持前进方向(velocity)；
- 为每一维参数设定不同的学习率：进；在梯度连续性强的方向上加速前
- 用历史迭代的平均值归一化学习率：突出稀有的梯度；

步骤3-3：模型训练（机器学习、深度学习）

优化算法，只给定了寻找loss函数最小值的方法，该方法还需要去实施，才能完成目标，实施涉及到：

（1）如何提供样本数据

（2）如何设定初始点

（3）如何设定初始学习率

（4）如何反复调用迭代算法进行反复迭代

（5）如何设定迭代收敛的条件

（6）如何记录迭代的中间过程

上述问题都是模型训练的职责。

步骤3-4：模型验证（验证数据集）

训练好的模型，需要对它进行验证，以确认模式是否已经得到预先设定的目标，这就是模型验证。

验证通过的模型从，才能为特定的业务进行服务。

验证不通过的模型，还需要进一步的训练和修正。

第6章 模型导入

训练模型需要花费大量的时间和算力，并非所有的模型参数，都需要自己亲自训练，也可以直接导入其他人训练好的模型。这就是模型的导入。

关于模型导入，后续单独探讨。

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120462734