C语言实现斐波那契数列的多种方法_斐波那契数列c语言

顾得泉：个人主页

个人专栏：《Linux操作系统》  《C/C++》  《LeedCode刷题》

键盘敲烂，年薪百万！

---

 斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo  Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。对于解决此类问题方法有四，前两种对于初学者来说，应该可以思考研究明白，后两种就要求有一点点基础了，但是我相信，大家都可以学会的！！！

一、递归方法

完整代码展示如下：​

#include <stdio.h>
 
int fib(int n) 
{
    if (n <= 1) 
    {
        return n;
    } 
    else 
    {
        return fib(n - 1) + fib(n - 2);
    }
}
 
int main() 
{
    int n;
    printf("请输入一个整数： ");
    scanf("%d", &n);
    printf("斐波那契数列第%d项为： %d", n, fib(n));
    return 0;
}

递归方法实现原理如下：

       首先检查输入的n是否小于等于1。如果是，那么直接返回n，因为斐波那契数列的前两项就是0和1。

       如果n大于1，那么函数会递归地调用自身两次，分别传入n-1和n-2作为参数。这是因为斐波那契数列的定义是每一项都是前两项的和。

       最后，将这两个递归调用的结果相加，并返回结果。

结果展示：

---

二、迭代方法

​完整代码展示如下：​

#include <stdio.h>
 
int fib(int n) 
{
    if (n <= 1) 
    {
        return n;
    }
    int a = 0, b = 1, temp;
    for (int i = 2; i <= n; i++) 
    {
        temp = a + b;
        a = b;
        b = temp;
    }
    return b;
}
 
int main() 
{
    int n;
    printf("请输入一个整数： ");
    scanf("%d", &n);
    printf("斐波那契数列的第%d项为： %d", n, fib(n));
    return 0;
}

 迭代方法实现原理如下：

       函数首先检查n是否小于等于1，如果是，则直接返回n。这是因为斐波那契数列的前两项是0和1。

       如果n大于1，函数使用一个循环来计算斐波那契数列的第n项。在每次迭代中，它计算a和b的和，并将结果存储在临时变量temp中。然后，它将b的值赋给a，将temp的值赋给b。这样，a和b分别表示斐波那契数列的前两项和当前项。

       循环继续进行，直到i等于n。最后，函数返回b的值，即斐波那契数列的第n项。

结果展示：

---

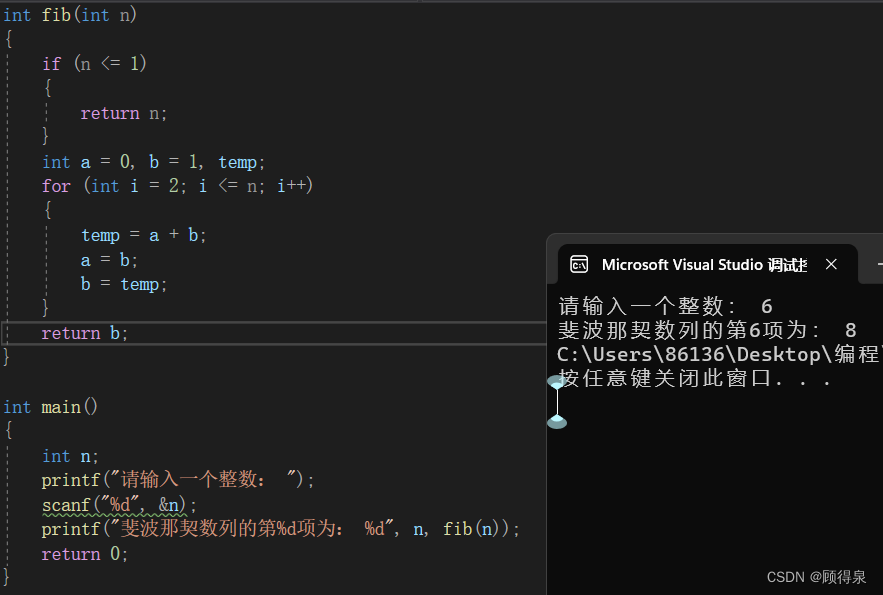
三、数组方法

​​完整代码展示如下：​

#include <stdio.h>
 
void fib(int n) 
{
    int a[n];
    a[0] = 0;
    a[1] = 1;
 
    for (int i = 2; i < n; i++) 
    {
        a[i] = a[i - 1] + a[i - 2];
    }
 
    for (int i = 0; i < n; i++) 
    {
        printf("%d ", a[i]);
    }
}
 
int main() 
{
    int n;
    printf("请输入斐波那契数列的长度： ");
    scanf("%d", &n);
    fib(n);
    return 0;
}

 数组方法原理如下：

       首先，代码声明了一个长度为n的整型数组a。然后，通过将数组的第一个元素和第二个元素分别赋值为0和1，初始化了斐波那契数列的前两个元素。

       接着，使用一个for循环从索引2开始迭代到n-1。在每次迭代中，代码计算斐波那契数列的第i个元素，即前两个元素的和，并将其存储在数组a的相应位置。

       最后，使用另一个for循环遍历数组a，并使用printf函数打印出每个元素的值。这样，你就可以看到斐波那契数列的前n个元素被打印出来了。

结果展示：

---

 四、通项公式方法

要实现斐波那契数列通项公式方法，我们首先需要了解斐波那契数列的通项公式：

        F(n) = (φ^n - (-φ)^-n) / sqrt(5)

        其中，φ = (1 + sqrt(5)) / 2。

​​​完整代码展示如下：​

#include <stdio.h>
#include <math.h>
 
double fibonacci(int n) 
{
    double phi = (1 + sqrt(5)) / 2;
    return (pow(phi, n) - pow(-phi, -n)) / sqrt(5);
}
 
int main() 
{
    int n;
    printf("请输入要计算的斐波那契数列项数：");
    scanf("%d", &n);
    printf("第%d项斐波那契数列值为：%lf", n, fibonacci(n));
    return 0;
}

通项公式方法原理如下：

       函数内部首先定义了一个变量phi，它的值为(1 + sqrt(5)) / 2，这是斐波那契数列中相邻两项之比的近似值。

       接着，函数使用公式(pow(phi, n) - pow(-phi, -n)) / sqrt(5)来计算斐波那契数列的第n项。其中，pow(x, y)表示求x的y次方，sqrt(x)表示求x的平方根。

       最后，函数返回计算得到的斐波那契数列第n项的值。

结果展示：

---

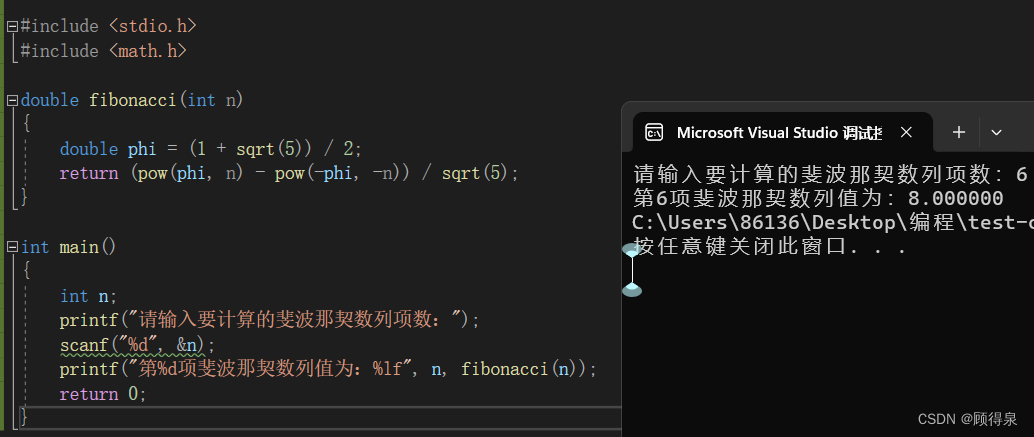
五、注意事项 

       第一种递归方法在计算较大的斐波那契数时可能会导致性能问题，因为它会重复计算许多相同的子问题。第三种方法使用了数组来存储已经计算过的斐波那契数列，可以提高效率。第四种方法使用了斐波那契数列的通项公式，可以直接计算出第n项的值，但是需要注意精度问题。

---

结语：以上就是相关斐波那契数列的解决方法了，希望对大家有所帮助。有什么问题欢迎大家留言~~~