递归、搜索与回溯算法（专题六：记忆化搜索）_记忆化回溯

目录

1. 什么是记忆化搜索（例子：斐波那契数）

1.1 解法一：递归

1.2 解法二：记忆化搜索

1.2.1 记忆化搜索比递归多了什么？

1.2.2 提出一个问题：什么时候要使用记忆化搜索呢？

1.3 解法三：动态规划

1.3.1 先复习一下动态规划的核心步骤（5个），并将动态规划的每一步对应记忆化搜索（加强版的递归）的每一步

1.3.2 通过上面的解析，发现一个特点

1.3.3 动态规划 and 记忆化搜索的本质 

补充

2. 题目

2.1  不同路径（medium）

2.1.1 递归解法

2.1.2 记忆化搜索解法

2.1.3 动态规划解法 

2.2 最长递增子序列

2.2.1 递归解法

2.2.2 记忆化搜索解法

2.2.3 动态规划解法 

2.3 猜数字大小 Ⅱ

2.3.1 递归解法

2.3.2 记忆化搜索解法

2.4 矩阵中的最长递增路径

2.4.1 递归解法

2.4.2 记忆化搜索解法

1. 什么是记忆化搜索（例子：斐波那契数）

力扣题目链接

记过前面几篇文章中，我介绍了什么递归、搜索和回溯，以及他们之间的关系。接下来我们进阶一下，来一起看看什么是记忆化搜索，看看记忆化搜索与递归，乃至动态规划算法之间有什么联系吧。

我打算用一道很经典的例题，分享一下什么是记忆化搜索，这道题就是斐波那契数！

斐波那契数的解法有很多（①循环；②递归；③动态规划；④记忆化搜索；⑤矩阵快速幂），在这几种解法中，矩阵快速幂的时间复杂度是最小的。

关于矩阵快速幂，我会在接下来的文章中分享给大家，敬请期待！！！

题目如下：

解法分析：

1.1 解法一：递归

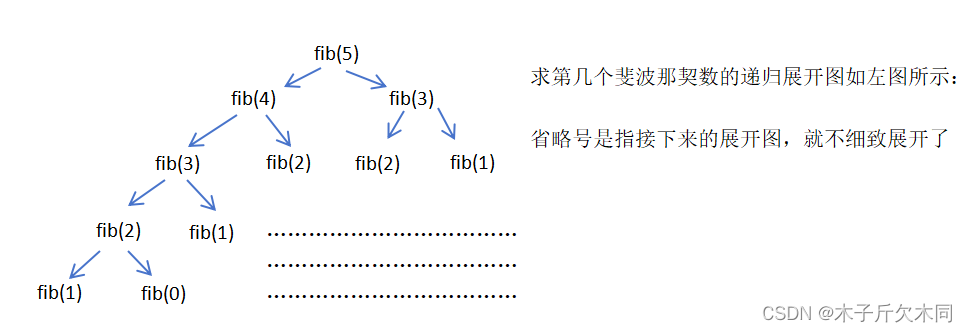
递归解决这题会出现的问题：

① 进行了很多重复性的计算，例如fib(3)、fib(2)都计算了多次，这就大大增加运算时间，时间复杂度为O(2^n)。

② 如果 n 太大，fib(n)的执行可能还会导致栈溢出。

    //第一种方法：递归
    public int fib1(int n) {
        if(n == 0) return 0;
        if(n == 1) return 1;
 
        return fib(n - 1) + fib(n - 2);
    }

​

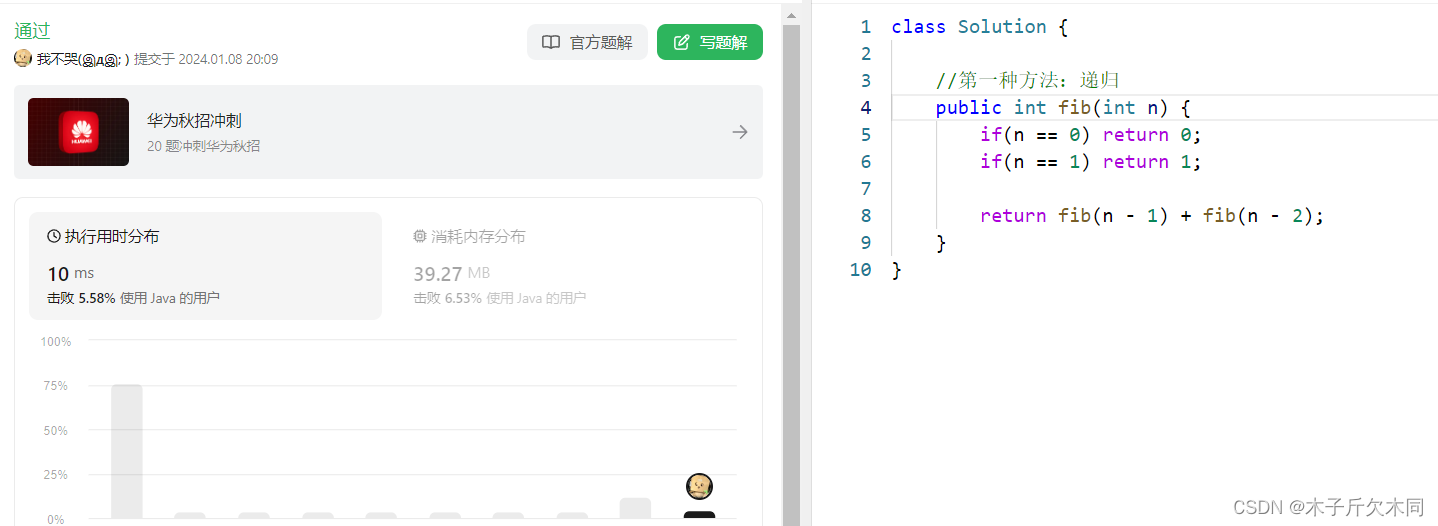
我们可以发现，递归是可以执行通过的。这道题给的测试用例都是比较少，所以不会导致超时的现象。

1.2 解法二：记忆化搜索

1.2.1 记忆化搜索比递归多了什么？

答：比递归多了一个“备忘录”的功能（加强版的递归）。在上面的第一种解法有提到递归的缺点就是有事会进行大量的重复计算，导致时间复杂度过大。“备忘录”就是用来存储每次递归的结果，如果在另一个分支中有进行一样的运算，就不需要再进行递归展开了，只要从“备忘录”中将值取出来直接返回即可。具体看下图：

首先我们创建一个备忘录，例如：int memo[n];

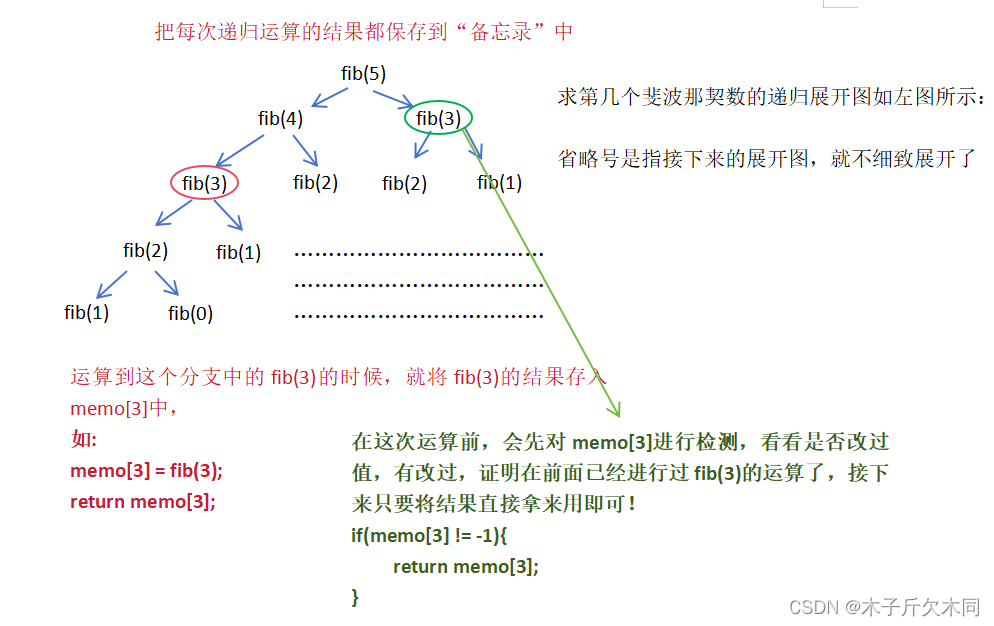
如何实现记忆化搜索？

① 添加一个备忘录。

② 递归每次返回时，将结果放到备忘录里面。

③ 在每次进入递归之前，先往备忘录里瞅一瞅，看看是否已经存在了 。

    int[] memo;//作为备忘录
    //第二种方法：记忆化搜索
    public int fib(int n) {
        //初始化
        memo = new int[n + 1];
        Arrays.fill(memo, -1);
        //进行记忆化深搜
        return dfs(n);
    }
 
    int dfs(int n){
        if(memo[n] != -1) return memo[n];
        if(n <= 1){
            memo[n] = n;
            return n;
        }
        memo[n] = dfs(n - 1) + dfs(n - 2);
        return memo[n];
    }

​

发现了一个有趣的结果，使用递归解这道题花了10ms，而使用记忆化搜索只要0ms！（虽然力扣的执行时间不是很严谨，但也可以一看） 

记忆化搜索，省略了很多重复计算的步骤，所以时间复杂度大大减少了，为 O(n)。

1.2.2 提出一个问题：什么时候要使用记忆化搜索呢？

答：① 只有当一个道题有许多重复计算，换句话说，有许多重复的子问题时，可以使用记忆化搜索来降低时间复杂度。② 如果没有许多重复计算，换句话说递归展开图只是一棵单分支树，就没必要用记忆化搜索了。

1.3 解法三：动态规划

1.3.1 先复习一下动态规划的核心步骤（5个），并将动态规划的每一步对应记忆化搜索（加强版的递归）的每一步

① 确定动态表示：dp[i]要表示什么，dp[i]表示第i位的斐波那契数 ——> 递归：dfs函数的含义（函数头有什么参数、什么返回值）

② 确定动态转移方程：dp[i] = dp[i - 1] + dp[i - 2] ——> 递归：dfs函数的主体（函数做了什么）

③ 初始化：防止越界，dp[0] = 0，dp[1] = 1 ——> 递归：dfs函数的递归出口（n == 0 或 n == 1时）

④ 确定填表顺序：从左往右 ——> 递归：填写备忘录的顺序

⑤ 确定返回值：dp[n] ——> 递归：主函数如何调用dfs函数
 

    int[] dp;
    public int fib(int n) {
        //1.对dp初始化
        dp = new int[n + 1];
        dp[0] = 0;
        if(n > 0)
            dp[1] = 1;
        //2.开始填表
        for(int i = 2;i <= n;i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        //3.返回值
        return dp[n];
    }

​

1.3.2 通过上面的解析，发现一个特点

记忆化搜索是进行自顶向下计算，动态规划是进行自底向上计算。

1.3.3 动态规划 and 记忆化搜索的本质 

① 都是暴力解法，一一枚举

② 都是将计算好的结果存储起来

③ 记忆化搜索（递归的形式），动态规划（递推的形式，利用循环）

补充

（1）带备忘录的递归 vs 带备忘录的动态规划 vs 记忆化搜索 三者都是一回事，就是记忆化搜索或者说动态规划。

（2）能用暴搜解的题，一般可以改成记忆化搜索，但不一定可以改成动态规划。暴搜的本质是给动态规划提供一个“填表方向”。

经过上面的分享，大家应该对递归、记忆化搜索和动态规划有了一个新的了解，接下来通过做题来巩固加深我们的知识体系吧。

2. 题目

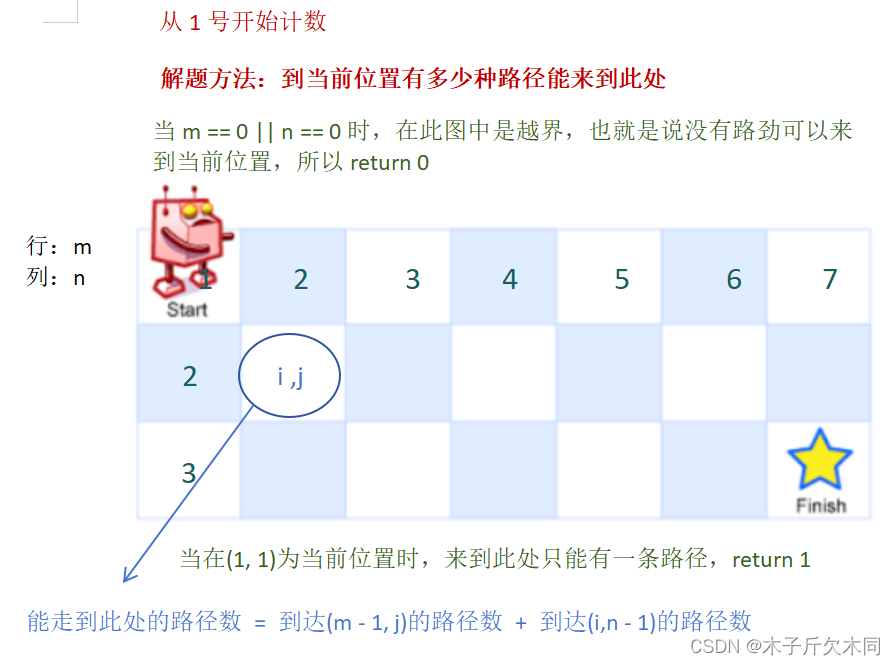
2.1  不同路径（medium）

力扣题目链接

 解析：

2.1.1 递归解法

    //第一种：递归解法
    public int uniquePaths(int m, int n) {
        if(m == 0 || n == 0) return 0;
        if(m == 1 && n == 1) return 1;
        return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
    }

 在运行的时候是可以运行通过，但是当 m 和 n 太大了呢？我们来看看提交会发生什么。

超时！！！ m和n一大就发什么超时现象，接下来看看用记忆化搜索又怎么样。

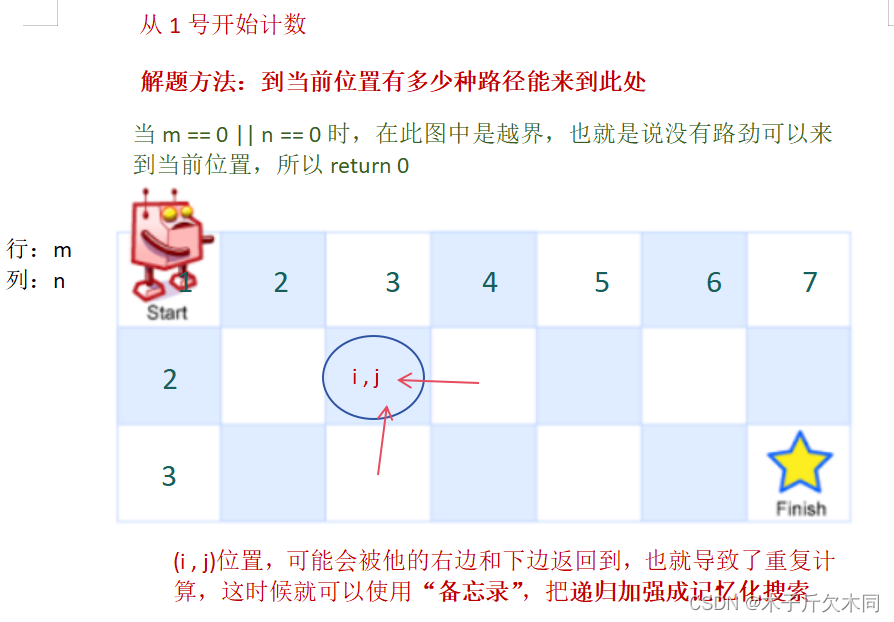
2.1.2 记忆化搜索解法

    //第二种：记忆化搜索
    public int uniquePaths(int m, int n) {
        int[][] memo = new int[m + 1][n + 1];
        return dfs(m,n,memo);
    }
    int dfs(int m,int n,int[][] memo) {
        if(m == 0 || n == 0) return 0;
        if(memo[m][n] != 0) return memo[m][n];
        if(m == 1 && n == 1){
            memo[m][n] = 1;
            return 1;
        }
        memo[m][n] = dfs(m-1,n,memo) + dfs(m,n-1,memo);
        return memo[m][n];
    }

此时提交就可以通过了，不会发生超时。

2.1.3 动态规划解法 

（1）确定动态表示：dp[i][j] 为 到当前位置有多少种路径。

（2）状态转移方程：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

（3）初始化：dp[0][j] = dp[i][0] = 0，dp[1][1] = 1。

（4）填表顺序：从左往右，从上往下。

（5）返回值：return dp[m][n]。

    // 第三种：动态规划解法
    public int uniquePaths(int m, int n) {
        //1.创建dp表
        int[][] dp = new int[m + 1][n + 1];
        //2和3一起，初始化和填表
        dp[1][1] = 1;
        for(int i = 1;i < m + 1;i++){
            for(int j = 1;j < n + 1;j++){
                if(i == 1 && j == 1) continue;//到(1,1)位置的路径都是1，不用再修改了
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        //4.返回值
        return dp[m][n];
    }

​

2.2 最长递增子序列

力扣题目链接

 解析：

2.2.1 递归解法

    public int lengthOfLIS(int[] nums){
        int ret = 0;
        for(int i = 0;i < nums.length;i++){
            ret = Math.max(ret,dfs(nums,i));
        }
        return ret;
    }
    public int dfs(int[] nums,int pos){
        int ret = 1;
        for(int i = pos + 1;i < nums.length;i++){
            if(nums[pos] < nums[i])
                ret = Math.max(ret,dfs(nums,i) + 1);
        }
        return ret;
    }

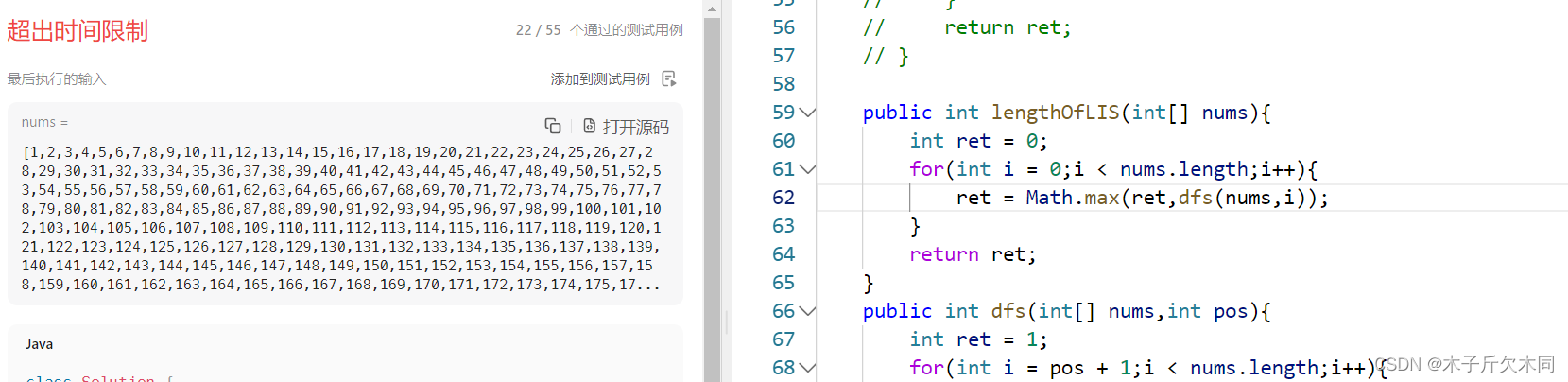
我们可以发现一些测试用例是可以通过，但是当数组的大小过于大时，就会报超时的错误！！！

对于这种情况，可以将代码改成记忆化搜索或者动态规划，用空间换取时间，减小时间复杂度！！！

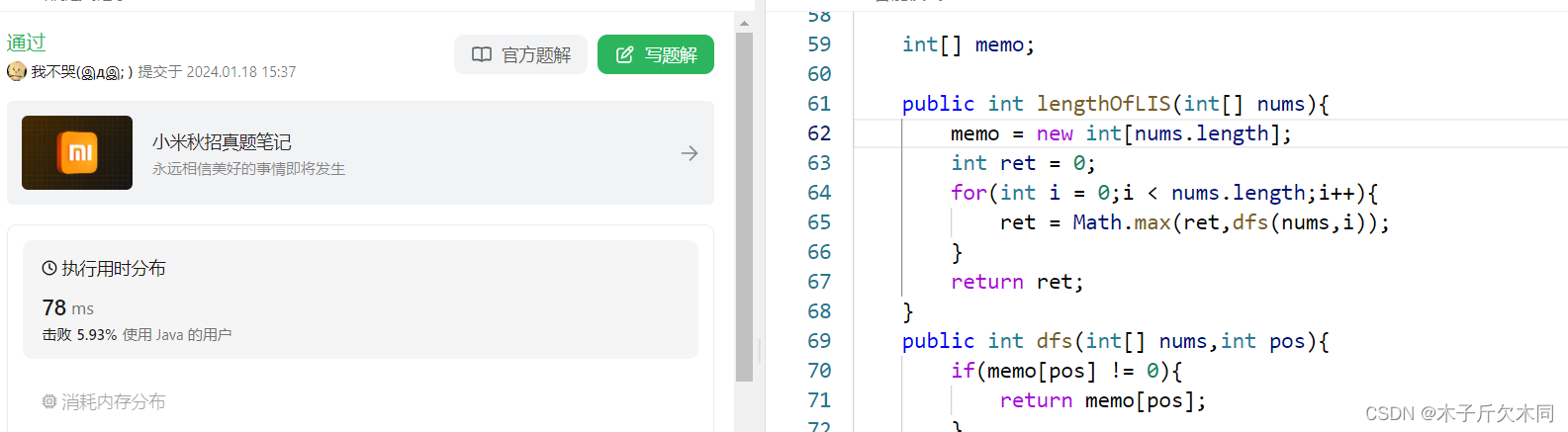
2.2.2 记忆化搜索解法

例如这种情况：在pos的第一个分支，pos+1已经计算过了，则在根结点的第二个分支就不需要在此重复计算pos+1了。

    int[] memo;
 
    public int lengthOfLIS(int[] nums){
        memo = new int[nums.length];
        int ret = 0;
        for(int i = 0;i < nums.length;i++){
            ret = Math.max(ret,dfs(nums,i));
        }
        return ret;
    }
    public int dfs(int[] nums,int pos){
        if(memo[pos] != 0){
            return memo[pos];
        }
        int ret = 1;
        for(int i = pos + 1;i < nums.length;i++){
            if(nums[pos] < nums[i])
                ret = Math.max(ret,dfs(nums,i) + 1);
        }
        memo[pos] = ret;
        return ret;
    }

2.2.3 动态规划解法 

（1）确定动态表示：dp[i] 表示从第i个位置开始，符合子序列条件的子序列长度为多少

（2）状态转移方程：当后一个元素大于前一个元素，有 dp[i] = Math.max(dp[i],dp[j] + 1); 

（3）初始化：Arrays.fill(dp,1); 所有的位置都是1，最糟糕的情况就是该位置的元素自己，所以就是1。

（4）填表顺序：从右往左。其实就是从少到多的过程。

（5）返回值：ret = Math.max(dp[i],ret); 看从哪个位置开始，能得到最长的子序列。

    //第三种：动态规划
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length + 1];
        int ret = 0;
        Arrays.fill(dp,1);
        for(int i = nums.length - 1;i >= 0;i--){
            for(int j = i + 1;j < nums.length;j++){
                if(nums[i] < nums[j]){
                    dp[i] = Math.max(dp[i],dp[j] + 1);
                }
            }
            ret = Math.max(dp[i],ret);
        }
        return ret;
    }

2.3 猜数字大小 Ⅱ

力扣题目链接

解析：

2.3.1 递归解法

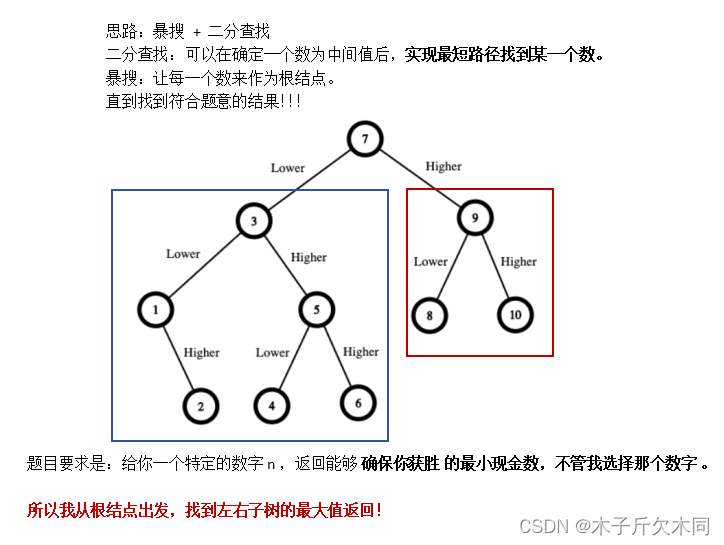
    //第一种方法：暴搜
    public int getMoneyAmount(int n) {
        return dfs1(1,n);
    }
    int dfs1(int left,int right){
        /*
        当left == right证明已经找到该数，所以就不需要支付费用
        当1作为根结点，则有 [left,head - 1] == [1,0]，这种情况不存在也
        要返回0，因为不存在，所以不会有消耗
        */
        if(left >= right) return 0;
        int ret = Integer.MAX_VALUE;
        for(int head = left;head <= right;head++){
            //x是用来找左子树的值
            int x = dfs1(left,head - 1);
            //y是用来找右子树的值
            int y = dfs1(head + 1,right);
            ret = Math.min(Math.max(x,y)+head,ret);
        }
        return ret;
    }

 这种超时报错，我们在上面的例题中已经遇到了许多次，所以我们将代码改为记忆化搜索

2.3.2 记忆化搜索解法

可以发现在选择5作为根结点时，出现了[6, 10]的区间；在选择3作为根结点时，也出现了[6, 10]的区间，这部分就导致了重复计算。所以我们将每个区间的结果保存起来，减少时间复杂度。

    //第二种方法：记忆化搜索
    int[][] memo;
    public int getMoneyAmount(int n) {
        memo = new int[n + 1][n + 1];
        return dfs(1,n);
    }
    int dfs(int left,int right){
        if(left >= right) return 0;
 
        if(memo[left][right] != 0) return memo[left][right];
        
        int ret = Integer.MAX_VALUE;
        for(int head = left;head <= right;head++){
            int x = dfs(left,head - 1);
            int y = dfs(head + 1,right);
            ret = Math.min(Math.max(x,y)+head,ret);
        }
        memo[left][right] = ret;
        return ret;
    }

2.4 矩阵中的最长递增路径

力扣题目链接

 解析：

2.4.1 递归解法

算法思路：暴搜
a. 递归含义：给 dfs ⼀个使命，给他⼀个下标 [i, j] ，返回从这个位置开始的最⻓递增路径
的⻓度；
b. 函数体：上下左右四个⽅向瞅⼀瞅，哪⾥能过去就过去，统计四个⽅向上的最⼤⻓度；
c. 递归出⼝：因为我们是先判断再进⼊递归，因此没有出⼝~

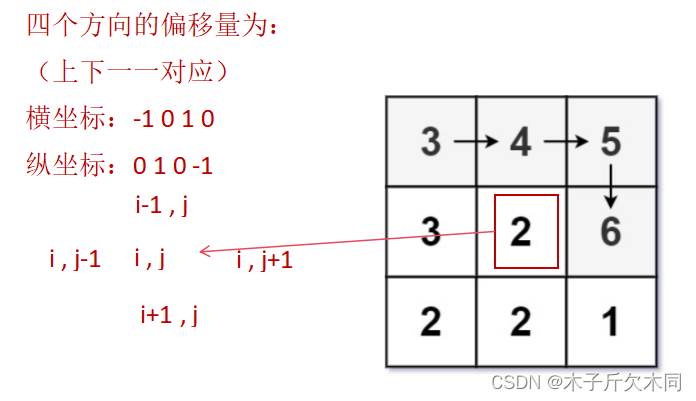
    //方向的选择：具体看上图
    int[] dx = {-1,0,1,0};
    int[] dy = {0,1,0,-1};
    int m,n;
    public int longestIncreasingPath(int[][] matrix) {
        m = matrix.length;
        n = matrix[0].length;
        int ret = 0;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                ret = Math.max(ret,dfs(matrix,i,j));
            }
        }
        return ret;
    }
    public int dfs(int[][] matrix,int i,int j){
        int ret = 1;
        //从四个方向进行暴搜
        for(int k = 0;k < 4;k++){
            int x = i + dx[k],y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y]
            > matrix[i][j]){
                ret = Math.max(ret,dfs(matrix,x,y) + 1);
            }
        }
        return ret;
    }

 这种超时报错，我们在上面的例题中已经遇到了许多次，所以我们将代码改为记忆化搜索。

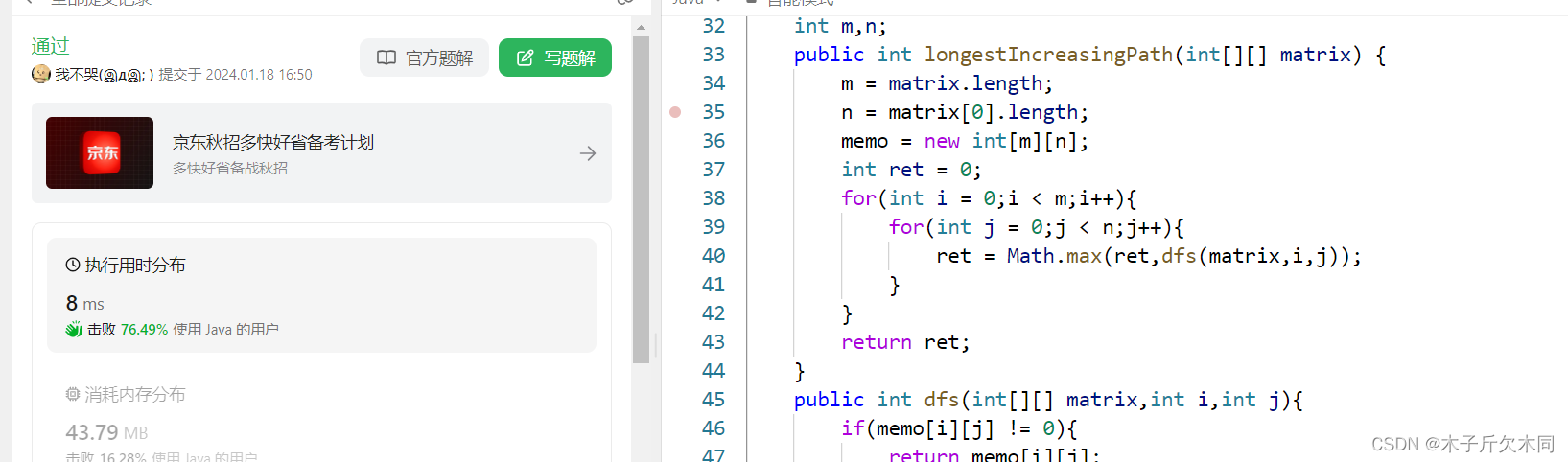
2.4.2 记忆化搜索解法

注：这道题的递归图为什么会重复就不给小伙伴们画了，大家可以动手画一画，想想为什么会有重复计算？

int[] dx = {-1,0,1,0};
    int[] dy = {0,1,0,-1};
    int[][] memo;//“备忘录”
    int m,n;
    public int longestIncreasingPath(int[][] matrix) {
        m = matrix.length;
        n = matrix[0].length;
        memo = new int[m][n];
        int ret = 0;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                ret = Math.max(ret,dfs(matrix,i,j));
            }
        }
        return ret;
    }
    public int dfs(int[][] matrix,int i,int j){
        if(memo[i][j] != 0){
            return memo[i][j];
        }
 
        int ret = 1;
        for(int k = 0;k < 4;k++){
            int x = i + dx[k],y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y]
            > matrix[i][j]){
                ret = Math.max(ret,dfs(matrix,x,y) + 1);
            }
        }
        memo[i][j] = ret;//每次结果保存到备忘录
        return ret;
    }