谈多重共线性

谈多重共线性

本文主要讨论古典假定中无多重共线性被违反的情况，主要情况包括多重共线性的实质和产生的原因、后果、检验方法及无多重共线性假定违反后的处置方法。

第一节 什么是多重共线性

一、多重共线性的含义

讨论多元线性回归模型的估计时，强调了假定无多重共线性，即假定各解释变量之间不存在线性关系，或者说各解释变量的观测值之间线性无关。计量经济学中的多重共线性，不仅包括解释变量之间精确的线性关系，还包括解释变量之间近似的线性关系。
从数学意义上去说明多重共线性，即若存在不全为0的数使得：

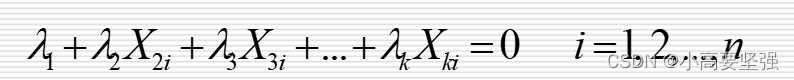
则称解释变量X1，X2，X3，…，Xk之间存在完全的多重共线性。

用矩阵来表示的话，解释变量的数据矩阵的秩<k，即解释变量的个数，表明在数据矩阵X中，至少有一个列向量可以用其余的列向量线性表示，说明存在完全的多重共线性。

在实际经济问题中，完全的多重共线性并不多见。常见的情形是解释变量X1、X2，…，Xk之间存在不完全的多重共线性。不完全的多重共线性是指对于解释变量X1，X2，…,Xk，存在不全为0的数，使得

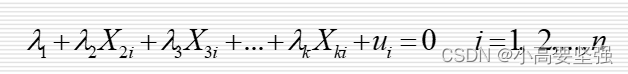
式中，ui为随机变量。这表示解释变量之间只是一种近似的线性关系。

如果解释变量之间不存在完全或不完全的线性关系，则称无多重共线性。需要强调，解释变量之间不存在线性关系，并非不存在非线性关系，当解释变量存在非线性关系时，并不违反无多重共线性假定。

回归模型中解释变量的关系可能表现为以下三种情形。
（1）r(xi,xj)=0，解释变量间毫无线性关系，变量间相互正交。事实上这是已经不需要做多元回归，每个参数Bj都可以通过y对xj的一元回归来估计。
（2）r(xi,xj)=1，解释变量间完全共线性。此时模型参数将无法确定。直观地看，当两变量按同一方式变化时，要区别每个解释变量对被解释变量的影响程度非常困难。
（3）0<r(xi,xj)<1，解释变量间存在一定程度的线性关系。实际中常遇到的是这种情形。

共线性程度的增加，会对参数估计值的准确性、稳定性带来影响。因此，不完全的多重共线性事实上有严重程度的问题。

二、产生多重共线性的背景

由于经济现象的变化涉及多个影响因素，而影响因素之间常常存在一定的相关性，多重共线性产生的经济背景主要有以下几种情形。

（1）经济变量之间具有共同变化趋势。例如，时间序列数据收入、消费等，在经济上升时，均出现增长的趋势，相反，在经济衰退期，又都出现下降趋势。当这些变量作为解释变量引入模型中会带来多重共线性问题。

（2）模型中包含滞后变量。当建立的模型中引入解释变量的滞后变量时，而X变量与滞后期变量常常高度相关，于是导致出现多重共线性。

（3）利用截面数据建立模型也可能出现多重共线性。利用截面数据建模时，许多变量与发展规模相关，会呈现出共同增长的趋势，如资本、劳动力、科技等投入与产出的规模相关，这时容易导致多重共线性。有时，如果出现部分因素变化与另一部分因素的变化相关程度较高，也容易出现共线性。

（4）样本数据自身的原因。例如，抽样仅仅限于总体中解释变量取值的一个有限的范围，使得变量变异不大；或由于总体有限，多个解释变量的样本数据之间相关，这时都可能出现多重共线性。

第二节 多重共线性产生的后果

一、完全多重共线性产生的后果

1. 参数的估计值不确定

完全共线性时，X矩阵的秩小于k，所以根据线性代数知识，正规方程组的解不唯一，回归参数的最小二乘估计表达式不成立。

从OLS估计来看，可以证明：

这说明当两个变量之间存在完全多重共线性时，参数的估计值是不确定的。

从回归模型的建模思想看，在回归模型中回归系数B2估计的含义是指在X3（以二元线性回归为例）不变的情况下，当X2每变动一个单位时Y的平均变化；回归系数B3估计的含义是指保持X2不变的情况下，当X3每改变一个单位时Y的平均变化。如果X2和X3完全共线性，就没有办法能在保持X2不变的情况下，分析X3对Y的影响。或者说，没有办法能从所给的样本中把X2和X3各自的影响分解开来。

2、参数估计值的方差无限大

OLS估计式的方差称为无穷大。即：

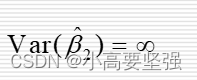
这表明，在解释变量存在完全多重共线性时，参数估计值的方差将变成无限大。

二、不完全多重共线性产生的后果

通常，解释变量之间并不一定是完全的线性关系。如果模型中存在不完全的多重共线性，是可以得到参数的估计值的，但是对计量分析可能会产生一系列的影响。

（1）参数估计值的方差与协方差增大。

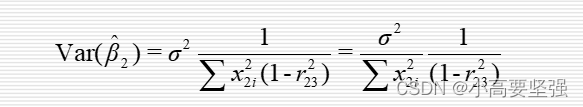
当r23趋于1时，参数估计量的方差也将增大。同样其协方差也在绝对值上也增大。可以看出，方差和协方差增大的速度取决于方差扩大因子。将VIF定义为1/(1-r23平方)

VIF表明，参数估计量的方差是由于多重共线性的出现而膨胀起来的。随着共线性的增加，参数估计量的方差也增大，当r23平方趋于1时，甚至可以变至无穷大。

（2）对参数估计时，置信区间趋于变大。存在多重共线性时，参数估计量的方差增大，其标准误差也增大，导致总体参数的置信区间也随之变大。

（3）存在严重多重共线性时，**假设检验容易做出错误的判断。**存在严重多重共线性时，首先参数的置信区间扩大，会使得接受一个本应拒绝的假设的概率增大；此外在进行t检验时，在存在高度共线性时，参数估计值的方差增加较快，会使得t值变小（因为其参数标准误差增大）。而使本应否定的“系数为0”的原假设被错误地接受。

（4）当多重共线性严重时，可能造成可决系数R方较高，经F检验的参数联合显著性也很高，但对各个参数单独的t检验可能不显著，甚至可能使估计的回归系数符号相反，得出完全错误的结论。

第三节 多重共线性的检验

下面介绍几种常用的多重共线性的检验方法。

一、简单相关系数检验法

简单相关系数检验法是利用解释变量之间的线性相关程度去判断是否存在严重多重共线性的一种简便方法。一般而言，如果每两个解释变量的简单相关系数比较高，如大于0.8，则可认为存在着较严重的多重共线性。但要注意，有较高的简单相关系数只是多重共线性的充分条件，而不是必要条件。特别是在多元线性回归中，有时较低的简单相关系数也可能存在多重共线性。

二、方差扩大（膨胀）因子法

对于多元线性回归模型来说，如果分别以每个解释变量为被解释变量，作与其他解释变量的回归，这称为辅助回归。以Xj为被解释变量作对其他解释变量辅助线性回归的可决系数，用Rj方来表示，则可以证明，解释变量Xj参数估计值Bj估计的方差可表示为：

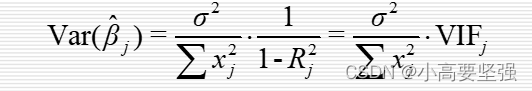
式中，VIF是变量Xj的方差扩大因子，即

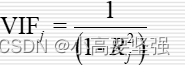
注意这里的VIFj是在多个解释变量辅助回归确定多重可决系数Rj方的基础上计算的方差扩大因子。由于Rj方度量了Xj对其他解释变量的线性相关程度，这种相关程度越强，说明变量间多重共线性越严重，VIFj也就越大。反之，Xj对其他解释变量的线性相关程度越弱，说明变量间的多重共线性越弱，VIFj也就越接近于1。

由此可见，VIFj的大小反映了解释变量之间存在多重共线性，可用它来度量多重共线性的严重程度。经验表明，VIFj>=10时，说明解释变量与其余解释变量之间有严重的多重共线性，且这种多重共线性可能会过度地影响最小二乘估计。

三、直观判断法

根据经验，通常一下情况地出现，可能提示存在着多重共线性的影响。
（1）当增加或剔除一个解释变量，或者改变一个观测值时，回归参数的估计值发生较大变化，回归方程可能存在严重的多重共线性。
（2）定性分析认为，一些重要的解释变量的回归系数的标准误差较大，在回归方程中没有通过显著性检验时，可初步判断可能存在严重的多重共线性。
（3）有些解释变量的回归系数所带正负号与定性结果相违背时，很可能存在多重共线性。
（4）模型的可决系数较高，F检验显著，但某些重要解释变量的偏回归系数t检验不显著，可能会存在多重共线性问题。

四、逐步回归检测法

逐步回归的基本思想是将变量逐个引入模型，每引入一个解释变量后。都要进行F检验，并对已经选入的解释变量逐个进行t检验，当原来引入的解释变量由于后面解释变量的引入而变得不显著时，将其提除。以确保每次引入新的变量之前回归方程只包含显著的变量。这是一个反复的过程，到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止。以确保最后所得到的解释变量集合是最优的。

在逐步回归中，如果解释变量之间是高度相关的，则先前引入的解释变量可能会因为后来引入与之相关的解释变量而被剔除。逐步回归用这种有进有出的结果说明解释变量之间是否具有较高的相关性。如果解释变量之间是完全不相关的，那么引入的解释变量就不会再被剔除，而剔除的解释变量也就不会再被引入。

第四节 多重共线性的补救措施

诊断出多重共线性，还需要采取一定的措施进行补救，以便降低回归模型中存在的多重共线性。

一、修正多重共线性的经验方法

1. 剔除变量法

当回归方程存在严重的多重共线性时，可以删除引起多重共线性的不重要的变量。一般而言，在选择回归模型时，可以将回归系数的显著性检验、方差扩大因子的多重共线性检验与解释变量经济含义（通过经济分析确定变量的相对重要性）结合起来考虑。

2. 增大样本容量

建立一个实际经济问题的回归模型，如果所收集的样本数据太少，是容易产生多重共线性的，这时，可以通过增大样本容量来减轻共线性的问题。

3. 变换模型形式

将原设定的模型形式作适当的变换，有可能消除或减弱原模型中解释变量之间的相关关系。例如可用差分法，这是将原模型变形为差分模型形式进而降低多重共线性。

通常，差分后变量之间的相关性要比差分前弱得多，但差分会丢失一部分信息，差分模型的误差项可能序列相关，可能会违背经典假设，在运用时要慎重。

4. 利用非样本先验信息

如果能够通过经济理论分析能够得到某些参数之间的线性关系，可以将这种线性关系作约束条件，将此约束条件和样本信息结合起来进行约束最小二乘估计。

5. 横截面数据与时序数据并用

首先利用横截面数据估计出部分参数，再利用时序数据估计出另外的部分参数，最后得到整个方程参数的估计。

注意：这里包含着假设，即参数的横截面估计和从纯粹时间序列分析中得到的估计是一样的。

6. 变量变换

有时能够通过对模型中的变量进行变换能够实现降低多重共线性的目的。例如：
（1）计算相对指标。如原来的是总量指标，可以计算人均指标或结构相对数指标等。
（2）将名义数据转换为实际数据。
（3）将小类指标合并为大类指标。例如建造业增加值与工业增加值合并为第二产业增加值。
（4）将总量指标进行对数变换。总量指标经过对数变换后，可将原来建立的线性回归模型转换为双对数模型，分析各解释变量的增减率对被解释变量增减率的影响。

需要指出，变量变换只是一种降低多重共线性的方法，有时可能得到较好的结果，有时也可能得不到较好的结果。

二、逐步回归法

依据逐步回归的思想，可逐步回归筛选并剔除引起多重共线性的变量。其具体步骤如下：先用被解释变量对每一个所考虑的解释变量作简单回归，然后以对被解释变量贡献最大的解释变量所对应的回归方程为基础，再逐个引入其余的解释变量。这个过程会出现以下三种情形：（1）若新变量的引入改变了调整后的R方和F检验，且其他回归参数的t检验在统计上仍然显著，则可考虑在模型中保留该变量；（2）若新变量的引入未能够明显改进调整后的R方和F检验，且对其他回归参数估计值的t检验也未带来什么影响，则认为该变量是多余的；（3）若新变量的引入未能明显改进调整后的R方和F检验，且显著地影响了其他回归参数估计值的数值或符号，致使某些回归参数也通不过t检验，则说明出现了严重的多重共线性。经过对各个引入新变量模型多方面的综合比较，保留调整后R方改进最大，且不影响原有变量显著性的模型。逐步回归使得最后保留在模型中的解释变量即是重要的，又没有严重的多重共线性。

逐步回归法的好处是将统计上不显著的解释变量剔除，最后保留在模型中的解释变量之间多重共线性不明显，而且对被解释变量有较好的解释贡献。但是应特别注意，逐步回归法可能因为剔除了重要的相干变量而导致设定偏误。

三、岭回归简介

为了降低多重共线性对回归模型的影响，计量经济学家还致力于改进古典最小二乘法，还提出以采用有偏的估计为代价来提高估计量的稳定性的方法，如岭回归、主成分法、偏最小二乘法等。下面主要简单地介绍岭回归法的思想和方法。

1. 岭回归的含义

岭回归是由A.E.Hoerl在1962年提出的一种改进最小二乘估计的方法，也叫岭估计。

当解释变量之间存在多重共线性时，X’X的行列式接近于0，所以可在其基础上加一个正常数对角矩阵，即X’X+kI，使得它的行列式等于0的可能性更小。这样就可以求得参数的估计值，也叫岭回归估计量。其中k为零回归参数。

当解释变量之间存在多重共线性时，使用岭估计应比最小二乘估计稳定，当k较小时，回归系数很不稳定，而当k逐渐增大时，回归系数可能呈现稳定状态。因此，要选择合适的k值，岭回归参数才会优于普通最小二乘估计参数。当k=0时，岭估计就是普通最小二乘估计。

2. 岭回归估计的性质

（1）岭回归的参数估计是回归系数的有偏估计。
（2）在岭回归参数k与Y无关的情形下，B(k)估计是最小二乘估计的一个线性变换，也是理论值Y的线性函数。
（3）可以证明岭回归估计量B(k)估计方差比普通最小二乘估计B的估计方差要小。（估计量更加有效）

岭回归估计的方差和偏倚与岭回归参数k有关，岭回归参数k的值越大，B(k)估计的偏倚越大，其方差越小。要得到方差较小的估计结果，就不得不牺牲无偏性。为此可以用兼顾方差和偏倚的最小均方误差原则（MSE），去分析岭回归的效果。

3. 岭回归参数k的选择

原则上是选择是MSE(B(k)估计)达到最小的k，而最优k值依赖于未知参数B和防方差o方，因而在实际应用中必须通过样本来确定。目前话没有形成一个公认的最优方法。但常用的方法主要有岭迹法、方差扩大因子法、残差平方和方法。在实际应用中，可考虑使用逐步搜索的方法，即开始给定较小的k值，然后逐渐增加k的取值进行实验，直至岭回归估计量B(k)估计的值趋于稳定。

显然，用逐步搜索的方法确定的k值，仍缺乏令人信服的理论依据，具有一定的主观性，是一种将定性和定量分析相结合的方法。

与岭回归相似的方法还有Lasso回归、适应性Lasso回归；多元统计技术中的因子分析、主成分分析及偏最小二乘回归也常用于“解决”多重共线性问题。

本文主要参考庞皓计量经济学第三版