数据库索引一二事（二）--B+树结构_索引树结构

B+树和B树基本差不多，但是存在一些差异。

B+树的总结：

1.根结点只有1个，分支数量范围[2,m]。

2.除根以外的非叶子结点，每个结点包含分支数范围[Ceil[m/2],m]，m=3的话就是[2,3]。

3.所有非叶子节点的关键字数目等于它的分支数量。（这一点在学习B+树时是有争议的，具体参见下面两个两个链接）

    3.1 维基百科

    3.2 个人博客

4.所有叶子节点都在同一层，且关键字数目范围是[Ceil[m/2]-1,m-1]，m=3的话就是[1,2]（这一点就是基于第3点出来的，这里我们采用维基百科的说明方式，和B树保持一致，这样好理解一点）。

5.叶子节点包含全部关键字的信息(非叶子节点只包含索引)，且叶子结点中的所有关键字依照大小顺序链接(所以一个B+树通常有两个头指针，一个是指向根节点的root，另一个是指向最小关键字的sqt)。

B+和B树的不同点比较

1.关键字的不同：

    B+树的关键字和字树相关，n棵字树就有n个关键字（有的地方说是n棵字数有n-1个关键字，这和B树一样）。

    B树的关键字也和字树相关，类比上一篇文章，n棵字树有n-1个关键字。（但是关键字还是存在一个范围）。

2.叶子节点的不同：

    B+树的叶子节点包含全部关键字信息，以及这些关键字的指针，而且叶子节点本身按照大小顺序链接。

    B树的叶子节点只包含当前节点的信息，没有全部的信息，而且叶子节点也没有按照顺序链接。

3.非叶子节点：

    B+树的非叶子节点可以看做是索引部分，只存储最大或者最小关键字。

    B树的非叶子节点包含了全部信息。

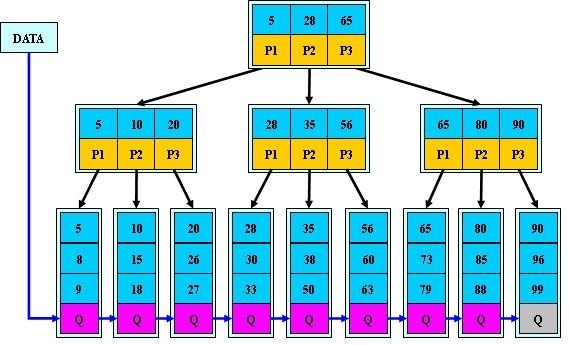
以M=3为例（因此由于关键字数目存在争议，此图也大致看下，不影响其他的学习，只是关键字数目不一致而已）：

B+树的插入：

我们这一次先以5阶为例子来分析。依照上面的分析来对应数字。其实我们去学习B+树的时候，个人观点主要是要知道它的非叶子节点只保存了索引，真正的数据是存在于叶子节点上

1.根节点下面的分支数目是 [2,5]。

2.非叶节点分支数[3,5]。--->这里也和B树一致。

3.不考虑，数目，只是一个规定。

4.叶子节点关键字数目是[2,4]。--->这里和B树一致

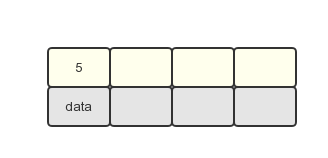
1.插入第一个关键字 5

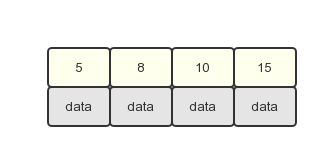
2.然后依次插入8,10,15，刚好是最大值4，所以不会引起分裂操作。

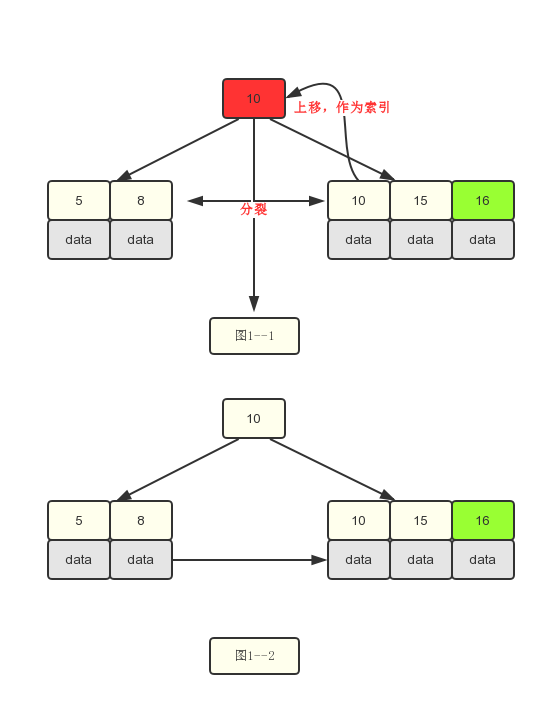
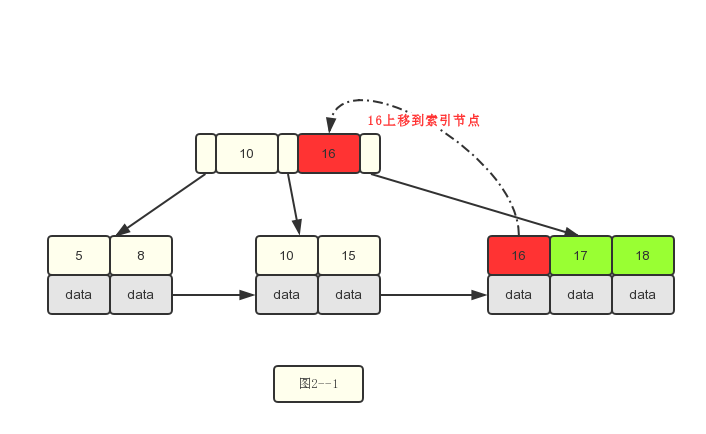
3.插入16

4.插入17和18.插入17时，没问题，插入18时需要分裂了。

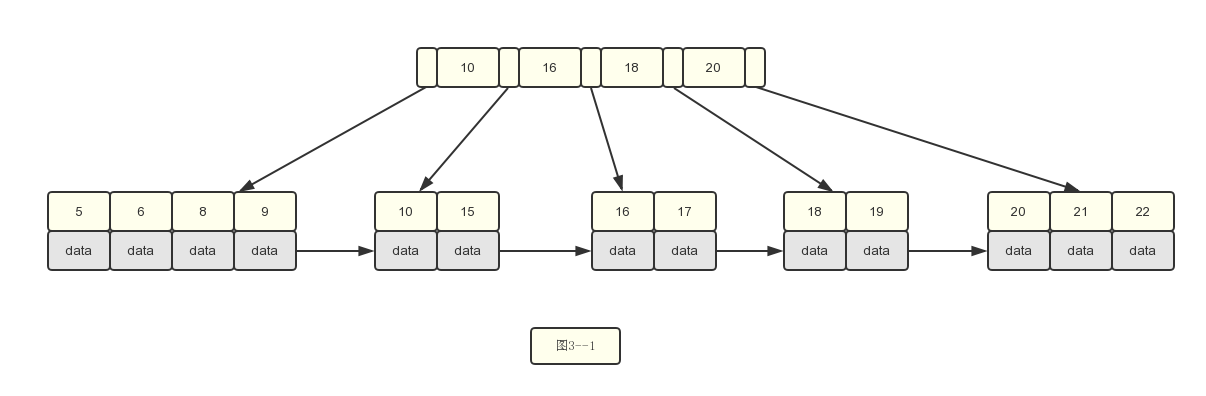
5.插入若干数据之后的情况如下：

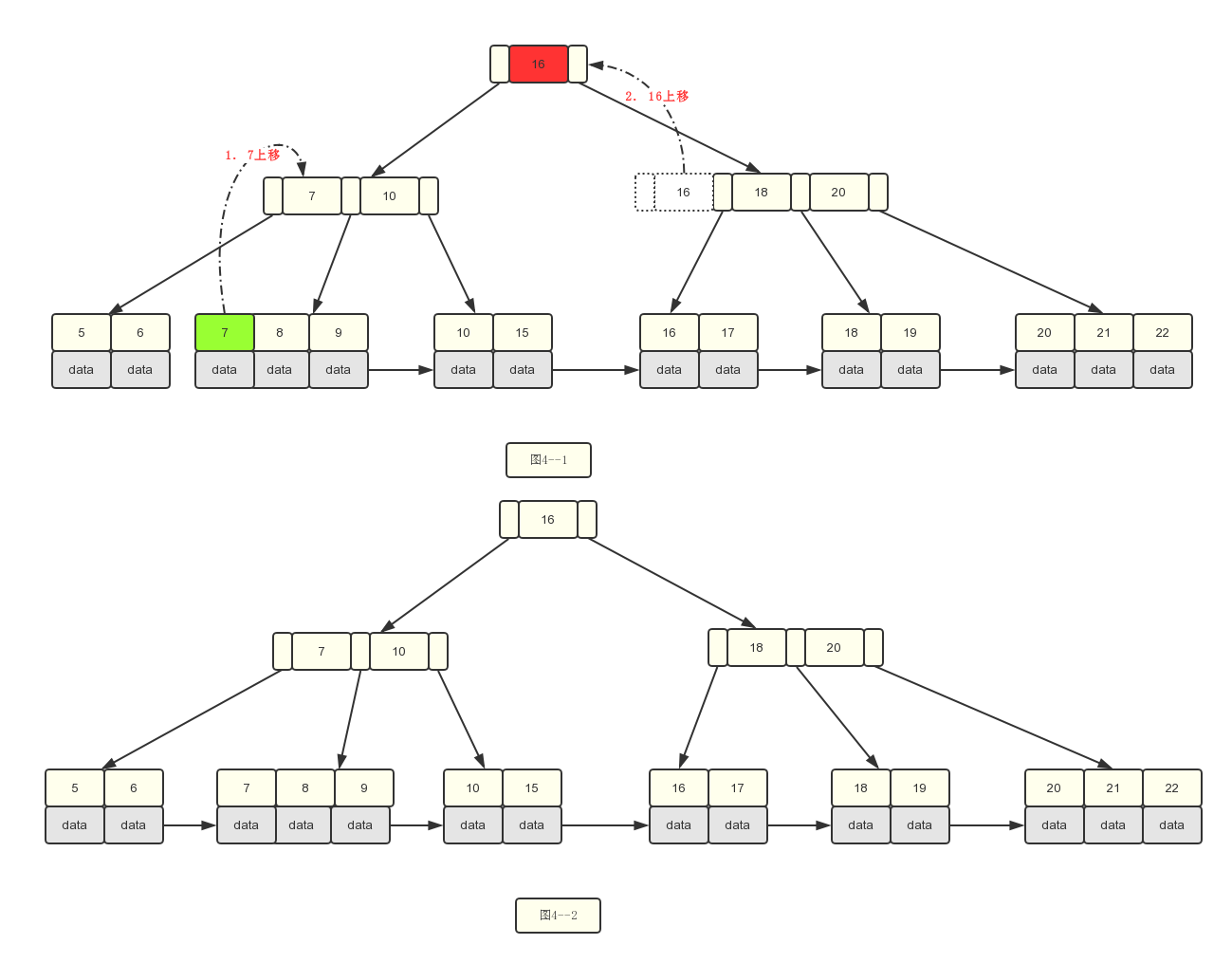
6.插入数据7.

基本上插入的过程就是上面的流程，上面的插入基于的是关键比节点数-1的情况，关键字和节点数相等的情况其实分裂过程都是一样，总结一下插入流程：

1.空树的时候直接创建一个叶子节点，插入过程结束。

2.针对当前是叶子节点：继续插入时，如果关键字数目小于m-1，结束。如果大于了m-1。则需要进行分裂成两个叶子节点，此过程中需要将右边节点的第一个关键字上移去父节点作为索引数据。

3.针对当前是索引类型节点时，需要将中间索引节点上移到父节点，左边指向左孩子，右边指向右孩子，需要注意索引和叶子节点分裂时有点不同的地方在于叶子节点上移时本身还存在于叶子节点上。

B+树的删除

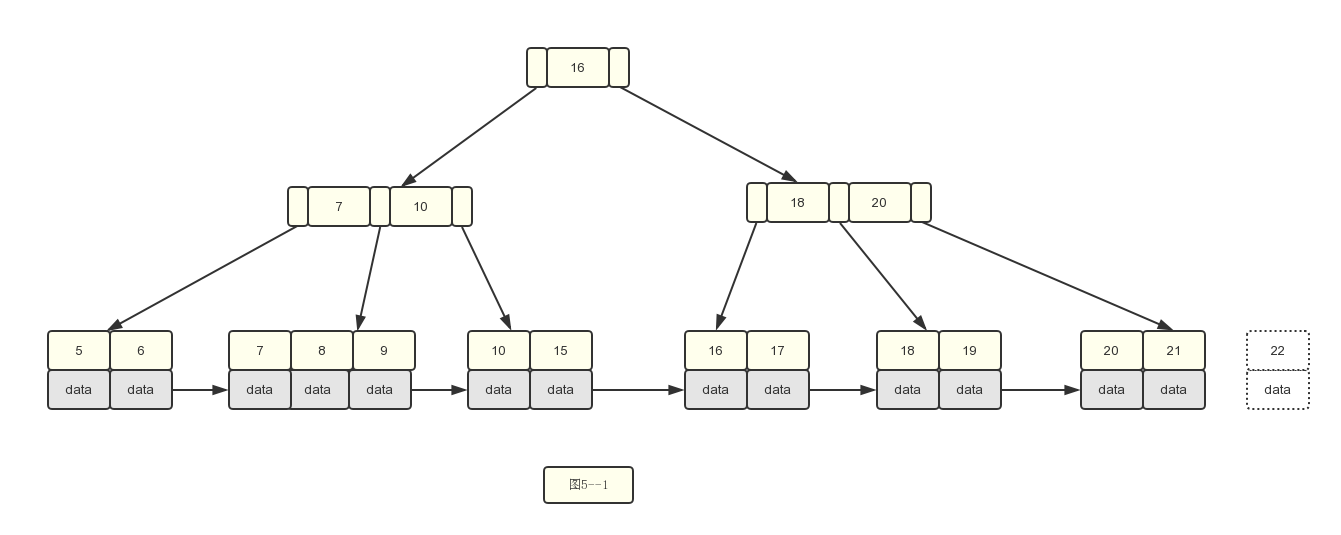
1.基于图4--2，我们删除22，没有任何变动，只要删除就行

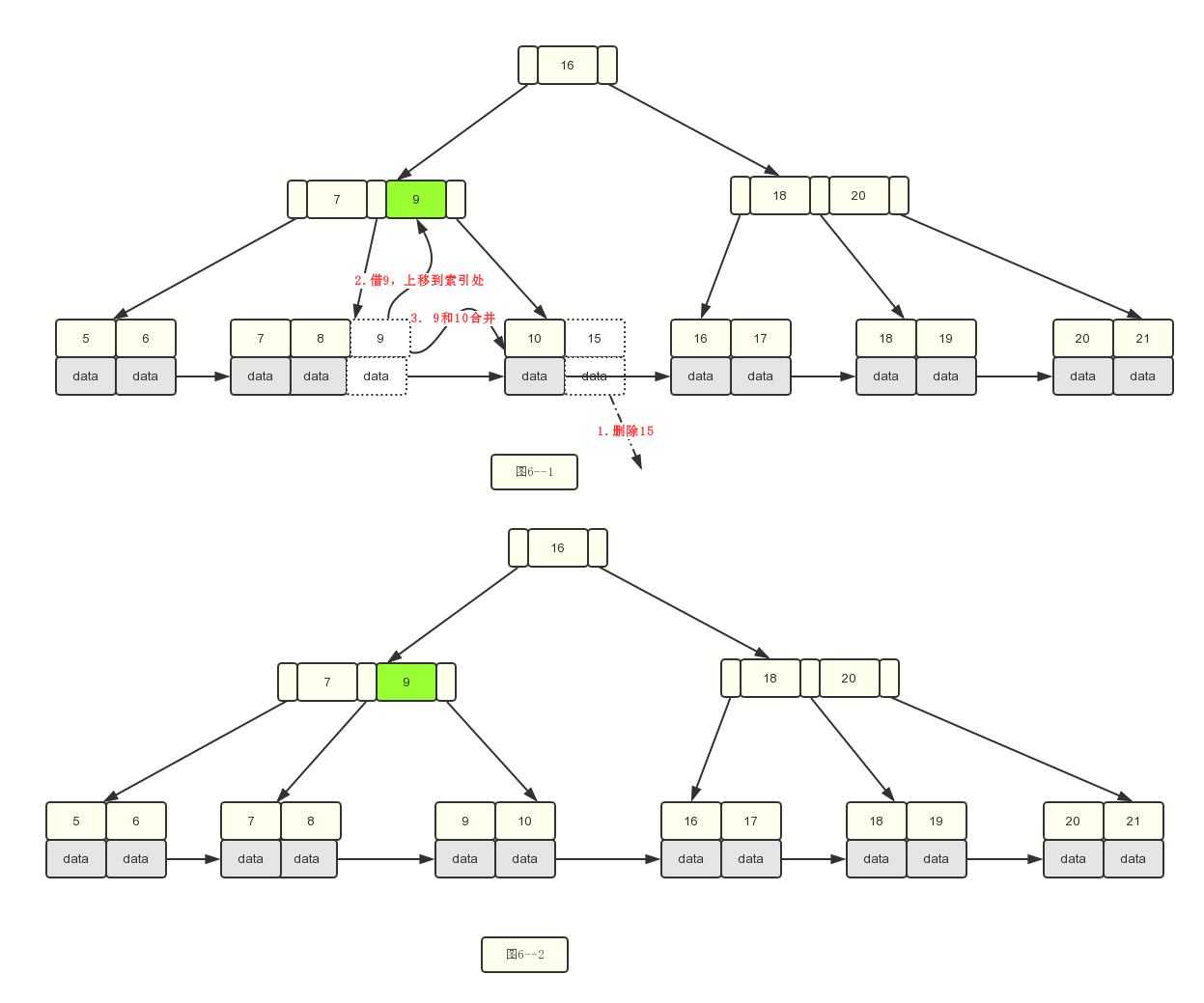
2.删除15关键字

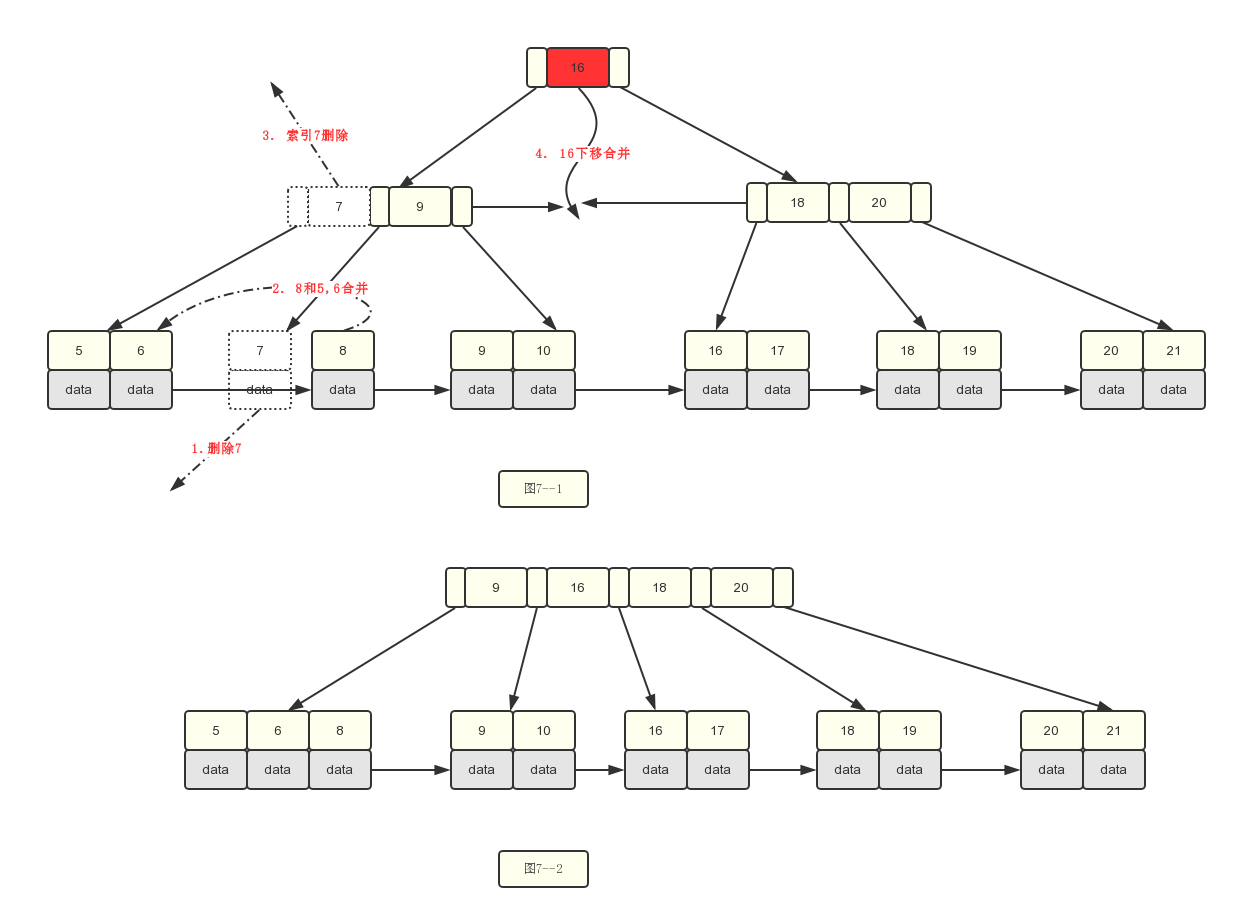
3.基于图6--2删除7关键字

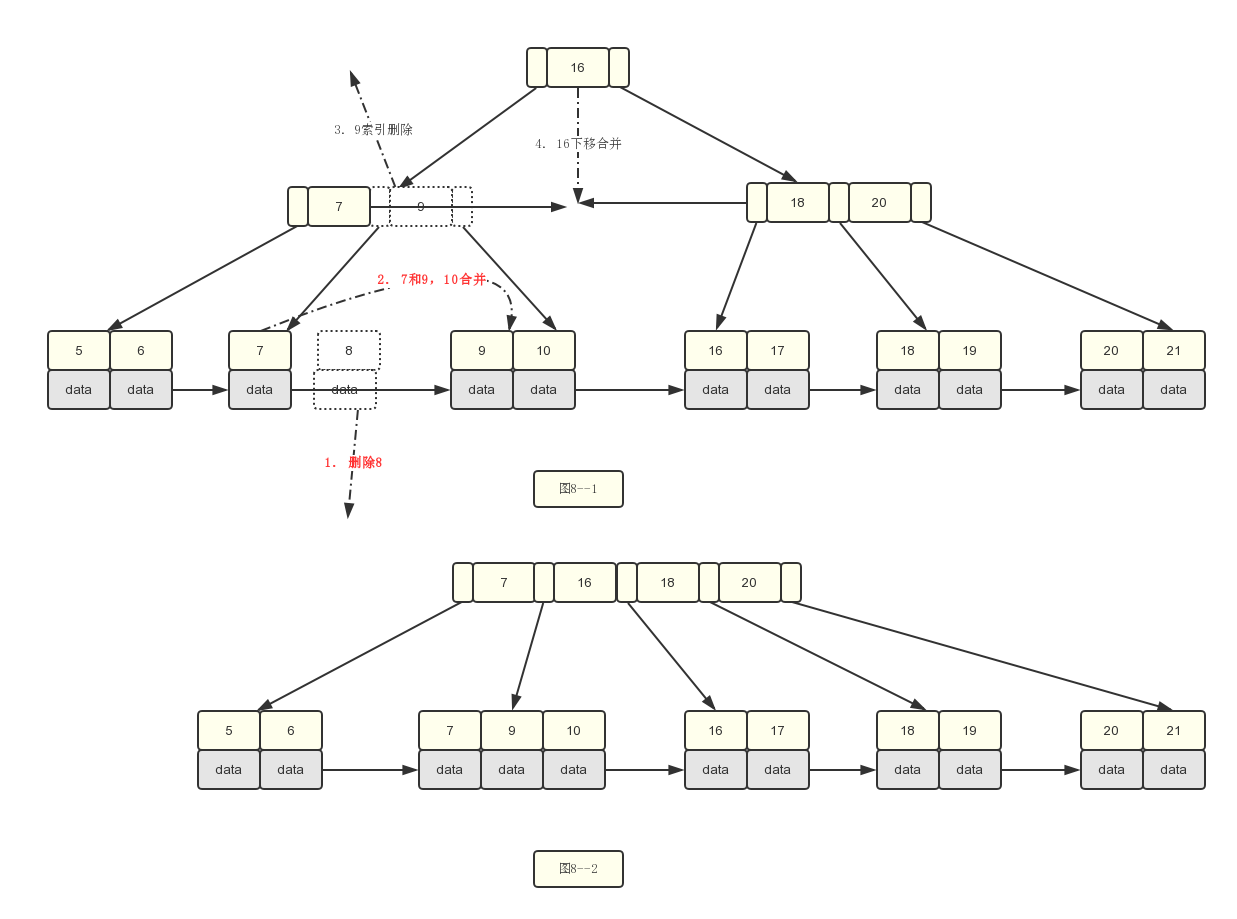
4.多分析一种场景，如果我删除的是关键字8呢？其实不管怎么删除，索引结构中是需要跟着变动的，比如说删除8的时候 7和5,6节点合并，那么7这个索引就需要删除，只能留下9，一个道理。

B+树的删除不总结了，其实和B树差不多（因为本篇文章的关键字是和B树一样的），所以分析起来特别容易，B树的删除还稍微复杂，复杂的地方在于B树里面每一个节点（叶子节点和非叶子节点）都保存了数据，需要不断移动以保证B树的特性，但是B+树里面删除的只能是叶子节点，需要同时保持更新的只是索引的关键字而已，所以简单了不少。

参考：

B+树的介绍

B+树bug分析