【数据结构】二叉树--链式结构_数据结构找树的叶子节点的算法

普通二叉树增删查改没有价值，单纯为了存储数据，不如使用线性表。

学习普通二叉树是为更好的控制它的结构，为后续学习更加复杂的搜索二叉树打基础。

平衡二叉树：AVL树，红黑树。

二叉树的概念：

1.空树

2.非空：根节点，根结点的左子树，根结点的右子树组成。

二叉树的概念：

1.空树

2.非空：根节点，根结点的左子树，根结点的右子树组成。

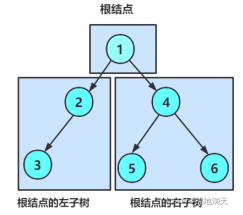
根据概念可知：二叉树定义是递归的，因此后续基本操作按照递归进行。

二叉树的遍历

前序，中序，后续遍历

模拟遍历

1.前序遍历（先根遍历）：根 左子树 右子树 

                          1  2  3  4  5  6

2.中序遍历（中根遍历）：左子树，根结点 ，右子树

                                 3  2  1  5  4  6

3.后序遍历（后根遍历）：左子树，右子树，根

                         3  2  5  6  4  1

层序遍历：1  2  4  3  5  6

模拟实现二叉树遍历

构建链式结构

typedef int BTDataType;
 
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;//左树节点
	struct BinaryTreeNode* right;//右数节点
	BTDataType data;//节点值
}BTNode;
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
BTNode* BuyBTNode(BTDataType x)
{
	//malloc节点
	BTNode* tmp = (BTNode*)malloc(sizeof(BTNode));
	if (tmp == NULL)
	{
		printf("malloc failed!\n");
		exit(-1);
	}
	BTNode* node = tmp;
	node->left = node->right = NULL;
	node->data = x;
	return node;
}
//手动创建链式二叉树
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyBTNode(1);
	BTNode* node2 = BuyBTNode(2);
	BTNode* node3 = BuyBTNode(3);
	BTNode* node4 = BuyBTNode(4);
	BTNode* node5 = BuyBTNode(5);
	BTNode* node6 = BuyBTNode(6);
 
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
 
	return node1;
}

1.前序遍历

基本思路：根 - 左数- 右数

void PrevOrder(BTNode* tree)
{
 
	if (tree == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", tree->data);
	PrevOrder(tree->left);
	PrevOrder(tree->right);
}

 

 

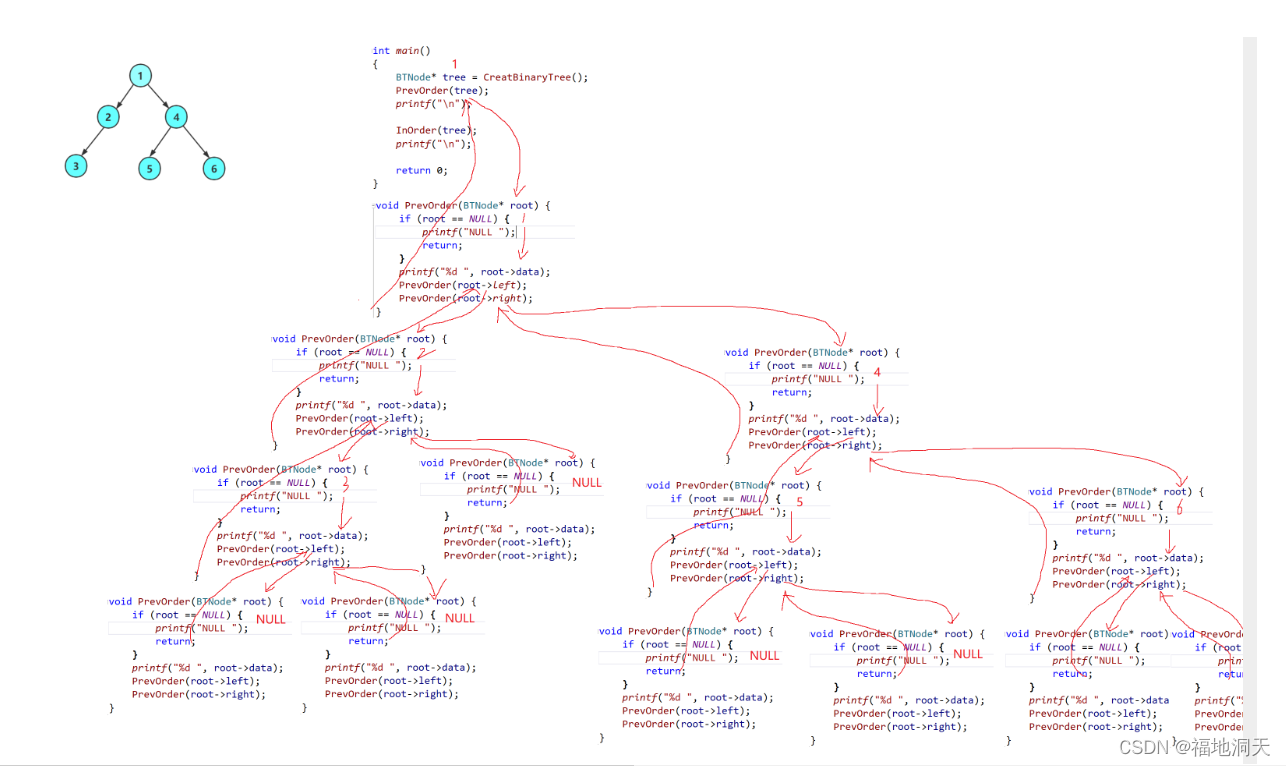
2.中序遍历

左子树 - 根结点  - 右子树

//中序遍历
void InOrder(BTNode* tree)
{
	if (tree == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(tree->left);
	printf("%d ", tree->data);
	InOrder(tree->right);
}

 

 

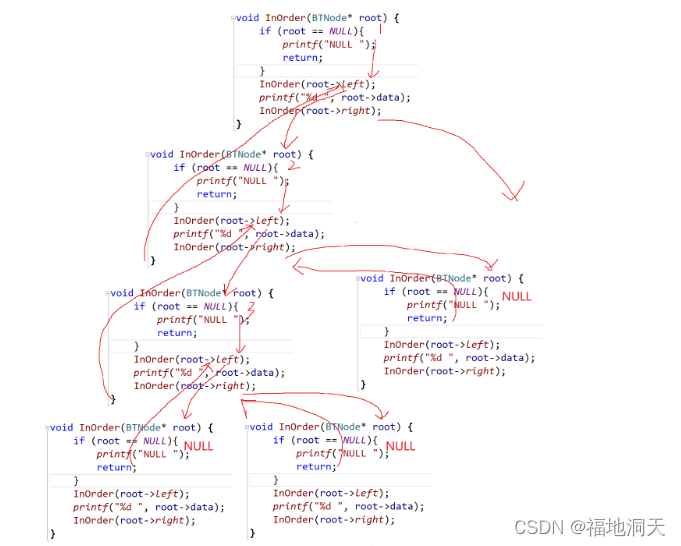
3.后序遍历

左子树- 右子树- 根

//后序遍历
void NextOrder(BTNode* tree)
{
	if (tree == NULL)
	{
		printf("NULL ");
		return;
	}
	NextOrder(tree->left);
	NextOrder(tree->right);
	printf("%d ", tree->data);
}

 

4.求节点个数

a.遍历＋计数

第一种：

1.遍历+计数
void BTSize(BTNode* tree, int* pCount)
{
	if (tree == NULL)
		return;
 
	(*pCount)++;
	BTSize(tree->left,pCount);
	BTSize(tree->right, pCount);
}

第二种：

定义一个全局遍历的计数器或者static定义一个静态局部变量。

int count = 0;
int BTSize(BTNode* tree)
{
	
	//static int count = 0;
	if (tree == NULL)
		return count;
	count++;
	BTSize(tree->left);
	BTSize(tree->right);
 
	return count;
}

但这有一个致命的错误，多次调用返回的节点个数会错误。

原因：全局变量和静态局部变量都没办法没初始化为0。

b.分治：

分治思想：将复杂的问题分成规模更小的子问题，子问题再分为更小的子问题，……

方法：计算完左子树的节点个数再加上右节点的个数。

思想：递归

//分治
/*把复杂的问题，分成更小规模的子问题，子问题再分为更小的子问题……*/
 
//左子树算完再算右数再加上根节点
int BTSize(BTNode* tree)
{
	if (tree == NULL)
		return 0;
	return BTSize(tree->left) + BTSize(tree->right) + 1;
}

5.求叶子节点的个数

分治：计算完左树再计算完右树。

代码：

//求叶子结点的个数
//分治
int BTreeLeafSize(BTNode* tree)
{
	if (tree == NULL)
		return 0;
	if (tree->left == NULL && tree->right == NULL)
		return 1;
	return BTreeLeafSize(tree->left) + BTreeLeafSize(tree->right);
}

6.求第k层节点的个数

思路：将第k-1层的作为父亲节点，递推。

//第k层节点的个数
 
int BTreeLevelSize(BTNode* tree,int k)
{
	assert(k >= 1);
	if (tree == NULL)
		return 0;
	if (k == 1)
		return 1;
	//找到k-1层作为父亲节点，计算即可
	return BTreeLevelSize(tree->left,k-1) + BTreeLevelSize(tree->right,k-1);
}

7.问树高几何？

分治：计算左子树高度和右子树高度作比较，大的那个+1

//求树高几何？
int BTreeDepth(BTNode* tree)
{
	//分治，左数算出高来，右数算出高来，比较取其大者
	if (tree == NULL)
		return 0;
	return BTreeDepth(tree->left) > BTreeDepth(tree->right) ? BTreeDepth(tree->left) + 1 : BTreeDepth(tree->right) + 1;
}

8.二叉树查找值为x的节点

1. 思路：1）考虑分治思想，先递归左树，再递归右树。
2. 2）找到就返回对应节点地址，炸藕到就返回NULL
3. 3）判断返回的是为NULL 还是 对应的节点。

//二叉树查找为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	//前序遍历
	if (root->data == x)
		return root;
	//先遍历左树
	BTNode* ret1 = BinaryTreeFind(root->left,x);
	if (ret1)
		return ret1;
	//遍历右树
	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;
	return NULL;
}

9.层序遍历

思路：根据层序遍历的特性，可以使用队列解决。

当取出上一层的数据的时候，将上一层对应的left 和 right 入队列。

注意：C由于没有库，要取出我们之前自己实现的队列的文件，添加在该项目的相应位置。

记得在Queue.h上加入

入队列的时候，入的是二叉树的一整个结构体，不单单是data

代码：

//层序遍历
/*根据层序遍历的特性，考虑将数据入队列，可以根据队列的性质，实现层序遍历
当取出上一层数据的时候，将left 和 right 节点依次入队列*/
void LevelOrder(BTNode* tree)
{
	//创建队列
	Queue q;
	QueueInit(&q);
	
	//树不为空，入队列
	if (tree)
	{
		QueuePush(&q,tree);
	}
	//将数据入队列。
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		
		//如果左子树不为空，入队列
		if (front->left)
			QueuePush(&q, front->left);
		//如果右树不为空，入队列
		if (front->right)
			QueuePush(&q, front->right);
	}
	printf("\n");
	//销毁队列
	QueueDestory(&q);
}

 

10.判断二叉树是否为完全二叉树

思路：判断还是以队列为基础，层序遍历为辅。

入队列时，NULL也入队列，当出队列的时候遇到NULL时，开始将剩下的队列数据除队列，当剩下的数据中只有NULL时，则说明其是完全二叉树，否则就不是。

画图：

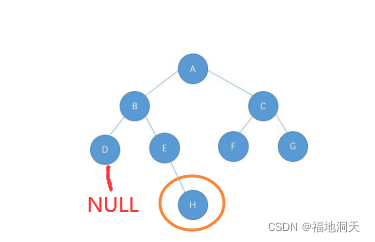
这棵树就不是完全二叉树。

代码：

//判断二叉树是否为完全二叉树
/*以队列为基础，层序遍历为辅助，当遇到NULL时，将剩下的数据都出队列，当剩下的数据中只有NULL，
则说明是完全二叉树，否则就不是文强案二叉树*/
 
bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	//若不为空，入队列
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//为空时跳出
		if (front == NULL)
			break;
		//入队列
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
			return false;
	}
	return true;
}

11.销毁树

思路：递归分治，销毁左子树 - 右子树 - 根

void BTreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	BTreeDestroy(root->left);
	BTreeDestroy(root->right);
	free(root);
}

如有错误，还请大佬们指出~