【论文笔记】Long Tail Learning via Logit Adjustment_logits adjustment

摘要

Our techniques revisit the classic idea of logit adjustment based on the label frequencies, either applied post-hoc to a trained model, or enforced in the loss during training. Such adjustment encorages a large relative margin between logits of rare versus dominant labels.
重温了基于标签频率的逻辑调整，并将这种logit adjustment应用在训练前还是还是训练中。这种调整是支持原始的logit和主类之间的相对边界。 available at: https://github.com/google-research/google-research/tree/master/logit_adjustment

引言

Owing to this paucity of samples, generalisation on such labels is challenging; moreover, naive learning on such data is susceptible to an undesirable bias towards dominant labels. This problem has been widely studied in the literature on learning under class imbalance and the related problem of cost-sensitive learning.

Recently, long-tail learning has received renewed interest in the context of neural networks. Two active strands of work involve post-hoc normalisation weights, and modification of the underlying loss to account for varying class penalties. However, weight normalisation crucially relies on the weight norms being smaller for rare classes; however, this assumption is sensitive to the choice of optimiser. On the other hand, loss modification sacrifices the consistency that underpins the softmax cross-entropy.

Conceptually, logit adjustment encourages a large relative margin between a pair of rare and dominant labels. logit adjustment is endowed with a clear statistical grounding: by construction, the optimal solution under such adjustment coincides with the Bayes-optimal solution for the balanced error, i.e., Fisher consistent for minimising the balanced error.

Limitations of existing approaches

有趣的发现

（1）limitations of weight normalisation
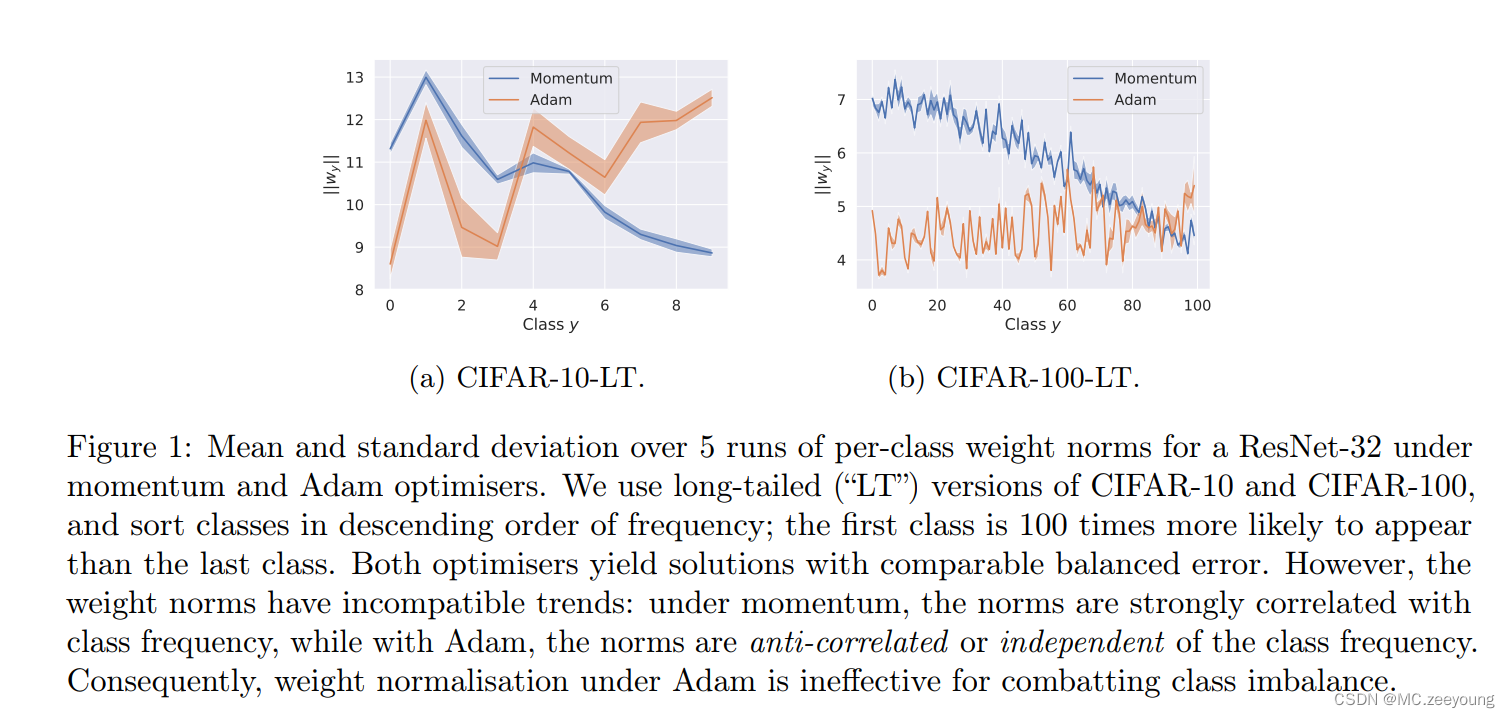
Kang et al. [2020] is motivated by the observation that the weight norm ||wy||2 tends to correlate with P. However, we now show this assumption is highly dependent on the choice of optimizer.
We optimise a ResNet-32 using both SGD with momentum and Adam optimisers. Figure 1 confirms that under SGD, ||wy||2 and the class priors P are correlated. However , with Adam, the norms are either anti-correlated or independent of the class priors. This marked difference may be understood in lightof recent study of the implicit bias of optimises.

(2) limitations of loss modification
current loss are not consistent in this sense, even for binary problems. Here , we consider that current loss consider the frequency of positive or negative, but not both simultaneously.

方法

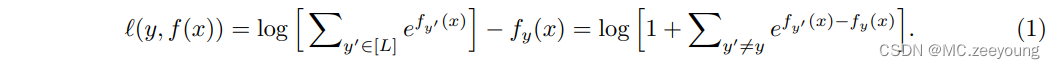
把红框去掉那就是softmax Cross Entropy

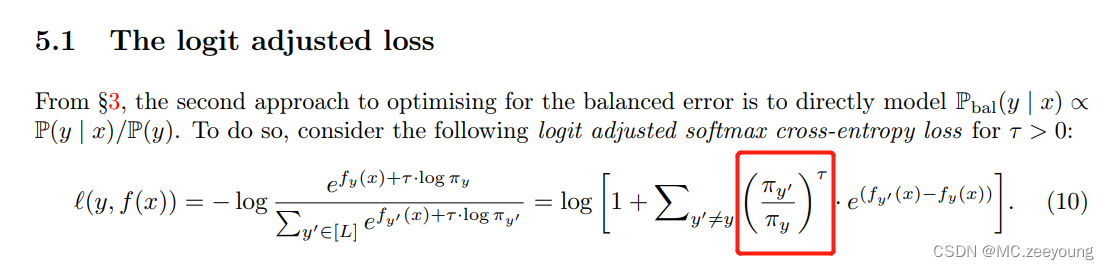
其中，