机器学习算法---K近邻算法

K近邻算法

1. K-近邻算法简介

1.1 什么是K-近邻算法

根据你的“邻居”来推断出你的类别

• K Nearest Neighbor算法⼜叫KNN算法，这个算法是机器学习⾥⾯⼀个⽐较经典的算法， 总体来说KNN算法是相对⽐ 较容易理解的算法

如果⼀个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的⼤多数属于某⼀个类别，则该样本也属于这个 类别。

1.1.1 距离公式

两个样本的距离可以通过如下公式计算，⼜叫欧式距离 ，关于距离公式会在后⾯进⾏讨论

1.2 KNN算法流程总结

1）计算已知类别数据集中的点与当前点之间的距离
2）按距离递增次序排序
3）选取与当前点距离最⼩的k个点
4）统计前k个点所在的类别出现的频率
5）返回前k个点出现频率最⾼的类别作为当前点的预测分类

2. k近邻算法api初步使⽤

机器学习流程：

1.获取数据集
2.数据基本处理
3.特征⼯程
4.机器学习
5.模型评估

2.1 Scikit-learn⼯具介绍

Python语⾔的机器学习⼯具
Scikit-learn包括许多知名的机器学习算法的实现
Scikit-learn⽂档完善，容易上⼿，丰富的API
⽬前稳定版本0.19.1

2.1.1 安装

注：安装scikit-learn需要Numpy, Scipy等库
pip3 install scikit-learn==0.19.1

2.1.2 Scikit-learn包含的内容

• 分类、聚类、回归
• 特征⼯程
• 模型选择、调优

2.2 K-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
n_neighbors：int,可选（默认= 5），k_neighbors查询默认使⽤的邻居数

3. 距离度量

3.1 距离公式的基本性质

在机器学习过程中，对于函数 dist(., .)，若它是⼀"距离度量" (distance measure)，则需满⾜⼀些基本性质:

3.2 常⻅的距离公式

3.2.1 欧式距离(Euclidean Distance)：

3.2.2 曼哈顿距离(Manhattan Distance)：

在曼哈顿街区要从⼀个⼗字路⼝开⻋到另⼀个⼗字路⼝，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是 “曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

3.2.3 切⽐雪夫距离 (Chebyshev Distance)：

国际象棋中，国王可以直⾏、横⾏、斜⾏，所以国王⾛⼀步可以移动到相邻8个⽅格中的任意⼀个。国王从格⼦(x1,y1) ⾛到格⼦(x2,y2)最少需要多少步？这个距离就叫切⽐雪夫距离。

3.3.4 闵可夫斯基距离(Minkowski Distance)：

闵⽒距离不是⼀种距离，⽽是⼀组距离的定义，是对多个距离度量公式的概括性的表述。 两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

根据p的不同，闵⽒距离可以表示某⼀类/种的距离
⼩结：

1. 闵⽒距离，包括曼哈顿距离、欧⽒距离和切⽐雪夫距离，都存在明显的缺点:
   e.g. ⼆维样本(身⾼[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。 a与b的闵⽒距离（⽆论是曼哈顿距离、欧⽒距离或切⽐雪夫距离）等于a与c的闵⽒距离。但实际上身⾼的10cm并不能 和体重的10kg划等号。
2. 闵⽒距离的缺点： (1)将各个分量的量纲(scale)，也就是“单位”相同的看待了; (2)未考虑各个分量的分布（期望，⽅差等）可能是不同的。

3.3 “连续属性”和“离散属性”的距离计算

我们常将属性划分为 “连续属性” (continuous attribute)和 “离散属性” (categorical attribute)，前者在定义域上有⽆穷多个 可能的取值，后者在定义域上是有限个取值.

• 若属性值之间存在序关系，则可以将其转化为连续值，例如：身⾼属性“⾼”“中等”“矮”，可转化为{1, 0.5, 0}。 闵可夫斯基距离可以⽤于有序属性。
• 若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“⼥”，可转化为{（1,0）， （0,1）}。

4. k值的选择

4.1 K值选择说明

• K值过⼩： 容易受到异常点的影响
• k值过⼤： 受到样本均衡的问题

K值选择问题，李航博⼠的⼀书「统计学习⽅法」上所说

5 kd树

5.1 kd树简介

5.1.1 什么是kd树

根据KNN每次需要预测⼀个点时，我们都需要计算训练数据集⾥每个点到这个点的距离，然后选出距离最近的k个点进⾏投票。当数据集很⼤时，这个计算成本⾮常⾼，针对N个样本，D个特征的数据集，其算法复杂度为O（DN ）。 kd树：为了避免每次都重新计算⼀遍距离，算法会把距离信息保存在⼀棵树⾥，这样在计算之前从树⾥查询距离信息， 尽量避免重新计算。其基本原理是，如果A和B距离很远，B和C距离很近，那么A和C的距离也很远。有了这个信息， 就可以在合适的时候跳过距离远的点。 这样优化后的算法复杂度可降低到O（DNlog（N））。感兴趣的读者可参阅论⽂：Bentley，J.L.，Communications of the ACM（1975）。 1989年，另外⼀种称为Ball Tree的算法，在kd Tree的基础上对性能进⼀步进⾏了优化。

5.1.2 原理

⻩⾊的点作为根节点，上⾯的点归左⼦树，下⾯的点归右⼦树，接下来再不断地划分，分割的那条线叫做分割超平⾯ （splitting hyperplane），在⼀维中是⼀个点，⼆维中是线，三维的是⾯。

⻩⾊节点就是Root节点，下⼀层是红⾊，再下⼀层是绿⾊，再下⼀层是蓝⾊。

1.树的建⽴；
2.最近邻域搜索（Nearest-Neighbor Lookup）
kd树(K-dimension tree)是⼀种对k维空间中的实例点进⾏存储以便对其进⾏快速检索的树形数据结构。kd树是⼀种⼆叉 树，表示对k维空间的⼀个划分，构造kd树相当于不断地⽤垂直于坐标轴的超平⾯将K维空间切分，构成⼀系列的K维超 矩形区域。kd树的每个结点对应于⼀个k维超矩形区域。利⽤kd树可以省去对⼤部分数据点的搜索，从⽽减少搜索的计

类⽐“⼆分查找”：给出⼀组数据：[9 1 4 7 2 5 0 3 8]，要查找8。如果挨个查找（线性扫描），那么将会把数据集都遍历 ⼀遍。⽽如果排⼀下序那数据集就变成了：[0 1 2 3 4 5 6 7 8 9]，按前⼀种⽅式我们进⾏了很多没有必要的查找，现在 如果我们以5为分界点，那么数据集就被划分为了左右两个“簇” [0 1 2 3 4]和[6 7 8 9]。 因此，根本就没有必要进⼊第⼀个簇，可以直接进⼊第⼆个簇进⾏查找。把⼆分查找中的数据点换成k维数据点，这样 的划分就变成了⽤超平⾯对k维空间的划分。空间划分就是对数据点进⾏分类，“挨得近”的数据点就在⼀个空间⾥⾯。

5.2 构造⽅法

（1）构造根结点，使根结点对应于K维空间中包含所有实例点的超矩形区域；
（2）通过递归的⽅法，不断地对k维空间进⾏切分，⽣成⼦结点。在超矩形区域上选择⼀个坐标轴和在此坐标轴上的⼀ 个切分点，确定⼀个超平⾯，这个超平⾯通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个 ⼦区域（⼦结点）；这时，实例被分到两个⼦区域。
（3）上述过程直到⼦区域内没有实例时终⽌（终⽌时的结点为叶结点）。在此过程中，将实例保存在相应的结点上。
（4）通常，循环的选择坐标轴对空间切分，选择训练实例点在坐标轴上的中位数为切分点，这样得到的kd树是平衡的 （平衡⼆叉树：它是⼀棵空树，或其左⼦树和右⼦树的深度之差的绝对值不超过1，且它的左⼦树和右⼦树都是平衡⼆ 叉树）。
KD树中每个节点是⼀个向量，和⼆叉树按照数的⼤⼩划分不同的是，KD树每层需要选定向量中的某⼀维，然后根据这 ⼀维按左⼩右⼤的⽅式划分数据。在构建KD树时，关键需要解决2个问题：
（1）选择向量的哪⼀维进⾏划分；
（2）如何划分数据；
第⼀个问题简单的解决⽅法可以是随机选择某⼀维或按顺序选择，但是更好的⽅法应该是在数据⽐较分散的那⼀维进⾏ 划分（分散的程度可以根据⽅差来衡量）。
第⼆个问题中，好的划分⽅法可以使构建的树⽐较平衡，可以每次选择中位数来进⾏划分。

5.3 案例分析

5.3.1 树的建⽴

（1）思路引导：
根结点对应包含数据集T的矩形，选择x(1)轴，6个数据点的x(1)坐标中位数是6，这⾥选最接近的(7,2)点，以平⾯x(1)=7 将空间分为左、右两个⼦矩形（⼦结点）；接着左矩形以x(2)=4分为两个⼦矩形（左矩形中{(2,3),(5,4),(4,7)}点的x(2)坐 标中位数正好为4），右矩形以x(2)=6分为两个⼦矩形，如此递归，最后得到如下图所示的特征空间划分和kd树。

5.3.2 最近领域的搜索

假设标记为星星的点是 test point， 绿⾊的点是找到的近似点，在回溯过程中，需要⽤到⼀个队列，存储需要回溯的点，在判断其他⼦节点空间中是否有可能有距离查询点更近的数据点时，做法是以查询点为圆⼼，以当前的最近距离为 半径画圆，这个圆称为候选超球（candidate hypersphere），如果圆与回溯点的轴相交，则需要将轴另⼀边的节点都放 到回溯队列⾥⾯来。

样本集{(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)}

1 查找点(2.1,3.1)

在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2),(5,4), (2,3)>，从search_path中 取出(2,3)作为当前最佳结点nearest, dist为0.141； 然后回溯⾄(5,4)，以(2.1,3.1)为圆⼼，以dist=0.141为半径画⼀个圆，并不和超平⾯y=4相交，如上图，所以不必跳到结 点(5,4)的右⼦空间去搜索，因为右⼦空间中不可能有更近样本点了。
于是再回溯⾄(7,2)，同理，以(2.1,3.1)为圆⼼，以dist=0.141为半径画⼀个圆并不和超平⾯x=7相交，所以也不⽤跳到结 点(7,2)的右⼦空间去搜索。 ⾄此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

2 查找点(2,4.5)

在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)【优先选择在本域搜索】，然后search_path中的结点为<(7,2),(5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；
然后回溯⾄(5,4)，以(2,4.5)为圆⼼，以dist=3.202为半径画⼀个圆与超平⾯y=4相交，所以需要跳到(5,4)的左⼦空间去 搜索。所以要将(2,3)加⼊到search_path中，现在search_path中的结点为<(7,2),(2, 3)>；另外，(5,4)与(2,4.5)的距离为 3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
回溯⾄(2,3)，(2,3)是叶⼦节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)， dist更新为(1.5)
回溯⾄(7,2)，同理，以(2,4.5)为圆⼼，以dist=1.5为半径画⼀个圆并不和超平⾯x=7相交, 所以不⽤跳到结点(7,2)的右⼦ 空间去搜索。
⾄此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

6. 鸢尾花种类预测

https://blog.csdn.net/qq_39759664/article/details/123459250

7.特征工程—特征预处理

https://blog.csdn.net/qq_39759664/article/details/123459848

8. 鸢尾花种类预测—流程实现

https://blog.csdn.net/qq_39759664/article/details/123461741

9. 交叉验证，⽹格搜索

https://blog.csdn.net/qq_39759664/article/details/123462661

10.预测facebook签到位置

https://blog.csdn.net/qq_39759664/article/details/123469674

11. 数据分割

通常我们假设测试样本也是从样本真实分布中独⽴同分布采样⽽得。但需注意的是，测试集应该尽可能与训练集互斥。

互斥，即测试样本尽量不在训练集中出现、未在训练过程中使⽤过。

测试样本为什么要尽可能不出现在训练集中呢？为理解这⼀点，不妨考虑这样⼀个场景:。

⽼师出了10道习题供同学们练习，考试时⽼师⼜⽤同样的这10道题作为试题，这个考试成绩能否有效反映出同学 们学得好不好呢？
答案是否定的，可能有的同学只会做这10道题却能得⾼分。

通过对D进⾏适当的处理，从中产⽣出训练集S和测试集T

• 留出法
• 交叉验证法
• ⾃助法

11.1 留出法

“留出法”(hold-out)直接将数据集D划分为两个互斥的集合，其中⼀个集合作为训练集S，另⼀个作为测试集T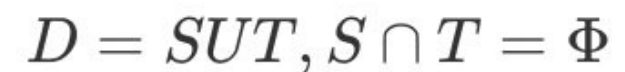
在S上训练出模型后，⽤T来评估其测试误差，作为对 泛化误差的估计。

需注意的是，训练/测试集的划分要尽可能保持数据分布的⼀致性，避免因数据划分过程引⼊额 外的偏差⽽对最终结果产⽣影响，例如在分类任务中⾄少要保持样本的类别⽐例相似。
如果从采样( sampling)的⻆度来看待数据集的划分过程，则保留类别⽐例的采样⽅式通常称为“分层采样”( stratified sampling)。

例如通过对D进⾏分层样⽽获得含70%样本的训练集S和含30%样本的测试集T，
    若D包含500个正例、500个反例，则分层采样得到的S应包含350个正例、
    350个反例，⽽T则包含150个正例和 150个反例；
    若S、T中样本类别⽐例差别很⼤，则误差估计将由于训练/测试数据分布的差异⽽产⽣偏差。
1
2
3
4

另⼀个需注意的问题是，即便在给定训练测试集的样本⽐例后，仍存在多种划分⽅式对初始数据集D进⾏分割。 例如在上⾯的例⼦中，可以把D中的样本排序，然后把前350个正例放到训练集中，也可以把最后350个正例放到训练集 中，这些不同的划分将导致不同的训练/测试集，相应的，模型评估的结果也会有差别。
因此，单次使⽤留出法得到的估计结果往往不够稳定可靠，在使⽤留出法时，⼀般要采⽤若⼲次随机划分、重复进⾏实 验评估后取平均值作为留出法的评估结果。

此外，我们希望评估的是⽤D训练出的模型的性能，但留出法需划分训练/测试集，这就会导致⼀个窘境:

• 若令训练集S包含绝⼤多数样本，则训练出的模型可能更接近于⽤D训练出的模型，但由于T⽐较⼩，评估结果可能 不够稳定准确；
• 若令测试集T多包含⼀些样本，则训练集S与D差别更⼤了，被评估的模型与⽤D训练出的模型相⽐可能有较⼤差 别，从⽽降低了评估结果的保真性( fidelity)。

from sklearn.model_selection
 import train_test_split
  #使⽤train_test_split划分训练集和测试集
   train_X , test_X, train_Y ,test_Y = train_test_split( X, Y, test_size=0.2,random_state=0)
1
2
3
4

11.2 留一法

留⼀法( Leave-One-Out，简称LOO），即每次抽取⼀个样本做为测试集。 显然，留⼀法不受随机样本划分⽅式的影响，因为m个样本只有唯⼀的⽅式划分为m个⼦集⼀每个⼦集包含个样本； 使⽤Python实现留⼀法：

import numpy as np
from sklearn.model_selection import LeaveOneOut,KFold,StratifiedKFold

#留一法
 data=[1,2,3,4]
 loo=LeaveOneOut()
 for train,test in loo.split(data):
     print("%s,%s" % (train,test))
1
2
3
4
5
6
7
8

留⼀法优缺点：

• 优点：留⼀法使⽤的训练集与初始数据集相⽐只少了⼀个样本，这就使得在绝⼤多数情况下，留⼀法中被实际评估的模型 与期望评估的⽤D训练出的模型很相似。因此，留⼀法的评估结果往往被认为⽐较准确。
• 缺点：留⼀法也有其缺陷:在数据集⽐较⼤时，训练m个模型的计算开销可能是难以忍受的(例如数据集包含1百万个样本， 则需训练1百万个模型，⽽这还是在未考虑算法调参的情况下。

11.3 交叉验证法

“交叉验证法”( cross validation)先将数据集D划分为k个⼤⼩相似的互斥⼦集，每个⼦集Di都尽可能保持数据分布的⼀致性，即从D中通过分层抽样得到。
然后，每次⽤k-1个⼦集的并集作为训练集，余下的那个⼦集作为测试集；这样就可获得k组训练/测试集，从⽽可进⾏k 次训练和测试，最终返回的是这k个测试结果的均值。
显然，交叉验证法评估结果的稳定性和保真性在很⼤程度上取决于k的取值，为强调这⼀点，通常把交叉验证法称为“k 折交叉验证”(k- fold cross validation)。k最常⽤的取值是10，此时称为10折交叉验证；其他常⽤的k值有5、20等。下图 给出了10折交叉验证的示意图。

与留出法相似，将数据集D划分为k个⼦集同样存在多种划分⽅式。为减⼩因样本划分不同⽽引⼊的差别，k折交叉验证 通常要随机使⽤不同的划分重复p次，最终的评估结果是这p次k折交叉验证结果的均值，例如常⻅的有 “10次10折交叉 验证”。
交叉验证实现⽅法，除了咱们前⾯讲的GridSearchCV之外，还有KFold, StratifiedKFold
KFold和StratifiedKFold

from sklearn.model_selection import KFold,StratifiedKFold
1

• ⽤法：
  • 将训练/测试数据集划分n_splits个互斥⼦集，每次⽤其中⼀个⼦集当作验证集，剩下的n_splits-1个作为训练 集，进⾏n_splits次训练和测试，得到n_splits个结果
  • StratifiedKFold的⽤法和KFold的区别是：SKFold是分层采样，确保训练集，测试集中，各类别样本的⽐例是 和原始数据集中的⼀致。
• 注意点：对于不能均等分数据集，其前n_samples % n_splits⼦集拥有n_samples // n_splits + 1个样本，其余⼦集都只 有n_samples // n_splits样本
• 参数说明：
  • n_splits：表示划分⼏等份
  • shuffle：在每次划分时，是否进⾏洗牌
    • ①若为Falses时，其效果等同于random_state等于整数，每次划分的结果相同
    • ②若为True时，每次划分的结果都不⼀样，表示经过洗牌，随机取样的

import numpy as np
from sklearn.model_selection import LeaveOneOut,KFold,StratifiedKFold

#留一法
# data=[1,2,3,4]
# loo=LeaveOneOut()
# for train,test in loo.split(data):
#     print("%s,%s" % (train,test))


#交叉验证---KFlod StratifiedKFold
X = np.array([
    [1,2,3,4],
    [11,12,13,14],
    [21,22,23,24],
    [31,32,33,34],
    [41,42,43,44],
    [51,52,53,54],
    [61,62,63,64],
    [71,72,73,74]])
y = np.array([1,1,0,0,1,1,0,0])
folder=KFold(n_splits=4,random_state=None,shuffle=False)
sfolder=StratifiedKFold(n_splits=4,random_state=None,shuffle=False)


#KFold:
print("KFold的结果：")
for train,test in folder.split(X,y):
    print("train:%s,test:%s"% (train,test))

#StratifiedKFold:
print("StratifiedKFold的结果：")
for train,test in sfolder.split(X,y):
    print("train:%s,test:%s"% (train,test))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

11.4 ⾃助法

我们希望评估的是⽤D训练出的模型。但在留出法和交叉验证法中，由于保留了⼀部分样本⽤于测试，因此实际评估的 模型所使⽤的训练集⽐D⼩，这必然会引⼊⼀些因训练样本规模不同⽽导致的估计偏差。留⼀法受训练样本规模变化的 影响较⼩，但计算复杂度⼜太⾼了。

“⾃助法”( bootstrapping)是⼀个⽐较好的解决⽅案，它直接以⾃助采样法( bootstrap sampling)为基础。给定包含m个 样本的数据集D，我们对它进⾏采样产⽣数据集D:

• 每次随机从D中挑选⼀个样本，将其拷⻉放⼊D，然后再将该样本放回初始数据集D中，使得该样本在下次采样时仍 有可能被到；
• 这个过程重复执⾏m次后，我们就得到了包含m个样本的数据集D′，这就是⾃助采样的结果。
  显然，D中有⼀部分样本会在D′中多次出现，⽽另⼀部分样本不出现。可以做⼀个简单的估计，样本在m次采样中始终 不被采到的概率是
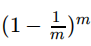  ，取极限得到
  
  即通过⾃助采样，初始数据集D中约有36.8%的样本未出现在采样数据集D′中。
  于是我们可将D′⽤作训练集，D\D′⽤作测试集；这样，实际评估的模型与期望评估的模型都使⽤m个训练样本，⽽我们 仍有数据总量约1/3的、没在训练集中出现的样本⽤于测试。
  这样的测试结果，亦称“包外估计”(out- of-bagestimate）

⾃助法优缺点：

• 优点：
  • ⾃助法在数据集较⼩、难以有效划分训练/测试集时很有⽤；
  • 此外，⾃助法能从初始数据集中产⽣多个不同的训练集，这对集成学习等⽅法有很⼤的好处。
• 缺点：⾃助法产⽣的数据集改变了初始数据集的分布，这会引⼊估计偏差。因此，在初始数据量⾜够时；留出法和交 叉验证法更常⽤⼀些。