概率笔记9——大数定律_0到9出现规律公式

　在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。

　　当我们掷一枚硬币时，说正面朝上的概率是1/2，是这样吗？当你掷十次硬币时，正面朝上的概率可未必是1/2，这个结果带有很强的随机性，并没有什么规律可言。但是当投掷的次数足够多时，规律就呈现出来了。概率研究的是随机现象背后的客观规律，当试验次数趋近于无穷时，正面朝上的频率收敛于1/2概率。

　　大数定律是概率论中讨论随机变量序列的算术平均值向随机变量各数学期望的算术平均值收敛的定律。我觉得还是不要计较概念，关注实际例子就好。

　　以斗地主为例，玩家的水平有高有低，但每个人都有一个真实水平，衡量真实水平的数字特征就是获胜的数学期望。然而高手也不见得每次都会获胜，因为除了实力外，运气也占有很大比重，顶尖高手面对一手烂牌也会束手无策。我们并不能以一局的输赢判断某个人打牌的水平高低，此时运气带来的影响会放大，也就是随机性太大，但是随着打牌的次数增多，高手的成绩会渐渐趋于稳定，他赢的次数会渐渐符合他的真实水平，此时随机性背后的客观规律会逐渐显现出来。

　　我们用一段程序模拟大数定律。这段程序在1~10中随便抽取n个数，然后计算平均值：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
 
results = []
for n in range(1, 10000):
    nums = np.random.randint(low=1, high=10, size=n)
    results.append(nums.mean())
 
df = pd.DataFrame({'均值': results})
df.plot()
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xlabel('样本数量')
plt.ylabel('样本均值')
plt.show()

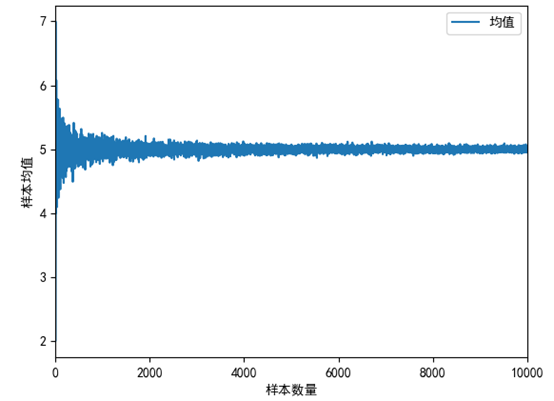
可以看到，随着样本的增多，均值逐渐趋近于平稳，随机性对均值的影响也越来越小。

 

　　以下内容是从 保险不是碰运气(大数法则) （https://www.jianshu.com/p/f384357a554d）上抄来的：

　　根据以往的经验，某类汽车每年的损失概率约为2‰，相应的，在收保费时也会按这个损失比例收取。这时，我们可以把一投保的该类汽车看作一次抛硬币或一次掷骰子，如果投保的汽车数量很少，则相当于抛硬币和掷骰子实验中抛掷的次数很少，那么投保的汽车实际发生事故几率与预先估计的2‰，这个比例可能相差较远，对于保险公司而言则容易发生赔付危机；相反，如果有许许多多的车辆投保该保险，就相当于上面实验中抛掷次数相当多，那么实际的事故发生状况当然就会更接近保险公司估计的2‰，这一损失比例，保险公司就不会担心发生赔付危机了。

　　大数定律的实质就在于，通过集合众多性质相同或相近的风险，把单个风险的不确定性变成集体风险的可测性，从而达到分散风险的目的。其实，一家保险公司承保的业务再少，也可以通过再保险制度将全世界的同类业务联系起来，也符合大数定律的要求。

　　有了大数定律这一科学原理，保险公司在保证大量标的存在的前提下，可以预先估计来年将会发生多少事故，并提前做好准备。所以，不用担心，保险公司是真的很“保险”，并不是在碰运气。

 

---

　　作者：我是8位的

       出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公作者众号“我是8位的”