[足式机器人]Part2 Dr. CAN学习笔记-Ch00-2 - 数学知识基础

本文仅供学习使用
本文参考：
B站：DR_CAN
《控制之美(卷1)》 王天威
《控制之美(卷2)》 王天威

4. Ch0-4 线性时不变系统中的冲激响应与卷积

4.1 LIT System：Linear Time Invariant

• 运算operator : O { ⋅ } O\left\{ \cdot \right\} O{ ⋅}
  I n p u t O { f ( t ) } = o u t p u t x ( t ) $$\begin{array}{c} Input\\ O\left\{ f\left( t \right) \right\}\\ \end{array}$$ = $$\begin{array}{c} output\\ x\left( t \right)\\ \end{array}$$ InputO{ f(t)}​=outputx(t)​

• 线性——叠加原理superpositin principle：
  { O { f 1 ( t ) + f 2 ( t ) } = x 1 ( t ) + x 2 ( t ) O { a f 1 ( t ) } = a x 1 ( t ) O { a 1 f 1 ( t ) + a 2 f 2 ( t ) } = a 1 x 1 ( t ) + a 2 x 2 ( t ) $$\begin{cases} O\left\{ f_1\left( t \right) +f_2\left( t \right) \right\} =x_1\left( t \right) +x_2\left( t \right)\\ O\left\{ af_1\left( t \right) \right\} =ax_1\left( t \right)\\ O\left\{ a_1f_1\left( t \right) +a_2f_2\left( t \right) \right\} =a_1x_1\left( t \right) +a_2x_2\left( t \right)\\ \end{cases}$$ ⎩ ⎨ ⎧​O{ f1​(t)+f2​(t)}=x1​(t)+x2​(t)O{ af1​(t)}=ax1​(t)O{ a1​f1​(t)+a2​f2​(t)}=a1​x1​(t)+a2​x2​(t)​

• 时不变Time Invariant：
  O { f ( t ) } = x ( t ) ⇒ O { f ( t − τ ) } = x ( t − τ ) O\left\{ f\left( t \right) \right\} =x\left( t \right) \Rightarrow O\left\{ f\left( t-\tau \right) \right\} =x\left( t-\tau \right) O{ f(t)}=x(t)⇒O{ f(t−τ)}=x(t−τ)

4.2 卷积 Convolution

卷积与微分方程：

• 线性时不变系统的输出与输入之间是卷积的关系
• 单位冲激响应可以完整地描述线性时不变系统。
• 微分方程可以直接描述系统输入与输出之间的卷积关系。

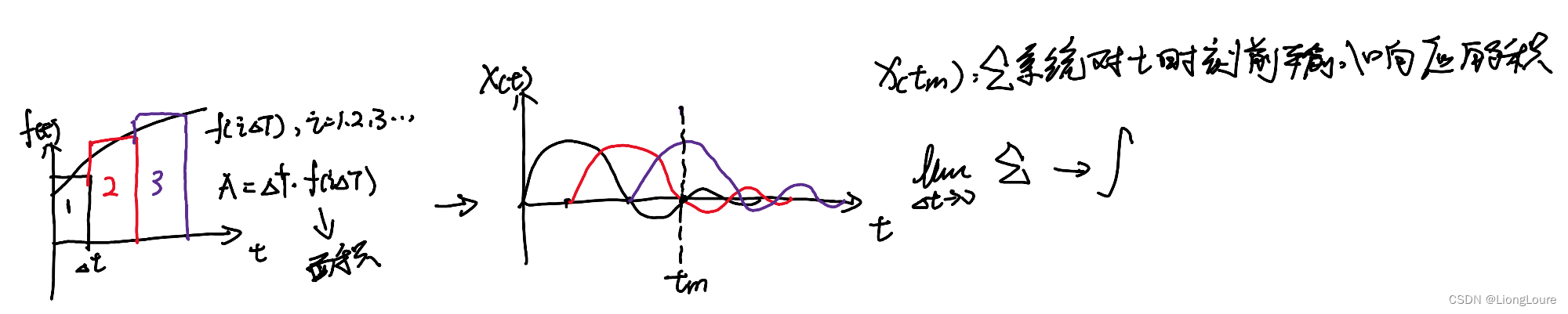
4.3 单位冲激 Unit Impulse——Dirac Delta

单位冲击函数（Unit Impulse），又称为狄拉克函数（Dirac Delta）,是一个宽度为0、面积为1的函数，这是一个纯数学函数

LIT系统，$h(t)$可以完全定义系统， 是系统对于冲激函数δ(t)（mpulse Response） 的冲激响应

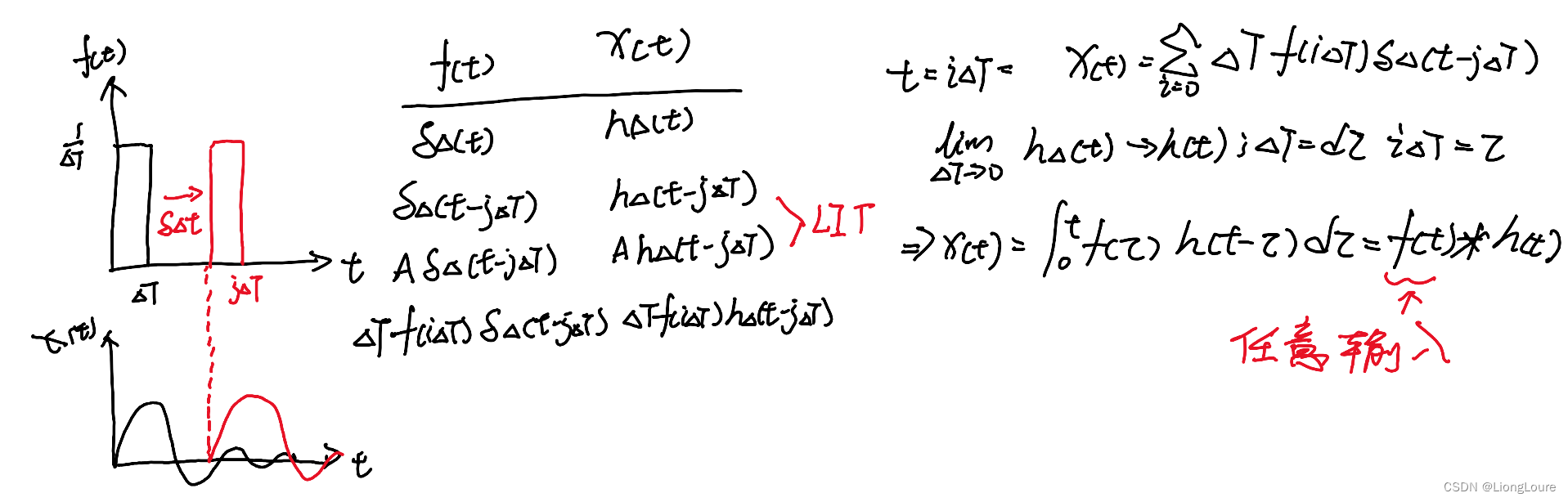
4.4 LIT 线性时不变系统状态空间方程的解

状态空间方程是指将系统描述为一组关于状态和输人的微分方程以及代表输出的代数方程的形式。
$$\begin{gathered} \frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}=Ax\left(t\right)+Bu\left(t\right) \\ y\left(t\right)=Cx\left(t\right)+Du\left(t\right) \end{gathered}$$
$A$是一个$n\times n$ 矩阵,表示系统状态变量之间的关系,称为状态矩阵或者系统矩阵。
$B$ 是一个$n\times p$ 矩阵,表示输人对状态量的影响,称为输入矩阵或者控制矩阵。
$C$ 是一个$m\times n$ 矩阵,表示系统的输出与系统状态变量的关系,称为输出矩阵。
$D$ 是一个$m\times p$ 矩阵,表示系统的输人直接作用在系统输出的部分，称为直接传递矩阵。

结合前面的分析可以发现，当矩阵$A$的特征值实部部分都小于0时,状态转移矩阵$e^{A(t-t_0)}$将随着时间的增加趋向于0,这是系统稳定性分析的基础。

对于时变系统,在一般情况下不容易找到解析解,多采用数值求解的方法,这不在本书的讨论范围之内。

5. Ch0-5 Laplace Transform of Convolution卷积的拉普拉斯变换

线性时不变系统 ： LIT System
冲激响应：Impluse Response
卷积：Convolution

Laplace Transform : $X\left(s\right)=\mathcal{L}\left[x\left(t\right)\right]={\int }_0^{\infty }x\left(t\right)e^{-st}\mathrm{d}t$

Convolution : $x\left(t\right)\ast g\left(t\right)={\int }_0^{t}x\left(\tau \right)g\left(t-\tau \right)\mathrm{d}\tau$

证明：$\mathcal{L}[x\left(t\right)\ast g$