二叉树链式结构(入门)_二叉链树

目录

一.二叉树的简单构建

二.二叉树的遍历

1.先序遍历

2.中序遍历

3.后序遍历

4.已知先序，中序，构建一颗二叉树

5.层序遍历

三.有关二叉树的简单oj题

1.二叉树节点个数

2.二叉树叶子节点个数

3.二叉树第k层节点个数

4.求二叉树的高度

5.二叉树查找值为x的节点

6.单值二叉树

7.检查两棵树是否相同

8.另一棵树的子树

9.翻转二叉树

10.对称二叉树

11.判断二叉树是否为一棵平衡二叉树

12.二叉树的构建

13.判断二叉树是否为一棵完全二叉树 

14.二叉树的销毁

15.二叉树的先序遍历/中序遍历/后序遍历

---

一.二叉树的简单构建

如下图所示，是一棵我们常见的链式二叉树.

不同于链表，二叉树每个结点并不是单一链接的，而是分别指向两个不同的结点.

即结点结构里面，存储有left,right两个指针.

将结点转化成对应的C语言代码如下:

typedef int BTDataType;
 
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

 如果想要迅速手动构建一棵二叉树，我们只要实现相应创建单个结点的函数.然后再手动按照我们

的想法自己链接起来即可.

//创建单个结点
BTNode* BuyBTNode(BTDataType x)
{
	//给单个结点开辟空间
    BTNode* tmp = (BTNode*)malloc(sizeof(BTNode));
    //判断是否申请空间成功
	if (tmp == NULL)
	{
		perror("malloc fail.\n");
		exit(-1);
	}
    //赋值
	tmp->data = x;
	tmp->left = tmp->right = NULL;
	return tmp;
}

 比方说我们想要构建上面这棵这棵树.

确定好每个结点的名字后，直接手动链接即可.

int main()
{
    BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(3);
	BTNode* n3 = BuyBTNode(5);
	BTNode* n4 = BuyBTNode(9);
	BTNode* n5 = BuyBTNode(11);
	BTNode* n6 = BuyBTNode(2);
 
	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n2->right = n5;
	n3->right = n6;
    return 0;
}

 当然这并非二叉树真正构建的方法，但我们可以通过这个方法，迅速构建出我们想要的二叉树.

在进一步了解二叉树之前，我们还需要换种角度看待二叉树的结构.

假如把空，也看作是一个结点的话

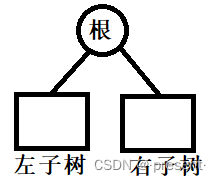
我们可以发现，任何一棵树，都可以看作是  根+左子树+右子树的结构

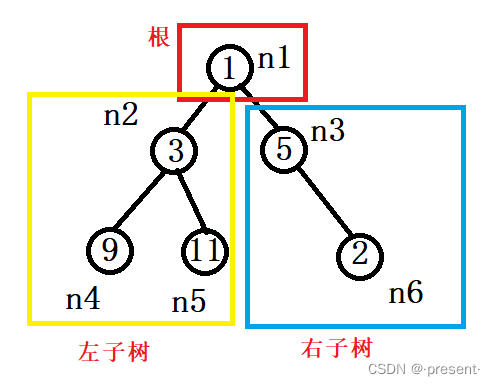
 同样的，左子树也是一棵树，因此它也依旧可以看作  根+左子树+右子树的结构

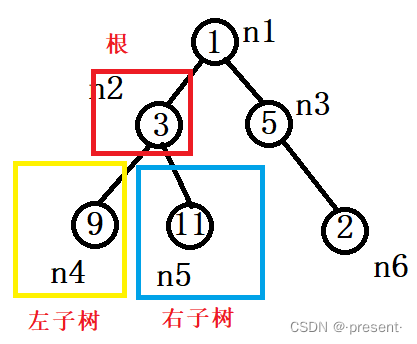
甚至一个结点也是一棵树，它也依旧可以看作 根+左子树+右子树的结构

只不过它的左子树和右子树都是空.

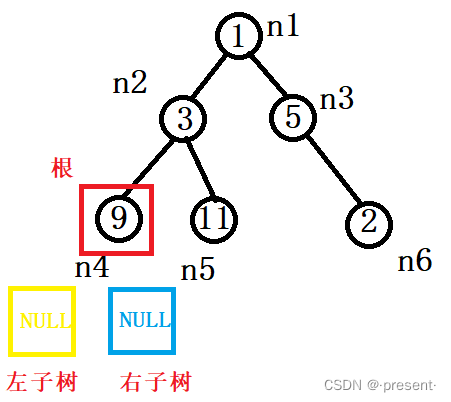
从这里我们也可以看出二叉树的结构特点:

每一个最小的单元，到组合成一个更大的单元，都有着相似的结构.

因此，我们也可以猜想到，二叉树和递归之间的关系是密不可分的.

而将二叉树看作三个基本单元：根节点，左子树，右子树组成，也被称之为二叉树的递归定义.

二.二叉树的遍历

由于二叉树的形状是不确定的，甚至可以全部倾向一边，构成我们熟悉的单链表.

因此，从某种意义上来说，二叉树的增删查改并没有意义，除非有着特殊结构的限定.

与此相反，二叉树的遍历问题有着重要的地位，后面很多题目的求解，其实或多或少，都借鉴了遍

历问题的思想.

那什么是遍历问题呢?

通俗点讲，就是按照什么样的搜索路径巡访树中的每个结点，使得每个结点有且仅被访问一次.

实际上，递归的过程是相同的，唯一不同的是，访问结点的时机.

1.先序遍历

假如按照根结点，再左子树，最后右子树的顺序访问，我们称之为先序遍历.

结合下面的例子，就是先访问根节点n1，再访问其左子树,对于左子树来说，n2又是它的根节点.

以此类推，假如按照先序遍历来打印这棵树，得到的结果是

其代码的实现，在理解递归和其思想后，也比较容易实现

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	//递归返回条件
    if (root == NULL)
		return;
    //打印根节点
	printf("%d ", root->data);
    //递归访问左子树
	BinaryTreePrevOrder(root->left);
    //递归访问右子树
	BinaryTreePrevOrder(root->right);
}

2.中序遍历

同理，假如按照先左子树，再根节点，最后右子树的顺序，我们称之为中序遍历

结合下面的例子，就是先访问n1的左子树，然后访问n2的左子树，一直到访问n4的左子树，遇到

空指针，返回,打印n2的左子树n4,然后才打印n2(根)，最后递归调用，访问n2的右子树n5.

以此类推，假如按照中序遍历来打印这棵树，得到的结果是

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	//递归返回条件
    if (root == NULL)
		return;
    //中序遍历左子树
	BinaryTreeInOrder(root->left);
    //访问根结点
	printf("%d ", root->data);
    //中序遍历右子树
	BinaryTreeInOrder(root->right);
}

3.后序遍历

类似，先左子树，后右子树，最后才访问根节点的顺序，我们称之为后序遍历

结合下面的例子，就是先访问n1的左子树，递归访问n2的左子树，紧接着访问n4的左子树，为空

返回，访问n4的右子树,也为空，返回.这个时候才打印n4(根)

以此类推，假如按照后序遍历来打印这棵树，得到的结果是

void BinaryTreePostOrder(BTNode* root)
{
	//递归返回条件
    if (root == NULL)
		return;
    //递归后序遍历左子树
	BinaryTreePostOrder(root->left);
    //递归后序遍历右子树
	BinaryTreePostOrder(root->right);
    //访问根节点
	printf("%d ", root->data);
}

4.已知先序，中序，构建一颗二叉树

我们经常会遇到类似这样的问题，假如知道前序遍历序列，中序遍历序列，如何得到后序遍历序列

呢？

我们知道先序遍历，是按照根，左子树，右子树顺序访问一棵树的. 

那先序遍历，得到的第一个值，这里是5，肯定就是整棵树的根.

我们又知道中序遍历，是按照左子树，根，右子树顺序访问一棵树的

那我们知道根是5后，自然就可以把中序遍历划分为下面的结构.

 我们再看左子树4  7，在先序遍历时，得到的第一个值，一定是树的根.

那结合先序遍历，我们就可以知道，左子树的根是7，再看回中序遍历，4在7的左边，因此4是7的

左子树.这样我们就可以复原出原本这棵树的样子.

 

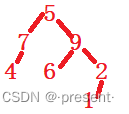
得到树原本的逻辑结构，得到后序遍历也就很轻松了.

最后答案是  4  7  6  1  2  9  5.

类似的，我们知道中序遍历，后序遍历，也可以确定一棵二叉树.

但值得注意的是，只知道先序，后序序列,是无法确定一棵树的.

理由也很简单，没有中序遍历，我们无法进一步划分左子树，右子树的形状是如何的，先序和后序

仅仅为我们提供了根的位置.

单拿上面的例子来看

上述两棵树都可以得到相同的先序，后序序列，但它们中序遍历的结果却是不同的. 

5.层序遍历

除了上述的按先序，中序，后序遍历一棵二叉树，还可以从上到下，从左到右按层次遍历，我们称

之为层序遍历.

对于原本我们的例子来说，就是一层一层从左到右访问，先访问n1，然后访问n2，再访问n3

以此类推，直到访问一棵树所有的结点为止.得到的结果如下:

而不同于前面遍历实现的思想，我们需要借助队列来实现层序遍历.

每个结点入列后，在出列的同时，我们把与它相链接非空的结点，也一并入列.

队列的先进先出结构，也保证了一层层访问结点.

具体来说，我们先把n1入列.

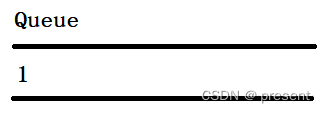
访问n1时，n1需要出列，同时我们把和1相链接的两个结点n2,n3入列. 

同理，访问n2时，n2需要出列，同时我们把n4,n5两个结点入列.

以此类推，我们就可以实现层序遍历.

有关C语言队列的实现，具体可以参照之前相关的文章.

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
    //如果根结点不为空，就先让其入列
	if (root)
		QueuePush(&q, root);
    //不断有元素出列，直到队列为空才停止
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->data);
		QueuePop(&q);
		//如果左孩子不为空
		if (front->left)
	     	QueuePush(&q, front->left);
		//如果右孩子不为空
		if (front->right)
            QueuePush(&q, front->right);
	}
	printf("\n");
	QueueDestroy(&q);
}

 leetcode也有二叉树遍历的题目，不过由于C语言没有STL库，队列这种数据结构需要我们自己构

造，会导致C语言实现起来会比较麻烦.

//题目描述种限定节点只有2000个
#define MAX_SUM 2000
typedef struct TreeNode* QDataType;
typedef struct QueueNode {
    QDataType data;
    struct QueueNode* next;
}QNode;
typedef struct Queue {
    QNode* head;
    QNode* rear;
    int size;
}Queue;
void QueueInit(Queue* ps)
{
    ps->head = ps->rear = NULL;
    ps->size = 0;
}
void DestroyQueue(Queue* ps)
{
    QNode* cur = ps->head;
    while (cur)
    {
        QNode* next = cur->next;
        free(cur);
        cur = next;
    }
    ps->head = ps->rear = NULL;
    ps->size = 0;
}
bool QueueEmpty(Queue* ps)
{
    return ps->head == NULL && ps->rear == NULL;
}
void QueuePush(Queue* ps, QDataType x)
{
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    newnode->data = x;
    newnode->next = NULL;
    if (ps->head == NULL)
    {
        ps->head = ps->rear = newnode;
    }
    else
    {
        ps->rear->next = newnode;
        ps->rear = newnode;
    }
    ps->size++;
}
void QueuePop(Queue* ps)
{
    if (!QueueEmpty(ps))
    {
        if (ps->head->next == NULL)
        {
            free(ps->head);
            ps->head = ps->rear = NULL;
        }
        else
        {
            QNode* del = ps->head;
            ps->head = ps->head->next;
            free(del);
        }
        ps->size--;
    }
}
 
QDataType QueueFront(Queue* ps)
{
    return ps->head->data;
}
 
int QueueSize(Queue* ps)
{
    return ps->size;
}
 
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
     //根节点是空指针，直接返回NULL
     if (!root)
     {
         *returnSize = 0;
         return NULL;
     }
     //构造一个二维数组
     int** a = (int**)malloc(sizeof(int*)*MAX_SUM);
     //创建一个队列，队列此时每个元素类型是Struct TreeNode
     Queue q;
     QueueInit(&q);
     QueuePush(&q,root);
     int returncnt = 0;
     //记录每一列有多少元素的数组
     int *column =(int *)malloc(sizeof(int)*MAX_SUM);
     //如果队列不为空
     while (!QueueEmpty(&q))
     {    
          //判断第几层有几个元素(队列长度)
          int sz = QueueSize(&q);
          //二维数组指向相应动态数组
          a[returncnt] = (int*)malloc(sizeof(int)*sz);
          // 记录不同列有多少个元素
          column[returncnt] = sz;
          // 每一层有多少元素，就循环多少次，赋值相应多少元素
          for (int i = 0;i < sz;++i)
          {   
            //取出队列元素
            struct TreeNode* node = QueueFront(&q);
            a[returncnt][i] = node->val;
            //相应节点的左孩子和右孩子入列,左孩子和右孩子不为空才入列
            if (node->left)
                QueuePush(&q,node->left);
            if (node->right)
                QueuePush(&q,node->right);
            //左孩子和右孩子都入列后，节点才出列
            QueuePop(&q);
          }
          returncnt++; 
     }
     *returnSize= returncnt;
     *returnColumnSizes = column;
     DestroyQueue(&q);
     return a;
}

三.有关二叉树的简单oj题

为了加深对链式二叉树和递归相关知识点的理解，我们可以尝试入手几道简单的题目来加深印象.

1.二叉树节点个数

依旧拿我们先前那棵树做例子，我们如何得到这棵树有多少个节点呢？

我们直到，递归的思想，就是将大问题，转化成小问题进行解决.

依旧是抽象出树的递归结构，我们怎么得到它的节点呢? 

一个简单的思路，就是假如我们得到左子树的节点个数，又得到右子树的节点个数，再加上1(根节

点)，那总的节点个数 = 左子树的节点个数 + 右子树的节点个数  + 1.

假设是空子树，则返回0，于是我们便有了实现该题的思路.

// 二叉树节点个数
//法一
int BinaryTreeSize(BTNode* root)
{
	//递归返回条件，遇到空树，返回0
    if (root == NULL)
		return 0;
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
 
//法二:用三目运算符简化程序
int BinaryTreeSize(BTNode* root)
{
   	return  root == NULL ? 0:BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

2.二叉树叶子节点个数

对比第一题，难度又加大了一点，这次需要判断叶子节点的个数，叶子节点就是没有孩子的节点.

我们又该如何解决这个问题呢?

叶子节点的特点就是没有孩子，在程序中对应，left和right指针都为空.

一棵树叶子节点 = 左子树叶子节点个数 + 右子树叶子节点个数

同样，假设是空子树，则返回0，我们便有了实现该题的思路.

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	//递归返回条件，根节点为空
    if (root == NULL)
		return 0;
    //left和right指针都为空，则说明是一个叶子节点
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

3.二叉树第k层节点个数

在第二题基础上，我们又进了一步，这一次需要解决第k层节点的个数.

同样，我们用二叉树的递归结构图来思考.

这里，我们设第1层，为k==1，那树为空的时候，对应的就是k==0（当然也可以设第一层为k==0，但此时空对应k == -1）

那假如我们要求解第1层的节点个数，我们可以自信的说，有1个，也就是一个根节点.

那求解第2层，k == 2时呢?

对于根节点来说，它们是第二层，但假如把它们也看作树，它们就是自己树的根节点，对应的是它

们自己的第一层.

因此，第k层的节点个数 = 将所有第k层节点作为子树时，相应根节点的个数.

//二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	 if (root == NULL)
		 return 0;
     //假如k==1，则说明此时已经到达第k层,可以统计是否存在根节点
	 if (k == 1)
		 return 1;
	 return BinaryTreeLevelKSize(root->left, k - 1)+ BinaryTreeLevelKSize(root->right, k - 1);
}

4.求二叉树的高度

对于下面这棵树，它的树高是4,具体是如何计算出来的呢?

我们可以发现，一棵树的高度 = 左子树和右子树高度较大值 + 1

当遇到空的时候，对应的高度就是0，递归就可以返回.

拿上图举例子，这棵树的高度 = 两棵子树中较大的高度（3）+ 1 == 4

// 求二叉树的树高
int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
    //记录左子树的高度
	int leftheight = BinaryTreeHeight(root->left);
    //记录右子树的高度
	int rightheight = BinaryTreeHeight(root->right);
	return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

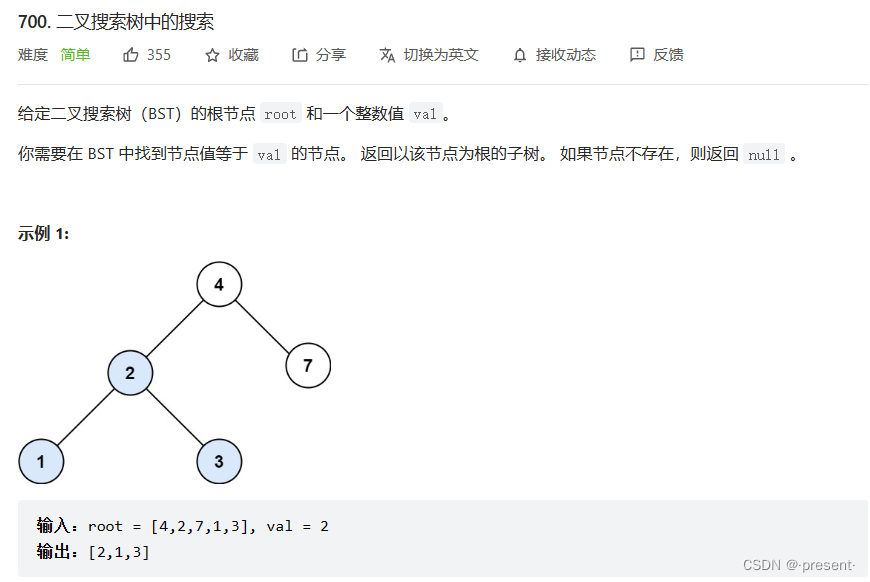
5.二叉树查找值为x的节点

想要找到值为x的节点非常简单，可以转化成去左子树中找，再去右子树中去找的递归小问题.

但问题的关键是如何在递归的程序中，将对应节点的指针返回回来呢?

像第2，3题中，直接最后返回，显然不太现实，指针做加减不符合我们的要求，利用与或等等运算

也不是我们想要的，我们需要具体的指针的值.

这里我们借鉴第4题的思路，将指针的值，保存下来，如果不为空，则返回回来.

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
    //如果root->data == x,则说明找到该节点，返回对应指针
	if (root->data == x)
		return root;
    
    //递归去左子树中找，无论是否找到，都将指针保存下来
	BTNode* ret1 = BinaryTreeFind(root->left, x);
    //指针不为空，则层层返回
	if (ret1)
		return ret1;
    //递归去右子树中找，无论是否找到，都将指针保存下来
	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;
    //左子树和右子树中都没有，则返回空，代表不存在该节点
	return NULL;
}

6.单值二叉树

题目描述如下:

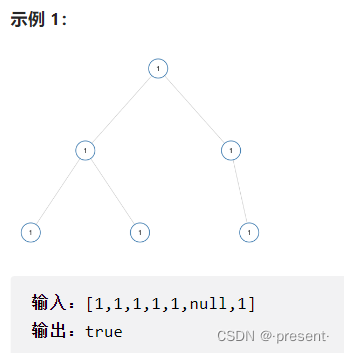
 很多人做这道题的时候，会把它分解为左子树，根，右子树三者的值是否相等的子问题.

但是卡在了如何将判断的值返回出去的问题上

但我们还需要注意一点，实际上并没有必要这样判断，毕竟有可能左子树为空，右子树也可能为

空，这需要判断的东西实际上非常多.

正确的思路是，当左子树不为空的时候，先判断左子树的值和根节点的的值是否相等，不相等，则

绝对不可能是一棵单值二叉树.

当左子树满足的情况下，再判断右子树和根节点的值是否相等.

bool isUnivalTree(struct TreeNode* root){
    if (root == NULL)
      return true;
    //判断左子树和根节点是否相等
    if (root->left && root->left->val != root->val)
        return false;
    //判断右子树和根节点是否相等
    if (root->right && root->right->val != root->val)
        return false;
    //递归调用判断左子树和右子树是否分别是一棵单值二叉树
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

7.检查两棵树是否相同

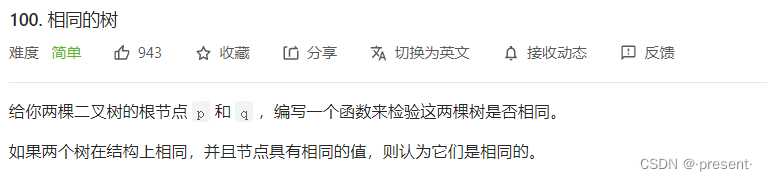
有了前面题目的思路，判断两棵树是否相等，实际上就是转化为递归判断它们的左子树和右子树分

别是否相同. 

那对于一棵足够小的树，如何判断它们是否相等呢?

经过思考，我们可以将其划分为3个阶段进行判断:

1.假如两棵树都是空，那两者肯定是相同的.

2.假如一棵树为空，另一棵树不为空，那两者肯定不相同

3.假如两棵树都不为空，那对应的根节点分别进行判断就好.

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
     if (p == NULL && q == NULL)
       return true;
     //p与q中有一个为空
     if (p == NULL || q == NULL)
        return false;
     if (p->val != q->val)
        return false;
    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

8.另一棵树的子树

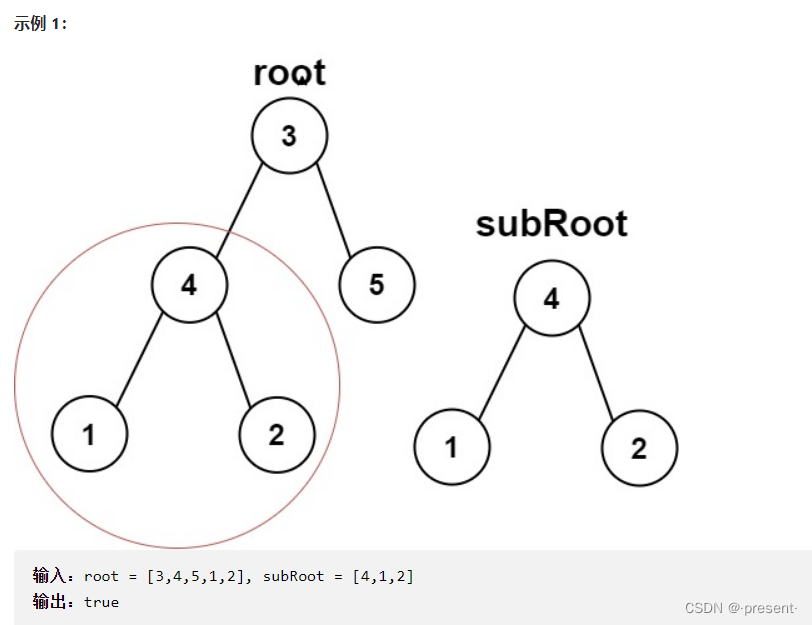
 题目有两点需要我们注意的，子树为一个节点时，或者和原树相同，也都属于原树的子树.

一个简单解决这道题的思路是，调用我们前面实现过的判断两棵树是否为相同的树的函数.

只要遍历原树的每一个节点，和子树进行判断是否为相同的树即可.

bool issameTree(struct TreeNode* r1,struct TreeNode * r2)
{
   if (r1 == NULL && r2 == NULL)
      return true;
   if (r1 == NULL || r2 == NULL)
      return false;
   if (r1->val != r2->val)
      return false;
   return issameTree(r1->left,r2->left) && issameTree(r1->right,r2->right);
}
 
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
     //递归返回，假如节点为空，则返回false，代表不存在子树
     if (root == NULL)
       return false;
     if (issameTree(root,subRoot))
        return true;
     //利用或运算即可，只要找到存在子树，就返回true
     return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

9.翻转二叉树

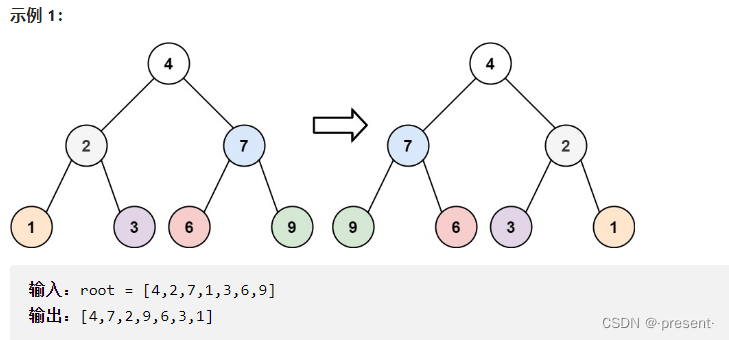
那这道题的思路其实也比较清晰，想要翻转一棵二叉树，那就保存左节点，将左指针指向右节点，

右指针再指向我们保存的左节点即可.

struct TreeNode* invertTree(struct TreeNode* root){
    if (root == NULL)
     return NULL;
    struct TreeNode * tmp = invertTree(root->left);
    root->left = invertTree(root->right);
    root->right = tmp;
    return root;
}

10.对称二叉树

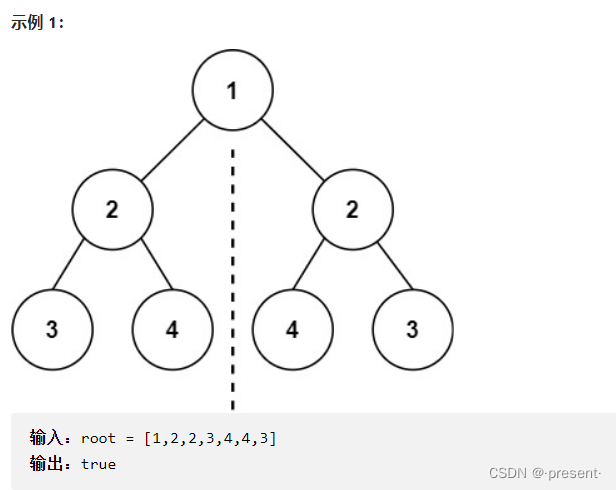
第一个思路是将树翻转过来，再判断是否相同，这固然可以，但关键是改变了原树，那再翻转回来

实际上会比较麻烦. 

其实，和判断两棵二叉树是否相同类似，两棵二叉树是否是对称二叉树.

实际上只需要判断，左子树和右子树是否相等，右子树和左子树又是否相等即可.

判断两棵树是否相同，我们依旧可以照猫画虎将其划分为3个阶段进行判断:

1.假如两棵树都是空，那两者肯定是相同的.

2.假如一棵树为空，另一棵树不为空，那两者肯定不相同

3.假如两棵树都不为空，那对应的根节点分别进行判断就好.

bool isSymmetric_tree(struct TreeNode * p,struct TreeNode * q)
{
     if (p == NULL && q == NULL)
       return true;
     if (p == NULL || q == NULL)
       return false;
     if (p->val != q->val)
       return false;
     //递归判断左子树和右子树，右子树和左子树是否分别相同
     return isSymmetric_tree(p->left,q->right) && isSymmetric_tree(p->right,q->left);
}
 
bool isSymmetric(struct TreeNode* root){
    //假如根节点为空，直接返回false
    return root && isSymmetric_tree(root->left,root->right);
}

11.判断二叉树是否为一棵平衡二叉树

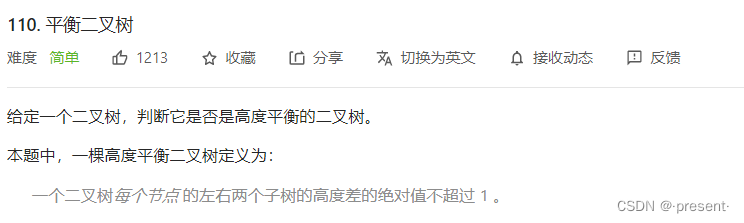
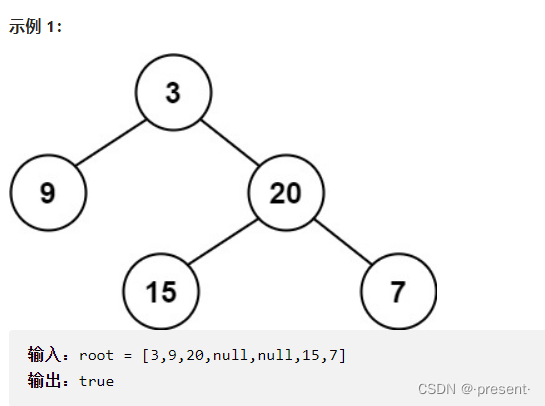
前面我们已经实现过求树的高度，那遍历树的每一个节点，再判断左子树和右子树高度之差是否大

于1即可.

 int TreeHeight(struct TreeNode * root)
 {
     if (root == NULL)
       return 0;
     int leftheight = TreeHeight(root->left);
     int rightheight = TreeHeight(root->right);
     return leftheight > rightheight?leftheight + 1:rightheight + 1;
 }
bool isBalanced(struct TreeNode* root){
    if (root == NULL)
      return true;
    //判断左子树和右子树高度之差是否大于1
    if (fabs(TreeHeight(root->left) - TreeHeight(root->right))>1)
       return false;
    return isBalanced(root->left) && isBalanced(root->right);
}

不过这样的过程，是一个自顶向下的过程，对于下面底层的叶子节点而言，实际上被重复计算过很

多次高度，当为一条链的时候，时间复杂度甚至会达到O(n^2)，这样的效率实际上并不高.

仿照第4题，求解树的高度，我们需要记录下来树高，自底向上来判断，这样就可以大大提高效率.

一旦我们发现子树不是一棵平衡二叉树，则直接返回就好，不需要再进行判断.

int Height(struct TreeNode* root)
{
    //如果树为空，则返回0
    if (root == NULL)
       return 0;
    //及时记录左子树高度
    int leftheight = Height(root->left);
    //记录右子树高度
    int rightheight = Height(root->right);
    //如果左子树或右子树高度有等于-1的，则证明存在子树不是平衡二叉树，直接层层返回
    if (leftheight == -1||rightheight == -1||fabs(rightheight - leftheight) > 1)
       return -1;
    else
       return fmax(rightheight,leftheight)+1;
}
bool isBalanced(struct TreeNode* root){
    return Height(root) >= 0;
}

12.二叉树的构建

有了前面的基础(递归)后,我们就可以尝试学习其中一种构建链式二叉树的方法.

题目难点在于如何根据先序遍历，构建出一棵二叉树，毕竟中序遍历，我们其实前面已经实现过

了,而且难度也比较小.

我们用一个字符数组存储输入数据，遇到"#"，则证明是一个空结点，返回NULL即可.

借鉴先序遍历的思想，只不过这里访问节点，并不是打印数据，而是创建新节点，并赋值.

构建一棵树，只需要创建好根节点，左子树构建好，根节点的left指向左子树，右子树构建好，根

节点的right指向右子树即可.

PS:这里还需要注意，由于我们采取递归的方式构建树，因此我们传递i的时候，应该传指针进去，

这样每次修改值，都是针对同一个i进行修改.

#include <stdio.h>
#include <stdlib.h>
typedef struct BTNode {
	char val;
	struct BTNode* left;
	struct BTNode* right;
}BTNode;
BTNode* CreateTree(char* data, int* pi)
{
	if (data[*pi] == '#')
	{
		//遇到空，返回指针后，数组也要往后移动
		(*pi)++;
		return NULL;
	}
    //创建新节点
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->val = data[(*pi)++];
    //新节点的left，指向构建好的左子树
	node->left = CreateTree(data, pi);
    //新节点的right，指向构建好的右子树
	node->right = CreateTree(data, pi);
	return node;
}
 
void InorderTree(BTNode* root)
{
	if (root == NULL)
		return;
	InorderTree(root->left);
	printf("%c ", root->val);
	InorderTree(root->right);
}
 
int main() {
	char data[100];
	scanf("%s", data);
	int i = 0;
	BTNode* root = CreateTree(data, &i);
	InorderTree(root);
	return 0;
}

13.判断二叉树是否为一棵完全二叉树 

和前面题目思想不同，前面大多是采用递归，将一个大任务，拆分成一个个小任务.

而判断一棵完全二叉树，采用的则是层序遍历的思想.

依旧拿下面的二叉树做例子，我们可以发现，它并不是一棵完全二叉树，因为n5,n6之间，缺了相

应的节点. 

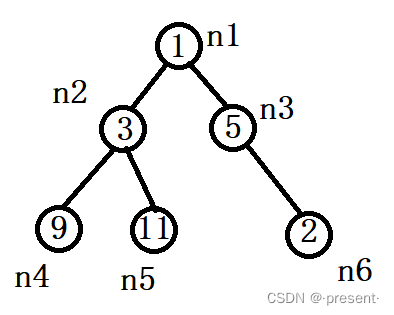
如何表示缺了相应的节点呢?

对应的就是队列遇到了空指针.

于是我们就有了思路：

层序遍历二叉树，不管是否是空节点，每次出列的时候，就把其相链接的节点全部压入队列.

假如队列遇到空指针，则判断队列里面是否还有元素，假如还存在元素，则绝对不是一个完全二叉

树，反之则为一棵完全二叉树.

PS：此时存进去队列的元素，和我们之前的int类型不同，是一个二叉树结点指针.

// 判断二叉树是否是完全二叉树
// 采取层序遍历的思想
bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;
	//创建一个队列
	Queue q;
	QueueInit(&q);
	BTNode* ret = root;
	QueuePush(&q, ret);
	//只要队列不为空
	while (!QueueEmpty(&q))
	{
		BTNode* ret = QueueFront(&q);
		QueuePop(&q);
		//如果ret为空，则循环跳出
		if (!ret)
			break;
		QueuePush(&q, ret->left);
		QueuePush(&q, ret->right);
	}
 
	while (!QueueEmpty(&q))
	{
		BTNode* ret = QueueFront(&q);
		//如果在空指针后，还有不为空的指针,则一定不是一棵完全二叉树
		if (ret)
		{
			QueueDestroy(&q);
			return false;
		}
		QueuePop(&q);
	}
	QueueDestroy(&q);
	return true;
}

14.二叉树的销毁

二叉树的销毁，有三种方式供我们选择，先序，中序，和后序.

但仔细思索后，我们会发现先序和中序其实都不行.

假设我们采用先序遍历销毁二叉树，根节点被free，那它的左子树和右子树，显然我们就再也找不

到.

同理，中序遍历也是如此，我们找不到根节点的右子树.

所以，二叉树的销毁，只能采取后序遍历的方式.

PS:这里并没有采取二级指针的方式，因此，使用该函数的时候，还需要手动将根节点指针置空.

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	//只能采用后序遍历的方式
    //先销毁左子树
	BinaryTreeDestory(root->left);
    //再销毁右子树
	BinaryTreeDestory(root->right);
    //最后释放根节点
	free(root);
}

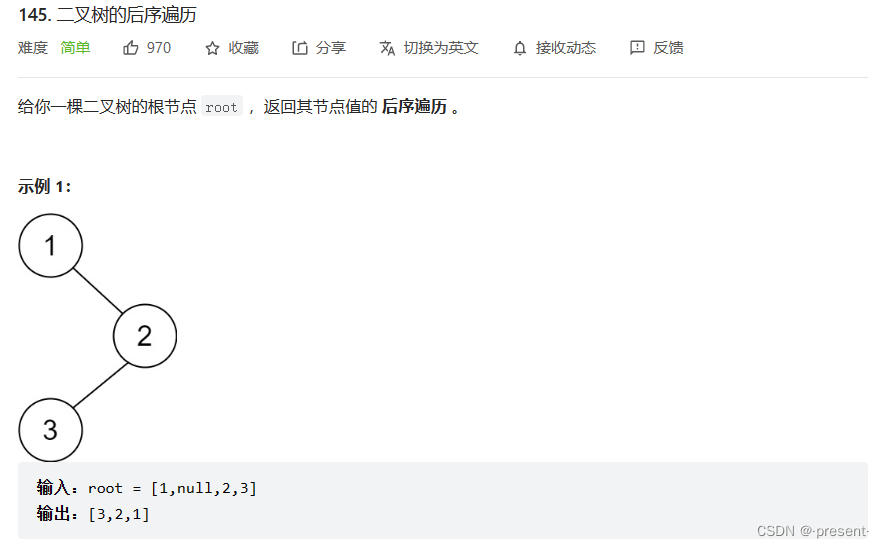
15.二叉树的先序遍历/中序遍历/后序遍历

和我们先前实现的二叉树先序遍历还不同，leetcode的题目，还需要返回开辟数组的大小.

因此，在构建上，我们除了要实现先序遍历构建新数组外，还需要额外构建TreeSize函数.

int TreeSize(struct TreeNode* root)
{
    return root == NULL?0:TreeSize(root->left) + TreeSize(root->right)+1;
}
void Preorder(struct TreeNode* root,int* ret,int* i)
{
    if (root == NULL)
      return;
    ret[(*i)++] = root->val;
    Preorder(root->left,ret,i);
    Preorder(root->right,ret,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    *returnSize = size;
    int* ret = (int* )malloc(sizeof(int)*size);
    int i = 0;
    Preorder(root,ret,&i);
    return ret;
}

中序遍历和后序遍历也是类似的思路，这里不再细讲.

int TreeSize(struct TreeNode* root)
{
    return root == NULL?0:TreeSize(root->left) + TreeSize(root->right)+1;
}
void Inorder(struct TreeNode* root,int* ret,int* i)
{
    if (root == NULL)
      return;
    Inorder(root->left,ret,i);
    ret[(*i)++] = root->val;
    Inorder(root->right,ret,i);
}
//中序遍历
int* inorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    *returnSize = size;
    int* ret = (int* )malloc(sizeof(int)*size);
    int i = 0;
    Inorder(root,ret,&i);
    return ret;
}

int TreeSize(struct TreeNode* root)
{
    return root == NULL?0:TreeSize(root->left) + TreeSize(root->right)+1;
}
void Postorder(struct TreeNode* root,int* ret,int* i)
{
    if (root == NULL)
      return;
    Postorder(root->left,ret,i);
    Postorder(root->right,ret,i);
    ret[(*i)++] = root->val;
}
//后序遍历
int* postorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    *returnSize = size;
    int* ret = (int* )malloc(sizeof(int)*size);
    int i = 0;
    Postorder(root,ret,&i);
    return ret;
}