devbox
繁依Fanyi0
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

选择排序，冒泡排序，插入排序，快速排序及其优化

作者：繁依Fanyi0 | 2024-03-14 10:14:38

赞

踩

选择排序，冒泡排序，插入排序，快速排序及其优化

目录

1 选择排序

1.1 原理

1.2 具体步骤 

1.3 代码实现

1.4 优化

2 冒泡排序

2.1 原理

2.2 具体步骤

2.3 代码实现

2.4 优化

3 插入排序

3.1 原理

3.2 具体步骤 

3.3 代码实现

3.4 优化

4. 快速排序 

4.1 原理

4.2 具体步骤

4.3 代码实现 

4.4 优化 

为了讲解方便，以下排完序后，统一为升序

1 选择排序

1.1 原理

核心思想是通过不断地选择未排序序列中的最小元素，然后将其放到已排序序列的末尾（或未排序列的起始位置）。

 

1.2 具体步骤 

1. 初始状态：所有元素初始都为未排序状态

2 在未排序元素中，找到最小的那个元素的下标

3 与未排序的第一个元素（已排序的末尾元素）交换位置

4 循环 2 ~ 3，直到所有元素都变为已排了的元素

1.3 代码实现

代码实现的关键点：找下标，换位置，以及循环条件。同时也是容易出错的点。

  1. #include<stdio.h>
  2.  
  3. void sort(int* p, int n)
  4. {
  5. 	for (int i = 0; i < n - 1; i++) // < n 也可以，只是无意义的重复，效率更低
  6. 	{
  7. 		int min = i;   // 找出的最小值，最后要放的位置的下标
  8. 		int j = i;
  9. 		for (j = i + 1; j < n; j++)  // 可以=i，只是=i，无意义。
  10. 		{
  11. 			if (p[min] > p[j])
  12. 				min = j;	
  13. 			//  for循环结束后，j会++  
  14. 			if (n - 1 == j)
  15. 				break;
  16. 		}
  17. 		// 交换数据
  18. 		int temp = p[i];
  19. 		p[i] = p[min];
  20. 		p[min] = temp;
  21. 	}
  22. }
  23.  
  24. int main()
  25. {
  26. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  27. 	int sz = sizeof(arr) / sizeof(arr[0]);
  28.  
  29. 	sort(arr, sz);  // 选择排序
  30.  
  31. 	for (int i = 0; i < sz; i++)
  32. 	{
  33. 		printf("%d ", arr[i]);
  34. 	}
  35.  
  36. 	return 0;
  37. }

1.4 优化

 原来一趟只找出最小值，现在一趟既找出最小值，也找出最大值，循环的次数就减半了。

  1. #include<stdio.h>
  2.  
  3. void swap(int* a, int* b)
  4. {
  5. 	int temp = *a;
  6. 	*a = *b;
  7. 	*b = temp;
  8. }
  9.  
  10. void sort(int* p, int n)
  11. {
  12. 	// 循环趟数减半，可以了就要停止，不然就会继续换，反而无序
  13. 	for (int i = 0; i <= n / 2 + 1; i++) 
  14. 	{
  15. 		int min = i;   // 找出的最小值的下标
  16. 		int max = n -i - 1; // 找出的最大值的下标
  17. 		int j = i;
  18. 		for (j = i; j < n - i; j++) 
  19. 		{
  20. 			if (p[min] > p[j])
  21. 				min = j;
  22. 			if (p[max] < p[j])
  23. 				max = j;
  24. 			if (n - 1 - i == j)
  25. 				break;
  26. 		}
  27. 	
  28. 		// 交换数据
  29. 	   // 当最小值与最大值恰好位置相反，换两次=没换
  30. 		if (!(p[min] == p[n - 1 - i] || p[i] == p[max]))
  31. 		{
  32. 			swap(&p[i], &p[min]);
  33. 			swap(&p[n - 1 - i], &p[max]);
  34. 		}
  35. 		else
  36. 		{
  37. 			swap(&p[i], &p[n - 1 - i]);
  38. 		}
  39. 	}
  40. }
  41.  
  42. int main()
  43. {
  44. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  45. 	int sz = sizeof(arr) / sizeof(arr[0]);
  46.  
  47. 	sort(arr, sz);  // 选择排序优化
  48.  
  49. 	for (int i = 0; i < sz; i++)
  50. 	{
  51. 		printf("%d ", arr[i]);
  52. 	}
  53.  
  54. 	return 0;
  55. }

2 冒泡排序

2.1 原理

核心思想是通过重复交换相邻元素来实现排序。

类比选择排序，相当于从右往左开始排，每次在未排序中找出最大值，放在已排序的前一个位置。

 

2.2 具体步骤

1. 从左往右相邻元素比较，让大的数不断右移

2. 循环1，直至每个已排序的元素 = 所有元素的个数

2.3 代码实现

关键点：循环条件的控制，以及交换（大的靠右）

  1. #include<stdio.h>
  2.  
  3. void sort(int arr[], size_t sz)
  4. {
  5. 	for (int i = 0; i < sz - 1; i++)
  6. 	{
  7. 		// 在这里j可以 < sz - 1;
  8. 		// 在本段代码中交换位置是有条件的
  9. 		// < sz - 1;进去了也不会执行
  10. 		// 选择排序从哪开始到哪结束就必须是那样
  11. 		// 不可能在再在排了序中挑最大最小值
  12. 		for (int j = 0; j < sz - 1 - i; j++)
  13. 		{
  14. 			if (arr[j] > arr[j + 1])
  15. 			{
  16. 				int temp = arr[j];
  17. 				arr[j] = arr[j + 1];
  18. 				arr[j + 1] = temp;
  19. 			}
  20. 		}
  21. 	}
  22. }
  23.  
  24. int main()
  25. {
  26. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  27. 	size_t sz = sizeof(arr) / sizeof(arr[0]);
  28. 	
  29. 	sort(arr, sz);  // 冒泡排序
  30. 	
  31. 	for (int i = 0; i < sz; i++)
  32. 	{
  33. 		printf("%d ", arr[i]);
  34. 	}
  35. 	
  36. 	return 0;
  37. }

2.4 优化

如果我们一开始拿到的数组就是有序的话，我们还是不得不执行那循环套循环，效率就很低。我们可以先假设已达到了有序状态，如果交换了，就通过修改flag的值来办，这样就可以提前跳出循环了。

  1. #include<stdio.h>
  2.  
  3. void sort(int arr[], size_t sz)
  4. {
  5. 	for (int i = 0; i < sz - 1; i++)
  6. 	{
  7. 		// 假设已经到达了有序状态
  8. 		int flag = 1;
  9. 		for (int j = 0; j < sz - 1 - i; j++)
  10. 		{
  11. 			if (arr[j] > arr[j + 1])
  12. 			{
  13. 				int temp = arr[j];
  14. 				arr[j] = arr[j + 1];
  15. 				arr[j + 1] = temp;
  16. 				// 交换了，说明无序
  17. 				flag = 0;
  18. 			}
  19. 		}
  20. 		if (flag)
  21. 		{
  22. 			break;
  23. 		}
  24. 	}
  25. }
  26.  
  27. int main()
  28. {
  29. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  30. 	size_t sz = sizeof(arr) / sizeof(arr[0]);
  31.  
  32. 	sort(arr, sz);  // 冒泡排序优化
  33.  
  34. 	for (int i = 0; i < sz; i++)
  35. 	{
  36. 		printf("%d ", arr[i]);
  37. 	}
  38.  
  39. 	return 0;
  40. }

3 插入排序

3.1 原理

核心思想是构建有序序列。将未排序的元素逐个插入到已排序的部分。

左边是已排序的，右边是未排序的。未排序的从左到右第一个，放到已排序列中开始交换，大的就右移，移到不能再移。

 

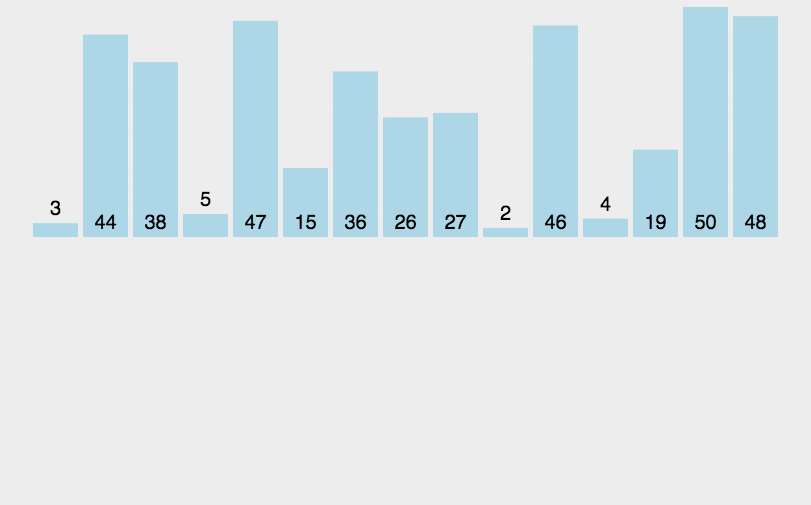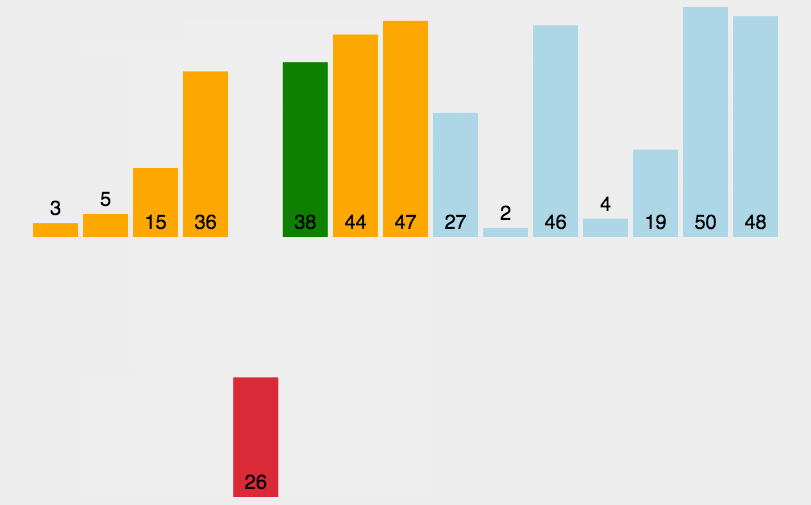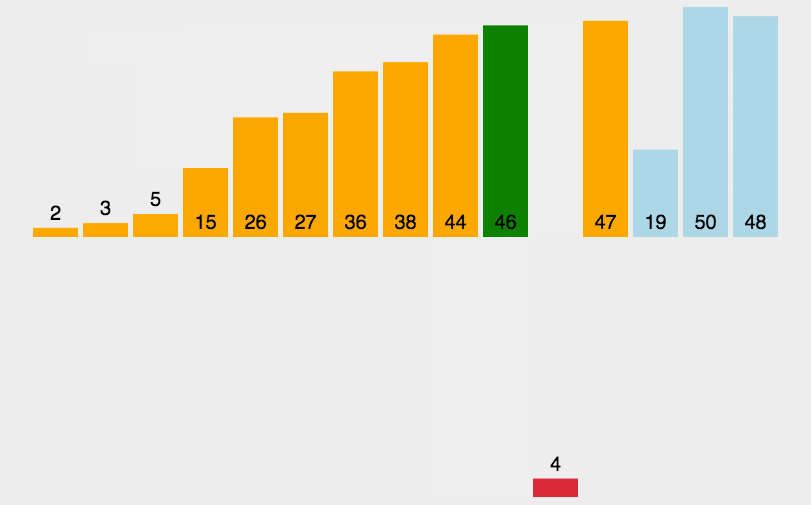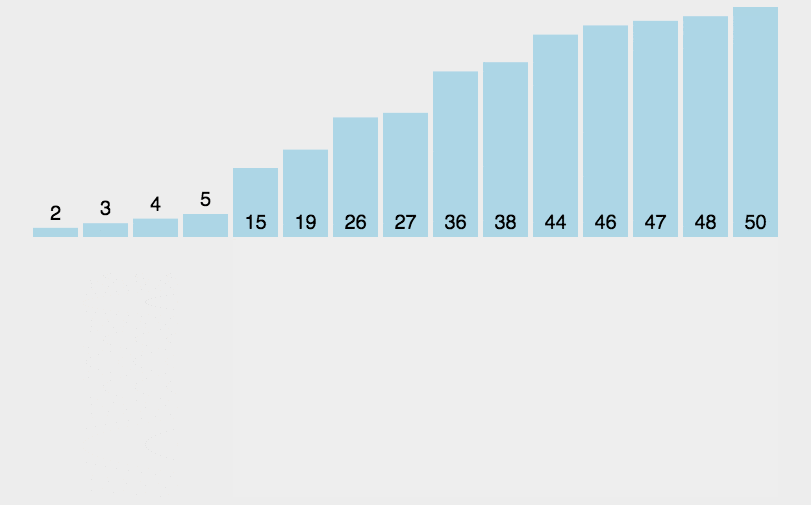
3.2 具体步骤 

1. 初始化：左边第一个是已排序的，右边都是未排序的。

2 交换位置：未排序的第一个进入排序中，比较大小，大的右移，移到不能再移

3 循环 1 ~ 2，直到遍历数组中的所有元素

3.3 代码实现

关键点： 交换位置的意识，递推的意识

  1. #include<stdio.h>
  2.  
  3. void sort(int arr[], size_t sz)
  4. {
  5. 	// 外层每一次循环都会让已排序的元素+1
  6. 	for (int i = 1; i < sz; i++)
  7. 	{
  8. 		int j = i;
  9. 		while (j >= 1 && arr[j] < arr[j - 1])
  10. 		{
  11. 			// 交换位置
  12. 			arr[j - 1] = arr[j] ^ arr[j - 1];
  13. 			arr[j] = arr[j] ^ arr[j - 1];
  14. 			arr[j - 1] = arr[j] ^ arr[j - 1];
  15. 			j--;
  16. 		}
  17.  
  18. 	}
  19. }
  20.  
  21. int main()
  22. {
  23. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  24. 	size_t sz = sizeof(arr) / sizeof(arr[0]);
  25.  
  26. 	sort(arr, sz);  // 插入排序
  27.  
  28. 	for (int i = 0; i < sz; i++)
  29. 	{
  30. 		printf("%d ", arr[i]);
  31. 	}
  32.  
  33. 	return 0;
  34. }

3.4 优化

所谓优化算法就更接近于通俗意义上的插入，找到该插入的的地方，再进行插入。即对插入的位置实行二分查找。

  1. #include<stdio.h>
  2.  
  3. // 返回值是该数插入进去后的下标
  4. int find(int arr[], int sz)
  5. {
  6. 	//    1 2 4 5 7 8 9   6
  7. 	int left = 0;
  8. 	int right = sz - 1;
  9. 	while (left < right)
  10. 	{
  11. 		// 防止陷入死循环
  12. 		if (left == right)
  13. 			break;
  14. 		int mid = right + (left - right) / 2;
  15. 		if (arr[mid] > arr[sz])
  16. 		{
  17. 			right = mid - 1;
  18. 		}
  19. 		else if (arr[mid] < arr[sz])
  20. 		{
  21. 			left = mid + 1;
  22. 		}
  23. 		else
  24. 		{
  25. 			right = left;
  26. 			break;
  27. 		}
  28. 	}
  29. 	if (arr[sz] < arr[right])
  30. 	{
  31. 		return right;
  32. 	}
  33. 	else
  34. 	{
  35. 		return right + 1;
  36. 	}
  37. }
  38.  
  39. void sort(int arr[], size_t sz)
  40. {
  41. 	for (int i = 1; i < sz; i++)
  42. 	{
  43. 		// 本质：二分查找 + 交换
  44. 		int temp = arr[i]; // 将要排序的数暂时储存起来
  45. 		
  46. 		// 二分查找找到应该插入的下标
  47. 		int final_local = find(arr, i);
  48. 		// 该右移的右移
  49. 		for (int j = i - 1; j >= final_local; j--)
  50. 		{
  51. 			arr[j + 1] = arr[j];
  52. 		}
  53. 		arr[final_local] = temp;
  54. 	}
  55. }
  56.  
  57. int main()
  58. {
  59. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  60. 	size_t sz = sizeof(arr) / sizeof(arr[0]);
  61.  
  62. 	sort(arr, sz);  // 插入排序优化
  63.  
  64. 	for (int i = 0; i < sz; i++)
  65. 	{
  66. 		printf("%d ", arr[i]);
  67. 	}
  68.  
  69. 	return 0;
  70. }

4. 快速排序 

4.1 原理

核心思想是分治法。一分为二，左边比某个基准数小，右边比某个基准数大，左边右边又一分为二，直至不可再分

 

4.2 具体步骤

  1. 从数列中随便挑一个数作为基准数（我选的是最后一个数）;

  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。

  3. 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序；

4.3 代码实现 

关键点：递归的思想，函数要被调用，要写得一般一些

  1. #include<stdio.h>
  2. /*
  3. 函数功能：将最后一个元素作为基准数
  4.          小于它的放左边，大于它的放右边
  5. 返回值：基准数最后的位置
  6. */
  7. int partition(int arr[], int start, int end)
  8. {
  9. 	// 遍历基准元素前的所有元素
  10. 	for (int i = end - 1; i >= start; i--)
  11. 	{
  12. 		if (arr[i] > arr[end])
  13. 		{
  14. 			int temp = arr[i];
  15. 			arr[i] = arr[end - 1];
  16. 			arr[end - 1] = arr[end];
  17. 			arr[end] = temp;
  18. 			end -= 1;
  19. 		}
  20. 	}
  21. 	return end;
  22. 	//  2 1 3 2
  23. }
  24.  
  25. void QuickSort(int arr[], int start, int end)
  26. {
  27. 	if (start < end)
  28. 	{
  29. 		// 函数最后返回的是排过后基准元素的位置
  30. 		int pivot = partition(arr, start, end);
  31. 		// 递推式的一分为二
  32. 		QuickSort(arr, start, pivot - 1);
  33. 		QuickSort(arr, pivot + 1, end);
  34. 	}
  35. }
  36.  
  37. int main()
  38. {
  39. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  40. 	size_t sz = sizeof(arr) / sizeof(arr[0]);
  41.  
  42. 	// 以后还要调用，需写得一般一些
  43. 	QuickSort(arr, 0, sz - 1);  // 快速排序
  44.  
  45. 	for (int i = 0; i < sz; i++)
  46. 	{
  47. 		printf("%d ", arr[i]);
  48. 	}
  49.  
  50. 	return 0;
  51. }
  52.

4.4 优化 

快速排序的效率在于其平均时间复杂度为O(nlogn)，这使其成为实际应用中非常受欢迎的一种排序算法。然而，在最坏的情况下，其时间复杂度会退化到O(n^2)，这通常发生在每次选择的基准都是最大或最小元素时。为了避免这种情况，可以采用随机选择基准或者三数取中等策略来优化快速排序的性能。下面演示随机选择的优化

  1. #include<stdio.h>
  2. #include<stdlib.h>
  3. #include<time.h>
  4. /*
  5. 函数功能：将最后一个元素作为基准数
  6.          小于它的放左边，大于它的放右边
  7. 返回值：基准数最后的位置
  8. */
  9. int partition(int arr[], int start, int end)
  10. {
  11. 	int end_temp = end;
  12. 	end = rand() % (end - start) + start + 1;
  13. 	// 把左边大的甩到右边
  14. 	for (int i = end - 1; i >= start; i--)
  15. 	{
  16. 		if (arr[i] > arr[end])
  17. 		{
  18. 			int temp = arr[i];
  19. 			arr[i] = arr[end - 1];
  20. 			arr[end - 1] = arr[end];
  21. 			arr[end] = temp;
  22. 			end -= 1;
  23. 		}
  24. 	}
  25. 	// 把右边小的甩到左边
  26. 	for (int i = end + 1; i <= end_temp; i++)
  27. 	{
  28. 		if (arr[i] < arr[end])
  29. 		{
  30. 			int temp = arr[i];
  31. 			arr[i] = arr[end + 1];
  32. 			arr[end + 1] = arr[end];
  33. 			arr[end] = temp;
  34. 			end += 1;
  35. 		}
  36. 	}
  37. 	return end;
  38. 	//  2 1 3 2
  39. }
  40.  
  41. void QuickSort(int arr[], int start, int end)
  42. {
  43. 	if (start < end)
  44. 	{
  45. 		// 函数最后返回的是排过后基准元素的位置
  46. 		int pivot = partition(arr, start, end);
  47. 		// 递推式的一分为二
  48. 		QuickSort(arr, start, pivot - 1);
  49. 		QuickSort(arr, pivot + 1, end);
  50. 	}
  51. }
  52.  
  53. int main()
  54. {
  55. 	srand((unsigned int)time(NULL));
  56. 	int arr[] = { 9,6,8,-1,0,5,2,8 };
  57. 	size_t sz = sizeof(arr) / sizeof(arr[0]);
  58.  
  59. 	// 以后还要调用，需写得一般一些
  60. 	QuickSort(arr, 0, sz - 1);  // 快速排序
  61.  
  62. 	for (int i = 0; i < sz; i++)
  63. 	{
  64. 		printf("%d ", arr[i]);
  65. 	}
  66.  
  67. 	return 0;
  68. }
  69.

感谢观看！！！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/233266
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号