- 1NSLocalizedString用法
- 2【华为OD机试真题 JS语言】464、 宽度最小的子矩阵、最小矩阵宽度 | 机试真题+思路参考+代码解析（最新C卷抽中）（本题100%）
- 3快速、内存高效的注意力 FlashAttention BERT单节点训练最快_flashattention 原理
- 4【树莓派-网络监控（3）角度遥控】基于python3控制两自由度舵机，实现摄像头拍摄角度的遥控_树莓派使用舵机控制摄像头
- 5多家头部企业宣布「启动鸿蒙原生应用开发」，你看好鸿蒙系统走向「独立」吗？
- 6文本识别CRNN模型介绍以及pytorch代码实现
- 7第17章 配置客户端认证_max_prepared_transactions greater than
- 8[SpringBoot系列]数据层技术解析_springboot大数据有什么用
- 9Midjourney实战案例 3 |商业变现用AI做表情包制作/赚钱教程_madjourney怎么变现
- 10ClickHouse 集群快速搭建_docker部署clickhouse集群
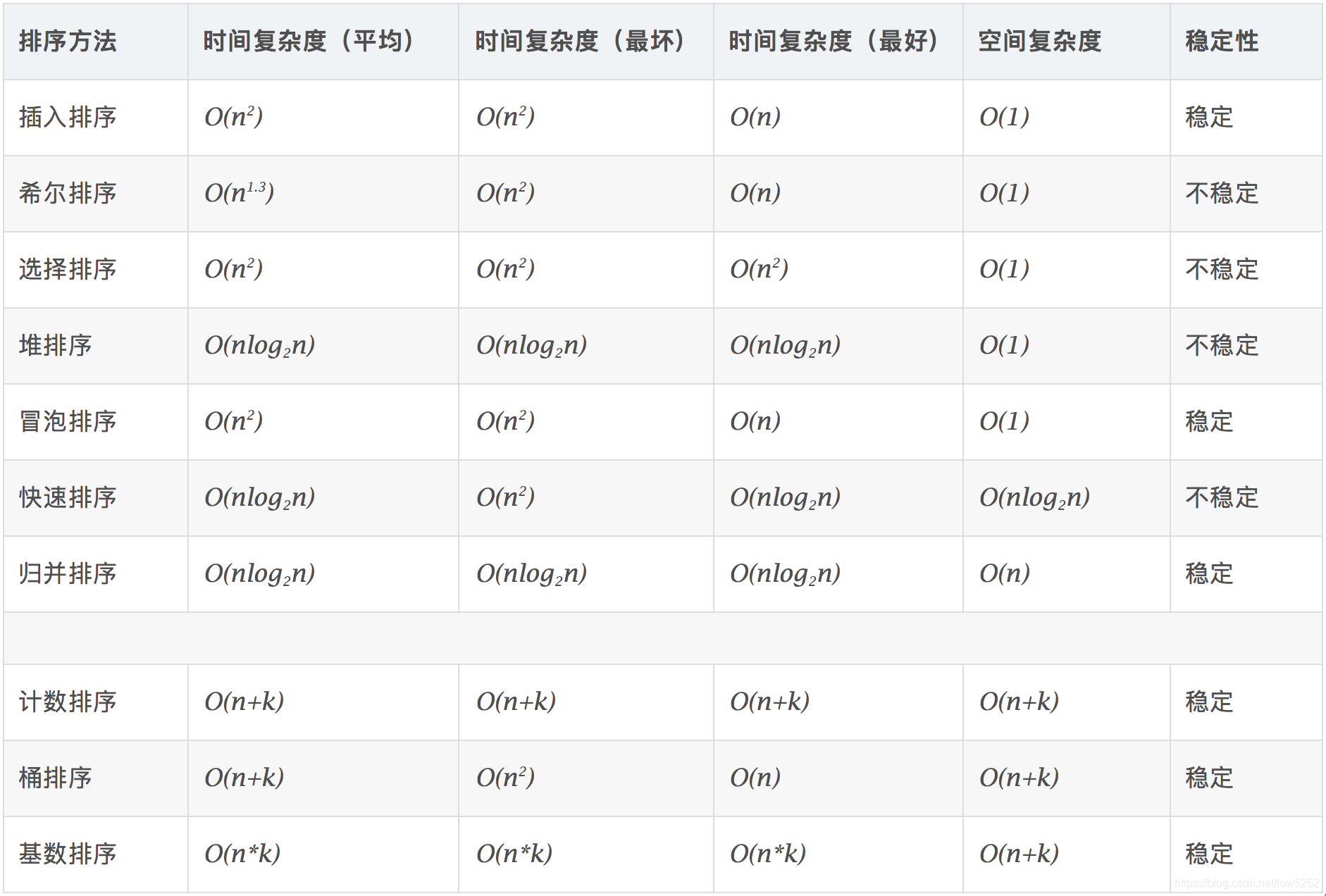
常见的几种排序算法（c++）_c++排序算法
赞
踩
一、冒泡排序
1、算法思想
冒泡排序是一种简单的排序算法，通过循环遍历，将临近的两个元素进行比较，满足排序规则时，进行下一组元素对比，当不满足排序规则时，将两个元素交换位置，再继续进行下一组元素对比，确保最大的元素在一遍循环过后一定排在最后面，然后最后通过最多n2次循环对比，直到完全有序。
2、算法描述
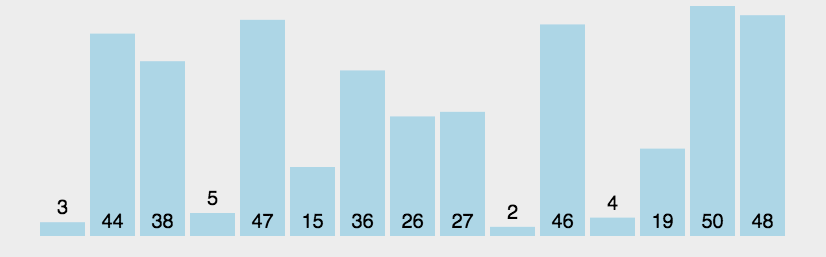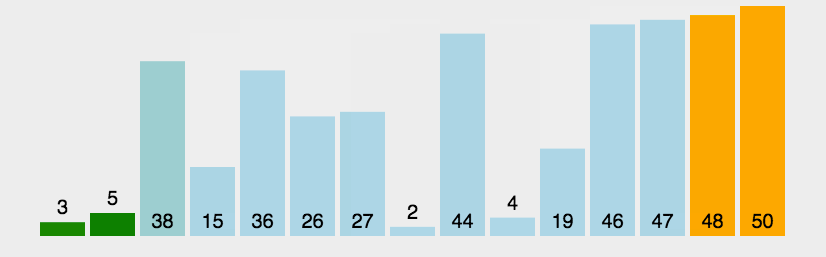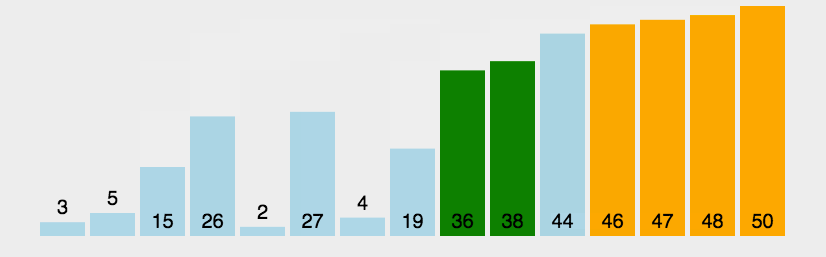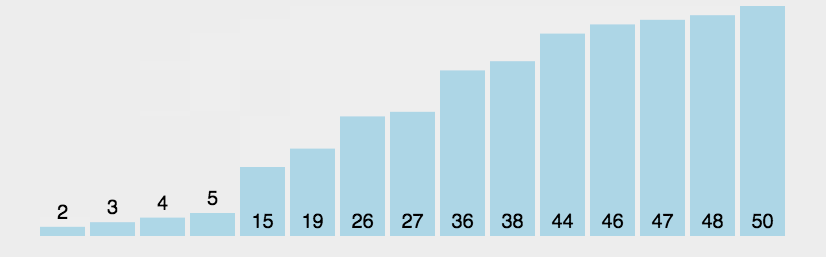
（1）比较两个相邻的元素，如果第一个比第二个大，那么就交换他们的位置。
（2）重复步骤（1）的操作，依次比较两两相邻的两个元素。所有元素对比过后表示一次循环结束。
（3）至多循环n-1次，重复上面两个步骤。
（4）直到没有任何一组元素需要交换位置表示排序完成。
3、代码实现
void BubbleSort(int* slist,int length) { int temp; for (int i = 0; i < length - 1; i++) { for (int j = 0; j < length - 1 - i; j++) { if (slist[j] > slist[j + 1]) { temp = slist[j]; slist[j] = slist[j + 1]; slist[j + 1] = temp; } } } } int main() { int sortlist[] = { 5,0,4,1,8,3,7 }; BubbleSort(sortlist,7); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
4、算法复杂度
最好的情况为正序，只需要一遍遍历，所以时间复杂度为O(n),最坏的情况为逆序，需要遍历n2次，所以时间复杂度为O(n2)。由于只有一个交换的变量temp需要内存，所以空间复杂度为O(1)。
二、插入排序
1、算法思想
将列表中的每个元素依次和之前排好序的元素进行比较，找到合适的位置插入，使之前有序的列表保持依然有序。
2、算法描述
（1）从第2个元素开始，选取第2个元素（i），认为第1个元素为一个只有一个元素的有序列表。
（2）将选取的元素与之前的元素依次比较，如果选取的元素小于于列表中的元素，交换他们的位置。
（3）选取下一个元素（i+1），重复步骤（2），直至列表中的每个元素都进行了步骤（2）的操作。
3、代码实现
//方法一 void InsertSort1(int* slist,int length) { int temp; for (int i = 1; i < length; i++) { int j = i -1; while (slist[j] > slist[j+1] && j >= 0) { //交换位置 temp = slist[j]; slist[j] = slist[j+1]; slist[j+1] = temp; j--; /*或者这样交换*/ // slist[j+1] = slist[j] + slist[j+1]; // slist[j] = slist[j+1] - slist[j]; // slist[j+1] = slist[j+1] - slist[j]; // j--; } } } //方法二 void InsertSort2(int* slist,int length) { for (int i = 1; i < length; i++) { int j = i - 1; int number = slist[i]; while (j >= 0 && slist[j] > number) { slist[j+1] = slist[j]; j--; } slist[j+1] = number; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
4、算法复杂度
最好的情况为正序，只需要一遍遍历，所以时间复杂度为O(n),最坏的情况为逆序，需要遍历n2次，所以时间复杂度为O(n2)。空间复杂度为O(1)。
三、选择排序
1、算法思想
从头开始，遍历列表找到最小值，把最小的值放在第一个位置，在遍历找到第二小的值放在第一个后面，以此类推，知道最后一个排好序。
2、算法描述
（1）遍历整个列表N个元素，找到最小的元素，与第一个元素交换位置。
（2）遍历剩余的N-1个元素，找到最小的元素，将它排在剩余N-1个元素的第一个。
（3）以此类推，重复步骤（2），直到N-1小于1。
3、代码实现
void SelectSort(int* slist, int length) { int min; int temp; for (int i = 0; i < length; i++) { min = i; for (int j = i + 1; j < length; j++) { if (slist[j] < slist[min]) { min = j; } } temp = slist[i]; slist[i] = slist[min]; slist[min] = temp; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
4、算法复杂度
不管最后还是最坏的情况，选择排序的时间复杂度都是O(n2)，空间复杂度为O(1)。
四、归并排序
1、算法思想
归并排序采用分治的思想，将一个列表分为多个子列表，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
2、算法描述
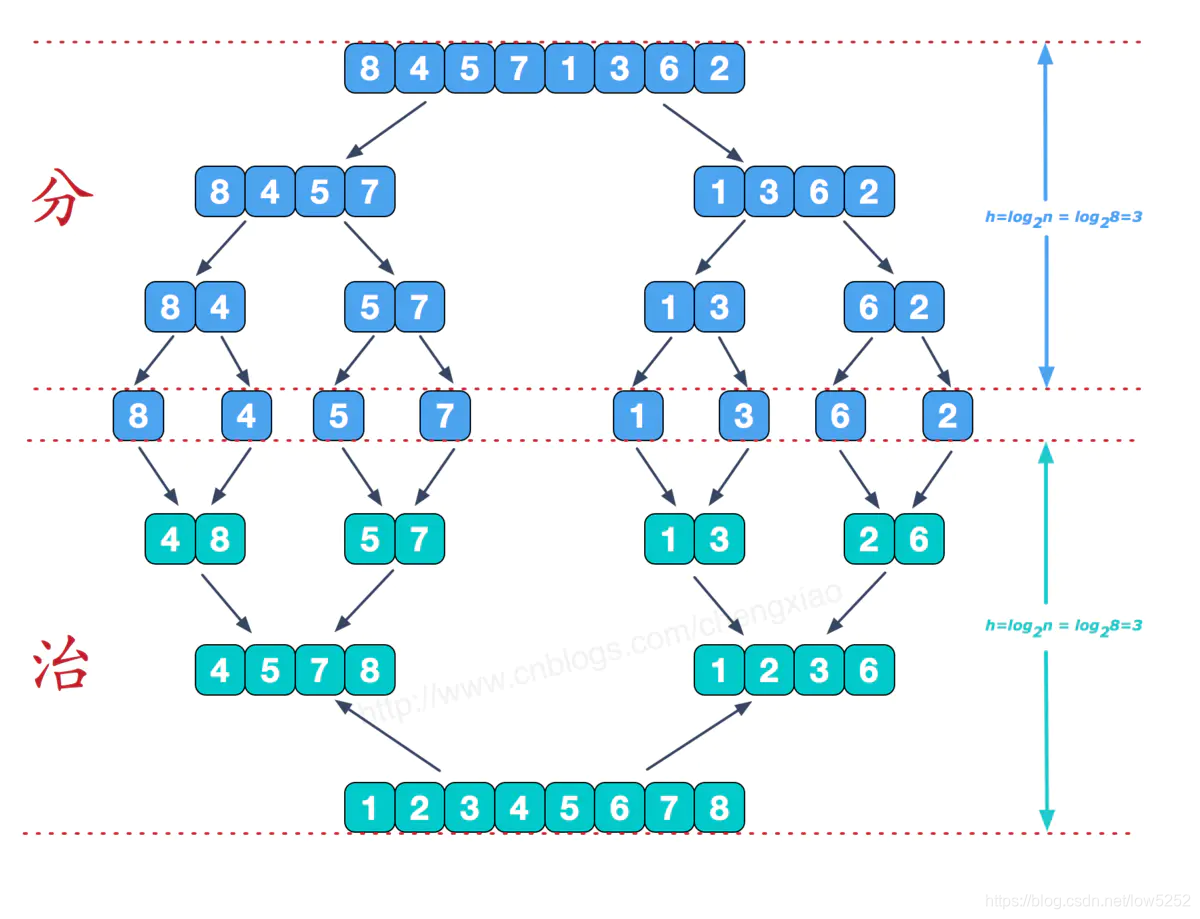
（1）将列表元素对半分开，分为两个列表。
（2）重复步骤（1），直至每个列表只有一个元素。
（3）将两个相邻的列表排序，直至真个列表有序。
3、代码实现
//排序 void MergeSort(int sourceArr[], int tempArr[], int startIndex, int midIndex, int endIndex) { //i:第一个待排序的起始位置， int i = startIndex; //j:第二个待排序的起始位置， int j = midIndex + 1; int k = startIndex; while (i != midIndex + 1 && j != endIndex+1) { if (sourceArr[i] > sourceArr[j]) { tempArr[k] = sourceArr[j]; k++; j++; } else { tempArr[k] = sourceArr[i]; k++; i++; } } //将两个中未排序的添加到tempArr中 while (i != midIndex + 1) { tempArr[k] = sourceArr[i]; i++; k++; } //将两个中未排序的添加到tempArr中 while (j != endIndex+1) { tempArr[k] = sourceArr[j]; j++; k++; } //将tempArr中的元素赋值给sourceArr for (int i = startIndex; i <= endIndex; i++) { sourceArr[i] = tempArr[i]; } } //分解递归 void BranchSort(int sourceArr[], int tempArr[], int startIndex, int endIndex) { if (startIndex < endIndex) { int mid = startIndex + (endIndex - startIndex) / 2; BranchSort(sourceArr, tempArr, startIndex, mid); BranchSort(sourceArr, tempArr, mid+1, endIndex); MergeSort(sourceArr, tempArr, startIndex, mid, endIndex); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
4、算法复杂度
归并排序是稳定排序算法，假设数组长度为n，那么拆分数组共需logn, 又每步都是一个普通的合并子数组的过程，时间复杂度为O(n)， 故其综合时间复杂度为O(nlogn)。另一方面， 归并排序多次递归过程中拆分的子数组需要保存在内存空间， 其空间复杂度为O(n)。
五、希尔排序
1、算法思想
希尔排序，也称递减增量排序算法。将整个列表根据增量分为若干个子列表分别进行插入排序。随着增量的减小，列表趋于基本有序，当增量为1时，相当再做一次插入排序，使列表有序。
2、算法描述
（1）选择一个增量gap，一般为列表长度的一半。
（2）将列表中元素下标每隔gap的元素组成一个新的子列表。
（3）对每个子列表进行插入排序。
（4）将gap去原来的一半，重复步骤（2）（3），直到gap小于1。
3、代码实现
void ShellSort(int* slist, int length) { int temp; //gap为增量，一般取长度的一般 int gap = length / 2; //当增量小于1时结束排序 while (gap >= 1) { //最多分为gap个列表 for (int i = 0; i < gap; i++) { //下面的代码为一个简单的插入排序，只是插入排序的数组下标每次移动的不是1而是gap for (int j = i+gap; j < length; j = j + gap) { if (slist[j] < slist[j-gap]) { int k = j - gap; int temp = slist[j]; while (k >= 0 && slist[k] > temp) { slist[k + gap] = slist[k]; k = k - gap; } slist[k+gap] = temp; } } } //增量递减 gap = gap/ 2; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
4、算法复杂度
希尔排序是不稳定的排序，它时间复杂度和步长的选择有关。
看如下两个增量序列：
n/2、n/4、n/8...1
1 、3 、7 ...2^k-1
- 1
- 2
第一个序列称为希尔增量序列，使用希尔增量时，希尔排序在最坏情况下的时间复杂度为O(n2)。
第二个序列称为Hibbard增量序列，使用Hibbard增量时，希尔排序在最坏情况下的时间复杂度为O(n3/2)。
六、快速排序
1、算法思想
快速排序采用分治的思想，通通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以 递归 进行，以此达到整个数据变成有序序列。
2、算法描述
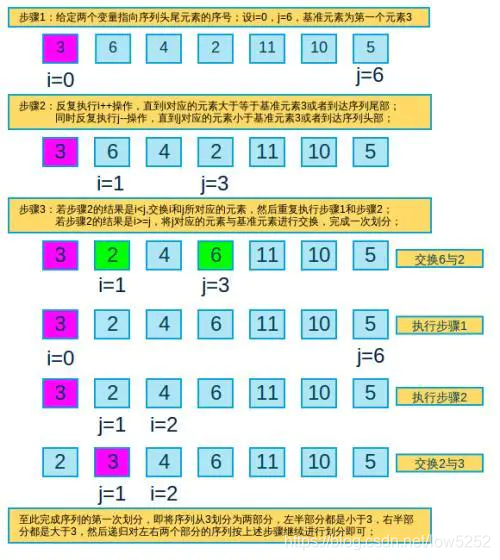
（1）选定一个基准元素
（2）从右往左找到比基准元素小的元素
（3）从左往右找到比基准元素大的元素
（4）交换左右找到的两个元素的位置
（5）重复上面（2）（3）（4）步，直至左右两个元素相遇。
3、代码实现
void QuickSort(int* slist, int left, int right) { if (left >= right) { return; } int i = left; int j = right; int key = slist[left]; int temp; //直到遍历完整个列表 while (i < j) { //从右到左找到小于key的下标 while (i<j&&slist[j] >= key) { j--; } //从左到右找到大于key的下标 while (i<j && slist[i] <= key) { i++; } //交换找到的两个元素,保证小的元素在前，大的元素在后 if (i < j) { temp = slist[i]; slist[i] = slist[j]; slist[j] = temp; } } //将key元素交换到中间，确保分为大小两个列表 temp = slist[left]; slist[left] = slist[j]; slist[j] = temp; QuickSort(slist, left, j - 1); QuickSort(slist, j + 1, right); } void QuickSort2(int* slist, int left, int right) { if (left >= right) { return; } int j = left-1; int key = slist[right]; int temp; for (int i = left; i < right; i++) { //遍历整个列表，找到小于key的元素个数，并且通过交换位置，让他们的下标都在j的前面 if (slist[i] < key) { j++; if (i != j) { temp = slist[i]; slist[i] = slist[j]; slist[j] = temp; } } } //将key的位置与j+1的位置互换，保证将slist列表分为小于slist[j+1]与大于slist[j+1]的两个列表 slist[right] = slist[j + 1]; slist[j + 1] = key; QuickSort2(slist,left,j); QuickSort2(slist, j+2, right); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
4、算法复杂度
快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N2)，它的平均时间复杂度为O(NlogN)。
七、堆排序
堆排序实际上是利用堆的性质来进行排序的，要知道堆排序的原理我们首先一定要知道什么是堆。
堆的定义：
堆实际上是一棵完全二叉树。
堆满足两个性质:
1、堆的每一个父节点都大于（或小于）其子节点；
2、堆的每个左子树和右子树也是一个堆。
堆的分类：
堆分为两类：
1、最大堆（大顶堆）：堆的每个父节点都大于其孩子节点；
2、最小堆（小顶堆）：堆的每个父节点都小于其孩子节点；
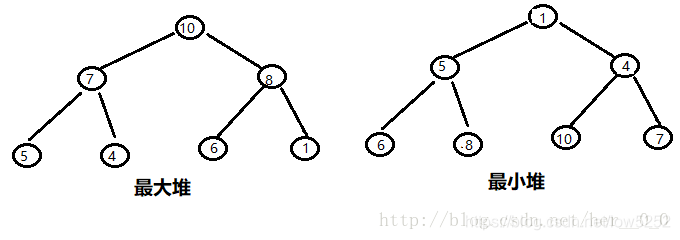
堆的存储：
一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如下图所示：
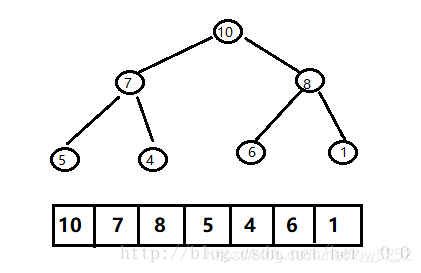
堆排序：
由上面的介绍我们可以看出堆的第一个元素要么是最大值（大顶堆），要么是最小值（小顶堆），这样在排序的时候（假设共n个节点），直接将第一个元素和最后一个元素进行交换，然后从第一个元素开始进行向下调整至第n-1个元素。所以，如果需要升序，就建一个大堆，需要降序，就建一个小堆。
堆排序的步骤分为三步:
1、建堆（升序建大堆，降序建小堆）；
2、交换数据；
3、向下调整。
假设我们现在要对数组arr[]={8,5,0,3,7,1,2}进行排序（降序）：
首先要先建小堆：
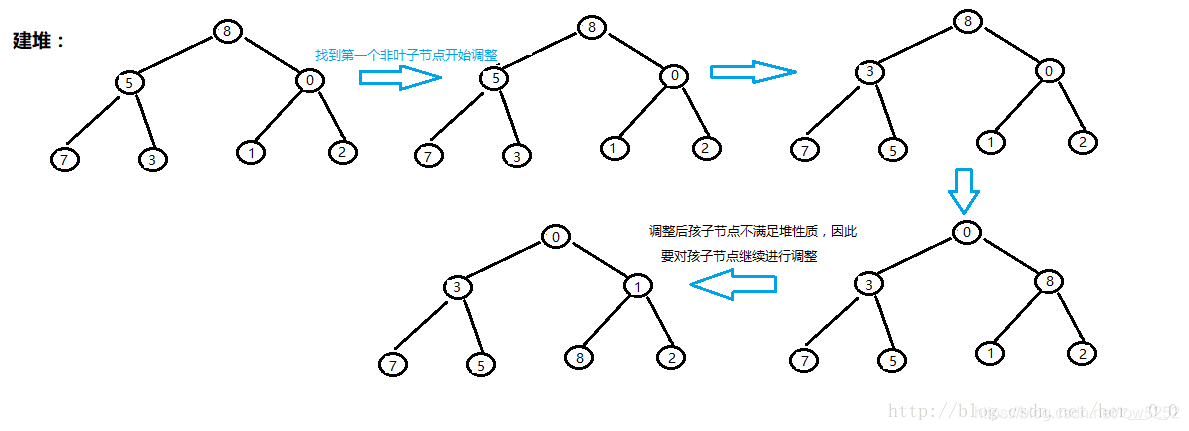
堆建好了下来就要开始排序了：
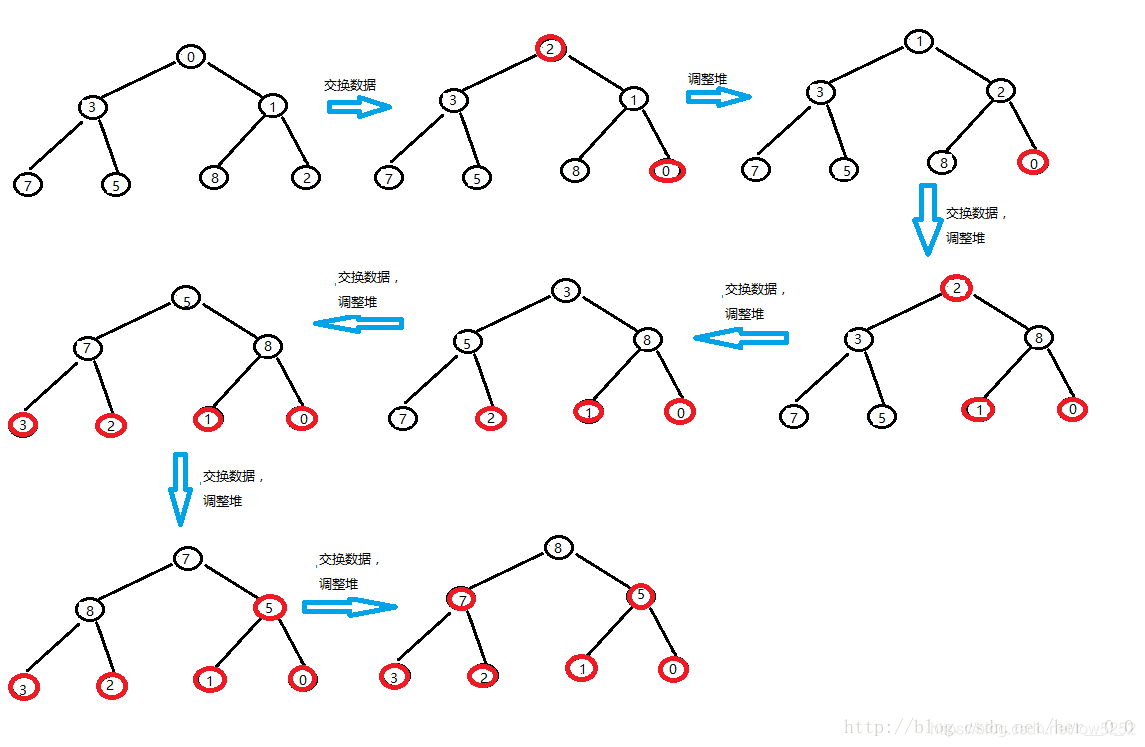
现在这个数组就已经是有序的了。
算法实现：
1 //堆排序 2 /* 3 大顶堆sort之后，数组为从小到大排序 4 */ 5 //====调整===== 6 void AdjustHeap(int* h, int node, int len) //----node为需要调整的结点编号，从0开始编号;len为堆长度 7 { 8 int index=node; 9 int child=2*index+1; //左孩子，第一个节点编号为0 10 while(child<len) 11 { 12 //右子树 13 if(child+1<len && h[child]<h[child+1]) 14 { 15 child++; 16 } 17 if(h[index]>=h[child]) break; 18 Swap(h[index],h[child]); 19 index=child; 20 child=2*index+1; 21 } 22 } 23 24 25 //====建堆===== 26 void MakeHeap(int* h, int len) 27 { 28 for(int i=len/2;i>=0;--i) 29 { 30 AdjustHeap(h, i, len); 31 } 32 } 33 34 //====排序===== 35 void HeapSort(int* h, int len) 36 { 37 MakeHeap(h, len); 38 for(int i=len-1;i>=0;--i) 39 { 40 Swap(h[i],h[0]); 41 AdjustHeap(h, 0, i); 42 } 43 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
八、基数排序
基数排序与本系列前面讲解的七种排序方法都不同，它不需要比较关键字的大小。
它是根据关键字中各位的值，通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。
1.LSD(低位到高位的排序)
不妨通过一个具体的实例来展示一下，基数排序是如何进行的。
设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。
我们知道，任何一个阿拉伯数，它的各个位数上的基数都是以0~9来表示的。
所以我们不妨把0~9视为10个桶。
我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。例如：R[0] = 50，个位数上是0，将这个数存入编号为0的桶中。
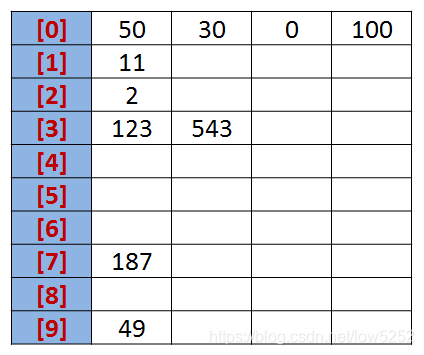
分类后，我们在从各个桶中，将这些数按照从编号0到编号9的顺序依次将所有数取出来。
这时，得到的序列就是个位数上呈递增趋势的序列。
按照个位数排序：
{50, 30, 0, 100, 11, 2, 123, 543, 187, 49}
- 1
接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。
LSD 算法实现：
1 int GetMaxDight(int* h, int len) 2 { 3 if(h==NULL) return 0; 4 if(len<1) return 0; 5 6 int max=h[0]; 7 for(int i=1;i<len;++i) 8 { 9 if(h[i]>max) max=h[i]; 10 } 11 12 int digit=1; 13 while(max/10!=0) 14 { 15 max/=10; 16 ++digit; 17 } 18 19 return digit; 20 } 21 22 int GetReminder(int value,int digit) 23 { 24 int div=1; 25 for(int i=1;i<digit;++i) 26 div*=10; 27 28 return value/div%10; 29 } 30 31 void RadixSort_LSD(int* h, int len) 32 { 33 if(h==NULL) return; 34 if(len<=1) return; 35 36 int digit=GetMaxDight(h,len); 37 //printf("MaxDigit:%d\n", digit); 38 39 int count[10]={0}; 40 int *tmp=(int*)calloc(len,sizeof(int)); 41 42 for(int d=1;d<=digit;++d) 43 { 44 memset(count,0,sizeof(count)); 45 46 for(int i=0;i<len;++i) 47 { 48 count[GetReminder(h[i],d)]++; 49 } 50 51 //求右边界 52 for(int i=1;i<10;++i) 53 { 54 count[i]+=count[i-1]; 55 } 56 57 for(int i=len-1;i>=0;--i) 58 { 59 int r=GetReminder(h[i],d); 60 int index=count[r]; 61 tmp[index-1]=h[i]; 62 count[r]--; 63 } 64 65 memcpy(h,tmp,len*sizeof(int)); 66 } 67 68 free(tmp); 69 } 70 71 void RadixSort_LSD_Reverse(int* h, int len) 72 { 73 if(h==NULL) return; 74 if(len<=1) return; 75 76 int digit=GetMaxDight(h,len); 77 //printf("MaxDigit:%d\n", digit); 78 79 int count[10]={0}; 80 81 int *tmp=(int*)calloc(len,sizeof(int)); 82 83 for(int d=1;d<=digit;++d) 84 { 85 memset(count,0,sizeof(count)); 86 87 for(int i=0;i<len;++i) 88 { 89 count[GetReminder(h[i],d)]++; 90 } 91 92 //printf("haha\n"); 93 94 //求右边界 95 for(int i=8;i>=0;--i) 96 { 97 count[i]+=count[i+1]; 98 } 99 100 101 102 for(int i=len-1;i>=0;--i) 103 { 104 int r=GetReminder(h[i],d); 105 int index=count[r]; 106 tmp[index-1]=h[i]; 107 count[r]--; 108 } 109 110 memcpy(h,tmp,len*sizeof(int)); 111 } 112 113 free(tmp); 114 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
2.MSD(高位到低位排序)
下面我们直接来介绍MSD基数排序的步骤。
MSD基数排序是从最高位开始对序列进行分组，到最低位为止。但是其实现过程是和LSD基数排序不同的，排序过程中需要用到递归函数。
待排序序列
170, 45, 75, 90, 2, 24, 802, 66
- 1
我们看到，这里面的最大的数是3位数。所以说我们开始从百位对这些数进行分组
0: 045, 075, 090,002, 024, 066
1: 170
2-7: 空
8: 802
9: 空
- 1
- 2
- 3
- 4
- 5
从这里开始就和LSD基数排序有差别了。在LSD基数排序中，每次分好组以后开始对桶中的数据进行收集。然后根据下一位，对收集后的序列进行分组。而对于MSD，在这里不会对桶中的数据进行收集。我们要做的是检测每个桶中的数据。当桶中的元素个数多于1个的时候，要对这个桶递归进行下一位的分组。
在这个例子中，我们要对0桶中的所有元素根据十位上的数字进行分组
0: 002
1: 空
2: 024
3: 空
4: 045
5: 空
6: 066
7: 075
8: 空
9: 090
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
按照上面所说，我们应该再递归的对每个桶中的元素根据个位上的数进行分组。但是我们发现，现在在每个桶中的元素的个数都是小于等于1的。因此，到这一步我们就开始回退了。也就是说我们开始收集桶中的数据。收集完成以后，回退到上一层。此时按照百位进行分组的桶变成了如下的形式
0: 002, 024, 045,066, 075, 090
1: 170
2-7: 空
8: 802
9: 空
- 1
- 2
- 3
- 4
- 5
然后我们在对这个桶中的数据进行收集。收集起来以后序列如下
2, 24, 45, 66, 75, 90, 170, 802
- 1
整个MSD基数排序就是按照上面的过程进行的。
在我对MSD基数排序步骤进行叙述的时候，中间递归函数的过程可能叙述的不够清楚。我个人建议对递归函数不了解的可以先了解一下递归函数的原理，然后再回来看这个过程可能对MSD基数排序过程更容易理解。
算法实现：
1 int GetMaxDight(int* h, int len) 2 { 3 if(h==NULL) return 0; 4 if(len<1) return 0; 5 6 int max=h[0]; 7 for(int i=1;i<len;++i) 8 { 9 if(h[i]>max) max=h[i]; 10 } 11 12 int digit=1; 13 while(max/10!=0) 14 { 15 max/=10; 16 ++digit; 17 } 18 19 return digit; 20 } 21 22 int GetReminder(int value,int digit) 23 { 24 int div=1; 25 for(int i=1;i<digit;++i) 26 div*=10; 27 28 return value/div%10; 29 } 30 31 void RRadixSort_MSD(int* h, int begin, int end, int digit) 32 { 33 if(h==NULL) return; 34 if(begin>=end) return; 35 if(digit<1) return; 36 37 int start[10]; 38 int count[10]={0}; 39 int *tmp=(int*)calloc(end-begin+1,sizeof(int)); 40 41 for(int i=begin;i<=end;++i) 42 { 43 count[GetReminder(h[i],digit)]++; 44 } 45 46 memcpy(start,count,sizeof(start)); 47 48 //求右边界 49 for(int i=1;i<10;++i) 50 { 51 start[i]+=start[i-1]; 52 } 53 54 for(int i=end;i>=begin;--i) 55 { 56 int r=GetReminder(h[i],digit); 57 int index=start[r]; 58 tmp[index-1]=h[i]; 59 start[r]--; 60 } 61 62 /* 63 for(int i=0;i<10;++i) 64 { 65 printf("%d ",start[i]); 66 } 67 68 printf("\n"); 69 */ 70 71 memcpy(&h[begin],tmp,(end-begin+1)*sizeof(int)); 72 73 for(int i=0;i<10;++i) 74 { 75 if(count[i]>1) 76 { 77 RRadixSort_MSD(h, start[i], start[i]+count[i]-1, digit-1); 78 } 79 } 80 } 81 82 void RadixSort_MSD(int* h, int len) 83 { 84 if(h==NULL) return; 85 if(len<=1) return; 86 87 int digit=GetMaxDight(h,len); 88 89 //printf("MaxDigit:%d\n",digit); 90 91 RRadixSort_MSD(h, 0, len-1, digit); 92 } 93 94 void RRadixSort_MSD_Reverse(int* h, int begin, int end, int digit) 95 { 96 if(h==NULL) return; 97 if(begin>=end) return; 98 if(digit<1) return; 99 100 int start[10]; 101 int count[10]={0}; 102 int *tmp=(int*)calloc(end-begin+1,sizeof(int)); 103 104 for(int i=begin;i<=end;++i) 105 { 106 count[GetReminder(h[i],digit)]++; 107 } 108 109 memcpy(start,count,sizeof(start)); 110 111 //求右边界 112 for(int i=8;i>=0;--i) 113 { 114 start[i]+=start[i+1]; 115 } 116 117 for(int i=end;i>=begin;--i) 118 { 119 int r=GetReminder(h[i],digit); 120 int index=start[r]; 121 tmp[index-1]=h[i]; 122 start[r]--; 123 } 124 125 /* 126 for(int i=0;i<10;++i) 127 { 128 printf("%d ",start[i]); 129 } 130 131 printf("\n"); 132 */ 133 134 memcpy(&h[begin],tmp,(end-begin+1)*sizeof(int)); 135 136 for(int i=0;i<10;++i) 137 { 138 if(count[i]>1) 139 { 140 RRadixSort_MSD_Reverse(h, start[i], start[i]+count[i]-1, digit-1); 141 } 142 } 143 } 144 145 void RadixSort_MSD_Reverse(int* h, int len) 146 { 147 if(h==NULL) return; 148 if(len<=1) return; 149 150 int digit=GetMaxDight(h,len); 151 152 //printf("MaxDigit:%d\n",digit); 153 154 RRadixSort_MSD_Reverse(h, 0, len-1, digit); 155 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
算法比较
