激光SLAM从理论到实践学习——第六节（基于图优化的激光SLAM方法）_基于图优化的slam算法

基于图优化的激光SLAM方法（Grid-based栅格地图）

• 之前说的都是基于滤波器的，典型的就是gmapping算法

  在估计的时候只是估计当前的位置xt，那么一旦x0:t-1中间出现错误的话，那么估计xt出错的可能性就会越来越大。

• 基于滤波器的算法每次估计的是xt，当前时刻的位姿。而图优化估计的是x0:t，估计的是一个轨迹，轨迹上的每一个位姿都会进行估计，假设当你在某点出现一个很大的误差的时候，那么当他回到误差点的时候他可以对这个误差进行消除。

• 图优化最终的求解是要用到非线性最小二乘法。

Graph-base SLAM

Graph-base SLAM把SLAM分为两部分，前端和后端。前端构图（帧间匹配，回环检测），后端优化。用图来表示SLAM的问题，图中节点表示机器人的位姿，两个节点之间的边表示两个位姿的空间约束。

Graph-base SLAM：构建图，并找到一个最优的配置（机器人在各节点中的位姿），让里程计预测值与激光雷达的观测值的误差最小（最小二乘）。注意他是各节点中的位姿，也就是说x1到t时刻的位姿都需要找。

非线性最小二乘原理(二乘就是误差的平方和)

• 需要解决的问题

  

  • 给定一个系统，其状态方程由f(x)=z描述。其中：x为该系统的状态向量（即需要估计的值，在激光SLAM中就是机器人的位姿）、f(x)是一个非线性的映射函数、状态向量x，可以通过非线性函数f(x)映射得到z1预测值，z表示系统的观测值，可以通过传感器进行直接观测（激光雷达的值）。

  • 给定该系统的n个混有噪声的观测值(z1,⋯,zn)，估计状态向量x，使得其经过f(x)映射之后的预测值和观测值的误差最小。

    我们已知zi激光雷达的观测值了，现在假设预测值为z1，我们要做的就是估计状态向量x，使得||z1-zi||最小（预测值与观测值误差最小）

  • 跟线性最小二乘基本相同，不同之处在于f(x)是一个非线性函数

• 示意图

  

  看图可知，x是状态量，是机器人的位姿。f(x)是传感器的观测模型，或者说观测函数，求解这个观测函数就可以得到预测值z1。z是传感器的观测值，一般就是激光数据。||z1-z||表示的是预测值与观测值的误差，目的就是找到最优的x，让这个误差最小。

• 误差函数

  

  • 目标我们已经知道了，就是最小化预测值和观测值的差，因此误差即为预测值与雷达数据观测值的差为：

    ei(x) = fi(x) - zi

  • 假设误差服从高斯分布，因此其对应的信息矩阵为∑i，因此该预测值与观测值的误差的平方定义为：

    Ei(x) = ei(x)T∑iei(x)

    注：向量的平方是其转置矩阵。

    ​ 每个观测值都有不同的可靠性，因此用的是一个加权最小二乘，所有存在一个信息矩阵∑i（权重矩阵）来进行加权。

  • 因此，非线性最小二乘的目标函数就是

    误差的平方和，也就是我们要找到一个x，使得这个目标函数最小。当然，目标函数F(x)是非线性的，是因为ei(x)是非线性的（实际是因为ei(x)计算中的fi(x)是非线性的）。

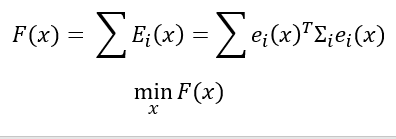
• 解决的问题：

  

  • 我们的直接想法就是跟线性一样，求目标函数关于变量x的导数，令其等于0，求解方程即可。但是这样对于非线性问题是行不通的。
  • F(x)为关于x的非线性方程，能否把其化为关于x的线性方程？是可以的，线性化只需要对其进行泰勒展开（所有线性化的工程问题基本都是用的泰勒展开）。

• 线性化

  

  • F(x)是关于x的非线性函数的原因是，误差函数ei(x)是一个非线性函数（ei(x)中的f(x)），他是引起系统非线性的原因。因此直接对误差看书ei(x)进行线性化即可。泰勒展开有：

    

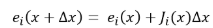
    其中J为映射函数对状态向量x的导数，称之为Jacobian矩阵（雅克比矩阵）。

    

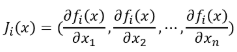
    因此函数F(x)可化简为：

    

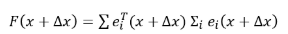
  • F(x)的化解

    

    首先进行分别相乘，得到第三步，然后化简结合得到第四步和第五步

  • 得到解

    

  • 求解

    

    2b+2H△x=0是一个适定方程组（未知数个数和方程个数相等），所以不能用最小二乘来求。

  • 流程

    • 1.对误差函数进行线性化
    • 2.构建一个线性系统
    • 3.求解线性系统
    • 4.更新解，并不断迭代直至收敛

非线性最小二乘原理总结

x是状态量，是机器人的位姿。f(x)是传感器的观测模型或者说观测函数，求解这个观测函数就可以得到预测值z1。z是传感器的观测值，一般就是激光数据。 ||z1-z||表示的是预测值与观测值的误差，目的就是找到最优的x，使得f(x)预测值与雷达观测值的误差最小。

非线性最小二乘在图优化SLAM中的应用

• SLAM前端：图的构建

  ​

  • 构建地图的边方式分为两种：

    • 第一种是里程计测量构建边

      机器人从节点xi运动到节点xi+1，里程计测量得到此运动信息。并在对应的节点中连上一条边，边为里程计测量值。

    • 第二种是回环检测构建边

      节点xi和节点xj观测到同样的环境信息（比较多的重合），那么两者进行匹配得到相对位姿。并在对应的节点中连一条边，边为匹配的相对位姿。用信息矩阵来描述本次匹配的可靠性。

• SLAM后端：进行优化

  

  • 误差函数

    • 观测值zij=(dx,dy,dθ)表示经过匹配计算得到节点xi和节点xj的相对位姿。节点xj在节点xi坐标系下的坐标。
    • 预测值为里程计的测量值，图中xi和xj即为里程计测量得到的坐标，因此预测值z1ij = Xi-1Xj,其中Xi表示xi对应的转换矩阵。
    • 因此误差函数eij(x) = t2v(Zij-1Z1ij)。t2v表示把转换矩阵转换到对应的位姿。

  • 误差函数的形式

    写出误差函数的矩阵形式后，就要写出对应的贾科比矩阵，知道贾科比矩阵后就可以进行线性化了。

    

  • 误差函数的线性化

    

    

    

  • 固定坐标系

    观测值观测到的值是两个位姿之间的相对位姿。

    

    

  • 构建线性系统

    

  • 求解

    已知矩阵H和向量b，求解线性方程组，不断进行迭代，直至收敛。

    

Cartographer介绍

• 基于图优化的SLAM算法
• 有比较完善的匹配系统，包含建图和定位
• 目前效果最好的开源激光SLAM系统
• 有人在专门的维护，不断增加新的特性。

作业：实现一个高斯牛顿进行Pose-Graph的优化