繁依Fanyi0

这个屌丝很懒，什么也没留下！

热门标签

阅读笔记-Effective Capacity Analysis of STAR-RIS-Assisted NOMA Networks

作者：繁依Fanyi0 | 2024-03-23 22:33:28

踩

star-ris

STAR-RIS：即同时折射和反射可重构智能表面（simulta-neously transmitting and reflecting reconfigurable intelligent sur-face）

EC:为满足服务质量的要求所能维持的最大恒定可实现服务速率

1 摘要

本文研究了同时折射和反射的可重构智能表面(STAR-RIS)辅助非正交多址(NOMA)网络的性能，以支持超可靠的低延迟通信。采用有效容量(EC)作为度量来探索NOMA用户的延迟需求。具体而言，得到了分布于STAR-RIS的一对NOMA用户的网络的EC解析表达式。此外，在高性噪比斜率和高信噪比功率偏置下对EC进行渐进分析，数值结果表明：

（1）在高信噪比下，近用户(Un)的电子辐射系数呈线性增加，远用户(Um)的电子辐射系数趋于常数

（2）STAR-RIS 的使用提高了NOMA网络中Un和整个网络的EC。

（3）增加STAR-RIS元素的数量是改善Un和Um EC的有效策略。

2 系统模型

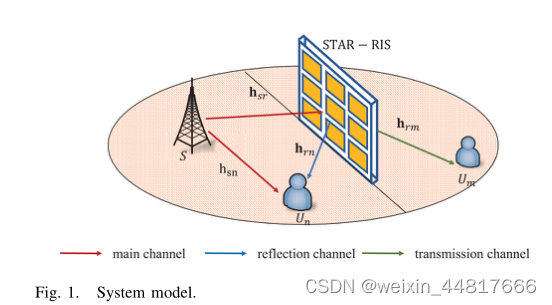
2.1 信道

本文为了刻画信道的统计特性，设定所有信道均为Nakagami-M衰落，并且假设所有用户均为单天线设备。

2.2信号

本文的模型中仅有对一单天线用户（近用户和远用户）

近用户接收到的信号：

远用户接收到的信号：

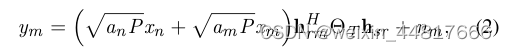
P为基站S的发射功率， $a_{n}$ , $a_{m}$ 分别为功率分配系数，并满足 $a_{n}$ < $a_{m}$ ,且 $a_{n}$ + $a_{m}$ =1， $\Theta _{T}$ 和 $\Theta _{R}$ 分别为star-ris的折射和反射系数矩阵， $n_{n}$ 和 $n_{m}$ 为加性高斯白噪声

2.3用户位置

（1）近NOMA（Un）用户位于star-ris的正面，不仅可以接收基站S的信号，也可接受star-ris的反射信号

（2）远NOMA(Um)用户只能接受star-ris的折射信号

（3）hsr、hrn、hsn和hrm分别表示S−RIS、RIS−Un、S−Un和RIS−Um的信道系数（通信链路），所有信道均满足Nakagami-M分布，即hsn∼Nakagami(msn, 1)， hsr∼Nakagami(msr, 1)， hrn∼Nakagami(mrn, 1)和hrm∼Nakagami(mrm, 1)，其概率密度分布函数为

其中，为平均功率，为伽马函数，m为衰落参数。m=1时，上式退化为瑞利衰落；并且若一个随机变量是服从Nakagami-m分布的，那么它的模值的平方服从伽马分布，即：若是服从衰落参数为的Nakagami-m分布，则有，且的PDF（概率密度分布函数）为：

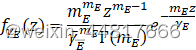
2.4信干噪比

（1）Un（近用户）首先解码Um的信号，然后采用SIC消除Um的信号解码自己的信号，过程如下

$\gamma_{n \rightarrow m}=\frac{\rho a_m\left|h_{s n}+\mathbf{h}_{r n}^H \Theta_R \mathbf{h}_{s r}\right|^2}{\rho a_n\left|h_{s n}+\mathbf{h}_{r n}^H \Theta_R \mathbf{h}_{s r}\right|^2+1}$

$\gamma_n=\rho a_n\left|h_{s n}+\mathbf{h}_{r n}^H \Theta_R \mathbf{h}_{s r}\right|^2$

（2）Um（远用户）直接解码自己的信号

$\gamma_m=\frac{\rho a_m\left|\mathbf{h}_{r m}^H \Theta_T \mathbf{h}_{s r}\right|^2}{\rho a_n\left|\mathbf{h}_{r m}^H \Theta_T \mathbf{h}_{s r}\right|^2+1}$

其中ρ为基站S发射信号的信噪比（SNR）

3 性能分析

3.1.Un的EC的表达式为：

$\mathcal{R}_n=-\frac{1}{A} \log _2\left(\int_0^{\infty}\left(1+\gamma_n\right)^{-A} f\left(\gamma_n\right) d_{\gamma_n}\right)$

，由于上式积分很难计算，故在本文作者提出了一种近似方法，具体过程不在此详细描述，可得:

$R_n=-\frac{1}{A} \log _2\left(\frac{\frac{\Gamma\left(k_Z-A\right)}{\Gamma\left(k_Z\right)} \sum_{k=0}^{\infty} \frac{(A)_k\left(\rho a_n \theta_Z\right)^{-k}}{\left(A+1-k_Z\right)_k k !}+\frac{\Gamma\left(A-k_Z\right)}{\Gamma(A)} \sum_{k=0}^{\infty} \frac{\left(k_Z\right)_k\left(\rho a_n \theta_Z\right)^{-k+A-k_Z}}{\left(1-A+k_Z\right)_k k !}}{\left(\rho a_n \theta_Z\right)^{2 k_Z+1-A}}\right)$

其中A≜θTB/ln⁡2，T和B分别为块衰落信道的长度和带宽， $k_Z=\frac{\mu_Z^2}{\mu_Z^{(2)}-\mu_Z^2}$ ， $\theta_Z=\frac{\mu_Z^{(2)}-\mu_Z^2}{\mu_Z}$ ，

若在在高信噪比条件下，，我们可以用高信噪比功率和高信噪比功率偏移量来对Un的EC进行表征，并可得Un的EC的渐进表达式为：

$\mathcal{R}(\rho, \theta)=\mathcal{S}_{\infty}\left(\log _2 \rho-\mathcal{L}_{\infty}\right)+o(1)$

其中 $\mathcal{S}_{\infty}$ 为高信噪比斜率， $\mathcal{L}_{\infty}$ 为3dB高信噪比功率偏移量， $o(1)$ 为无穷小， $\theta$ 为延迟中断概率，并由原文可知 $\mathcal{S}_{\infty}$ 和 $\mathcal{L}_{\infty}$ 的计算方式如下：

$\mathcal{S}_{\infty}=\lim _{\rho \rightarrow \infty} \frac{\mathcal{R}(\rho, \theta)}{\log _2 \rho}$ ， $\mathcal{L}_{\infty}=\lim _{\rho \rightarrow \infty}\left(\log _2 \rho-\frac{\mathcal{R}(\rho, \theta)}{\mathcal{S}_{\infty}}\right)$

通过计算和分析可得：在star-ris辅助NOMA网络中，Un的高信噪比斜率和高信噪比功率偏移为： $\mathcal{S}_{\infty}^n= \begin{cases}\frac{k_Z-A}{A}, & A \leq k_Z \\ \frac{k_Z}{A}, & A>k_Z\end{cases}$ ， $\mathcal{L}_{\infty}^n=\infty$

3.2.Um的EC表达式为：

$\mathcal{R}_m=-\frac{1}{A} \log _2\left(\int_0^{\infty}\left(1+\gamma_m\right)^{-A} f\left(\gamma_m\right) d_{\gamma_m}\right)$ ，

由于上式积分也很难计算，故原文中采用的是通过给出 $\gamma_m$ 的PDF（概率密度表达式），然后进行近似计算，最终可得Um的EC的解析表达式：

$R_m=-\frac{1}{A} \log _2\left(\sum_{j=0}^{\infty} \sum_{q=0}^{\infty} \sum_{t=0}^{\infty} \frac{e^{-\frac{\lambda}{2}}\left(\frac{\lambda}{2}\right)^j(-1)^q a_m \Gamma\left(j+q+\frac{3}{2}+t\right) \Gamma(1+A+t)\left(1+\frac{a_m}{a_n}\right)^t\left(-a_n\right)^{-j-q-\frac{3}{2}}}{j ! \Gamma\left(j+\frac{1}{2}\right)^j q !\left(2 L_m \rho(1-\xi)\right)^{\frac{1}{2}+j+q}\left(j+q+\frac{1}{2}\right) \Gamma\left(A+j+q+\frac{3}{2}+t\right) t !}\right)$

其中 $L_m$ 为star-ris中用于折射的元素数量， $\Gamma(\cdot)$ 则代表的是伽马函数，

$\lambda=\frac{L_m \xi}{1-\xi}$ ， $\frac{\left(\Gamma\left(m_{r m}+\frac{1}{2}\right) \Gamma\left(m_{s r}+\frac{1}{2}\right)\right)^2}{m_{r m} m_{s r}\left(\Gamma\left(m_{r m}\right) \Gamma\left(m_{s r}\right)\right)^2}$ ，其中 $m_{r m}$ ， $m_{s r}$ ， $m_{s r}$ 为各衰落信道的衰落参数。

和Un相同，在高信噪比条件下可以用高信噪比斜率和高信噪功率偏移量来对Um的EC进行表征，并可得Um的高信噪比斜率和高信噪功率偏移量分别为： $\mathcal{S}_{\infty}^m=0$ ， $\mathcal{L}_{\infty}^m=\infty$ 。

3.3.通过两者的EC表达式进行分析可得：

(1)EC与信道参数、QoS指数、功率分配系数和发射功率有关;

(2)在高信噪比下，Un的EC随发射功率线性增加，Um的EC保持不变;

4 仿真

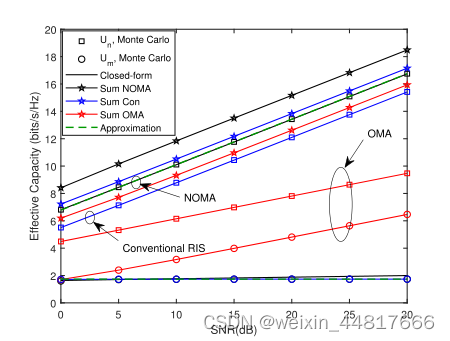
上图证明了刚才在STAR-RIS N辅助OMA网络情况下为EC推导的表达式的准确性。第一点是在相同信噪比下，Un的EC性能优于Um。在ρ值高的地区，Un的这种优势更加突出。

详细描述:Un随ρ线性增加，Um随ρ增加收敛为常数，与分析结论一致。产生这些结果的原因是在NOMA情况下Un具有SIC的优势，与Um相比具有更大的SINR值。ρ→∞，γn→∞，γm→am/an。此外，为了比较OMA和NOMA情况下STAR-RIS的ECs，我们用红色曲线提供了OMA情况下所有用户和全网的EC曲线。从图中可以看出，Un和Um的ECs都随着 $\rho$ 单调增加，并与NOMA相比，Um的EC性能提高，Un的EC性能下降。并且很明显可以看出，对于STAR-RIS网络，NOMA情况下系统和EC较高，这意味着NOMA有利于提高STAR-RIS网络的EC。此外，与传统RIS网络的对比如图所示，蓝色曲线。传统的RIS网络是用两个RISs来说明的，每个RISs有20个元素，一个用于反射，另一个用于传输。可以注意到Un比传统RIS的EC较高，而Um与传统RIS网络相比差异不是很明显。其次，对于整个系统而言，STAR-RIS NOMA网络的EC显著大于常规RIS网络，即STAR-RIS NOMA网络可以根据实际情况调整反射和/或发射单元的数量，从而获得更高的性能。

除此之外作者还对QoS指数θ指数对有效容量EC的影响，star-ris 的元素数量对EC的影响进行了仿真，具体过程类似不在详细描述，最终的出结论为：

(1)θ越大意味着QoS延迟要求越严格，将导致EC越小,当θ增大时，Un和Um的ECs均有不同程度的下降，其中Un的下降更为明显。

(2)当STAR-RIS的元素数量较小时，ρ值对Um的EC影响较大。而当STAR-RIS的元素数增加到一定值时，Um的EC不再随着STAR-RIS的元素数增加，因为当Lm→∞，γm→am/an

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/298116