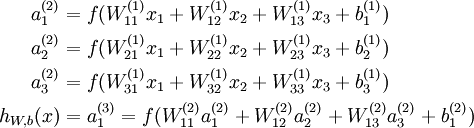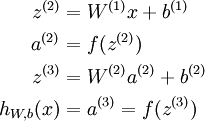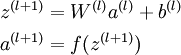- 1华为官方推荐:学习鸿蒙开发高分好书,这6本能帮你很多!_鸿蒙开发 推荐 书籍
- 2ELF文件中得section(.data .bss .text .altinstr_replacement、.altinstr_aux)_.section .datar, data
- 3ssm的maven坐标_ssm maven 坐标
- 4MySQL存储引擎详解(一)-InnoDB架构_mysql引擎innodb
- 5(一)使用AI、CodeFun开发个人名片微信小程序_ai生成小程序代码
- 6求助:R包安装失败_cannot open compressed file description
- 74款超好用的AI换脸软件,一键视频直播换脸(附下载链接)
- 8【深度学习】激活函数(sigmoid、ReLU、tanh)_sigmoid激活函数
- 9操作系统的程序内存结构 —— data和bss为什么需要分开,各自的作用_为什么分bss和data
- 10记一次 Docker Nginx 自定义 log_format 报错的解决方案_log_format" directive no dyconf_version config in
神经网络模型符号解释!!!蛮重要的,记不住的可以参考下。_图神经框图中一个圆圈一个叉什么意思
赞
踩
神经网络模型符号解释!!!蛮重要的,记不住的可以参考下。
神经网络模型符号解释!!!蛮重要的,记不住的可以参考下。
神经网络模型
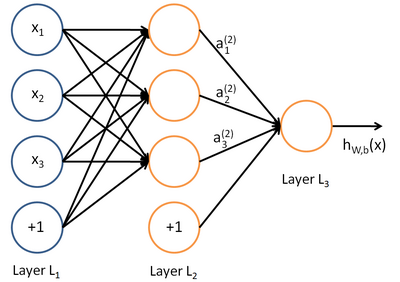
所谓神经网络就是将许多个单一“神经元”联结在一起,这样,一个“神经元”的输出就可以是另一个“神经元”的输入。例如,下图就是一个简单的神经网络:
我们使用圆圈来表示神经网络的输入,标上“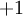 ”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
我们用 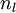 来表示网络的层数,本例中
来表示网络的层数,本例中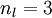 ,我们将第
,我们将第 层记为
层记为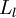 ,于是
,于是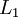 是输入层,输出层是
是输入层,输出层是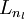 。本例神经网络有参数
。本例神经网络有参数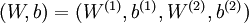 ,其中
,其中 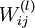 (下面的式子中用到)是第
(下面的式子中用到)是第 层第
层第 单元与第
单元与第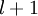 层第
层第 单元之间的联接参数(其实就是连接线上的权重,注意标号顺序),
单元之间的联接参数(其实就是连接线上的权重,注意标号顺序),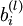 是第
是第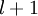 层第
层第 单元的偏置项。因此在本例中,
单元的偏置项。因此在本例中,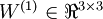 ,
,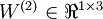 。注意,没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出
。注意,没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出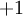 。同时,我们用
。同时,我们用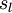 表示第
表示第 层的节点数(偏置单元不计在内)。
层的节点数(偏置单元不计在内)。
我们用 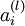 表示第
表示第 层第
层第 单元的激活值(输出值)。当
单元的激活值(输出值)。当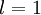 时,
时,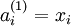 ,也就是第
,也就是第 个输入值(输入值的第
个输入值(输入值的第 个特征)。对于给定参数集合
个特征)。对于给定参数集合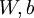 ,我们的神经网络就可以按照函数
,我们的神经网络就可以按照函数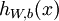 来计算输出结果。本例神经网络的计算步骤如下:
来计算输出结果。本例神经网络的计算步骤如下:
我们用 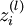 表示第
表示第 层第
层第 单元输入加权和(包括偏置单元),比如,
单元输入加权和(包括偏置单元),比如, 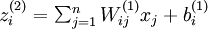 ,则
,则 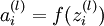 。
。
这样我们就可以得到一种更简洁的表示法。这里我们将激活函数 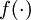 扩展为用向量(分量的形式)来表示,即
扩展为用向量(分量的形式)来表示,即![\textstyle f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]](http://deeplearning.stanford.edu/wiki/images/math/d/b/8/db84346dcd6187f0fbb0f6c1a72eecf8.png) ,那么,上面的等式可以更简洁地表示为:
,那么,上面的等式可以更简洁地表示为:
我们将上面的计算步骤叫作前向传播。回想一下,之前我们用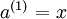 表示输入层的激活值,那么给定第
表示输入层的激活值,那么给定第 层的激活值
层的激活值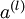 后,第
后,第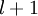 层的激活值
层的激活值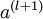 就可以按照下面步骤计算得到:
就可以按照下面步骤计算得到:
将参数矩阵化,使用矩阵-向量运算方式,我们就可以利用线性代数的优势对神经网络进行快速求解。
以上内容参考了AG的文献,加上个人的理解!希望可以帮助到大家~