TimesNet

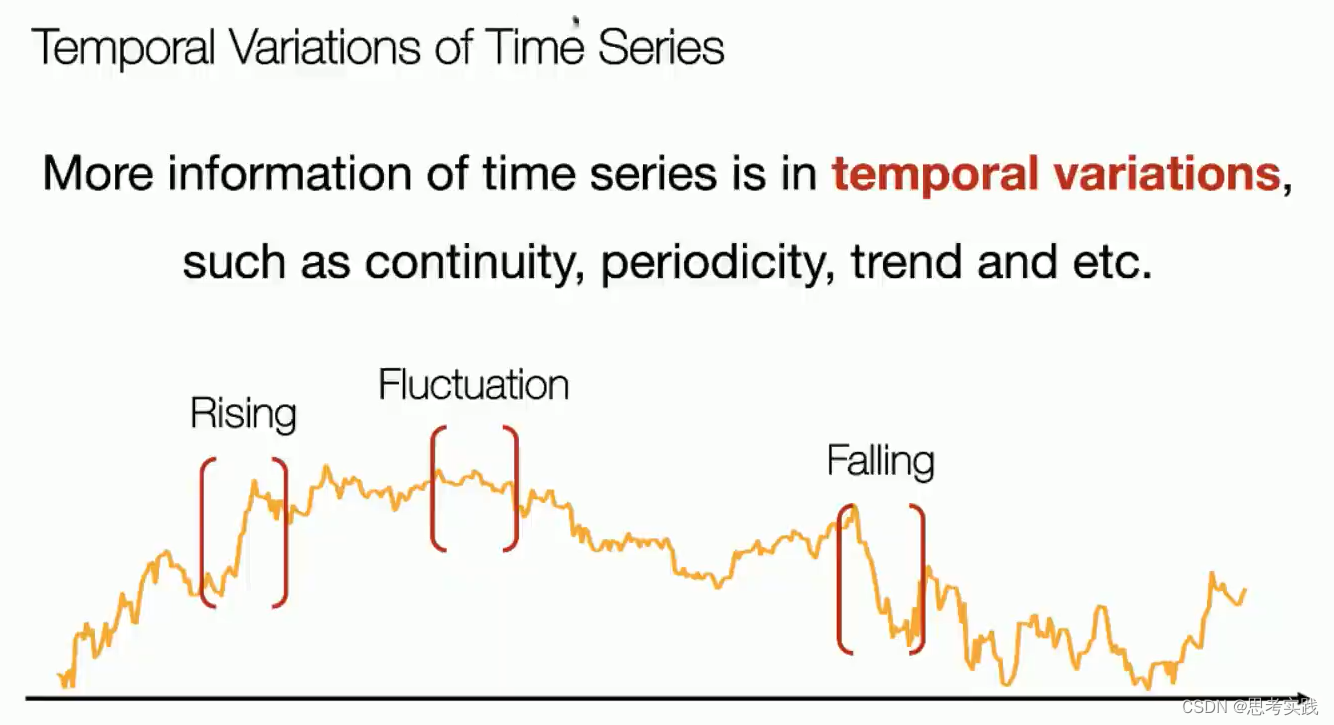
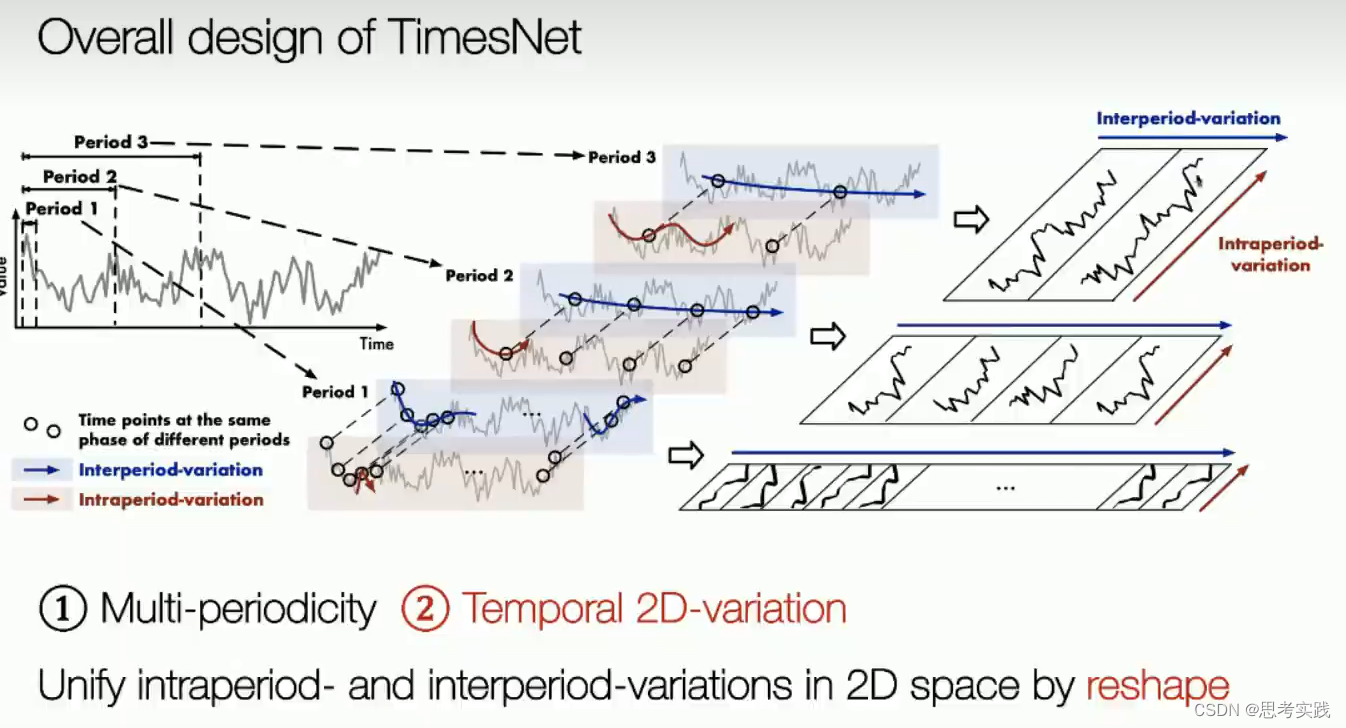
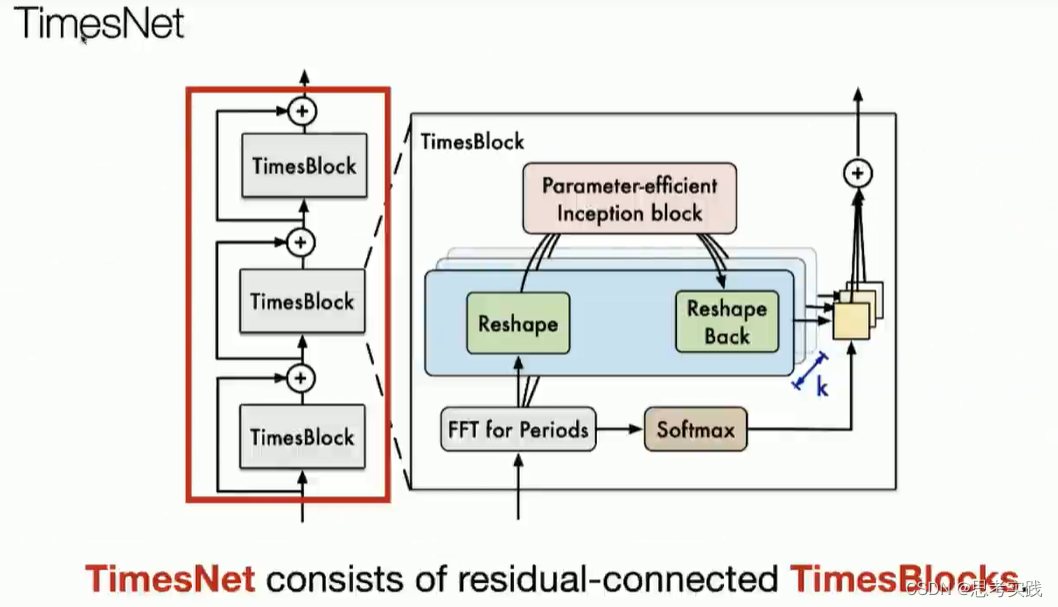
每一行代表不同周期同相位的过程。 每一列代表同周期内的一个变换，这样子我们就可以把这个interperiod和interperiod 两个variation在2d空间里面实现了一个统一，那这样的结构对于我们的分析，也是非常有帮助的，我们这里有个小case，我们把Electricity这个数据集重新，我们按照上面这种reshape方法把它去重新组织一下，然后这个纸这个颜色的深浅，代表这个数值的大小，我们会发现组织出来的这个呃time series已经具有了一定的啊特殊的性质对吧，它具有一定的locality,所谓locality就是说它有一定的局部性，这种局部性其实是我们呃所有这个当前的这个视觉领域的分析的一些基础的，就是你你基于这个image它具有一定的局局部性，所以你才可以用卷积网络去处理它，那对应的呢这种局部性的启发，我们去啊做一个非常简单的操作了

 就是说首先呢啊我们把1d-time series编到2d空间,然后紧接着我们就可以通过2d kernel,就是说我们可以通过2d-kernel去处理这个time series，因为以前的话大家都在1d空间里面去分析，你会发现1d-kernel这个感受野比较小，就是说它这个你也没办法去捕捉这个间隔的信息嘛，但是当我们把它重新组织完之后，我们可以通过2d卷积非常轻松的去捕捉出它这个周期内和周期间的变化了，当然还有一个隐式的优势，因为我们知道卷积非常快，然后你把它reshift完之后，比如说啊我们一个长度是1W的一个时间序列，reshape完之后可能就变成100x100了，那咱这当然这是理想情况，但我们知道100x100对于image来说是一个非常好、非常小的image,也就是说我们把一个程序列变成了一个在2d空间上，把它变成一个变成一个非常小的一个二维空间里面的tensor，这个过程就变得非常快，

 然后啊就以上就是我们这个timesnet一些motivation，首先是①多周期视角②Temporal 2D-variation的建模。

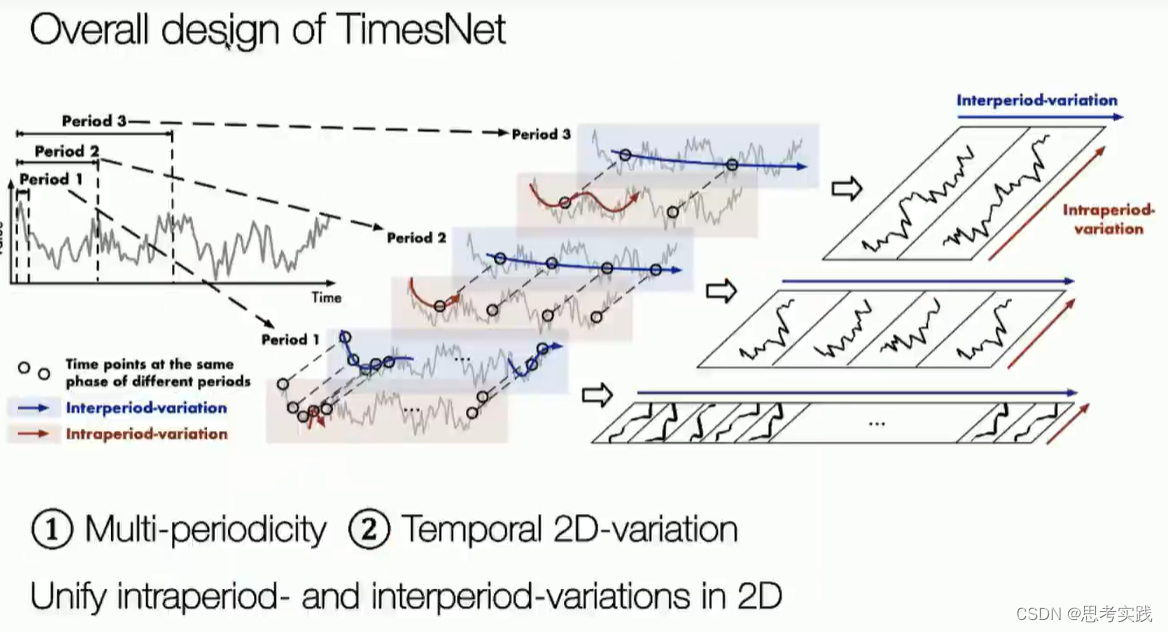
 然后接下来就是去设计这个type series,

Key Points

1D变2D

这是本文的核心。大部分现有方法都是作用于时间序列的时间维度，捕获时序依赖性。实际上，现实时间序列一般都有多种模式，比如不同的周期，各种趋势，这些模式混杂在一起。如果直接对原始序列的时间维度来建模，真正的时序关系很可能隐藏在这些混杂的模式中，无法被捕获。考虑到：现实世界的时间序列通常具有多周期性，比如每天周期、每周周期、每月周期；而且，每个周期内部的时间点是有依赖关系的（比如今天1点和2点），不同的相邻周期内的时间点也是有依赖关系的（比如今天1点和明天1点），作者提出将1D的时间维度reshape成2D的，示意图如下。下图左侧的时间序列具有三个比较显著的周期性（Period 1、Period 2、Period 3），将其reshape成三种不同的2D-variations，2D-variations的每一列包含一个时间段（周期）内的时间点，每一行包含不同时间段（周期）内同一阶段的时间点。变成2D-variations之后，就可以采用2D卷积等方式来同时捕获时间段内部依赖和相邻时间段依赖。

为了确定时间序列中的周期性，可以使用傅里叶变换来分析其频率成分。通过对时间序列进行傅里叶变换后，可以得到不同频率的复数值，并且主要周期对应的频率成分通常具有高振幅，即高幅值。因此，可以选择取最大的k个幅值对应的频率成分来确定top k个主要的周期。类似于Autoformer中的处理方式。

具体操作如下图所示。首先，从所有频率成分中选择top k个幅值最大的成分，以此确定top k个主要周期。在此只画了三个周期作为示例。然后，将原始1D时间序列reshape成三种不同的2D形式（如果不能整除，则可以使用padding），并对这三种2D形式的序列分别采用2D卷积进行处理，最后聚合处理结果即可得到时间序列的周期性特征。

需要注意的是，在实际应用中，可能需要根据具体问题对top k的值进行调整，并对选取的周期进行更深入的分析。

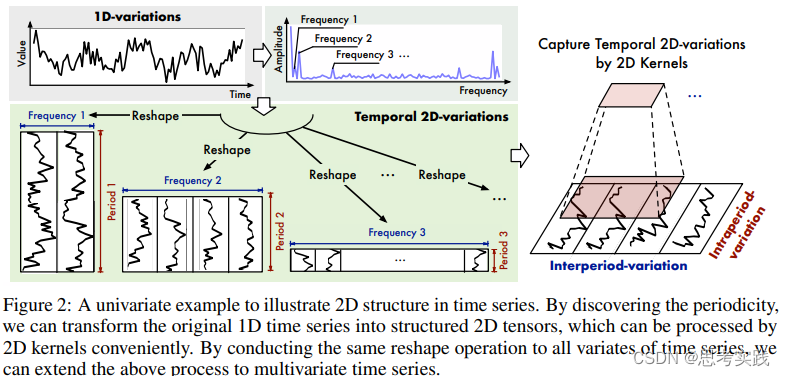
 这一步需要看代码搞懂具体怎么变换的。

为了直观理解2D变化，我们在图9中展示了转换后的2D张量。根据可视化结果，我们可以得到以下观察结果：

• 交替周期变化能够呈现时间序列的长期趋势。例如，在Exchange数据集的第一个例子中，每行的值从左到右递减，表明原始序列的下降趋势。而对于ETTh1数据集，每行的值相互类似，反映了原始序列的全局稳定变化。（这个ETTh1这个的说法我不太完全赞同，因为数据集Exchange与ETTh1分别如图所示，ETTh1怎么会稳定呢？）

Exchange:

ETTh1:

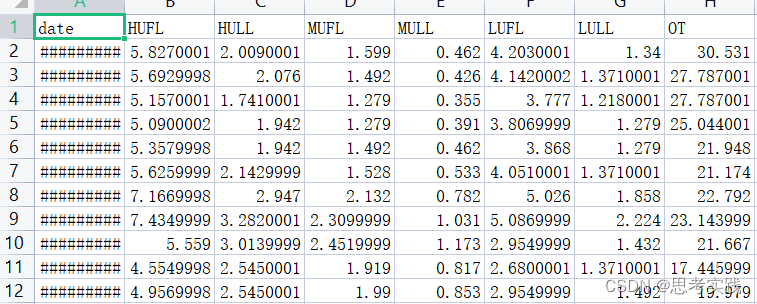
• 对于没有明显周期性的时间序列，时间上的2D变化仍然可以呈现有用的2D结构。如果频率为一，则交替周期变化就是原始序列的变化。此外，交替周期变化也可以呈现长期趋势，有益于时间变化建模。

• 转换后的2D变化展示了两种类型的局部性。首先，对于每一列（周期内变化），相邻的值彼此接近，呈现出相邻时间点之间的局部性。其次，对于每一行（交替周期变化），相邻的值也很接近，对应于相邻周期之间的局部性。请注意，非相邻周期之间可能差异很大，这可能是由于全局趋势造成的，例如来自Exchange数据集的情况。这些局部性的观察结果也激发了我们采用2D卷积进行表示学习的想法。

模型代码：Time-Series-Library/TimesNet.py at main · thuml/Time-Series-Library · GitHub

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.fft
from layers.Embed import DataEmbedding
from layers.Conv_Blocks import Inception_Block_V1
 
 
def FFT_for_Period(x, k=2):
    # [B, T, C]
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    '''
    这行代码计算了每个频率成分在所有时间步和通道上的平均幅值，返回一个长度为T/2+1的tensor。具        
   体地，首先使用abs函数计算xf的绝对值，然后在dim=0上取平均值（即对所有样本取平均），再在 
    dim=-1上取平均值（即对所有通道取平均）。结果是一个形状为[T/2+1]的tensor，其中第一个元素代 
     表直流成分，即对应于0 Hz的频率成分。
    '''
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]
'''
这段代码使用FFT来找出时间序列中的主要周期，并返回top k个周期对应的幅值。
输入参数x是一个形状为[B, T, C]的tensor，分别表示batch size、时间步和通道数。
在该函数中，通过使用torch.fft.rfft来进行实数快速傅里叶变换，得到频域复数张量xf [B, T/2+1, C]。
然后，计算各个频率成分的平均幅值，将第一个元素设为0（代表直流成分），并使用torch.topk函数找到前k个最大幅值对应的频率成分（即top k个周期）。
对于每个找到的周期，计算其在时间轴上的长度（即时间步数）并返回周期列表。
同时，选择top k个周期对应的频率成分，并返回它们在每个样本通道上的幅值。
'''
 
class TimesBlock(nn.Module):
    def __init__(self, configs):
        super(TimesBlock, self).__init__()
        self.seq_len = configs.seq_len
        self.pred_len = configs.pred_len
        self.k = configs.top_k
        # parameter-efficient design
        self.conv = nn.Sequential(
            Inception_Block_V1(configs.d_model, configs.d_ff,
                               num_kernels=configs.num_kernels),
            nn.GELU(),
            Inception_Block_V1(configs.d_ff, configs.d_model,
                               num_kernels=configs.num_kernels)
        )
 
    def forward(self, x):
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)
 
        res = []
        for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = (
                                 ((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = (self.seq_len + self.pred_len)
                out = x
            # reshape
            out = out.reshape(B, length // period, period,
                              N).permute(0, 3, 1, 2).contiguous()
            # 2D conv: from 1d Variation to 2d Variation
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            res.append(out[:, :(self.seq_len + self.pred_len), :])
        res = torch.stack(res, dim=-1)
        # adaptive aggregation
        period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        res = res + x
        return res
 
 
class Model(nn.Module):
    """
    Paper link: https://openreview.net/pdf?id=ju_Uqw384Oq
    """
 
    def __init__(self, configs):
        super(Model, self).__init__()
        self.configs = configs
        self.task_name = configs.task_name
        self.seq_len = configs.seq_len
        self.label_len = configs.label_len
        self.pred_len = configs.pred_len
        self.model = nn.ModuleList([TimesBlock(configs)
                                    for _ in range(configs.e_layers)])
        self.enc_embedding = DataEmbedding(configs.enc_in, configs.d_model, configs.embed, configs.freq,
                                           configs.dropout)
        self.layer = configs.e_layers
        self.layer_norm = nn.LayerNorm(configs.d_model)
        if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
            self.predict_linear = nn.Linear(
                self.seq_len, self.pred_len + self.seq_len)
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
        if self.task_name == 'imputation' or self.task_name == 'anomaly_detection':
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
        if self.task_name == 'classification':
            self.act = F.gelu
            self.dropout = nn.Dropout(configs.dropout)
            self.projection = nn.Linear(
                configs.d_model * configs.seq_len, configs.num_class)
 
    def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):
        # Normalization from Non-stationary Transformer
        means = x_enc.mean(1, keepdim=True).detach()
        x_enc = x_enc - means
        stdev = torch.sqrt(
            torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
        x_enc /= stdev
 
        # embedding
        enc_out = self.enc_embedding(x_enc, x_mark_enc)  # [B,T,C]
        enc_out = self.predict_linear(enc_out.permute(0, 2, 1)).permute(
            0, 2, 1)  # align temporal dimension
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))
        # porject back
        dec_out = self.projection(enc_out)
 
        # De-Normalization from Non-stationary Transformer
        dec_out = dec_out * \
                  (stdev[:, 0, :].unsqueeze(1).repeat(
                      1, self.pred_len + self.seq_len, 1))
        dec_out = dec_out + \
                  (means[:, 0, :].unsqueeze(1).repeat(
                      1, self.pred_len + self.seq_len, 1))
        return dec_out
 
    def imputation(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask):
        # Normalization from Non-stationary Transformer
        means = torch.sum(x_enc, dim=1) / torch.sum(mask == 1, dim=1)
        means = means.unsqueeze(1).detach()
        x_enc = x_enc - means
        x_enc = x_enc.masked_fill(mask == 0, 0)
        stdev = torch.sqrt(torch.sum(x_enc * x_enc, dim=1) /
                           torch.sum(mask == 1, dim=1) + 1e-5)
        stdev = stdev.unsqueeze(1).detach()
        x_enc /= stdev
 
        # embedding
        enc_out = self.enc_embedding(x_enc, x_mark_enc)  # [B,T,C]
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))
        # porject back
        dec_out = self.projection(enc_out)
 
        # De-Normalization from Non-stationary Transformer
        dec_out = dec_out * \
                  (stdev[:, 0, :].unsqueeze(1).repeat(
                      1, self.pred_len + self.seq_len, 1))
        dec_out = dec_out + \
                  (means[:, 0, :].unsqueeze(1).repeat(
                      1, self.pred_len + self.seq_len, 1))
        return dec_out
 
    def anomaly_detection(self, x_enc):
        # Normalization from Non-stationary Transformer
        means = x_enc.mean(1, keepdim=True).detach()
        x_enc = x_enc - means
        stdev = torch.sqrt(
            torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
        x_enc /= stdev
 
        # embedding
        enc_out = self.enc_embedding(x_enc, None)  # [B,T,C]
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))
        # porject back
        dec_out = self.projection(enc_out)
 
        # De-Normalization from Non-stationary Transformer
        dec_out = dec_out * \
                  (stdev[:, 0, :].unsqueeze(1).repeat(
                      1, self.pred_len + self.seq_len, 1))
        dec_out = dec_out + \
                  (means[:, 0, :].unsqueeze(1).repeat(
                      1, self.pred_len + self.seq_len, 1))
        return dec_out
 
    def classification(self, x_enc, x_mark_enc):
        # embedding
        enc_out = self.enc_embedding(x_enc, None)  # [B,T,C]
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))
 
        # Output
        # the output transformer encoder/decoder embeddings don't include non-linearity
        output = self.act(enc_out)
        output = self.dropout(output)
        # zero-out padding embeddings
        output = output * x_mark_enc.unsqueeze(-1)
        # (batch_size, seq_length * d_model)
        output = output.reshape(output.shape[0], -1)
        output = self.projection(output)  # (batch_size, num_classes)
        return output
 
    def forward(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask=None):
        if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
            dec_out = self.forecast(x_enc, x_mark_enc, x_dec, x_mark_dec)
            return dec_out[:, -self.pred_len:, :]  # [B, L, D]
        if self.task_name == 'imputation':
            dec_out = self.imputation(
                x_enc, x_mark_enc, x_dec, x_mark_dec, mask)
            return dec_out  # [B, L, D]
        if self.task_name == 'anomaly_detection':
            dec_out = self.anomaly_detection(x_enc)
            return dec_out  # [B, L, D]
        if self.task_name == 'classification':
            dec_out = self.classification(x_enc, x_mark_enc)
            return dec_out  # [B, N]
        return None

这位同学解读的代码也可以 

(291条消息) TimesNet 代码阅读_刘泓君的博客-CSDN博客

参考资料

（2023 ICLR）TimesNet：Temporal 2D-Variation Modeling for General Time Series Analysis - 知乎 (zhihu.com)

ICLR 2023 ｜任务通用的时序分析骨干网络TimesNet - 知乎 (zhihu.com)