DAY37：贪心算法（四）跳跃游戏+跳跃游戏Ⅱ_[算法课贪心] 跳跃游戏

55.跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
1
2
3

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
1
2
3

提示：

• 1 <= nums.length <= 3 * 104
• 0 <= nums[i] <= 105

思路

游戏大致规则如下图。每一步代表着能跳跃的最大长度。能通过不同的步数组合，跳到最后一个下标就输出true。

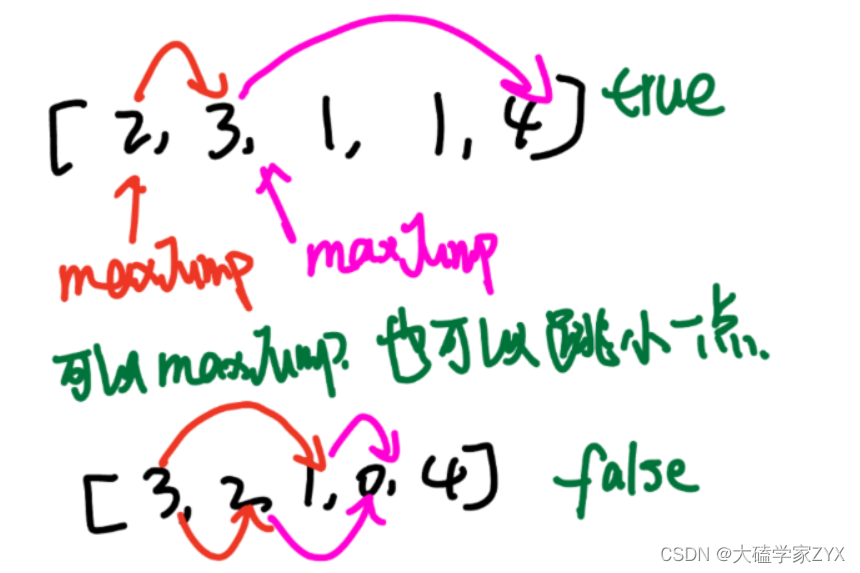
本题直接看每个元素应该跳几步很难解出来，需要去看覆盖范围。如下图所示。

也就是说，不要管跳几步，不看具体是怎么跳的，只看每个数字的覆盖范围。如果是3，就覆盖后面三个数，如果是2，就覆盖后面两个数。

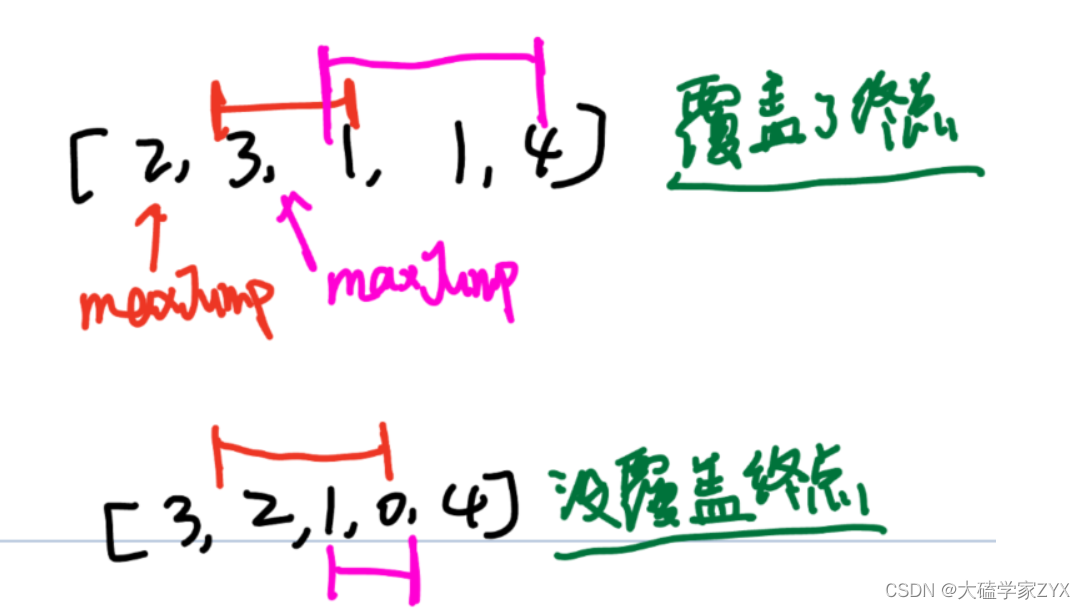
完整版

• 在已有的覆盖范围内遍历每一个元素，得到新的可跳跃的步数，增加覆盖范围，取最大的覆盖范围

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover=0;
        if(nums.size()==1) return true;
        //此时是i<=cover而不是i<=nums.size()，因为是在覆盖范围内部遍历
        for(int i=0;i<=cover;i++){
            //找范围内最大的cover数值
            cover = max(i+nums[i],cover);
            if(cover>=nums.size()-1){
                return true;
            }
        }
        //如果遍历完了cover还没找到
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

这种思路还是比较难以理解的话，可以看下面的图进行对比。

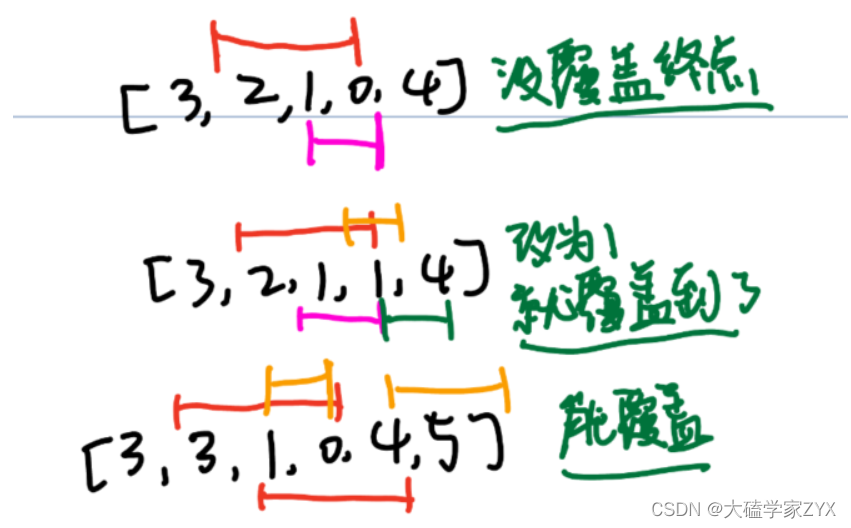
由上图可知，我们不需要知道他的跳跃路径，只需要看cover内部，最大的覆盖范围就行了！

总结

这道题目关键点在于：不用拘泥于每次究竟跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的。

从这道题也可以看出来贪心并没有什么套路，只能多接触，没接触的话想不出来，接触之后下次就要考虑这种思维。

45.跳跃游戏Ⅱ

视频课程：贪心算法，最少跳几步还得看覆盖范围 | LeetCode： 45.跳跃游戏II_哔哩哔哩_bilibili

• 本题解法也不太好想，最好结合视频课程和画图一起理解。

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
1
2
3
4

示例2：

输入: nums = [2,3,0,1,4]
输出: 2
1
2

提示:

• 1 <= nums.length <= 104
• 0 <= nums[i] <= 1000
• 题目保证可以到达 nums[n-1]

思路

本题和跳跃游戏的区别是，本题需要输出最少跳几步，才能跳到终点的位置。

此时也不能每一步都跳最大值，因为最少的情况并不一定是每一步都跳了当前的最大值。

本题依然是用覆盖范围的思想，每跳一步，尽可能地增加覆盖范围。只要覆盖范围覆盖了终点，说明用当前步数就可以跳到终点位置。

完整版

• 本题的条件，也是i<=cover,没必要用i<=nums.size()
• 但是本题多了一步next，也就是下一步的值，是记录cover内部遍历过的下一步的最大值
• 注意next是记录的下一步能达到的最大的下标结果值，包括了数值很大但是本身很靠前的情况。

class Solution {
public:
    int jump(vector<int>& nums) {
        //如果数组长度只有1，那么就是0步
        if(nums.size()==1) return 0;
        int cover=0;
        //统计下一步的覆盖范围，是cover内的最大值
        int next=0;
        int result=0;
        //本题的条件，也是i<=cover,没必要用i<=nums.size()
        for(int i=0;i<=cover;i++){
            next=max(i+nums[i],next);//只记录遍历过的数字里，最大的下一步的下标值
            if(i==cover){//移动到了当前的终点
                if(i<nums.size()-1){//如果没到头，就再走一步
                    result++;
                    cover=next;//启动下一步覆盖范围，一旦覆盖到终点，立即break，因为result已经++了
                    if(cover>=nums.size()-1){
                    	break;
                    }
                }
                //如果到头了,也就是当前的cover已经到终点了
                else
                    break;
            }
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

为什么next覆盖到了终点可以直接break，不用加上最后一步

本题的逻辑是，当达到cover的时候，result直接跳出循环。

例如输入[2,3,1,1,4]，cover的时候遍历到nums[2]的时候，加上next已经满足条件，直接break出去，并没有对result再次进行++操作。

这是因为最开始的时候cover=0，而i也=0，也就是说最开始的时候已经累积一步了！由于我们把长度为1只有一个数字的情况单独放了，所以遍历到下面一定是长度>=2的，至少要走一步。相当于最开始已经累积一步了。

逻辑梳理

在这个算法中，每一次跳跃实际上都是在覆盖范围（cover）的边界上进行的，而不是在覆盖范围内部。

所以当我们第一次进入循环时，i等于cover（都是0），并且这时我们实际上已经做了第一次“跳跃”，也就是从起点跳到了能够覆盖的最远距离，因此result增加1。然后，每一次当i再次等于cover时，我们就会进行下一次跳跃，也就是从当前覆盖范围的边界跳到下一次能够到达的最远位置（也就是max(i+nums[i]）。

当遍历到cover的时候，如果cover已经覆盖到了数组的末尾，那么我们就直接跳出循环，因为这表示我们已经跳到了终点，没有必要再跳了。但是在跳出循环之前，我们已经把这次跳跃计入了result中，所以不会漏掉最后一次跳跃。

总结

这道题比起跳跃游戏Ⅰ难了很多，本题关键在于，以最小的步数增加最大的覆盖范围，直到覆盖范围覆盖了终点，这个范围内最小步数一定可以跳到，不用管具体是怎么跳的，也不用纠结于一步究竟跳一个单位还是两个单位。

这也是一个贪心策略，我们试图在每次跳跃中到达能覆盖更远的位置。所以在每一轮循环中，我们尝试遍历当前的覆盖范围（cover）内的所有位置，并在这个范围内找到能够跳跃到的最远位置的下标，这个最远的距离我们保存在变量next中，将next与最后一个下标对比。

当数组长度大于1时，我们实际上是在循环开始时就已经“预先”计算了一次跳跃，所以当next超出范围，直接break，不会漏掉任何一次跳跃。