当前位置: article > 正文

了解语言模型Model Language，NLP必备

作者：繁依Fanyi0 | 2024-05-02 22:16:24

踩

语言模型

语言模型是预测接下来出现什么词的任务。理论上说，您还可以将语言模型视为为一段文本分配概率的系统。

实践上说，您每天都在使用语言模型。当你在网页搜索上输入的文字时，当你输入今天，手机就会自动计算概率分布，并且弹出是什么日子，是农历几月几日单词等等供你选择。

还有你的输入法也会根据目前你输入的字计算概率，有多个选择供你选。

1. 统计语言模型

统计语言模型(Statistical Language Model)是所有 NLP 的基础。在语音识别系统中,对于给定的语音段 Voice,需要找到一个使概率 p(Text|Voice)最大的文本段 Text，利用 Bayes 公式，有:

$p(Text|Voice) = \frac {p(Voice|Text)p(Text)} {p(Voice) }$

p(Voice|Text)为声学模型，p(Voice|Text)为语言模型。

统计语言模型是用来计算一个句子的概率的概率模型。假设 $W = w_1^T$ = $w_1, w_2, \ldots, w_T$ ，示由 T 个词 $w_1, w_2, \ldots, w_T$ 按顺序构成的一个句子,则 $w_1, w_2, \ldots, w_T$ 的联合概率为:

$p(W) =P(w_1^T)=$ $P(w_1, w_2, \ldots, w_T)$

就是这个句子的概率。利用 Bayes 公式，上式可以被链式地分解为:

$P(W)=P(w_1^T) = P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1^2) \cdots P(w_T \mid w_1^{T-1})$

其中的(条件)概率 $P(w_1), P(w_2 \mid w_1) ,P(w_3 \mid w_1^2) ,\cdots, P(w_T \mid w_1^{T-1})$ 就是语言模型的参数。

参数 $P(w_k \mid w_1^{k-1})(k>1)$ 的近似计算，利用 Bayes 公式，有:

$P(w_k \mid w_1^{k-1})= \frac {P(w_1^k )}{ P(w_1^{k-1}) }\approx \frac {count(w_1^k )}{count (w_1^{k-1})}$

其中 ${count(w_1^k )}$ 和 ${count(w_1^{k-1 })}$ 分别为单词 $w_1^{k }$ 和 $w_1^{k-1 }$ 在语料中出现的次数。

2. n-gram 模型

模型的基本思想：基于Markov,一个词出现的概率只与它前面n-1个词相关，即：

$P(w_k \mid w_1^{k-1}) \approx P(w_k \mid w_{k-n+1}^{k-1}) \approx \frac {count(w_{k-n+1}^{k} )}{count (w_{k-n+1}^{k-1})}$

这一简化不仅使单个参数的统计变得更容易(统计时需要匹配的词串更短)，也使参数的总数变少了。

模型参数的量级是 N 的指数函数 $O(N^n)$ ，显然 n 不能取得太大，实用中最多的是采用 n=3 的三元模型。从理论上看，n 越大效果越好。但是，当 n 大到一定程度时，模型效果的提升幅度会变小。例如，当 n 从 1 到 2，再从 2 到 3 时，模型的效果上升显著，而从 3 到 4 时，效果的提升就不显著了。参数越多，可区别性越好，但同时单个参数的实例变少从而降低了可靠性，因此需要在可靠性和可区别性之间进行折中。

例如，我们学习一个4-gram语言模型：

假设在语料库中“students opened their”发生了 1000 次，

若:“students opened their books”发生了 400 次，则:P(books | students opened their) = 0.4;

若:“students opened their exams”发生了 100 次，则:P(exams | students opened their)= 0.1;

但是

若在语料库中“students opened their w ”从未出现在数据中怎么办？也就是 $count (w_{k-n+1}^{k}) = 0$ ，就认为 $P(w_k \mid w_1^{k-1})$ 概率为零吗？
若“students opened their”未出现在数据中那有怎么办？也就是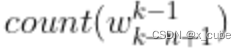=0。
若在语料库中“students opened their w ”出现的次数和和“students opened their”出现的次数相同，也就是 $count (w_{k-n+1}^{k}) = count (w_{k-n+1}^{k-1})$ ，那么能否认为 $P(w_k \mid w_1^{k-1})$ 就等于 1 呢?

那么，在这种情况下，我们应该丢弃“proctor”的上下文(图中划红线部分)吗? 这就引出了 n-gram 语言模型的两个主要问题:稀疏性和存储。

2.1 n-gram语言模型的稀疏性问题

些模型的稀疏性问题是由两个情况引起的

2.2 n-gram 语言模型的存储问题

我们知道需要存储在语料库中看到的所有 n-gram 的统计数。随着 n 的增加(或语料库大小的增加)，模型的大小也会增加。

3. 基于窗口的神经语言模型

在机器学习中有一种通用模型:对所考虑的问题建模后，首先为其构造一个目标函数，其次对这个目标函数进行优化，然后求得一组最优的参数，最后利用这组最优参数对应的模型来进行预测。

$L = \sum_{w\in C} log p(w|Context (w)) (3.1)$

由此可见，概率 $p(w|Context (w)$ 已被视为关于w和context(w)的函数：

$p(w\mid Context (w)) = F(w, Context (w), \theta )(3.2)$

其中:θ为待定参数集。因此，一旦对公式3.1进行优化得到最优参数集θ*后，F 也就唯一被确定了，以后任何概率 p(w|Context(w))就可以通过函数 F(w，Context(w)，θ)来计算了。

下面介绍一种通过神经网络来构造 F 的方法，即 Bengio《A neural probabilistic language model. Journal of Machine Learning Research》(2003)的神经概率语言模型。其中首次解决了上面所说的“维度灾难”，这篇论文提出一个自然语言处理的大规模的深度学习模型，这个模型能够通过学习单词的分布式表示，以及用这些表示来表示单词的概率函数。图3.1 给出了该模型的示意图，它包括四个层: 输入(Input)层、投影(Projection)层、隐藏(Hidden)层和输出(Output)层。

图3.1：首个 NLP 神经网络架构模型(Bengio 模型) 图3.2:对 Bengio 模型的简化表示

这个模型的简化版本如图3.2所示，其中蓝色的层表示输入单词的embedding拼接:e=[e(1);e(2);e(3);e(4)]，红色的层表示隐藏层: $h=f(We+b_1)$ ，绿色的输出分布是对词表的一个 softmax 概率分布: $y = softmax(Uh+b_2)$

例如构建一个基于固定窗口的神经语言模型。首先，了解一下固定窗口的案例，见图:

然后，建立一个固定窗口神经语言模型,如图：

Bengio 模型对 n-gram LM 的改进:

没有稀疏问题。
没有存储问题:不需要存储所有观察到的 n-gram。

遗留问题:

固定窗口太小
放大窗口放大 W
窗口永远不够大!
x(1) 和 x(2) 乘以 W 中完全不同的权重。输入的处理方式不对称。

因此，我们需要一个可以处理任何长度输入的神经架构。

4. 语言模型的评估指标:困惑度

其中分母项（ $P_{LM}$ ）是指在语言模型在语料库中的逆概率。指数项（1/T）是指用单词数量做归一化。最后的式子中，表示困惑度等于交叉熵损失J(θ)的指数。

语言模型的困惑度越低越好！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/526355