利用matlab实现POD分解(在一维信号或二维流场矢量中的应用）

（2020年7月更新，增加POD算法中svd函数的’econ‘’选项，目的是加快svd方法的计算速度。）
（2020年7月更新2，增加前言相关的正交性的简单说明）
（2020年8月更新，在程序中对旧版本矩阵与向量.*不兼容进行注释）
（2021年3月更新，更改一些细节，感谢VTgrm大佬的评论建议）

0 前言

POD是一种常用的数据降维方法，全程为Proper orthogonal decomposition，翻译为中文叫做本征正交分解。本文主要是尝试利用matlab对POD方法进行实现。
本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。
由于POD可能涉及到了包括且不限于流体、机械、信号、控制、深度学习等各领域，所以请各位大佬们如果发现错误，或者有什么补充，欢迎在评论区指出，感谢。

如果想看有关DMD分解文章，可以点击下面链接
【利用matlab实现DMD分解(在一维信号或二维流场矢量中的应用）】

文章里用到的参考列出在下面：
[1]一文让你通俗理解奇异值分解
https://www.jianshu.com/p/bcd196497d94
[2]有限长平板分离再附流动非定常特性的 PIV 实验研究（张青山）
[3]Modal Analysis of Fluid Flows: An Overview（Kunihiko Taira、Steven L. Brunton等人）

0.1 matlab中特征值计算

matlab中特征值和特征向量都可以用eig()函数进行计算。

[V,D] = eig(A)
1

其中V为特征向量组成的矩阵，D为特征根所组成的矩阵。A、V和D三个矩阵之间的关系为：A* V = V* D。
其中V的每一列都为一个特征向量，特征值对应的D矩阵中对角线上的相应列。

在矩阵乘法中，特征向量可以表示为变化的方向，特征根表示为变化的大小。如下图所示，矩阵A=[0.95,-0.35;-0.35,0.95]，其特征值为0.6和1.3，特征向量的方向一个为45度，一个-45°。矩阵A对于随机点阵的效果如下所示。可以看到在经过矩阵A相乘后，随机点阵发生了变形，变形的方向就是特征向量的方向，变形的大小就是特征根的大小。大于1的方向拉长，小于1的方向缩短。

0.2 matlab中SVD分解计算

SVD是一种常用的数据压缩算法，可以将一个较大的矩阵压缩为几个小矩阵相乘的形式。当然我这么说不直观，接下来先用示例解释一下。

matlab中有自带的svd函数，svd计算分解如下：

[U,S,V] = svd(A)
1

其中A = U * S * V '。

这时有人会质疑，哪里数据压缩了，原来的A矩阵变成了3个，明显数据量增大了呀。这时就体现出SVD的奇异值分解的作用了。SVD中的S矩阵为奇异值矩阵，也是一个对角矩阵，对角线上分布着奇异值，由大到小进行排列。奇异值越大，对矩阵的贡献越大，所以根据这个原理，我们可以删除掉一些小的奇异值，只保留大的奇异值，也可以让矩阵近似成立。

比如上图，我们只保留了前3个最大的奇异值，并将其余不参与计算的矩阵删除（用灰色表示）。如果后面的舍弃的奇异值很小，则计算出的结果与原来的A矩阵会十分接近。

接下来用一个例子来解释：

%SVD的实验
%演示SVD数据的压缩
Z = peaks(100);
[U,S,V] = svd(Z);%SVD分解

K=1;%前1个奇异值
U1=U(:,1:K);S1=S(1:K,1:K);V1=V(:,1:K);
Z1=U1*S1*V1';

K=2;%前2个奇异值
U2=U(:,1:K);S2=S(1:K,1:K);V2=V(:,1:K);
Z2=U2*S2*V2';

K=5;%前5个奇异值
U5=U(:,1:K);S5=S(1:K,1:K);V5=V(:,1:K);
Z5=U5*S5*V5';

figure(1);colormap(jet);
subplot(2,2,1)
pcolor(Z);shading interp;axis off
subplot(2,2,2)
pcolor(Z1);shading interp;axis off
subplot(2,2,3)
pcolor(Z2);shading interp;axis off
subplot(2,2,4)
pcolor(Z5);shading interp;axis off
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

我们看到，虽然原矩阵总共有100个奇异值，但是当我们只取到前5个奇异值时，新矩阵和原来的矩阵就之间已经看不出任何差别。之后的95个奇异值的舍弃几乎不损失任何信息，我们只保存前5个奇异值和相应的矩阵U*、V*即可。

之后也简单介绍一下SVD和特征值之间的关系。
当矩阵A可以分解为下面的形式
$$A=U\cdot S\cdot V^T$$
则矩阵V可以计算为：
$$\left(A^{T}A\right)\cdot V=D\cdot V$$
上面两式的V是相同的。
特征值和奇异值之间也存在关系，上式的特征值D开根号就等于奇异值S。
$${\sqrt{D}}_i=S_i$$

知道SVD一些基本知识后，会有助于之后POD方法的理解。

0.3 信号的正交性

POD叫做本征正交分解，分解出的信号都是正交的。
正交在几何上可以描述为，向量互相的垂直，或者可以说是一个向量在另一个向量上的投影为0。

对于信号之间的正交，我们定义当两个信号x和y的内积为0时，则正交：
$$\int x\left(t\right)y\left(t\right)dt=0$$

说完了正交，我们再提一下分解。信号的分解可以理解为，我们把信号分解为很多信号叠加的形式。比如下面公式中，把信号x分解为很多${\phi }_i$叠加的形式。
$$x\left(t\right)=\sum a_i\cdot {\phi }_i\left(t\right)$$
我们把${\phi }_i$称为基，将很多‘基’作为元素乘以常系数a，再进行叠加，我们就可以还原得到信号x。

如果改变常系数$a_i$，我们则可以得到不同的信号x，这些不同的信号x组成的一个集合，定义为空间X。通过类比几何坐标系的坐标表示方式，‘基’可以看做空间X中的坐标轴，常数$a_i$可以视为坐标值。（其实POD分解就相当于给出了一种空间X的表示方式，这个学完POD之后可以对比一下）

如果我们分解得到的基之间可以两两正交，我们就称这个分解是正交分解。最常见的正交分解就是傅里叶分解，得到的正弦函数之间互相正交。

比如以下面的信号为例：

构建了一个Perlin噪声，并进行正交分解，得到3个正交基${\phi }_1,{\phi }_2,{\phi }_3$。这三个正交基可以通过下面的方式得到原信号。
$$x=-0.954{\phi }_1+0.006{\phi }_2-0.677{\phi }_3$$

正交分解有以下的特点：
1.正交性
< φ i , φ j > = { 1      ( i = j ) 0      ( i ≠ j ) \left< \varphi _i,\varphi _j \right> =\left\{

$$\begin{array}{l} 1\ \ \ \ \left( i=j \right)\\ 0\ \ \ \ \left( i\ne j \right)\\ \end{array}$$ \right. ⟨φi​,φj​⟩={1    (i=j)0    (i=j)​
自身的内积等于1，和其它正交基的内积等于0。这个性质在matlab里可以利用sum(PhiU_1 .* PhiU_2)来验证。
2 信号的能量分解前后不变（Parseval定理）
由于基是正交的，所以分解后正交基本身的能量等于1，每一个模态的能量就等于系数a的平方。所以对于POD分解，每一帧时间步i，都有

sum((U_tx(i,:)-U0x).^2) - sum(An(1,:).^2) = 0
1

这个可以在之后POD程序里进行验证。

3 最小平方近似性质
已知信号可以被分解为如下的形式
$$x\left(t\right)=\sum _{i=1}^n{a}_n{\phi }_n\left(t\right)$$
如果我们取前L个基（L<n），作为信号x的近似，则定义这个近似信号为y
$$y\left(t\right)=\sum _{i=1}^L{b}_n{\phi }_n\left(t\right)$$
定义最小平方近似，来描述两个信号的相似度。
$$D=sum((x-y{)}^2)$$
我们希望两个信号尽可能近似，也就是令两个信号差的平方和D最小。那么，只需要令bn=an即可。也就是说，分解得到的an不需要改动，天然的就满足于最佳近似。（POD分解中，删除掉小能量模态，得到的结果也是最佳近似的）

1 一维信号POD分解

1.1 原始的POD分解

对于随时间变化的一维信号，由于添加了时间维，所以记录在一个二维矩阵Utx内。信号的空间长度为m的离散点，时间长度为N个离散点。二维矩阵具有N行m列，每一行都代表信号在某一个时间点上的形状。
U t x = [ u ( t 1 , x 1 ) u ( t 1 , x 2 ) ⋯ u ( t 1 , x m ) u ( t 2 , x 1 ) u ( t 2 , x 2 ) ⋯ u ( t 2 , x m ) ⋮ ⋮ ⋱ ⋮ u ( t N , x 1 ) u ( t N , x 2 ) ⋯ u ( t N , x m ) ] U_{tx}=\left[

$$\begin{matrix} u\left( t_1,x_1 \right)& u\left( t_1,x_2 \right)& \cdots& u\left( t_1,x_m \right)\\ u\left( t_2,x_1 \right)& u\left( t_2,x_2 \right)& \cdots& u\left( t_2,x_m \right)\\ \vdots& \vdots& \ddots& \vdots\\ u\left( t_N,x_1 \right)& u\left( t_N,x_2 \right)& \cdots& u\left( t_N,x_m \right)\\ \end{matrix}$$ \right] Utx​= ​u(t1​,x1​)u(t2​,x1​)⋮u(tN​,x1​)​u(t1​,x2​)u(t2​,x2​)⋮u(tN​,x2​)​⋯⋯⋱⋯​u(t1​,xm​)u(t2​,xm​)⋮u(tN​,xm​)​ ​

原始的POD分解步骤如下：

首先建立协方差矩阵R
$$R=1/N\cdot \left(U_{tx}^{\prime }\cdot U_{tx}\right)$$
之后进行特征值和特征向量分解，V是特征向量，D是特征根：
$$R\cdot V=D\cdot V$$
特征向量就是我们得到的POD模态，特征根对应的每个模态的能量值，同样我们关注大的特征根对应的模态。一般把最大的特征根对应的模态称为第一模态。
V = [ ϕ 1 ϕ 2 ⋯ ϕ m ] V=\left[

$$\begin{matrix} \phi _1& \phi _2& \cdots& \phi _m\\ \end{matrix}$$ \right] V=[ϕ1​​ϕ2​​⋯​ϕm​​]
模态的幅值和大小可以用A表示
$$A=U\cdot V$$
每一个模态对应的时间变化为
$$A_i=U\cdot {\varphi }_i$$
这样，我们成功的将一个时间和空间信号，拆分成两个独立的时间信号和空间信号的乘积，每一个i代表一个模态。
$$U\left(t,x\right)=\sum _{i=1}^m{A}_i\left(t\right)\cdot {\varphi }_i\left(x\right)$$
一般前几个模态的能量（特征根）往往远大于后面的能量，所以也就是说模态只需要分析前几个就足以概括整个信号特点。

一般的信号往往还具有一个平均值，做POD分解前，需要先把平均信号分量去掉。

接下来对应的matlab代码如下：

%POD

clear
close all
%0初始化
x=0:0.02:10;
t=0:0.02:5-0.02;
Fs=1/(t(2)-t(1));
[X,T]=meshgrid(x,t);
%1构建信号
q=1.6*sin(2*pi*(X+2*T))+0.5*sin(2*pi*(3*X+4*T))+0.1;
N=size(T,1);%时间长度
m=size(X,2);%空间长度

%POD分解

[U0x,An,PhiU,Ds]=POD_CLASS(q);%原始POD（在N远大于m时用可以加快速度节省内存）

%[U0x,An,PhiU,Ds]=POD_SNAP(q);%快照POD（在N远小于m时用可以加快速度节省内存）
%[U0x,An,PhiU,Ds]=POD_SVD(q);%基于SVD分解的POD

%POD演示
SHOW_POD_1(U0x,An,PhiU,Ds,x,t,q);%动态演示模态叠加的效果

SHOW_POD_2(U0x,PhiU,Ds,x);%前3阶模态分析

SHOW_POD_3(An,PhiU,Ds,x,t,3);%对单独模态进行时间序列分析(以第3模态为例）





function [U0x,An,PhiU,Ds]=POD_CLASS(Utx)
%原始经典POD
%输入Utx，其中时间离散长度N=size(Utx,1)，空间离散长度m=size(Utx,2)
%输出U0x，0阶模态，可以看做定常平均值
%输出An：时间变量，对应模态的幅值随时间的变化，可以用来做时间序列分析
%输出phiU：POD的模态
%输出Ds：特征值Ds反映了每一个模态对应的能量，可以用来排序
N=size(Utx,1);%时间
m=size(Utx,2);%空间

%0阶
U0x=mean(Utx,1);%空间平均
Utx=Utx-U0x.*ones(N,m);%低版本Matlab用Utx=Utx-(ones(N,1)*U0x).*ones(N,m); 代替
%利用特征值和向量的方式，进行POD分解
R=1/N*(Utx'*Utx);
[PhiU,D] = eig(R);%phiU是基函数，也是POD模态
An=Utx*PhiU;
%排序
Ds=diag(D);
[~,ind]=sort(Ds,'descend');
Ds = Ds(ind);
An=An(:,ind);
PhiU=PhiU(:,ind);
end

function SHOW_POD_1(U0x,An,PhiU,Ds,x,t,Utx)
%动态显示
figure()
N=length(t);
Limit_Y=[-2,2];

for k=1:100
clf
subplot(3,2,1)%原始
plot(x,Utx(k,:))
ylim(Limit_Y)
title('原始数据')

subplot(3,2,3)%平均
plot(x,U0x)
ylim(Limit_Y)
title('平均数据')

subplot(3,2,4)%1阶加2阶
P1=An(k,1).*PhiU(:,1)';
P2=An(k,2).*PhiU(:,2)';
plot(x,U0x+P1+P2)
ylim(Limit_Y)
title('0阶至2阶模态总和')

subplot(3,2,5)%1至4阶
P3=An(k,3).*PhiU(:,3)';
P4=An(k,4).*PhiU(:,4)';
plot(x,U0x+P1+P2+P3+P4)
ylim(Limit_Y)
title('0阶至4阶模态总和')

subplot(3,2,6)%1至6阶
P5=An(k,5).*PhiU(:,5)';
P6=An(k,6).*PhiU(:,6)';
plot(x,U0x+P1+P2+P3+P4+P5+P6)
ylim(Limit_Y)
title('0阶至6阶模态总和')


subplot('Position',[0.65,0.7,0.2,0.2])
N_En=2;
En=[Ds(1:N_En);sum(Ds)-sum(Ds(1:N_En))];
pie(En,[ones(1,N_En),1]) 
title('1阶与2阶模态能量占比','Position',[0,1.6,0])

pause(0.1)
end
end

function SHOW_POD_2(U0x,PhiU,Ds,x)
Limit_Y=[-2,2];
figure()
%4个模态图
subplot('Position',[0.08,0.79,0.45,0.16])%平均0阶
plot(x,U0x)
ylim(Limit_Y)
title('0阶模态/平均值')

subplot('Position',[0.08,0.54,0.45,0.16])%1阶模态
plot(x,PhiU(:,1))
title('1阶模态')

subplot('Position',[0.08,0.30,0.45,0.16])%2阶模态
plot(x,PhiU(:,2))
title('2阶模态')

subplot('Position',[0.08,0.05,0.45,0.16])%3阶模态
plot(x,PhiU(:,3))
title('3阶模态')

%能量分布
Ds_N=Ds/sum(Ds);
Cum_Ds_N=cumsum(Ds_N);
%N_Cum_95=sum((Cum_Ds_N<0.95));
N_Cum_95=10;
subplot('Position',[0.6,0.79,0.3,0.17])%总的能量分布
bar( 1:N_Cum_95 , Cum_Ds_N(1:N_Cum_95) ,'BarWidth',1)
ylim([0,1]);

subplot('Position',[0.65,0.54,0.3,0.17])%1阶模态能量占比
pie([Ds_N(1),1-Ds_N(1)],{[num2str(100*Ds_N(1),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])

subplot('Position',[0.65,0.30,0.3,0.17])%2阶模态能量占比
pie([Ds_N(2),1-Ds_N(2)],{[num2str(100*Ds_N(2),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])

subplot('Position',[0.65,0.05,0.3,0.17])%3阶模态能量占比
pie([Ds_N(3),1-Ds_N(3)],{[num2str(100*Ds_N(3),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])
end

function SHOW_POD_3(An,PhiU,Ds,x,t,Mode)
figure()
%对单独模态进行时间序列分析
subplot('Position',[0.08,0.58,0.5,0.35])%模态显示
plot(x,PhiU(:,Mode))
title([num2str(Mode),'阶模态'])

subplot('Position',[0.08,0.10,0.5,0.35])%功率谱分析
Fs=1/(t(2)-t(1));
N=length(t);
[pxx,f]=pwelch(An(:,Mode),N-1,round(N/2),t,Fs);
plot(f,pxx)%功率谱
title([num2str(Mode),'阶模态时间功率谱'])

subplot('Position',[0.58,0.14,0.4,0.3])%能量占比
Ds_N=Ds/sum(Ds);
pie([Ds_N(Mode),1-Ds_N(Mode)],{[num2str(100*Ds_N(Mode),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])
title(['能量占比'],'Position',[0,1.6,0])

text(0.2,4.0,{'POD分解',['第',num2str(Mode),'阶模态分析']},'FontSize',22,'HorizontalAlignment','center')

end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173

信号q的表达式为
$$q=1.6\ast \sin (2\pi (X+2T))+0.5\sin (2\pi (3X+4T))+0.1;$$
其中包含3项，一个常数项0.1。一个空间频率1hz时间频率2hz的正弦波，和一个空间频率3hz时间频率4hz的正弦波。接下来我们看看POD是怎样把这些信号分离出来。

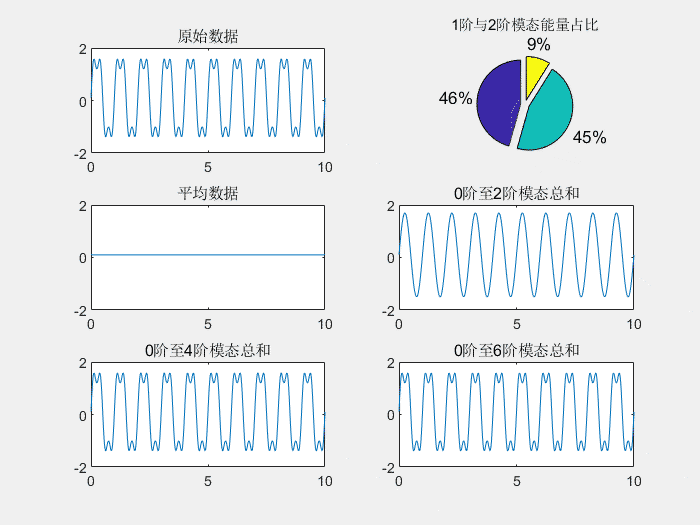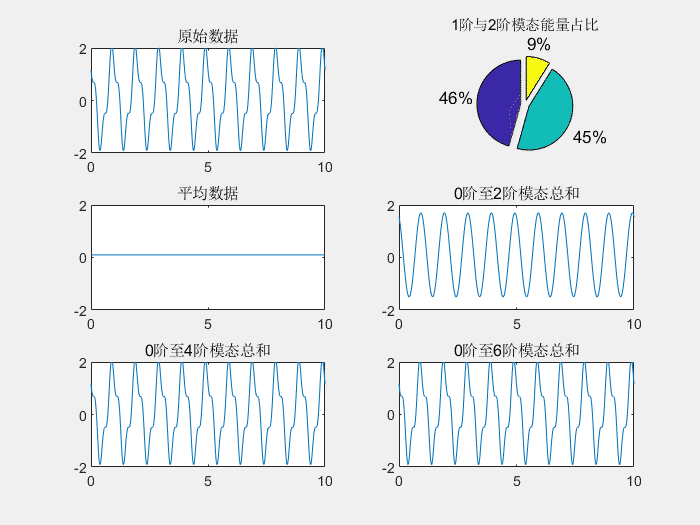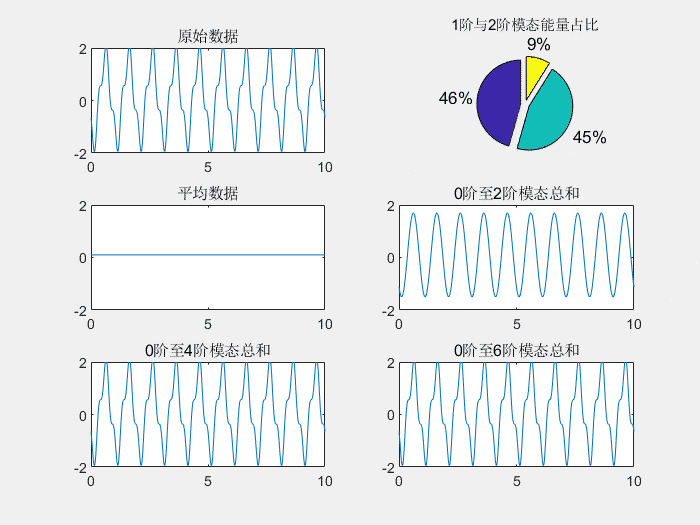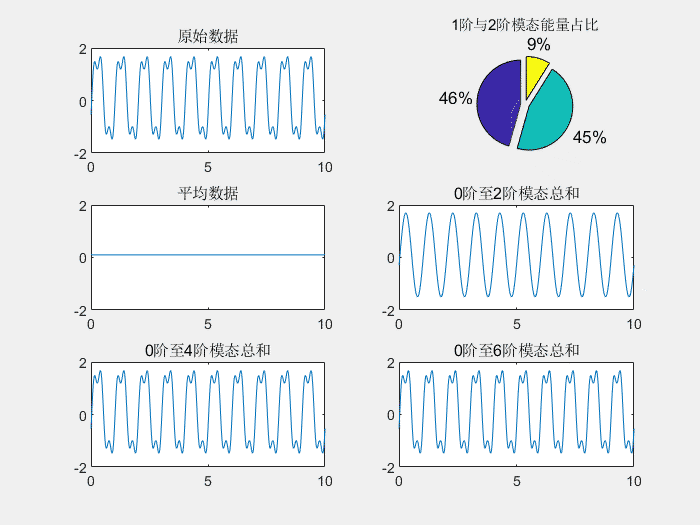
上图为POD分解的示意图，前4阶模态的和就和原信号几乎完全相同，而前2阶模态的能量占比分别为46%和45%，几乎占据了全部能量。如果第一模态能量能够占30%以上，而且模态能量占比快速递减，就说明结果还是不错的。

上图展示了不同的模态形状和模态所占的能量。其中1阶模态和2阶模态的频率为1hz，这符合空间频率为1hz的正弦分量。3阶模态和4阶模态的频率为3hz，也符合之前空间频率3hz的正弦分量。

其中1阶和2阶模态空间频率相同，构成一对模态，来描述时间上的运动。具体数学上的分解可以用简单的三角函数分解计算得到：
$$\sin (2\pi (X+2T))=\sin (2\pi X)\cos (2\pi \cdot 2T)+\cos (2\pi X)\sin (2\pi \cdot 2T)$$
其中带X的项为模态，带T的项为时间变化。同理，第3和第4模态也可以构成一对。因此，如果在POD分解中看到这样一对的模态出现，则意味着实际信号中一个移动的正弦波。

单独提取出第3模态进行分析：

对时间An做功率谱分析，还可以得到模态的时间序列的分析。比如3模态的时间功率谱，就对应着时间频率为4hz的正弦分量。

所以总的说，特征根代表能量，决定模态的排序和能量占比；特征向量V代表着模态，决定着空间信息；幅值A代表着模态随时间变化的幅值，决定着时间信息。

1.2 快照POD分解（Snapshot-POD）

快照POD（Snapshot-POD）的出现主要来自于实际的数据中，一般空间离散点要远远大于时间离散点，也就是矩阵Utx中，m远大于N。这时就会出现一个问题：
$$R=1/N\cdot \left(U_{tx}^{\prime }\cdot U_{tx}\right)$$
在这个步骤中，R是一个m行m列的矩阵。如果m非常大，则电脑无论是储存，还是在后面计算特征向量等步骤，都会非常困难。所以针对这个问题，有一个间接的办法也可以计算出POD：
$$C=\left(U_{tx}\cdot U_{tx}^{\prime }\right)$$
这样C就是一个N行N列的矩阵，计算起来要简单的多。
之后是快照POD的步骤，首先还是一样，进行特征值和特征向量的分解：
$$C\cdot Au=D\cdot Au$$
这里D是特征根矩阵。
之后模态矩阵V可以计算得到：
$$V=U_{xt}\cdot Au/\sqrt{D}$$
幅值An也可以计算得到：
$$An=U_{tx}\cdot V$$
这里的Utx是Uxt的转置矩阵，相当于交换了时间维和空间维。

matlab程序以及演示如下：

%POD

clear
close all
%0初始化
x=0:0.02:10;
t=0:0.02:5-0.02;
Fs=1/(t(2)-t(1));
[X,T]=meshgrid(x,t);
%1构建信号
q=1.6*sin(2*pi*(X+2*T))+0.5*sin(2*pi*(3*X+4*T))+0.1;
N=size(T,1);%时间长度
m=size(X,2);%空间长度
%POD分解
[U0x,An,PhiU,Ds]=POD_SNAP(q);%快照POD（在N远小于m时用可以加快速度节省内存）
%POD演示
SHOW_POD_2(U0x,PhiU,Ds,x);%前3阶模态分析



function [U0x,An,phiU,Ds]=POD_SNAP(Utx)
%快照POD，输入输出与原始POD相同
%输入Utx，其中时间离散长度N=size(Utx,1)，空间离散长度m=size(Utx,2)
%输出U0x，0阶模态，可以看做定常平均值
%输出An：时间变量，对应模态的幅值随时间的变化，可以用来做时间序列分析
%输出phiU：POD的模态
%输出Ds：特征值Ds反映了每一个模态对应的能量，可以用来排序
N=size(Utx,1);%时间
m=size(Utx,2);%空间

%0阶
U0x=mean(Utx,1);%空间平均
Utx=Utx-U0x.*ones(N,m);%低版本Matlab用Utx=Utx-(ones(N,1)*U0x).*ones(N,m); 代替
Uxt=Utx';
C=(Uxt'*Uxt);
[AU,D] = eig(C);%phiU是基函数，也是POD模态
%排序
Ds=diag(D)';
[~,ind]=sort(Ds,'descend');
AU=AU(:,ind);
Ds=Ds(ind);
%特征函数
phiU=Uxt*AU./sqrt(Ds);%低版本Matlab用phiU=Uxt*AU./(ones(m,1)*sqrt(Ds));代替
An=Uxt'*phiU;
end


function SHOW_POD_2(U0x,PhiU,Ds,x)
Limit_Y=[-2,2];
figure()

%4个模态图
subplot('Position',[0.08,0.79,0.45,0.16])%平均0阶
plot(x,U0x)
ylim(Limit_Y)
title('0阶模态/平均值')

subplot('Position',[0.08,0.54,0.45,0.16])%1阶模态
plot(x,PhiU(:,1))
title('1阶模态')

subplot('Position',[0.08,0.30,0.45,0.16])%2阶模态
plot(x,PhiU(:,2))
title('2阶模态')

subplot('Position',[0.08,0.05,0.45,0.16])%3阶模态
plot(x,PhiU(:,3))
title('3阶模态')

%能量分布
Ds_N=Ds/sum(Ds);
Cum_Ds_N=cumsum(Ds_N);
%N_Cum_95=sum((Cum_Ds_N<0.95));
N_Cum_95=10;
subplot('Position',[0.6,0.79,0.3,0.17])%总的能量分布
bar( 1:N_Cum_95 , Cum_Ds_N(1:N_Cum_95) ,'BarWidth',1)
ylim([0,1]);

subplot('Position',[0.65,0.54,0.3,0.17])%1阶模态能量占比
pie([Ds_N(1),1-Ds_N(1)],{[num2str(100*Ds_N(1),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])

subplot('Position',[0.65,0.30,0.3,0.17])%2阶模态能量占比
pie([Ds_N(2),1-Ds_N(2)],{[num2str(100*Ds_N(2),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])

subplot('Position',[0.65,0.05,0.3,0.17])%3阶模态能量占比
pie([Ds_N(3),1-Ds_N(3)],{[num2str(100*Ds_N(3),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])
end

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

计算结果如下，和之前2.1原始POD的计算结果完全一致。事实上，POD分解的结果也不应该随算法不同而不同，使用快照POD的目的只是为了加快计算速度减小内存，不影响最终结果。

另外说明一点，有人可能会说，你这第2模态，在2.2节和2.1节的对比明显一正一负不一样，为什么说模态相同？我想说POD模态的大小和正负不能说明什么，因为那是它的时间属性，由时间项A决定。对比模态的时候应该对比模态的波形、频率等信息。所以如果两个模态正负号相反，则恰恰意味着是相同的。实在觉得变扭，后期对比的时候乘一个负号就行。

注：感谢VTgrm大佬的评论建议，我大概看懂了，然而距离写这篇文章时间久远，所以暂时不对代码进行改动了（挖个坑，以后想想办法）。这里贴一下他的评论：
U0x=mean(Utx,1); %空间平均 Utx=Utx-U0x.*ones(N,m); %消除平均值 这里减去U0x是为了 减去第一个mode。 但是在snapshot方法中，为了计算协方差矩阵，,根据协方差定义，还应当减去 U0t，保证相乘的行列是centered. 其中U0t = mean(Utx,2); 当然最后重构的时候，U0x, U0t都要再加回来。

1.3 基于SVD的POD分解

之前介绍过SVD的基础知识，详情可以参见第0.2节。
如果看懂了我之前介绍的SVD知识，可能在前几节介绍POD分解时，就有一种想法呼之欲出了：能不能用SVD分解来简化之前的那些步骤？

比如下面这个常常在POD里出现的式子，结合特征向量和SVD之间的关系，就可以直接计算出特征向量V。
$$\left(A^{T}A\right)\cdot V=D\cdot V$$
所以基于SVD的POD分解就可以表示为：
$$\left[U,S,V\right]=\text{svd}\left(U_{tx}\right)$$
这里V就是模态矩阵。
时间项An可以计算为：
$$An=U\cdot S$$
模态的能量可以通过奇异值计算得到：
$$D_i={S_i}^2$$
这样POD分解所有的信息就已经集齐了。

事实上我们还可以得到：
$$U\cdot S\cdot V^{\prime }=An\cdot V^{\prime }=U_{tx}=\sum A_i\left(t\right)\cdot {\varphi }_i\left(x\right)$$
本质上POD分解就是SVD分解，POD分解的模态本质上就是SVD分解的数据压缩。POD分解中，前几阶模态能量最大，最能够反映信号特征，和之前演示的SVD分解中保留最大的奇异值就能还原矩阵是同样的道理。因此，可以说模态就是SVD分解的物理解释，SVD压缩就是POD分解的数学含义。

基于SVD的POD分解对应的Matlab代码如下：

%POD

clear
close all
%0初始化
x=0:0.02:10;
t=0:0.02:5-0.02;
Fs=1/(t(2)-t(1));
[X,T]=meshgrid(x,t);
%1构建信号
q=1.6*sin(2*pi*(X+2*T))+0.5*sin(2*pi*(3*X+4*T))+0.1;
N=size(T,1);%时间长度
m=size(X,2);%空间长度

%POD分解

%[U0x,An,PhiU,Ds]=POD_CLASS(q);%原始POD（在N远大于m时用可以加快速度节省内存）

%[U0x,An,PhiU,Ds]=POD_SNAP(q);%快照POD（在N远小于m时用可以加快速度节省内存）
 
[U0x,An,PhiU,Ds]=POD_SVD(q);%基于SVD分解的POD

%POD演示

SHOW_POD_2(U0x,PhiU,Ds,x);%前3阶模态分析



function [U0x,An,PhiU,Ds]=POD_SVD(Utx)
%基于SVD分解的POD，输入输出与原始POD相同
%输入Utx，其中时间离散长度N=size(Utx,1)，空间离散长度m=size(Utx,2)
%输出U0x，0阶模态，可以看做定常平均值
%输出An：时间变量，对应模态的幅值随时间的变化，可以用来做时间序列分析
%输出phiU：POD的模态
%输出Ds：特征值Ds反映了每一个模态对应的能量，可以用来排序
N=size(Utx,1);%时间
m=size(Utx,2);%空间

%0阶
U0x=mean(Utx,1);%空间平均
Utx=Utx-U0x.*ones(N,m);%低版本Matlab用Utx=Utx-(ones(N,1)*U0x).*ones(N,m); 代替
%利用SVD的方式，进行POD分解（用econ加速计算）
[U,S,PhiU]=svd(Utx,'econ');%SVD里的V等价于之前的特征向量PhiU
An=U*S;
Ds=diag(S).^2/N;
end


function SHOW_POD_2(U0x,PhiU,Ds,x)
Limit_Y=[-2,2];
figure()

%4个模态图
subplot('Position',[0.08,0.79,0.45,0.16])%平均0阶
plot(x,U0x)
ylim(Limit_Y)
title('0阶模态/平均值')

subplot('Position',[0.08,0.54,0.45,0.16])%1阶模态
plot(x,PhiU(:,1))
title('1阶模态')

subplot('Position',[0.08,0.30,0.45,0.16])%2阶模态
plot(x,PhiU(:,2))
title('2阶模态')

subplot('Position',[0.08,0.05,0.45,0.16])%3阶模态
plot(x,PhiU(:,3))
title('3阶模态')

%能量分布
Ds_N=Ds/sum(Ds);
Cum_Ds_N=cumsum(Ds_N);
%N_Cum_95=sum((Cum_Ds_N<0.95));
N_Cum_95=10;
subplot('Position',[0.6,0.79,0.3,0.17])%总的能量分布
bar( 1:N_Cum_95 , Cum_Ds_N(1:N_Cum_95) ,'BarWidth',1)
ylim([0,1]);

subplot('Position',[0.65,0.54,0.3,0.17])%1阶模态能量占比
pie([Ds_N(1),1-Ds_N(1)],{[num2str(100*Ds_N(1),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])

subplot('Position',[0.65,0.30,0.3,0.17])%2阶模态能量占比
pie([Ds_N(2),1-Ds_N(2)],{[num2str(100*Ds_N(2),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])

subplot('Position',[0.65,0.05,0.3,0.17])%3阶模态能量占比
pie([Ds_N(3),1-Ds_N(3)],{[num2str(100*Ds_N(3),'%.1f'),'%'],['']});
colormap([1,0,0;1,0,0;0,0,1;0,0,1])
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

计算结果同之前2节，不再过多叙述。

基于SVD的POD方法其稳定性较好，对误差容忍度较高。比如基于SVD方法生成的特征值，由于是由奇异值平方得到的，所以不存在负号，而原始POD或快照POD的特征值都会出现负号。而且目前matlab的eig特征根函数还没有自动排序的选项，所以需要手动进行排序，而SVD就已经自动排序好了，算是一个懒人福利。但是如果考虑计算内存和速度的话，当空间离散点远远大于时间离散点时，应该用快照POD（更新一下，如果采用SVD的econ方法，可以大大加快计算速度，和快照pod的速度相当，所以用SVD方法也是可以的）。

1.4 关于POD模态的稳定性

POD分解具有较强的稳定性，对数据的容忍度非常高。一般情况，只要数据足够多，即使数据的质量比较差，也可以得到比较正确的POD的模态，但是时间项就不行了。接下来举几个例子。

首先是随机交换帧与帧的顺序，从数学上来看是完全不起作用的。随机交换帧完全不会影响最终的模态结果。这里我也不再展示了。
但是从应用角度来说，这说明，即使你的时间步长特别长的时候(超过信号变化频率)，只要取的数据量足够多，就可以得到相应的模态。甚至今天做完实验觉得数据量不多，明天保持空间域不变接着做也可以。但是这种大步长信号就不要分析频率谱相关的信息了，虽然POD对时间步长没什么要求，但是fft对采样频率有要求。

之后，比如，如果从一个时间序列中随机删除几帧，也不会对POD模态造成很大的影响。

下图就是我随机删除了30%的帧后，进行的POD分解模态。平均项有些变形，但是模态的波形、顺序、空间频率、能量占比等都没有受到太大影响。

对于混入错误或随机信号，对POD分解的结果影响也不大。

下图为混入了30%随机信号下，得到的POD分解模态图。

因为我总共的POD时间帧有150张，即使算上30%不能用的，我依然还有105张有效的时间帧，这还是完全在POD处理能力之下的。

2 二维信号POD分解

2.1 二维标量信号的POD分解

对于二维信号，其实只需要将二维空间压缩至一维，之后问题就转化为第一章的内容了。之后将分解出的模态再还原为二维即可。由于POD分解不受排列方式的改变而改变，所以并没有什么要求规定如何将二维空间压缩为一维，只要压缩和还原的方法一致即可，不会影响结果。我这里用的是matlab中的reshape，当然用ind2sub()之类的或者B=A(:)之类的方法也都可以。

下面以一个二维标量场为例，matlab的代码如下：

%二维POD分解
clear
clc
close all

x=-6:0.2:6;
y=-5:0.2:5;
t=0:0.05:6;
[X,Y,T]=meshgrid(x,y,t);
[Ny,Nx,Nt]=size(X);

%自定义流场,U是沿x方向的速度分量，V是y方向的
U0=-1*Y.^2+25;
V0=0*Y;%UV0不随时间变化，设为定常流场
U1=-5*sin(Y).*cos(2*pi/20*Y).*(0.1+exp(T/10));
V1=5*sin(X-T).*cos(2*pi/20*Y).*(0.1+exp(T/10));
U2=-1*cos(2*Y).*cos(2*pi/20*Y).*(0.2+exp(-T/3));
V2=1*cos(2*(X-3*T)).*cos(2*pi/20*Y).*(0.2+exp(-T/3));

U_Sum=U0+U1+U2;
V_Sum=V0+V1+V2;
P=1+sqrt(U0.^2+V0.^2)+sqrt(U1.^2+V1.^2)+sqrt(U2.^2+V2.^2);%随便定义了一个标量，不代表任何物理意义

%计算变量P
P_xt=Uxyt_to_Uxt(P);%把2维问题转化为1维问题
[U0x,An,PhiU,Ds]=POD_SVD(P_xt');%POD里是tx格式，所以需要转置一下

%SHOW_POD2D_1(U0x,An,PhiU,Ds,x,y,t,P_xt)%动态演示，效果不好没用上
SHOW_POD2D_2(U0x,PhiU,Ds,x,y)


function Uxt=Uxyt_to_Uxt(Uxyt)
%把3维矩阵的xyt压缩为xt
[Ny,Nx,Nt]=size(Uxyt);%这里是matlab的meshgrid定义导致的，x和y是反着的，注意。
Nxy=Ny*Nx;
Uxt=reshape(Uxyt,Nxy,Nt);
end

function [U0x,An,PhiU,Ds]=POD_SVD(Utx)
%基于SVD分解的POD，输入输出与原始POD相同
%输入Utx，其中时间离散长度N=size(Utx,1)，空间离散长度m=size(Utx,2)
%输出U0x，0阶模态，可以看做定常平均值
%输出An：时间变量，对应模态的幅值随时间的变化，可以用来做时间序列分析
%输出phiU：POD的模态
%输出Ds：特征值Ds反映了每一个模态对应的能量，可以用来排序
N=size(Utx,1);%时间
m=size(Utx,2);%空间

%0阶
U0x=mean(Utx,1);%空间平均
Utx=Utx-U0x.*ones(N,m);%低版本Matlab用Utx=Utx-(ones(N,1)*U0x).*ones(N,m); 代替
%利用SVD的方式，进行POD分解
[U,S,PhiU]=svd(Utx,'econ');%SVD里的V等价于之前的特征向量PhiU
An=U*S;
Ds=diag(S).^2/N;
end

function SHOW_POD2D_1(U0x,An,PhiU,Ds,x,y,t,Uxt)
%动态显示
figure()
[X,Y]=meshgrid(x,y);
Nx=length(x);
Ny=length(y);
Nt=length(t);

for k=1:Nt
clf
subplot(3,2,1)%原始
Uxyt=reshape(Uxt,Ny,Nx,Nt);
pcolor(X,Y,Uxyt(:,:,k));shading interp
title('原始数据')
caxis([0,35]);

subplot(3,2,3)%平均
Uxy0=reshape(U0x,Ny,Nx);
pcolor(X,Y,Uxy0);shading interp
title('平均数据')
caxis([0,35]);

subplot(3,2,4)%1阶
P1=An(k,1).*PhiU(:,1)';
P1_xy=reshape(P1,Ny,Nx);
pcolor(X,Y,P1_xy);shading interp
title('1阶模态')
caxis([-3,3]);

subplot(3,2,5)%2阶
P2=An(k,2).*PhiU(:,2)';
P2_xy=reshape(P2,Ny,Nx);
pcolor(X,Y,P2_xy);shading interp
title('2阶模态')
caxis([-3,3]);

subplot(3,2,6)%3阶
P3=An(k,3).*PhiU(:,3)';
P3_xy=reshape(P3,Ny,Nx);
pcolor(X,Y,P3_xy);shading interp
%caxis([])
title('3阶模')
caxis([-3,3]);

subplot('Position',[0.65,0.7,0.2,0.2])
N_En=2;
En=[Ds(1:N_En);sum(Ds)-sum(Ds(1:N_En))];
pie(En,[ones(1,N_En),1]) 
title('1阶与2阶模态能量占比','Position',[0,1.6,0])

pause(0.1)
end

end

function SHOW_POD2D_2(U0x,PhiU,Ds,x,y)
[X,Y]=meshgrid(x,y);
Nx=length(x);
Ny=length(y);
figure()

%4个模态图
ax1=subplot('Position',[0.08,0.79,0.45,0.16]);%平均0阶
Uxy0=reshape(U0x,Ny,Nx);
pcolor(X,Y,Uxy0);shading interp
title('0阶模态/平均值')

ax3=subplot('Position',[0.08,0.54,0.45,0.16]);%1阶模态
Uxy1=reshape(PhiU(:,1),Ny,Nx);
pcolor(X,Y,Uxy1);shading interp
title('1阶模态')
ColorLimit=caxis;
caxis([-max(abs(ColorLimit)),max(abs(ColorLimit))]);

ax5=subplot('Position',[0.08,0.30,0.45,0.16]);%2阶模态
Uxy2=reshape(PhiU(:,2),Ny,Nx);
pcolor(X,Y,Uxy2);shading interp
title('2阶模态')
ColorLimit=caxis;
caxis([-max(abs(ColorLimit)),max(abs(ColorLimit))]);

ax7=subplot('Position',[0.08,0.05,0.45,0.16]);%3阶模态
Uxy3=reshape(PhiU(:,3),Ny,Nx);
pcolor(X,Y,Uxy3);shading interp
title('3阶模态')
ColorLimit=caxis;
caxis([-max(abs(ColorLimit)),max(abs(ColorLimit))]);

%能量分布
Ds_N=Ds/sum(Ds);
Cum_Ds_N=cumsum(Ds_N);
N_Cum=10;
ax2=subplot('Position',[0.6,0.79,0.3,0.17]);%总的能量分布
bar( 1:N_Cum , Cum_Ds_N(1:N_Cum) ,'BarWidth',1)
ylim([0,1]);

ax4=subplot('Position',[0.65,0.54,0.3,0.17]);%1阶模态能量占比
pie([Ds_N(1),1-Ds_N(1)],{[num2str(100*Ds_N(1),'%.1f'),'%'],['']});

ax6=subplot('Position',[0.65,0.30,0.3,0.17]);%2阶模态能量占比
pie([Ds_N(2),1-Ds_N(2)],{[num2str(100*Ds_N(2),'%.1f'),'%'],['']});


ax8=subplot('Position',[0.65,0.05,0.3,0.17]);%3阶模态能量占比
pie([Ds_N(3),1-Ds_N(3)],{[num2str(100*Ds_N(3),'%.1f'),'%'],['']});

colormap([[ones(8,1),linspace(0,7/8,8)',linspace(0,7/8,8)'];[1,1,1];[linspace(7/8,0,8)',linspace(7/8,0,8)',ones(8,1)]])
colormap(ax1,parula);
%用到一个小技巧，就是关于单独更改颜色条。饼状图的颜色也遵守colormap，但是我正好借了标量图的颜色条了。
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167

这里标量场是随意定的。可以看到前3阶模态就几乎覆盖了全部的能量。

2.2 二维矢量场的POD分解

对于二维矢量场，和之前二维标量场的思路完全相同。但是，由于我们认为速度U和速度V是耦合关系，所以需要把U和V合并为一个标量UV来同时考虑。合并方法直接采用UV=[U,V]方式，也可以每一个点进行混合合并，但最终结果都是将数据扩大为2倍，而且对模态分解没有影响，只要能够还原回去即可。

matlab代码如下：

%二维POD分解
clear
clc
close all

%定义流场时间和空间信息
x=-8:0.2:8;
y=-5:0.2:5;
t=0:0.05:6;
[X,Y,T]=meshgrid(x,y,t);
[Ny,Nx,Nt]=size(X);

%自定义流场,U是沿x方向的速度分量，V是y方向的
U0=-1*Y.^2+25;
V0=0*Y;%UV0不随时间变化，设为定常流场
U1=-5*sin(Y).*cos(2*pi/20*Y).*(0.1+exp(T/10));
V1=5*sin(X-T).*cos(2*pi/20*Y).*(0.1+exp(T/10));
U2=-1*cos(2*Y).*cos(2*pi/20*Y).*(0.2+exp(-T/3));
V2=1*cos(2*(X-3*T)).*cos(2*pi/20*Y).*(0.2+exp(-T/3));

U_Sum=U0+U1+U2;
V_Sum=V0+V1+V2;

%1计算UV向量
U_xt=Uxyt_to_Uxt(U_Sum);%把2维问题转化为1维问题
V_xt=Uxyt_to_Uxt(V_Sum);%把2维问题转化为1维问题
%然后把UV向量合并
UV_xt=[U_xt;V_xt];
%之前的这些都属于数据准备和整理部分

%POD
%这里空间离散点数远大于时间离散点，用快照POD
%[UV0x,An,PhiUV,Ds]=POD_SNAP(UV_xt');%POD里是tx格式，所以xt格式需要转置一下
[UV0x,An,PhiUV,Ds]=POD_SVD(UV_xt');%也可以对比试一试SVD
SHOW_POD_2D_UV(UV0x,PhiUV,Ds,x,y)


function Uxt=Uxyt_to_Uxt(Uxyt)
%把3维矩阵的xyt压缩为xt
[Ny,Nx,Nt]=size(Uxyt);%这里是matlab的meshgrid定义导致的，x和y是反着的，注意。
Nxy=Ny*Nx;
Uxt=reshape(Uxyt,Nxy,Nt);
end

function [U0x,An,PhiU,Ds]=POD_SVD(Utx)
%基于SVD分解的POD，输入输出与原始POD相同
%输入Utx，其中时间离散长度N=size(Utx,1)，空间离散长度m=size(Utx,2)
%输出U0x，0阶模态，可以看做定常平均值
%输出An：时间变量，对应模态的幅值随时间的变化，可以用来做时间序列分析
%输出phiU：POD的模态
%输出Ds：特征值Ds反映了每一个模态对应的能量，可以用来排序
N=size(Utx,1);%时间
m=size(Utx,2);%空间

%0阶
U0x=mean(Utx,1);%空间平均
Utx=Utx-U0x.*ones(N,m);%低版本Matlab用Utx=Utx-(ones(N,1)*U0x).*ones(N,m); 代替
%利用SVD的方式，进行POD分解
[U,S,PhiU]=svd(Utx,'econ');%SVD里的V等价于之前的特征向量PhiU
An=U*S;
Ds=diag(S).^2/N;
end

function [U0x,An,phiU,Ds]=POD_SNAP(Utx)
%快照POD，输入输出与原始POD相同
%输入Utx，其中时间离散长度N=size(Utx,1)，空间离散长度m=size(Utx,2)
%输出U0x，0阶模态，可以看做定常平均值
%输出An：时间变量，对应模态的幅值随时间的变化，可以用来做时间序列分析
%输出phiU：POD的模态
%输出Ds：特征值Ds反映了每一个模态对应的能量，可以用来排序
N=size(Utx,1);%时间
m=size(Utx,2);%空间

%0阶
U0x=mean(Utx,1);%空间平均
Utx=Utx-U0x.*ones(N,m);%低版本Matlab用Utx=Utx-(ones(N,1)*U0x).*ones(N,m); 代替
Uxt=Utx';
C=(Uxt'*Uxt);
[AU,D] = eig(C);%phiU是基函数，也是POD模态
%排序
Ds=diag(D)';
[~,ind]=sort(Ds,'descend');
AU=AU(:,ind);
Ds=Ds(ind);
%特征函数
phiU=Uxt*AU./sqrt(Ds);%低版本Matlab用phiU=Uxt*AU./(ones(m,1)*sqrt(Ds));代替
An=Uxt'*phiU;
end


function SHOW_POD_2D_UV(UV0x,PhiUV,Ds,x,y)
[X,Y]=meshgrid(x,y);
Nx=length(x);
Ny=length(y);
figure()
set(gcf,'position',[100 100 370 450])
%4个模态图
ax1=subplot('Position',[0.08,0.79,0.45,0.16]);%平均0阶
[Uxy0,Vxy0]=UV2UxyVxy(UV0x,Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxy0,Vxy0));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxy0(1:5:end,1:5:end),Vxy0(1:5:end,1:5:end),'color','k')
hold off
axis equal
title('0阶模态/平均值')

ax3=subplot('Position',[0.08,0.54,0.45,0.16]);%1阶模态
[Uxy1,Vxy1]=UV2UxyVxy(PhiUV(:,1),Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxy1,Vxy1));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxy1(1:5:end,1:5:end),Vxy1(1:5:end,1:5:end),'color','k')
hold off
axis equal
title('1阶模态')
ColorLimit=caxis;
caxis([-max(abs(ColorLimit)),max(abs(ColorLimit))]);

ax5=subplot('Position',[0.08,0.30,0.45,0.16]);%2阶模态
[Uxy2,Vxy2]=UV2UxyVxy(PhiUV(:,2),Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxy2,Vxy2));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxy2(1:5:end,1:5:end),Vxy2(1:5:end,1:5:end),'color','k')
hold off
axis equal
title('2阶模态')
ColorLimit=caxis;
caxis([-max(abs(ColorLimit)),max(abs(ColorLimit))]);

ax7=subplot('Position',[0.08,0.05,0.45,0.16]);%3阶模态
[Uxy3,Vxy3]=UV2UxyVxy(PhiUV(:,3),Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxy3,Vxy3));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxy3(1:5:end,1:5:end),Vxy3(1:5:end,1:5:end),'color','k')
hold off
axis equal
title('3阶模态')
ColorLimit=caxis;
caxis([-max(abs(ColorLimit)),max(abs(ColorLimit))]);



%能量分布
Ds_N=Ds/sum(Ds);
Cum_Ds_N=cumsum(Ds_N);
N_Cum=10;
ax2=subplot('Position',[0.6,0.79,0.3,0.17]);%总的能量分布
bar( 1:N_Cum , Cum_Ds_N(1:N_Cum) ,'BarWidth',1)
ylim([0,1]);

ax4=subplot('Position',[0.65,0.54,0.3,0.17]);%1阶模态能量占比
pie([Ds_N(1),1-Ds_N(1)],{[num2str(100*Ds_N(1),'%.1f'),'%'],['']});

ax6=subplot('Position',[0.65,0.30,0.3,0.17]);%2阶模态能量占比
pie([Ds_N(2),1-Ds_N(2)],{[num2str(100*Ds_N(2),'%.1f'),'%'],['']});


ax8=subplot('Position',[0.65,0.05,0.3,0.17]);%3阶模态能量占比
pie([Ds_N(3),1-Ds_N(3)],{[num2str(100*Ds_N(3),'%.1f'),'%'],['']});

colormap([[ones(8,1),linspace(0,7/8,8)',linspace(0,7/8,8)'];[1,1,1];[linspace(7/8,0,8)',linspace(7/8,0,8)',ones(8,1)]])
end


function [Uxy,Vxy]=UV2UxyVxy(UVx,Ny,Nx)
Ux=UVx(1:Ny*Nx);
Vx=UVx(Ny*Nx+1:end);
Uxy=reshape(Ux,Ny,Nx);
Vxy=reshape(Vx,Ny,Nx);
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169

这里有限推荐使用SVD-POD函数（注：这里指的是采用econ选项的SVD，采用‘econ’选项只需要不到1s，如果不采用这个选项，会花费13s）。同时也可以使用快照POD，也是不到1s的时间就可以计算完毕。因为这里需要处理的矩阵时间长度只有121，但是空间长度变成了2 * 51 * 81=8262，如果用的是原始算法的POD，计算时间将会远远大于SNAP-POD和SVD-POD。计算结果如下：
这里我绘制了不同模态的涡量图。