一级倒立摆控制 —— MPC 控制器设计及 MATLAB 实现_一级倒立摆系统建模matlab

系列文章目录

最优控制介绍
一级倒立摆控制 —— 系统建模（传递函数模型与状态空间方程表示）
一级倒立摆控制 —— PID 控制器设计及 MATLAB 实现
一级倒立摆控制 —— 最优控制 线性二次型控制（LQR）及 MATLAB 实现
一级倒立摆控制 —— MPC 控制器设计及 MATLAB 实现
一级倒立摆控制 —— ROS2 仿真
一级倒立摆控制 —— LQR 控制器 GAZEBO 仿真

---

前言

本例使用模型预测控制器 (MPC) 控制小车上的倒立摆。

---

一、摆杆 / 小车

本例中的被控对象是以下小车/摆杆组件，其中 $x$ 为小车位置，$\theta$ 为摆锤角度。

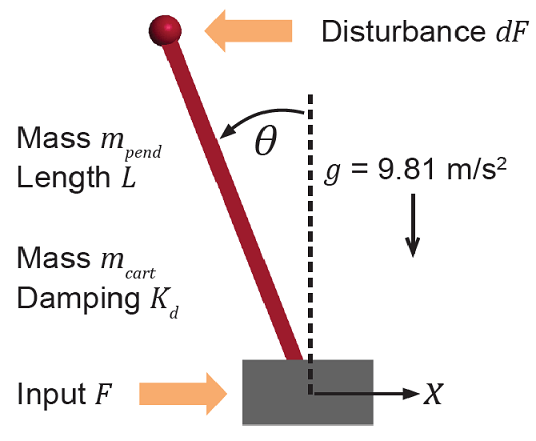
该系统通过对小车施加可变力 $F$ 进行控制。控制器需要在将小车移动到新位置时，或在倒立摆上端施加脉冲干扰 $dF$ 推动摆锤前进时，保持摆锤直立。

该被控对象在 Simulink® 中使用常用模块建模。

mdlPlant = 'mpc_pendcartPlant';
load_system(mdlPlant)
open_system([mdlPlant '/Pendulum and Cart System'],'force')
1
2
3

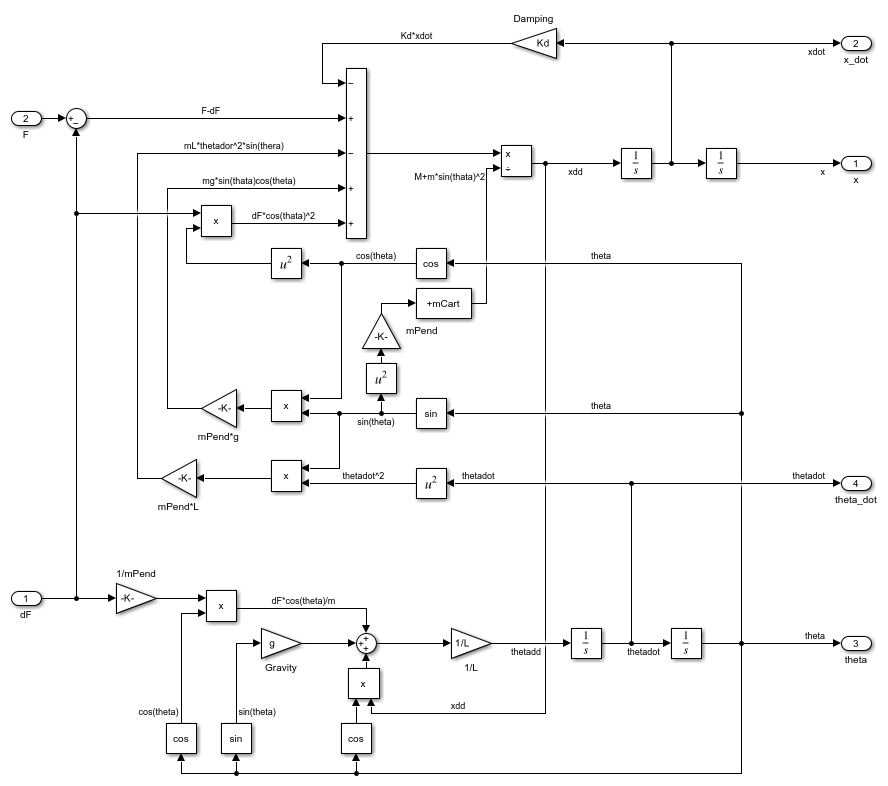
该 Simulink 主要描述倒立摆系统的动力学模型。

---

二、控制目标

假设小车/摆杆组件的初始条件如下：

• 小车在 x = 0 处静止。

• 倒立摆静止在直立位置 theta = 0。

控制目标为：

• 小车可以通过设定点的阶跃变化移动到 -10 和 10 之间的新位置。

• 在跟踪这种设定点变化时，上升时间应小于 4 秒（以保证性能），过冲应小于 5%（以保证稳健性）。

• 当对摆锤施加幅度为 2 的脉冲干扰时，小车应返回原位，最大位移为 1。 摆锤也应返回直立位置，峰值角位移为 15 度（0.26 弧度）。

直立位置是倒立摆的一个不稳定平衡位置，这使得控制任务更具挑战性。

---

三、控制结构

在本示例中，使用单个 MPC 控制器：

• 一个操纵变量： 变量力 $F$。

• 两个测量输出： 小车位置 $x$ 和摆角 $\theta$。

• 一个非测量干扰： 脉冲干扰 $dF$。

mdlMPC = 'mpc_pendcartImplicitMPC';
open_system(mdlMPC)
1
2

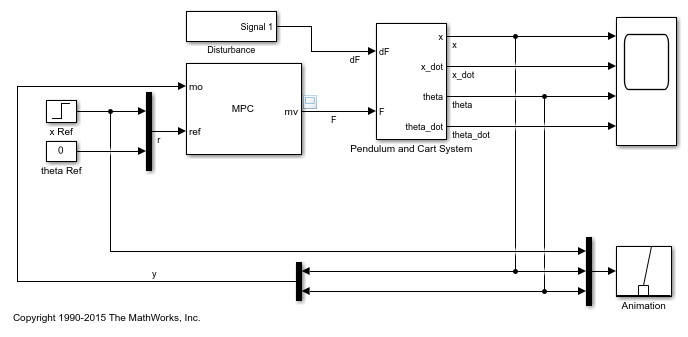
虽然小车速度 $\dot{x}$ 和摆杆角速度 $\dot{\theta }$ 可从被控对象模型中获得，但为了使设计案例更加真实，它们不作为 MPC 测量值。

当小车位置设定点变化时（步进输入），摆锤角度设定点是恒定的（0 = 直立位置）。

四、被控对象的线性模型

由于 MPC 控制器需要线性时不变（LTI）模型进行预测，因此在初始运行点对 Simulink 被控对象模型进行线性化。

指定线性化输入和输出点。

io(1) = linio([mdlPlant '/dF'],1,'openinput');
io(2) = linio([mdlPlant '/F'],1,'openinput');
io(3) = linio([mdlPlant '/Pendulum and Cart System'],1,'openoutput');
io(4) = linio([mdlPlant '/Pendulum and Cart System'],3,'openoutput');
1
2
3
4

为被控对象的初始条件创建运行点规范。

opspec = operspec(mdlPlant);
1

第一个状态是小车位置 $x$，已知初始状态为 0。

opspec.States(1).Known = true;
opspec.States(1).x = 0;
1
2

第三个状态是已知初始状态为 0 的摆角 $\theta$。

opspec.States(3).Known = true;
opspec.States(3).x = 0;
1
2

使用这些设置计算工作点。

options = findopOptions('DisplayReport',false);
op = findop(mdlPlant,opspec,options);
1
2

获取指定运行点的线性被控对象模型。

plant = linearize(mdlPlant,op,io);
plant.InputName = {'dF';'F'};
plant.OutputName = {'x';'theta'};
1
2
3

检查线性化被控对象的极点。

damp(plant)
1

                                                       
    极点           阻尼             频率            时间常量     
                           (rad/seconds)    (seconds)  
                                                       
  0.00e+00    -1.00e+00       0.00e+00            Inf  
 -3.21e+00     1.00e+00       3.21e+00       3.11e-01  
  5.13e+00    -1.00e+00       5.13e+00      -1.95e-01  
 -1.19e+01     1.00e+00       1.19e+01       8.40e-02  
1
2
3
4
5
6
7
8

检查线性化被控对象的零点（如果有的话）。

tzero(plant)
1

ans =

  空的 0×1 double 列向量
1
2
3

被控对象有一个积分器，一个不稳定极点，没有零点。

显示伯德图

bode(plant)
1

被控对象有一个积分器和一个不稳定极。

bdclose(mdlPlant)
1

五、MPC 控制器设计

被控对象有两个输入，即 $dF$ 和 $F$，以及两个输出，即 $x$ 和 $\theta$。在本例中，$dF$ 被指定为 MPC 控制器使用的未测量扰动，以便更好地抑制扰动。设置被控对象信号类型。

plant = setmpcsignals(plant,'ud',1,'mv',2);
1

要控制不稳定的被控对象，控制器的采样时间不能太大（干扰抑制能力差），也不能太小（计算量过大）。同样，预测范围也不能太长（被控对象的不稳定模式将占主导地位）或太短（违反约束条件的情况将无法预见）。本例使用以下参数：

Ts = 0.01;
PredictionHorizon = 50;
ControlHorizon = 5;
mpcobj = mpc(plant,Ts,PredictionHorizon,ControlHorizon);
1
2
3
4

-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000.
-->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000.
-->"Weights.OutputVariables" is empty. Assuming default 1.00000.
   for output(s) y1 and zero weight for output(s) y2 
1
2
3
4

对小车施加多大的力是有限制的，这是对被操控变量 F 的硬约束。

mpcobj.MV.Min = -200;
mpcobj.MV.Max = 200;
1
2

在设计权重之前，最好先对被控对象的输入和输出进行缩放。在本例中，由于被控变量的范围比被控对象的输出范围大两个数量级，因此应将 MV 输入量缩放 100。

mpcobj.MV.ScaleFactor = 100;
1

为提高控制器的鲁棒性，将 MV 变化率的权重从 0.1 提高到 1。

mpcobj.Weights.MVRate = 1;
1

要实现平衡性能，可调整被控对象输出上的权重。第一个权重与推车位置 $x$ 有关，第二个权重与角度 $\theta$ 有关。

mpcobj.Weights.OV = [1.2 1];
1

要实现更积极的干扰抑制，可通过将默认干扰模型增益乘以 10 倍来增加状态估计器增益。

更新输入干扰模型。

disturbance_model = getindist(mpcobj);
setindist(mpcobj,'model',disturbance_model*10);
1
2

-->Converting model to discrete time.
-->The "Model.Disturbance" property is empty:
   Assuming unmeasured input disturbance #1 is integrated white noise.
   Assuming no disturbance added to measured output #1.
-->Assuming output disturbance added to measured output #2 is integrated white noise.
-->"Model.Noise" is empty. Assuming white noise on each measured output.
1
2
3
4
5
6

更新输出干扰模型

disturbance_model = getoutdist(mpcobj);
setoutdist(mpcobj,'model',disturbance_model*10);
1
2

-->Converting model to discrete time.
   Assuming no disturbance added to measured output #1.
-->Assuming output disturbance added to measured output #2 is integrated white noise.
-->"Model.Noise" is empty. Assuming white noise on each measured output.
1
2
3
4

计算闭环的稳态输出灵敏度

cloffset(mpcobj)
1

ans = 2×2    
    0.0000   12.5735
   -0.0000    1.0000
1
2
3

第一列接近零的事实表明，对小车位置（第一输出）施加的恒定扰动可被闭环完全恢复。另一方面，第二列显示，施加在 $\theta$ 上的恒定扰动通过闭环时未受任何影响，并对小车位置产生了很大影响 (12.57)。换句话说，虽然闭环能够补偿位置干扰（或等同于跟踪位置参考），但却无法补偿测量角度的恒定干扰（或等同于跟踪恒定参考角度）。

六、闭环仿真

在 Simulink 中进行闭环仿真，验证 MPC 设计。

open_system([mdlMPC '/Scope'])
sim(mdlMPC)
1
2

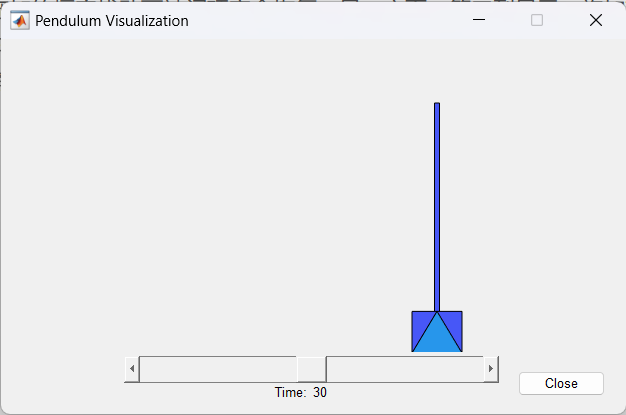
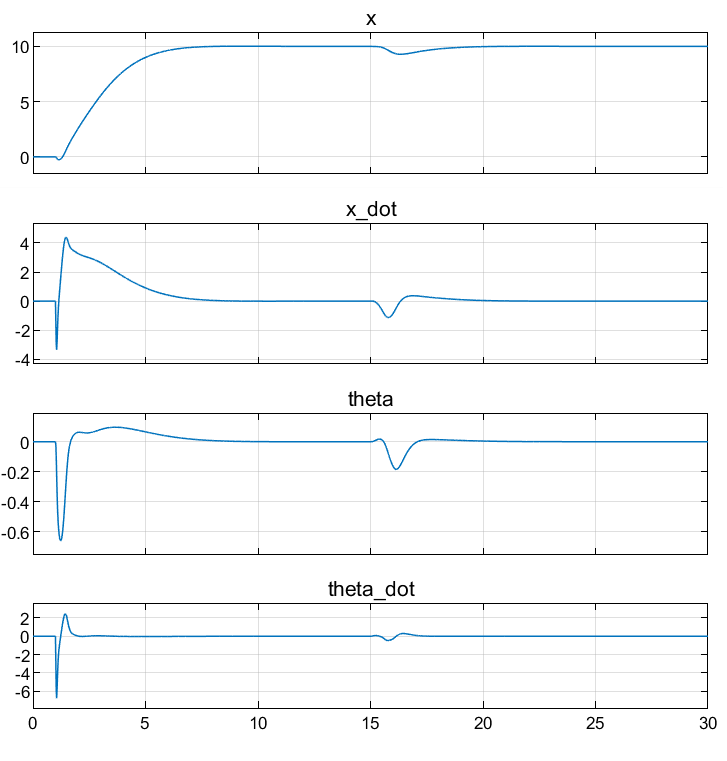
在非线性模拟中，所有控制目标都顺利实现。

七、讨论

需要指出的是，所设计的 MPC 控制器有其局限性。例如，如果将步进设定值变化增加到 15，摆锤在过渡期间就无法恢复直立位置。

为了在相同的上升时间内达到更长的距离，控制器在开始时对小车施加了更大的力。因此，摆锤从直立位置偏离的角度更大，如 60 度。在这种角度下，被控对象的动态与在 $\theta =0$ 时获得的 LTI 预测模型有很大差异。因此，对被控对象行为的预测误差超出了内置 MPC 鲁棒性所能处理的范围，控制器无法正常工作。

避免摆锤坠落的一个简单变通方法是，通过在 theta 上添加软输出约束和降低约束软化的 ECR 权重来限制摆锤位移。

mpcobj.OV(2).Min = -pi/2;
mpcobj.OV(2).Max = pi/2;
mpcobj.Weights.ECR = 100;
1
2
3

然而，采用这些新的控制器设置后，已无法在所需的上升时间内达到更远的距离。换句话说，为了避免违反软输出约束，控制器的性能被牺牲了。

为了在相同的上升时间内达到更远的距离，控制器需要在不同角度建立更精确的模型，以提高预测能力。另一个小车上倒立摆的增益调度 MPC 控制实例展示了如何利用增益调度 MPC 实现更长距离的控制。

关闭 Simulink 模型。

bdclose(mdlMPC)
1

---