数据增加(data augmentation),作为一种深度学习中的常用手段,数据增加对模型的泛化性和准确性都有帮助。数据增加的具体使用方式一般有两种,一种是实时增加,比如在Caffe中加入数据扰动层,每次图像都先经过扰动操作,再去训练,这样训练经过几代(epoch)之后,就等效于数据增加。还有一种是更加直接简单一些的,就是在训练之前就通过图像处理手段对数据样本进行扰动和增加。
常见的扰动有:随机裁剪,随机旋转和随机颜色/明暗。
随机裁剪
在裁剪的时候考虑图像宽高比的扰动。在绝大多数用于分类的图片中,样本进入网络前都是要变为统一大小,所以宽高比扰动相当于对物体的横向和纵向进行了缩放,这样除了物体的位置扰动,又多出了一项扰动。只要变化范围控制合适,目标物体始终在画面内,这种扰动是有助于提升泛化性能的。实现这种裁剪的思路如下图所示:
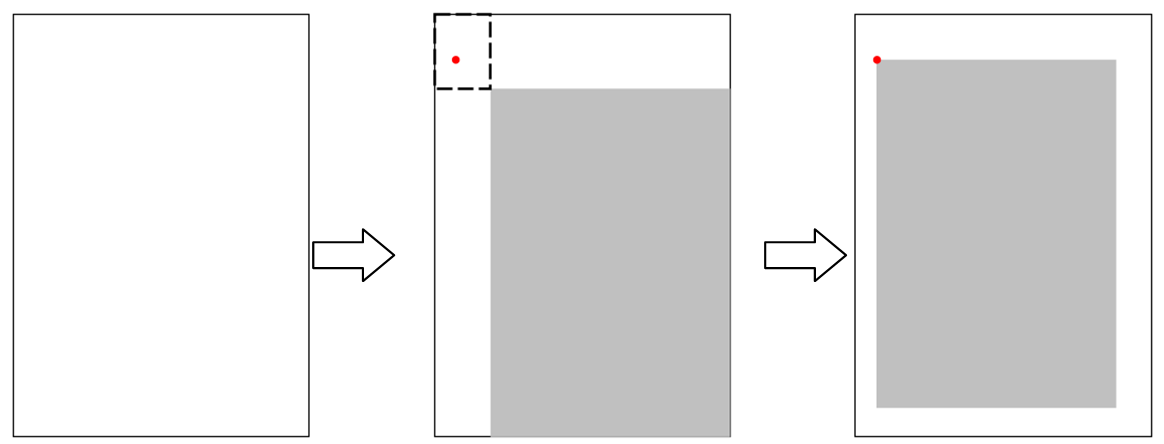
图中最左边是一幅需要剪裁的画面,首先根据这幅画面我们可以算出一个宽高比w/h。然后设定一个小的扰动范围δ和要裁剪的画面占原画面的比例β,从-到
之间按均匀采样,获取一个随机数
作为裁剪后画面的宽高比扰动的比例,则裁剪后画面的宽和高分别为:
想象一下先把这个宽为w’,高为h’的区域置于原画面的右下角,则这个区域的左上角和原画面的左上角框出的小区域,如图中的虚线框所示,就是裁剪后区域左上角可以取值的范围。所以在这个区域内随机采一点作为裁剪区域的左上角,就实现了如图中位置随机,且宽高比也随机的裁剪。
随机旋转
做数据增加时,一般希望旋转是沿着画面的中心。这样除了要知道旋转角度,还得计算平移的量才能让仿射变换的效果等效于旋转轴在画面中心,好在OpenCV中有现成的函数cv2.getRotationMatrix2D()可以使用。这个函数的第一个参数是旋转中心,第二个参数是逆时针旋转角度,第三个参数是缩放倍数,对于只是旋转的情况下这个值是1,返回值就是做仿射变换的矩阵。
直接用这个函数并接着使用cv2.warpAffine()会有一个潜在的问题,就是旋转之后会出现黑边。如果要旋转后的画面不包含黑边,就得沿着原来画面的轮廓做个内接矩形,该矩形的宽高比和原画面相同,如下图所示:
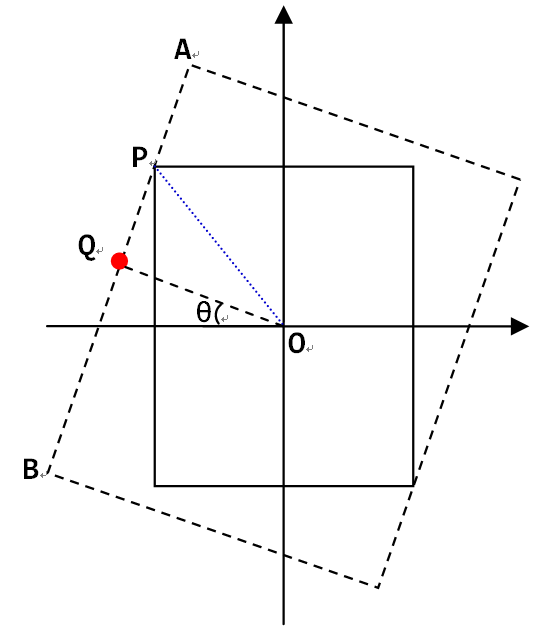
在图中,可以看到,限制内接矩形大小的主要是原画面更靠近中心的那条边,也就是图中比较长的一条边AB。因此我们只要沿着中心O和内接矩形的顶点方向的直线,求出和AB的交点P,就得到了内接矩形的大小。先来看长边的方程,考虑之前画面和横轴相交的点,经过角度-θ旋转后,到了图中的Q点所在:
因为长边所在直线过Q点,且斜率为1/tan(θ),所以有:
这时候考虑OP这条直线:
把这个公式带入再前边一个公式,求解可以得到:
注意到在这个问题中,每个象限和相邻象限都是轴对称的,而且旋转角度对剪裁宽度和长度的影响是周期(T=π)变化,再加上我们关心的其实并不是四个点的位置,而是旋转后要截取的矩形的宽w’和高h’,所以复杂的分区间情况也简化了,首先对于旋转角度,因为周期为π,所以都可以化到0到π之间,然后因为对称性,进一步有:
于是对于0到π/2之间的θ,有:
当然需要注意的是,对于宽高比非常大或者非常小的图片,旋转后如果裁剪往往得到的画面是非常小的一部分,甚至不包含目标物体。所以是否需要旋转,以及是否需要裁剪,如果裁剪角度多少合适,都要视情况而定。
随机颜色和明暗
给HSV空间的每个通道,分别加上一个微小的扰动。其中对于色调,从-到
之间按均匀采样,获取一个随机数
作为要扰动的值,然后新的像素值x’为原始像素值x +
;对于其他两个空间则是新像素值x’为原始像素值x的(1+
)倍,从而实现色调,饱和度和明暗度的扰动。
因为明暗度并不会对图像的直方图相对分布产生大的影响,所以在HSV扰动基础上,考虑再加入一个Gamma扰动,方法是设定一个大于1的Gamma值的上限γ,因为这个值通常会和1是一个量级,再用均匀采样的近似未必合适,所以从-logγ到logγ之间均匀采样一个值α,然后用
作为Gamma值进行变换。



