devbox
羊村懒王
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

社区发现 GN算法 fast betweeness算法 代码分析_社区发现算法girvan-newman实现

作者：羊村懒王 | 2024-03-20 16:36:25

赞

踩

社区发现算法girvan-newman实现

何谓社区发现

在社交网络分析与挖掘中，社区发现是一个常用且重要的应用。
俗话说，物以类聚，人以群分。社交网络中的节点也是一样。经常聚集成好几团。
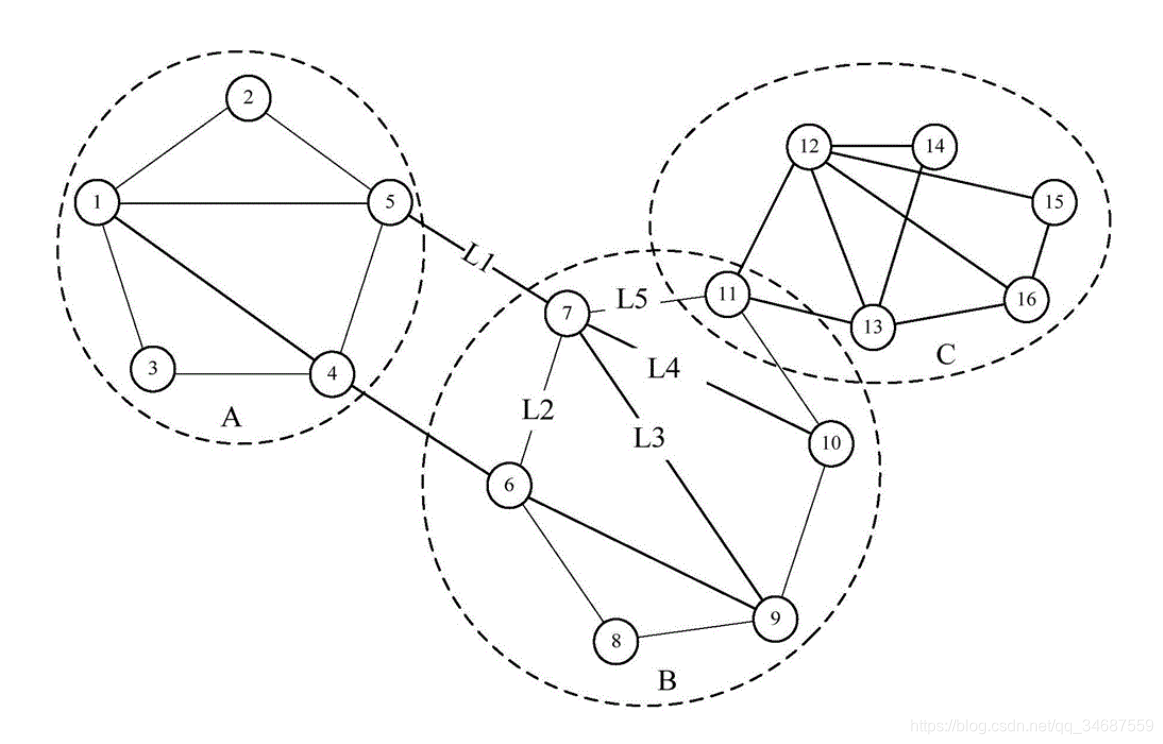
在这里插入图片描述
（上图来自百度）
如上图所示，可以分为3个节点簇A、B、C。这里便可以将每个簇称为社区。
可以看到其很明显的特征，社区里，各个节点的联系比较多；而社区之间，联系较少。

而社区发现，顾名思义，就是将社交网络中的社区给发现出来（似乎等于没说~~）

GN算法

GN算法是用于社区发现的算法。全程是Girvan Newman，是两位作者的名字组合。
该算法的大致思路是：
计算每条边的betweeness值，然后将该值最高的边删除，然后再重新的计算此时每天边的betweeness值，然后再删除最高的边，如此重复，直到连通分支数达到我们的要求为止。（连通分支就是社区了）

这里说一下什么是边的betweeness值，其实betweeness值就是该边的重要程度。我们知道社区之间的边比较少，那么我们如果找到社区之间的边，将其删掉，那不就是将社区给区分开了吗。
那怎么找到社区之间的边呢？用betweeness来衡量。从社区A到社区B的路会比较少，那么从社区A一点到社区B一点的最短路包含连接社区A到社区B的边的概率就会很高。
从而，我们用 c B ( e ) = ∑ s , t ∈ V σ ( s , t ∣ e ) σ ( s , t ) c_B(e) =\sum_{s,t \in V} \frac{\sigma(s, t|e)}{\sigma(s, t)} cB​(e)=∑s,t∈V​σ(s,t)σ(s,t∣e)​这样一个公式来计算Betweeness。其中 V V V 是节点集合, σ ( s , t ) \sigma(s, t) σ(s,t) 是最短路的个数 ( s , t ) (s, t) (s,t)-paths, and σ ( s , t ∣ e ) \sigma(s, t|e) σ(s,t∣e)是经过 e e e 的最短路个数。

下面来个示意图，来帮助大家理解：
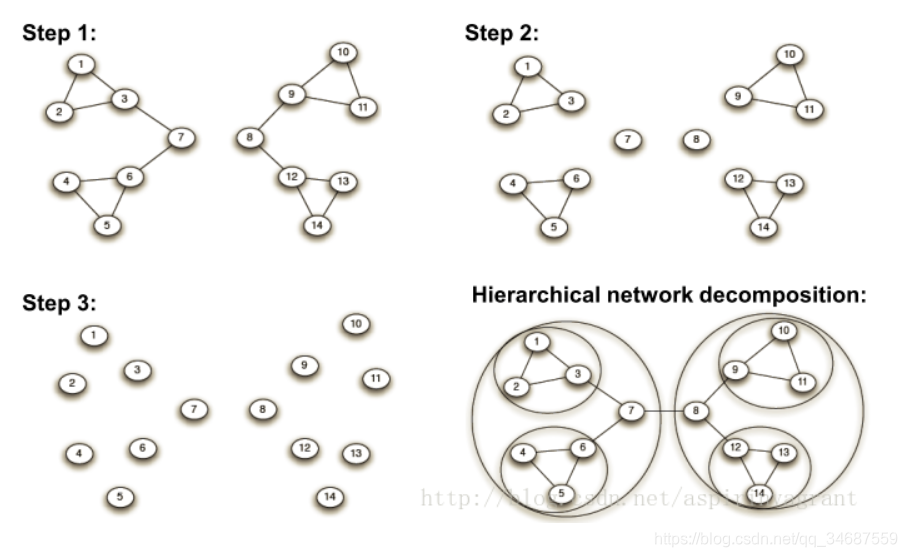
在这里插入图片描述
（上图来自https://blog.csdn.net/aspirinvagrant/article/details/45599071）
可以看到右下角是原始的模样，当然那个圈圈是后来画的，step1的适合，明显（7,8）是betweeness值最高的，将它删去之后，就很明显的能看出来左右两个连通分支，可以认为是两个社区，然后再算betweeness值，再删边，如此下去。

以上便是对GN算法的大致介绍。总的来说，就两点：

  • 计算betweeness值
  • 删边

但具体代码是怎么实现的呢，如何使用呢？下面我们来看代码加深理解。

GN算法代码

GN算法是一个比较经典的算法，所以有现成的模块来实现它。
本篇博客介绍的是networkx这个模块。大家可以pip install networkx来安装它。这个模块在社交网络中使用的很多。

首先来看如何使用networkx中的GN算法来进行社区发现。

import networkx as nx
from networkx.algorithms import community
import itertools

G = nx.karate_club_graph()
comp = community.girvan_newman(G)
# To stop getting tuples of communities once the number of communities is greater than k
k = 4
limited = itertools.takewhile(lambda c: len(c) <= k, comp)
for communities in limited:
    print(tuple(sorted(c) for c in communities)) 

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11

具体的使用可以看看它的源码，在源码中作者很清晰的写了多种用法，这里就不赘述了。

下面还是来看其如何实现的，讲讲我在看networkx实现GN算法的源码时的总结。
这里主要的就是community.girvan_newman(G)方法，我们进去看一下源码，这里因为作者注释的很好，我就不细讲各个参数是什么，而是讲一下它的实现思路。
代码如下：

def girvan_newman(G, most_valuable_edge=None):
    """Finds communities in a graph using the Girvan–Newman method.

    Parameters
    ----------
    G : NetworkX graph

    most_valuable_edge : function
        Function that takes a graph as input and outputs an edge. The
        edge returned by this function will be recomputed and removed at
        each iteration of the algorithm.

        If not specified, the edge with the highest
        :func:`networkx.edge_betweenness_centrality` will be used.

    Returns
    -------
    iterator
        Iterator over tuples of sets of nodes in `G`. Each set of node
        is a community, each tuple is a sequence of communities at a
        particular level of the algorithm.
    Notes
    -----
    The Girvan–Newman algorithm detects communities by progressively
    removing edges from the original graph. The algorithm removes the
    "most valuable" edge, traditionally the edge with the highest
    betweenness centrality, at each step. As the graph breaks down into
    pieces, the tightly knit community structure is exposed and the
    result can be depicted as a dendrogram.

    """
    # If the graph is already empty, simply return its connected
    # components.
    if G.number_of_edges() == 0:
        yield tuple(nx.connected_components(G))
        return
    # If no function is provided for computing the most valuable edge,
    # use the edge betweenness centrality.
    if most_valuable_edge is None:
        def most_valuable_edge(G):
            """Returns the edge with the highest betweenness centrality
            in the graph `G`.

            """
            # We have guaranteed that the graph is non-empty, so this
            # dictionary will never be empty.
            betweenness = nx.edge_betweenness_centrality(G)
            return max(betweenness, key=betweenness.get)
    # The copy of G here must include the edge weight data.
    g = G.copy().to_undirected()
    # Self-loops must be removed because their removal has no effect on
    # the connected components of the graph.
    g.remove_edges_from(nx.selfloop_edges(g))
    while g.number_of_edges() > 0:
        yield _without_most_central_edges(g, most_valuable_edge)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55

这里girvan newman 方法中有个参数most_valuable_edge，它是来计算边的值。你可以自定义计算规则，也可以不写，默认会计算我们之前所说的betweeness值。
可以看其实整个girvan newman的运行逻辑就是最后两行：

while g.number_of_edges() > 0:
        yield _without_most_central_edges(g, most_valuable_edge)

  • 1
  • 2

前面去掉自环，判断 什么的不用管。直接看最后两行。这是一个while循环。它每一步是执行_without_most_central_edges(g, most_valuable_edge)方法，看名字我们可以知道，这是去掉最中心的边，同时还把betweeness计算方法给传进去了。所以这个方法我们可以推断，它是计算betweeness，然后将最大的边给删掉，不断循环。
回忆一下，这不就是我们之前提到的GN算法的全过程吗。是的，这就是GN算法实现的大的逻辑。
说一下，这里返回的是生成器，是所有社区的集合。

那下面我们肯定要看一下_without_most_central_edges(g, most_valuable_edge)这个方法了，它是具体怎么做的。

def _without_most_central_edges(G, most_valuable_edge):
    original_num_components = nx.number_connected_components(G)
    num_new_components = original_num_components
    while num_new_components <= original_num_components:
        edge = most_valuable_edge(G)
        G.remove_edge(*edge)
        new_components = tuple(nx.connected_components(G))
        num_new_components = len(new_components)
    return new_components

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9

该方法我们主要看while循环里面的，它是调用most_valuable_edge(G)方法计算出betweeness，选出该值最大的边，然后将这个边删掉。后面的生成元组我们就不关心了，这里的核心就是计算betweeness（删边操作比较简单嘛）。
所以看了这个方法之后，我们发现，总体的代码逻辑都很简单，主要是调用了most_valuable_edge(G)这个方法。好那我们继续去看看这个方法。

        def most_valuable_edge(G):
            """Returns the edge with the highest betweenness centrality
            in the graph `G`.

            """
            # We have guaranteed that the graph is non-empty, so this
            # dictionary will never be empty.
            betweenness = nx.edge_betweenness_centrality(G)
            return max(betweenness, key=betweenness.get)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9

不过似乎这里就只从已经算好的边的betweeness中找到最大的。所以这还没到重点，怎么算betweeness呢？我们继续看nx.edge_betweenness_centrality(G)这个方法的源码。

def edge_betweenness_centrality(G, k=None, normalized=True, weight=None,
                                seed=None):
    r"""Compute betweenness centrality for edges.
    Betweenness centrality of an edge $e$ is the sum of the
    fraction of all-pairs shortest paths that pass through $e$
    """
    betweenness = dict.fromkeys(G, 0.0)  # b[v]=0 for v in G
    # b[e]=0 for e in G.edges()
    betweenness.update(dict.fromkeys(G.edges(), 0.0))
    if k is None:
        nodes = G
    else:
        nodes = seed.sample(G.nodes(), k)
    for s in nodes:
        # single source shortest paths
        if weight is None:  # use BFS
            S, P, sigma = _single_source_shortest_path_basic(G, s)
        else:  # use Dijkstra's algorithm
            S, P, sigma = _single_source_dijkstra_path_basic(G, s, weight)
        # accumulation
        betweenness = _accumulate_edges(betweenness, S, P, sigma, s)
    # rescaling
    for n in G:  # remove nodes to only return edges
        del betweenness[n]
    betweenness = _rescale_e(betweenness, len(G), normalized=normalized,
                             directed=G.is_directed())
    return betweenness


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28

来讲一下这里的大致逻辑。我们主要关注一下的代码，其他的细枝末节不是很重要，不关系到算法逻辑。

for s in nodes:
        # single source shortest paths
        if weight is None:  # use BFS
            S, P, sigma = _single_source_shortest_path_basic(G, s)
        else:  # use Dijkstra's algorithm
            S, P, sigma = _single_source_dijkstra_path_basic(G, s, weight)
        # accumulation
        betweenness = _accumulate_edges(betweenness, S, P, sigma, s)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

这是一个for循环，nodes我们将当做是nodes=G.nodes的情况。
首先，是调用单源最短路算法（无权重用BFS，有权重用Dijkstra）。
返回的S是s节点能够到达的节点，P是对应到达节点的最短路径的字典，而sigma是到各个点的最短距离。
获得了这些之后呢，调用_accumulate_edges(betweenness, S, P, sigma, s)方法来计算betweeness值。好终于出现计算它的了。
我们再进入该方法看看源码。

def _accumulate_edges(betweenness, S, P, sigma, s):
    delta = dict.fromkeys(S, 0)
    while S:
        w = S.pop()
        coeff = (1 + delta[w]) / sigma[w]
        for v in P[w]:
            c = sigma[v] * coeff
            if (v, w) not in betweenness:
                betweenness[(w, v)] += c
            else:
                betweenness[(v, w)] += c
            delta[v] += c
        if w != s:
            betweenness[w] += delta[w]
    return betweenness


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

可以看到，这里基本就是公式，但是你会发现，这和我们之前说的betweeness的计算公式不一样呀。我们之前的公式不是 c B ( e ) = ∑ s , t ∈ V σ ( s , t ∣ e ) σ ( s , t ) c_B(e) =\sum_{s,t \in V} \frac{\sigma(s, t|e)}{\sigma(s, t)} cB​(e)=∑s,t∈V​σ(s,t)σ(s,t∣e)​，这里咋还有个 δ \delta δ呢，这是从哪来的。
我重新看了edge_betweenness_centrality方法的注释，发现在注释的最后，它参考了A Faster Algorithm for Betweenness Centrality这篇论文，我没有去找这篇论文，而是找了一篇博客来看，终于基本上看懂了为什么这里的代码逻辑和我们的公式不一样了。

如果从betweeness的定义直接出发来计算betweeness，它的复杂度十分之大，所以Ulrik Brandes就在A Faster Algorithm for Betweenness Centrality一文中提出了快速计算betweeness的方法，使得复杂度大大下降。
之后很多GN方法的实现就采用了该方法。

总结一下，计算一条边的Betweeness值，其实就是计算所有节点对的最短路径经过边e的条数/最短路径数。也就是判断最短路径经过e的比例，从而来判断e是否是属于沟通两个社区的“桥梁”。
经过使用快速Betweeness计算，最终将公式转换成了 ∑ w : v ∈ P s ( w ) σ s v σ s w ( 1 + δ s ( w ) ) \sum_{w:v\in P_{s}(w)} \frac{\sigma_{sv}}{\sigma_{sw}} (1+\delta_{s}(w)) ∑w:v∈Ps​(w)​σsw​σsv​​(1+δs​(w))（这是计算其他节点对v节点的依赖性，也就是betweeness的计算）。对比代码看看，是不是一样呢。可以说代码完全是按照fast betweeness 的计算公式来的。

具体的推导过程我就不写了，毕竟是看了别人的博客才弄懂，也懒得搬运过来，尊重他人的成果。博客写的挺好的，我看了挺久，照着推了一遍，大致是可以理解最终的公式是怎么来的了，感兴趣的强烈建议去看一下。
上链接：网络的介数中心性(betweenness)及计算方法

Modularity

Modularity（模块度）是用来衡量社区划分质量的一种方法。
它的计算公式是
。
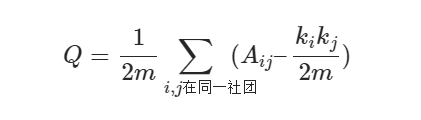
其中 1 2 m ∑ i , j A i j \frac{1}{2m}\sum_{i,j}A_{ij} 2m1​∑i,j​Aij​就表示 社团内部实际的边数的比例。
而 1 2 m ∑ i j k i k j 2 m \frac{1}{2m}\sum_{ij} \frac{k_{i}k_{j}}{2m} 2m1​∑ij​2mki​kj​​就表示 随机情况下社团内部期望的边数的比例。
因此，Modularity的定义可以看做：
在社区内部的边的比例，减去边随机放置时社区内部期望边数的比例。

在networkx中也有对应的实现，我们可以通过调用方法来衡量社区划分的质量。
例如：

import networkx as nx
import itertools
from networkx.algorithms import community

G = nx.karate_club_graph()
comp = community.girvan_newman(G)
k = 4
limited = itertools.takewhile(lambda c: len(c) <= k, comp)
for communities in limited:
    # print(list(set(sorted(c)) for c in communities))
    communities = list(set(sorted(c)) for c in communities)
    print(community.modularity(G,communities))

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12

这里community.modularity(G,communities)的第一参数是将网络输入，第二个参数是输入诸如[{0, 1, 2}, {3, 4, 5}]，社区集合的列表。

我们运行一下，看看使用GN算法进行的社区划分的质量：
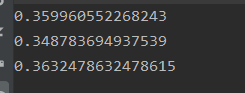
在这里插入图片描述
这里Modularity范围是[-0.5,1]，越靠近1越好。

参考资料

这里参考了两篇比较好的博客，对于理解fast betweeness的计算和Modularity的计算有很大帮助。

  • https://blog.csdn.net/betarun/article/details/51168259?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-2
  • http://www.yalewoo.com/modularity_community_detection.html
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/275058
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号