基于傅里叶变换的顺序无关透明算法_次序无关透明度

以前讨论过相关OIT算法并用Vulkan实现过一种基于GPU并行链表的OIT，但无论是深度剥离或并行链表虽然可以实现顺序无关透明，但使用的显存及时间显然很费，确切的来说很难在项目中实际使用。

一般引擎中常用基于加权的OIT，此算法虽然仅使用两趟pass即可解决大部分问题，但准确性却是存在一些小问题（毕竟符合计算机图形学一大定律：看着正确就行…），无意间发现一篇国外19年发布于可视化会议上的论文：Fourier Opacity Optimization for Scalable Exploration，本篇文章巧妙的使用数学方法解决透明度的问题，并且效率与占用比上述方法都是有过之无不及（但本方法因为使用的是傅里叶展开，所以是一种有偏的算法）。

一、半透明混合的渲染方程

首先需要明确一点，为什么半透明物体的混合会和顺序有关系，你可以从以前的这篇文章中基于GPU并行链表的OIT直观了解，也可以根据如下混合公式：

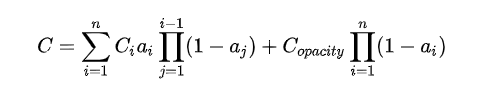
其中 Copacity 为不透明物体的颜色，可以理解为透明物体的底图；在前一部分里面，aj 为第 j 个片段的透明度，并且第 j 个片段的深度小于第 i 个片段的深度。因此对于混合颜色过程中任意一个颜色 Ci ，都需要知道所有深度小于他的透明度 aj 才能进行混合，这也是为什么半透明混合会和顺序有关系。

为了后面方便，论文中将公式的前面一部分进行变形：

其中 T(di) 为光学深度，为了和物理量保持一致特地添加负号（实现过程中可以不用刻意添加这个负号），其中 di 为当前片元（Fragment）的线性深度，n为一个像素的n个半透明片段。

由于只有 T(di) 与顺序有关系，接下来的重点处理 T(di) 。

1.1 光学深度

在物理学中，光学深度或光学厚度是指通过材料的入射辐射功率与透射辐射功率之比的自然对数。

因此，光学深度越大，穿过材料的透射辐射功率量越小。具体定义可参照维基中介绍：

也可以查看B站的视频教程：【天文学名词第2期】光学深度。

二、傅里叶变换

傅里叶变换和我们在球谐光照里面讲到的一样，对于复杂的函数，我们可以通过各种方法比如泰勒展开，球谐展开将一个复杂的函数展开成简单的函数如：

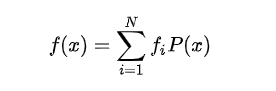
fi 为系数（常数）， Pi(x) 为其他的函数，大家不用管 P 函数指什么，如果展开次数越多也就是 N 越大那么对 f(x) 的还原（拟合）就越好。

本质上目前的机器学习就是这种思想，对于未知的函数，通过去求他的每个系数 fi ，然后去逼近（拟合）函数 f(x) 。

而本文就是采用傅里叶展开。对于函数 f(x) 的傅里叶展开公式如下（傅里叶展开是通过正弦和余弦函数来作为基函数 Pi(x) ）：

对于一般的傅里叶级数的公式如下：

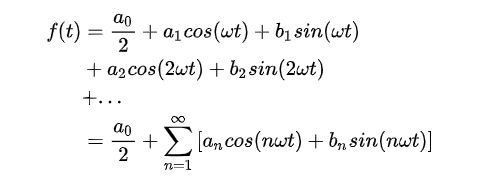
其中，

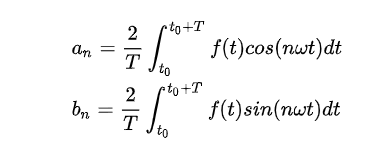
本文中将系数的周期设定为积分区间一般设为[0, 1]，因此n取2π，表达如下：

一旦采用傅里叶基函数来表示函数 f(x) ，那么对于 f(x) 在 (0,d) 上面的积分就非常容易计算（因为只有余弦函数和正弦函数，因此这也看得出来如果想求函数的积分，那么用傅里叶展开是一个非常好的选择）,具体积分表达式：

不过上述傅里叶展开怎样和函数 T(di) 建立联系呢？要知道 T(di) 只是一些离散值的求和，而上述式子中的 f(x) 又是什么呢？离散值求和与积分改怎么建立联系呢？下一部分将是本文的精妙之处。

三、联立求和与积分

3.1 狄拉克函数

狄拉克 δ函数 是一个广义函数，在物理学中常用其表示质点、点电荷等理想模型的密度分布，该函数在除了零以外的点取值都等于零，而其在整个定义域上的积分等于1。

狄拉克δ函数在概念上，它是这么一个“函数”：在除了零以外的点函数值都等于零，而其在整个定义域上的积分等于1。

我们需要根据狄拉克函数 δ(x) 的特点：仅仅在x=0处为正无穷，其余位置都是为0，因此可以推出如下性质：

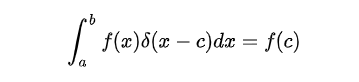
c为(a,b)上的一个点，可以看出来我们将函数与狄拉克函数乘积进行积分就变成了一个点的函数值。我们利用狄拉克函数构建一个新的函数：

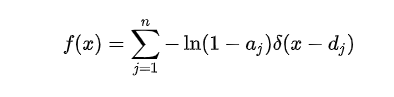
利用狄拉克函数的性质，我们在区域 [公式] 对上式进行积分，可以得到本文的重点等式：

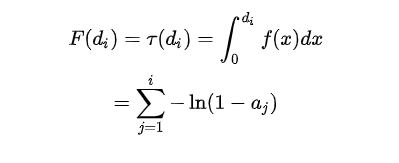
此时，我们构建了一个离散函数积分与求和的桥梁。

3.2 联立

接下来就只需要将上式的积分部分代入到下式

可得到：

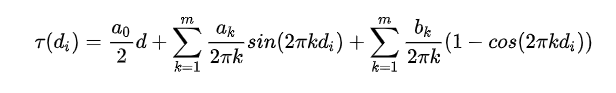
其中系数 ak,bk ，之前由于

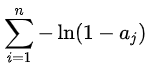
为离散值，因此不能直接进行积分，而引入狄拉克函数之后，利用其性质就得到了:

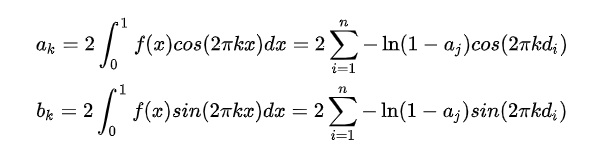
至此，推导部分全部结束。

3.3 分析

对于公式 T(di) ：

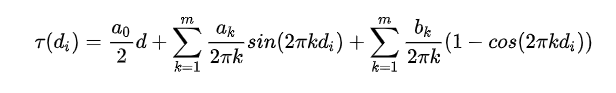
唯一的自变量只是当前片段的深度，其余都为常数。

对于系数 ak,bk ：

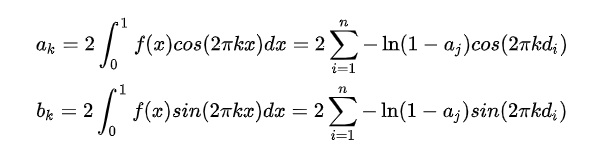
只需要当前像素n个片段计算之后值求和即可，与顺序无关。因此只需要单独一个Pass计算系数 ak,bk。

四、归一化

由于采用傅里叶展开拟合的函数会导致亮的部分更亮，暗的部分更暗，因此作者还提出了一种归一化方法，即将透明方程中第一部分公式由：

变为：

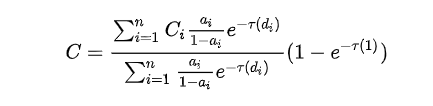
其中，

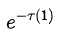
为当前像素中所有片段的值。

上述式子和前面的推导并不矛盾，我们傅里叶展开是为了计算 -T(di) ，因此只需要最后计算按照式上式即可。

五、代码实现

在代码中的具体渲染实现，我们主要分为三步：

1. 混合只是混合一个不透明片段之前的所有片段，因此首先需要得到一张不透明像素的深度图，用于告诉后面我们混合的最大深度是多少。
2. 然后一个Pass需要用于计算系数 ak,bk （对于系数需要计算多少个就看具体需要的精度，通常可以计算6个，两张纹理刚好可以存储），从其表达式中可以看出来系数是像素的n个片段之和，这里有个小技巧，我们可以利用图形API中的混合功能。因此只需要将两个混合因子设置为1，就变成了单纯的将两个值进行相加。
3. 在计算了系数 ak,bk 之后，只需要结合 T(di) 表达式和式归一化的 C 表达式就可以计算出当前像素最终的颜色值。注意式 T(di) ，这里虽然与顺序无关了，不过还是需要进行求和，我们可以像第二点一样，采用图形API混合功能来做求和（也可以自己写）。

5.1 不透明绘制

首先是不透明物体的绘制，其shader不再赘述。

顶点着色器：

#version 460  core
layout(location = 0) in vec3 _Position;
layout(location = 1) in vec3 _Normal;
layout(location = 2) in vec2 _TexCoord;

layout(std140, binding = 0) uniform u_Matrices4ProjectionWorld
{
	mat4 u_ProjectionMatrix;
	mat4 u_ViewMatrix;
};

uniform mat4 u_ModelMatrix;

out vec2 v2f_TexCoords;

void main()
{
	gl_Position = u_ProjectionMatrix * u_ViewMatrix * u_ModelMatrix * vec4(_Position, 1.0f);
	v2f_TexCoords = _TexCoord;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

片元着色器：

#version 460  core
in  vec2 v2f_TexCoords;

layout (location = 0) out vec4 Albedo_;

uniform sampler2D u_DiffuseTexture;
uniform vec4 u_DiffuseColor;

void main()
{
	vec3  Albedo = texture(u_DiffuseTexture, v2f_TexCoords).xyz;
	Albedo_ = vec4(Albedo,1.0);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

5.2 傅里叶级数

5.2.1 缓存 ak、bk

顶点着色器：

#version 460  core
layout(location = 0) in vec3 _Position;
layout(location = 1) in vec3 _Normal;
layout(location = 2) in vec2 _TexCoord;

layout(std140, binding = 0) uniform u_Matrices4ProjectionWorld
{
	mat4 u_ProjectionMatrix;
	mat4 u_ViewMatrix;
};

uniform mat4 u_ModelMatrix;

out vec2 v2f_TexCoords;

void main()
{
	vec4 FragPosInViewSpace = u_ViewMatrix * u_ModelMatrix * vec4(_Position, 1.0f);
	gl_Position = u_ProjectionMatrix * FragPosInViewSpace;
	v2f_TexCoords = _TexCoord;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

片元着色器：

#version 460  core
#define PI 3.1415926
in  vec2 v2f_TexCoords;

layout (location = 0) out vec4 CoefficientOne_;
layout (location = 1) out vec4 CoefficientTwo_;

uniform sampler2D u_OpacityTexture;
uniform vec4 u_DiffuseColor;
uniform float u_NearPlane;
uniform float u_FarPlane;

float LinearizeDepth(float vDepth)
{
	float z = vDepth * 2.0 - 1.0; 
	return (2.0 * u_NearPlane * u_FarPlane) / (u_FarPlane + u_NearPlane - z * (u_FarPlane - u_NearPlane));
}
void main()
{
    float opaqueDepth = texelFetch(u_OpacityTexture, ivec2(v2f_TexCoords.xy), 0).r;
	if (opaqueDepth != 0.0 && gl_FragCoord.z > opaqueDepth) discard;
	
	float a0 = -log(1.0 - u_DiffuseColor.a + 1e-5);
	float depth = LinearizeDepth(gl_FragCoord.z);

	float sin2, cos2, sin4, cos4, sin6, cos6, sin8, cos8, sin10, cos10, sin12, cos12, sin14, cos14;
	cos2 = cos(2 * PI * depth);
	sin2 = sin(2 * PI * depth);
	cos4 = cos2 * cos2 - sin2 * sin2;
	sin4 = 2 * cos2 * sin2;
	cos6 = cos4 * cos2 - sin4 * sin2;
	sin6 = sin4 * cos2 + cos4 * sin2;
	float a1 = a0 * cos2;
	float b1 = a0 * sin2;
	float a2 = a0 * cos4;
	float b2 = a0 * sin4;
	float a3 = a0 * cos6;
	float b3 = a0 * sin6;

	CoefficientOne_ = vec4(1,a0,a1,b1);
	CoefficientTwo_ = vec4(a2,b2,a3,b3);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

5.2.2 求解 T(di)、Ci

本部分主要根据公式

求解具体的 Ci ：

顶点着色器：

#version 460  core
layout(location = 0) in vec3 _Position;
layout(location = 1) in vec3 _Normal;
layout(location = 2) in vec2 _TexCoord;

layout(std140, binding = 0) uniform u_Matrices4ProjectionWorld
{
	mat4 u_ProjectionMatrix;
	mat4 u_ViewMatrix;
};

uniform mat4 u_ModelMatrix;

out vec2 v2f_TexCoords;

void main()
{
	vec4 FragPosInViewSpace = u_ViewMatrix * u_ModelMatrix * vec4(_Position, 1.0f);
	gl_Position = u_ProjectionMatrix * FragPosInViewSpace;
	v2f_TexCoords = _TexCoord;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

片元着色器：

#version 460  core
#define PI 3.1415926
in  vec2 v2f_TexCoords;

layout (location = 0) out vec4 Color_;

uniform sampler2D u_CoefficientOneTex;
uniform sampler2D u_CoefficientTwoTex;
uniform sampler2D u_OpacityTexture;
uniform vec4 u_DiffuseColor;
uniform float u_NearPlane;
uniform float u_FarPlane;

float LinearizeDepth(float vDepth)
{
	float z = vDepth * 2.0 - 1.0; 
	return (2.0 * u_NearPlane * u_FarPlane) / (u_FarPlane + u_NearPlane - z * (u_FarPlane - u_NearPlane));
}
void main()
{
    float opaqueDepth = texelFetch(u_OpacityTexture, ivec2(gl_FragCoord.xy), 0).r;
	if (opaqueDepth != 0.0 && gl_FragCoord.z > opaqueDepth) discard;
	
	float depth = LinearizeDepth(gl_FragCoord.z);

	vec4 fourierOne = texelFetch(u_CoefficientOneTex, ivec2(gl_FragCoord.xy), 0);
	vec4 fourierTwo = texelFetch(u_CoefficientTwoTex, ivec2(gl_FragCoord.xy), 0);

	float a0 = fourierOne.y;
	float a1 = fourierOne.z;
	float b1 = fourierOne.w;
	float a2 = fourierTwo.x;
	float b2 = fourierTwo.y;
	float a3 = fourierTwo.z;
	float b3 = fourierTwo.w;

	float sin2, cos2, sin4, cos4, sin6, cos6, sin8, cos8, sin10, cos10, sin12, cos12, sin14, cos14;
	cos2 = cos(2 * PI * depth);
	sin2 = sin(2 * PI * depth);
	cos4 = cos2 * cos2 - sin2 * sin2;
	sin4 = 2 * cos2 * sin2;
	cos6 = cos4 * cos2 - sin4 * sin2;
	sin6 = sin4 * cos2 + cos4 * sin2;

	float opticalDepth = 0.5 * a0 * depth;
	opticalDepth += (a1 / (2 * PI)) * sin2;
	opticalDepth += (b1 / (2 * PI)) * (1 - cos2);
	opticalDepth += (a2 / (4 * PI)) * sin4 ;
	opticalDepth += (b2 / (4 * PI)) * (1 - cos4);
	opticalDepth += (a3 / (6 * PI)) * sin6;
	opticalDepth += (b3 / (6 * PI)) * (1 - cos6);
	float transmittance = exp(-opticalDepth);
	Color_ = vec4(transmittance * u_DiffuseColor.xyz * u_DiffuseColor.a / (1.0 - u_DiffuseColor.a), 
	              transmittance * u_DiffuseColor.a / (1.0 - u_DiffuseColor.a));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

5.3 归一化颜色融合

本部分主要根据：

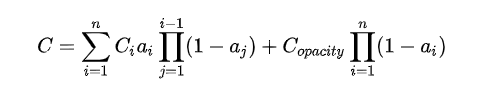
融合不透明物体与透明物体颜色：

顶点着色器：

#version 460  core

layout (location = 0) in vec2 _Position;
layout (location = 1) in vec2 _TexCoords;

out vec2 v2f_TexCoords;

void main()
{
	gl_Position = vec4(_Position, 0.0, 1.0);
	v2f_TexCoords = _TexCoords;
}
1
2
3
4
5
6
7
8
9
10
11
12

片元着色器：

#version 460  core
in  vec2 v2f_TexCoords;

layout (location = 0) out vec4 Color_;

uniform sampler2D u_OpacityAlbedoTexture;
uniform sampler2D u_TansparentTexture;
uniform sampler2D u_CoefficientOneTex;

void main()
{
   vec3  opaqueColor = texelFetch(u_OpacityAlbedoTexture, ivec2(gl_FragCoord.xy), 0).rgb;
   vec4  translucentColor = texelFetch(u_TansparentTexture, ivec2(gl_FragCoord.xy), 0).rgba;
   float totalOpticalDepth = 0.5 * texelFetch(u_CoefficientOneTex, ivec2(gl_FragCoord.xy), 0).y;
   float totalTransmittance = exp(-totalOpticalDepth);

   vec3 finalColor = translucentColor.rgb / translucentColor.a * (1.0 - totalTransmittance) + opaqueColor * totalTransmittance;
   if(isnan(finalColor.x))
	   finalColor = opaqueColor;
   Color_ = vec4(finalColor,1.0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21