【LeetCode热题100】105. 从前序与中序遍历序列构造二叉树（二叉树）

一.题目要求

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

二.题目难度

中等

三.输入样例

示例 1:

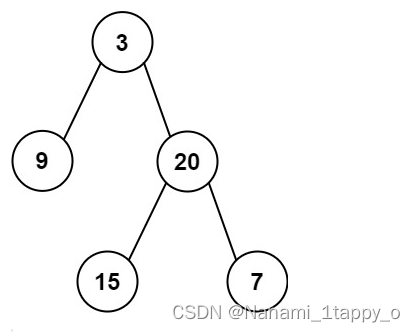
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

四.解题思路

没有思路 看GPT总结吧

五.代码实现

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return buildTreeHelper(preorder, 0, preorder.size(), inorder, 0, inorder.size());
    }

private:
    TreeNode* buildTreeHelper(vector<int>& preorder, int preStart, int preEnd, 
                              vector<int>& inorder, int inStart, int inEnd) {
        if (preStart >= preEnd || inStart >= inEnd) {
            return nullptr;
        }

        TreeNode* root = new TreeNode(preorder[preStart]);
        auto rootPos = find(inorder.begin() + inStart, inorder.begin() + inEnd, preorder[preStart]);
        int leftSize = rootPos - (inorder.begin() + inStart);

        root->left = buildTreeHelper(preorder, preStart + 1, preStart + 1 + leftSize, 
                                     inorder, inStart, inStart + leftSize);
        root->right = buildTreeHelper(preorder, preStart + 1 + leftSize, preEnd, 
                                      inorder, inStart + 1 + leftSize, inEnd);
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

六.题目总结

构造二叉树的问题可以通过递归的方法解决，核心思路是利用先序遍历和中序遍历的特性：

• 先序遍历（preorder）的特点是每次遍历的第一个元素都是当前子树的根节点。
• 中序遍历（inorder）的特点是根节点将树分为左子树和右子树，左子树的节点都在根节点的左边，右子树的节点都在根节点的右边。

解题步骤

• 步骤 1: 确定根节点

从先序遍历的数组中获取第一个元素，这个元素是当前子树的根节点。

• 步骤 2: 分割中序遍历数组

在中序遍历的数组中找到根节点的位置，这个位置将数组分为两部分：左子树的中序遍历和右子树的中序遍历。

• 步骤 3: 分割先序遍历数组

利用中序遍历中左子树的节点数，可以确定先序遍历数组中左子树和右子树的分界线。
第一个元素后面紧跟着的是左子树的先序遍历，接着是右子树的先序遍历。

• 步骤 4: 递归构建子树

使用步骤 2 和步骤 3 中确定的左右子树的先序遍历和中序遍历数组，递归地构建左子树和右子树。

• 步骤 5: 返回根节点

将构建好的左右子树分别连接到根节点的左右指针上，然后返回根节点。

示例
假设我们有以下先序遍历和中序遍历的数组：

• preorder = [3,9,20,15,7]
• inorder = [9,3,15,20,7]

先序遍历的第一个元素是3，所以3是根节点。
在中序遍历数组中找到3，它将数组分为两部分：

• [9]是左子树的中序遍历，[15,20,7]是右子树的中序遍历。

由于左子树在中序遍历中有1个节点，我们知道先序遍历数组中第一个元素之后的一个元素（9）是左子树的先序遍历；剩下的[20,15,7]是右子树的先序遍历。

• 对于左子树，先序遍历和中序遍历都只有一个元素[9]，这意味着左子树只有一个节点9。

• 对于右子树，我们重复上述过程，先序遍历[20,15,7]和中序遍历[15,20,7]，可以构建出右子树。

• 将构建好的左右子树连接到根节点3上。

通过这个过程，我们能够逐步构建出整棵树。