python机器学习-实现ID3决策树_id3算法的python实现

       ID3算法由Ross Quinlan在1986年提出，主要针对属性选择问题，是决策树算法中最具影响和典型的算法。

       ID3决策树可以有多个分支，但是它不能处理连续的特征值，如果要处理连续的特征值，必须将特征值离散化之后才能进行处理。ID3是一种Hunt算法，也就是一种贪心地生成决策树的算法，每一次所选取的划分数据集的划分属性都是当前情况的最优选择，也就是在ID3算法中，每一次所选择的都是此时样本集中具有最大信息熵增益值的属性作为划分属性来分割数据集，并按照该属性的所有取值来对数据集进行切分。也就是说，如果此时所选择的一个划分属性，有3种取值，那么数据集将被切分为3份，一旦按某属性切分后，该属性在之后的ID3算法的执行中，将不再使用。
       在建立决策树的过程中，根据划分属性来划分数据，使得原本“混乱”的数据集（也就是收集到的数据集，没有经过任何处理的原始数据集）的熵(混乱度，在此引用描述原始数据的混乱程度)减少。按照不同属性划分数据集，熵的减少的程度会不一样。ID3决策树算法选择熵减少程度最大的属性来划分数据集，也就是选择产生信息嫡增益最大的属性。这也就是ID3算法是Hunt算法的缘由，会在选择每一个划分属性时，计算所有属性的信息熵增益，并选择产生最大的信息熵增益的属性作为划分属性，注意，如果某一属性已经被选择作为了划分属性，那么，这一属性将不再参与接下来的划分属性选择。
        ID3算法的具体实现步骤如下：
    (1)对当前样本集合，计算所有属性的信息增益。
    (2)选择信息增益最大的属性作为划分样本集合的划分属性，把划分属性取值相同的样本划分为同一个子样本集。一旦按某属性划分后，该属性在之后的算法执行中，将不再使用。
    (3)若子样本集中所有的样本属于一个类别，则该子集作为叶子结点，并标上合适别号，并返回调用处；否则对子样本集递归调用本算法。
        递归划分停止的条件如下。
    (1)没有划分属性可供继续划分。
    (2)给定的分支的数据集为空。
    (3)数据集属于同一类。
    (4)决策树已经达到设置的最大值。

        ID3决策树实现：

        以如下数据集为例，

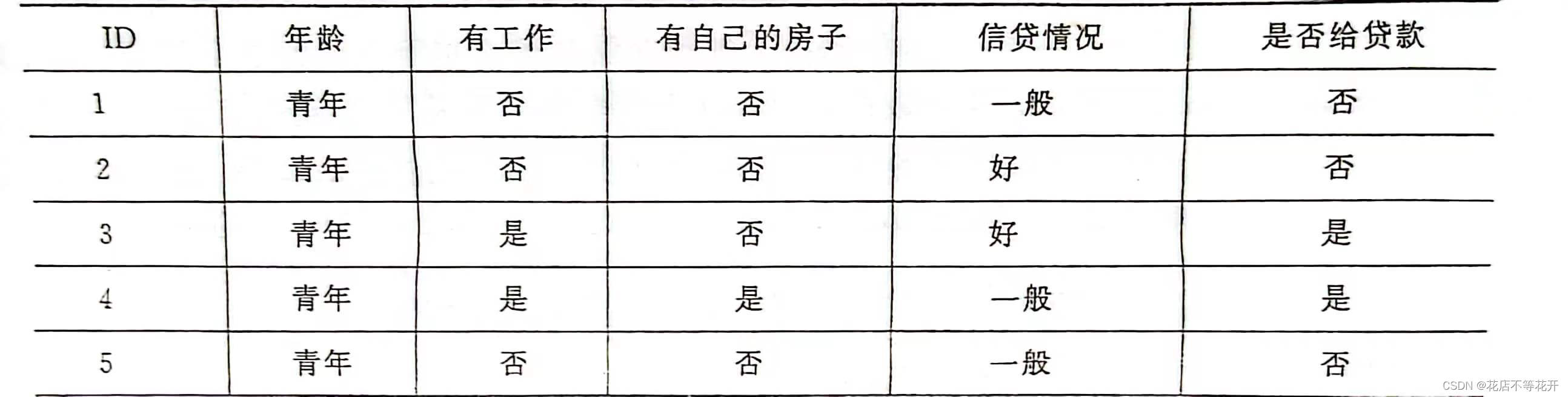
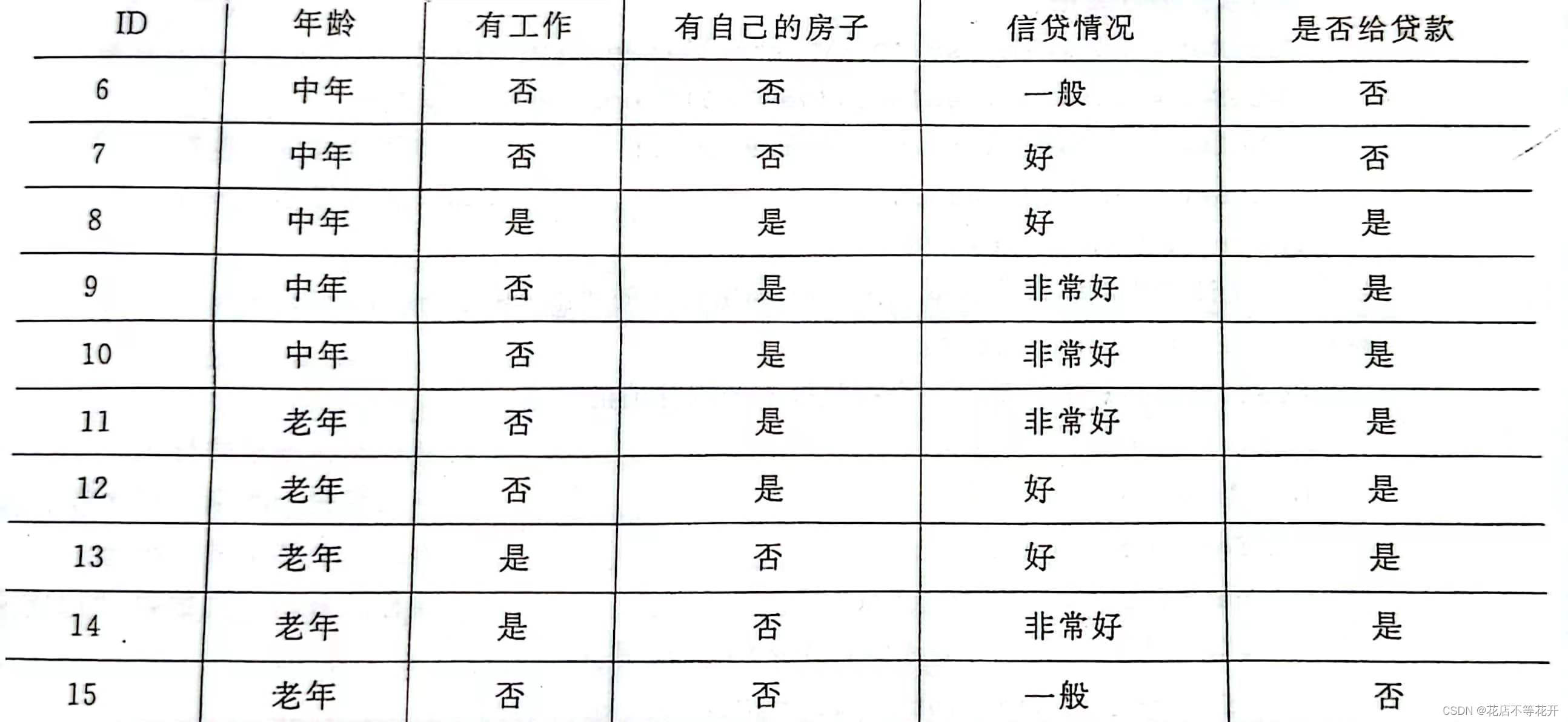
       由于数据都是文本型数据，在构建决策树前，先对数据集进行数值化预处理：
   (1)年龄：0代表青年，1代表中年，2代表老年。
  (2)有工作：0代表否，1代表是。
  (3)有自己的房子：0代表否，1代表是。
  (4)信贷情况：0代表一般，1代表好，2代表非常好。
  (5)类别(是否给贷款)：no代表否，yes代表是。 

        处理之后的数据如下：

age job  house     credit     class

0     0     0     0     no

0     0     0     1     no

0     1     0     1     yes

0     1     1     0     yes

0     0     0     0     no

1     0     0     0     no

1     0     0     2     no

1     1     1     1     yes

1     0     1     2     yes

1     0     1     2     yes

2     0     1     2     yes

2     0     1     1     yes

2     1     0     1     yes

2     1     0     2     yes

2     0     0     0     no

        1、加载数据集与计算信息熵 

import operator
import math
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import pydotplus
import pandas as pd
 
def loadDataSet():#读取存放样本数据的csv文件，返回样本数据集和划分属性集
    dataSet = pd.read_csv("C:\\Users\\86191\\Desktop\\贷款申请样本数据集.csv", delimiter=',')
    labeSet = list(dataSet.columns)[:-1]#得到划分属性集
    dataSet = dataSet.values#得到样本数据集
    return dataSet,labeSet
 
#计算样本数据集的信息熵
def calcShannonEnt(dataSet):#dataSet的每个元素是一个存放样本的属性值的列表
    numEntries = len(dataSet)#获取样本集个数
    labeCounts = {}#保存每个类别出现次数的字典
    for featVec in dataSet:#对每个样本进行统计
        currentLabel = featVec[-1]#取最后一列数据，即类别信息
        if currentLabel not in labeCounts.keys():
            labeCounts[currentLabel] = 0#添加字典元素，键值为0
        labeCounts[currentLabel] += 1#计算类别
    shannonEnt = 0.0#计算信息熵
    for key in labeCounts.keys():#keys()以列表返回一个字典所有的键
        prob = float(labeCounts[key])/numEntries#计算一个类别的概率
        shannonEnt -= prob*math.log(prob,2)
    return shannonEnt
 
dataSet,labeSet = loadDataSet()
print(dataSet)
print('数据集的信息熵:', calcShannonEnt(dataSet))

        输出结果如下，其中，第一个输出的是进行预处理之后的数据集，第二个则是计算的数据集的信息熵。

[[0 0 0 0 'no']
 [0 0 0 1 'no']
 [0 1 0 1 'yes']
 [0 1 1 0 'yes']
 [0 0 0 0 'no']
 [1 0 0 0 'no']
 [1 0 0 2 'no']
 [1 1 1 1 'yes']
 [1 0 1 2 'yes']
 [1 0 1 2 'yes']
 [2 0 1 2 'yes']
 [2 0 1 1 'yes']
 [2 1 0 1 'yes']
 [2 1 0 2 'yes']
 [2 0 0 0 'no']]
数据集的信息熵: 0.9709505944546686

        2、计算信息增益：

#按照给定特征划分数据集
def splitDataSet(dataSet,axis,value): #返回按照axis属性切分，该属性的值为value的子数据集，并把该属性及其值去掉
    retDataSet = []
    for featVec in dataSet:#dataSet的每个元素是一个样本，以列表表示，将相同特征值value的样本提取出来
        if featVec[axis] == value:  # 只把该属性上值是value的，加入到子数据集中
            reducedFeatVec = list(featVec[:axis])
            reducedFeatVec.extend(featVec[axis+1:])#extend()在列表list末尾一次性追加序列中的所有元素
            retDataSet.append(reducedFeatVec)
    return retDataSet#返回不含特征的子集
 
#按照最大信息增益划分数据集
def chooseBestFeatureToSplit(dataSet):  # 选择出用于切分的标签的索引值
    numberFeatures = len(dataSet[0])-1#计算标签数量
    baseEntropy = calcShannonEnt(dataSet) #计算数据集的信息熵
    bestInfoGain = 0.0#初始增益0
    bestFeature = -1#最优划分属性的索引值
    for i in range(numberFeatures):#按信息增益选择标签索引
        featList = [example[i] for example in dataSet]#取出所有样本的第i个标签值
        uniqueVals = set(featList)#将标签值列表转为集合
        newEntropy = 0.0
        for value in uniqueVals:#对于一个属性i，对每个值切分成的子数据集计算其信息熵，将其加和就是总的熵
            subDataSet = splitDataSet(dataSet,i,value)#划分后的子集
            prob = len(subDataSet) / float(len(dataSet))#根据公式计算属性划分数据集的熵值
            newEntropy += prob * calcShannonEnt(subDataSet)#根据公式计算属性划分数据集的熵
        infoGain = baseEntropy - newEntropy  # 计算信息增益
        print("第%d个划分属性的信息增益为%.3f"%(i,infoGain))
        if (infoGain > bestInfoGain):#获取最大信息增益
            bestInfoGain = infoGain#更新信息增益，找到最大的信息增益
            bestFeature = i#记录信息增益最大的特征的索引值
    return bestFeature#返回信息增益最大特征的索引值
 
print("最优索引值:"+str(chooseBestFeatureToSplit(dataSet)))

       将第1部分的加载数据集与计算信息熵的代码和这一代码合在一起整体运行，可求出
数据集的按信息增益最大划分数据集的最优划分属性，代码的运行结果如下。

第0个划分属性的信息增益为0.083
第1个划分属性的信息增益为0.324
第2个划分属性的信息增益为0.420
第3个划分属性的信息增益为0.249
最优索引值:2

        3、构建决策树

        ID3算法的核心是在决策树的各个结点上根据信息增益最大准则选择划分属性，递归地构建决策树，具体方法如下。
      (1)从根结点开始，对结点计算所有可能的划分属性的信息增益，选择信息增益最大的属性作为结点的名称，也即结点的类标记。
      (2)由该划分属性的不同取值建立子结点，再对子结点递归地调用以上方法，构建新的子结点；直到所有划分属性的信息增益均很小或没有划分属性可以选择为止。
      (3)最后得到一棵决策树。
       以数据集为例，在计算信息增益部分已经求得，“有自己的房子”划分属性的信息增益最大，所以选择“有自己的房子”作为根结点的名称，它将训练集划分为两个子集1(“有自己的房子”取值为“是”)和2(“有自己的房子”取值为“否”)。由于1只有同一类的样本点，所以它成为一个叶子结点，结点的类标记为“是”。对2则需要从特征：年龄、有工作和信贷情况中选择新的特征，然后计算各个特征的信息增益。

#构建决策树
def majorityCnt(classList):#计算出现次数最多的标签，并返回该标签值
    classCount = {}
    for vote in classList:#投票法统计每个标签出现多少次
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    print(classCount.items())
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)#对标签字典按值从大到小排序
    print(sortedClassCount)
    return sortedClassCount[0][0]#取已拍序的dic_items的第一个item的第一个值
 
def createTree(dataSet, labels):
    # 取出标签,生成列表
    classList = [example[-1] for example in dataSet]
    # 如果D中样本属于同一类别，则将node标记为该类叶节点
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 如果属性集为空或者D中样本在属性集上取值相同（意思是处理完所有特征后，标签还不唯一），
    # 将node标记为叶节点，类比为样本数量最多的类,这里采用字典做树结构，所以叶节点直接返回标签就行
    if len(dataSet[0]) == 1:  # 此时存在所有特征相同但标签不同的数据，需要取数量最多标签的作为叶子节点，数据集包含了标签，所以是1
        return majorityCnt(classList)  # 这种情况西瓜书中的属性集为空和样本集为空的情况
 
    bestFeat = chooseBestFeatureToSplit(dataSet)  # 选择最佳标签进行切分，返回标签索引
    bestFeatLabel = labels[bestFeat]  # 根据最佳标签索引取出该属性名
    myTree = {bestFeatLabel: {}}  # 定义嵌套的字典存放树结构
    del (labels[bestFeat])  # 属性名称列表中删除已选的属性名
    featVals = [example[bestFeat] for example in dataSet]  # 取出所有样本的最优属性的值
    uniqueVals = set(featVals)  # 将属性值转成集合，值唯一
    for value in uniqueVals:  # 对每个属性值继续递归切分剩下的样本
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree
 
tree = createTree(dataSet, labeSet)
print('生成的决策树:',tree)

         整体运行上述代码，输出结果如下：

第0个划分属性的信息增益为0.083
第1个划分属性的信息增益为0.324
第2个划分属性的信息增益为0.420
第3个划分属性的信息增益为0.249
第0个划分属性的信息增益为0.252
第1个划分属性的信息增益为0.918
第2个划分属性的信息增益为0.390
生成的决策树: {'house': {0: {'job': {0: 'no', 1: 'yes'}}, 1: 'yes'}}

        4、决策树的可视化

        下面将给出两种可视化方法，其中第一种方法使用sklearn.tree.DecisionTreeClassifier决策树模型实现数据集的决策树的构建与决策树的可视化，且需要安装Graphviz软件，结果是生成一个pdf文件；第二种方法则不需要，但并不生成pdf文件，而是图片。第一种方法的代码如下：

#可视化方法1
X=dataSet[:,0:4]
y=dataSet[:,4]
from sklearn import tree
clf = tree.DecisionTreeClassifier(criterion='entropy')
clf = clf.fit(X,y)
dot_data = tree.export_graphviz(clf,out_file= None,
                                feature_names=['age','job','house','credit'],
                                class_names=['no','yes'],
                                filled=True,rounded=True,
                                special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("贷款申请样本数据集.pdf")

        5、使用ID3决策树进行预测

        依靠训练数据构造了决策树之后，可以将它用于实际数据的分类。在执行数据分类时，需要决策树以及用于构造决策树的属性向量。然后，程序比较测试数据与决策树上的属性值，递归执行该过程直到进入叶子结点；最后将测试数据定义为叶子结点所属的类型。例如用上述已经训练好的决策树进行分类，只需要提供这个人是否有房子、是否有工作这两个信息即可。

#使用决策树预测
def classify(inputTree,featlables,testVec):
    firstStr = list(inputTree.keys())[0]
    secondDict = inputTree[firstStr]
    featIndex = featlables.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key],featlables,testVec)
            else:
                classLabel = secondDict[key]
    return classLabel
 
#测试数据
dataSet,labeSet =loadDataSet()
tree = createTree(dataSet,labeSet)
testVec=[0,0]
Labels=['house','job']
result = classify(tree,Labels,testVec)
if result == 'yes':
    print('决策树分类结果:放贷')
if result == 'no':
    print('决策树分类结果:不放贷')

        总结，ID3算法的缺点如下：
    (1)ID3算法采用了信息增益作为选择划分属性的标准，会偏向于选择取值较多的属性，也就是如果数据集中的某个属性值对不同的样本基本上是不相同的，更极端的情况，对于每个样本都是唯一的，如果用这个属性来划分数据集，将会得到很大的信息增益，但是，这样的属性并不一定是最优划分属性。
    (2)ID3算法只能处理离散属性，对于连续性属性，在分类前需要对其离散化。
    (3)ID3算法不能处理属性具有缺失值的样本。
    (4)没有采用剪枝，决策树的结构可能过于复杂，出现过拟合。

        接下来给出第二种可视化方法：

####可视化方法2
#定义文本框和箭头格式
decisionNode = dict(boxstyle='sawtooth', fc='0.8')
leafNode = dict(boxstyle='round4', fc='0.8')
arrow_args = dict(arrowstyle='<-')
#设置中文字体
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
 
def getNumLeafs(myTree):
    numLeafs = 0#初始化叶子
    firstStr = next(iter(myTree))
    secondDict = myTree[firstStr]#获取下一组字典
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':#测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs
 
def getTreeDepth(myTree):
    maxDepth = 0#初始化决策树深度
    #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，
    #可以使用list(myTree.keys())[0]
    firstStr = next(iter(myTree))
    secondDict = myTree[firstStr]#获取下一个字典
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':#测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth#更新层数
    return maxDepth
 
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    arrow_args = dict(arrowstyle="<-")#定义箭头格式
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)#设置中文字体
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',#绘制结点
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, fontproperties=font)
 
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]#计算标注位置
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
 
def plotTree(myTree, parentPt, nodeTxt):
    decisionNode = dict(boxstyle="sawtooth", fc="0.8")#设置结点格式
    leafNode = dict(boxstyle="round4", fc="0.8")#设置叶结点格式
    numLeafs = getNumLeafs(myTree)#获取决策树叶结点数目，决定了树的宽度
    depth = getTreeDepth(myTree)#获取决策树层数
    firstStr = next(iter(myTree))#下个字典
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)#标注有向边属性值
    plotNode(firstStr, cntrPt, parentPt, decisionNode)#绘制结点
    secondDict = myTree[firstStr]#下一个字典，也就是继续绘制子结点
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD#y偏移
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':#测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            plotTree(secondDict[key], cntrPt, str(key))#不是叶结点，递归调用继续绘制
        else: #如果是叶结点，绘制叶结点，并标注有向边属性值
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
 
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)#去掉x、y轴
    plotTree.totalW = float(getNumLeafs(inTree))#获取决策树叶结点数目
    plotTree.totalD = float(getTreeDepth(inTree))#获取决策树层数
    plotTree.xOff = -0.5 / plotTree.totalW
    plotTree.yOff = 1.0#x偏移
    plotTree(inTree, (0.5, 1.0), '')#绘制决策树
    plt.show()
 
if __name__ == '__main__':
    mytree = {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
    createPlot(mytree)