- 1Java数据结构篇之顺序表_数据结构 java排序顺序表
- 2语义分割经典网络(对Web3(Web3.0)受到关注的背景和轻量化模型发展趋势)_webv3
- 3python字符串数据类型_Python基本数据类型之字符串
- 4Redis原理解密:从存储原理到字典的实现_redis存储数据字典
- 5Python的xml模块:处理XML数据的利器_python结合xml
- 6Spring-boot自动装配原理_springboot自动装配原理
- 7Android FileProvider详细解析和10.0的适配_app 开机启动fileprovider
- 8Apple Developer 个人开发者账号申请流程_苹果开发者账号
- 9数据库(表结构)设计技巧及注意事项_表结构设计规范
- 10Android FileProvider特性与Intent重定向漏洞
信号降噪方法
赞
踩
傅里叶变换
只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。“对非平稳过程,傅里叶变换有局限性”。

短时傅里叶变换(Short-time Fourier Transform, STFT)
把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。但是窗函数宽度不好定义。窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。



小波变换
小波是把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。能够获取 频率 和 时频。

基函数会伸缩、会平移(其实本质并非平移,而是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系。那么就知道信号包含该频率的成分的多少。

小波 区别于 傅里叶变换在于,将无限长的三角函数基换成了有限长的会衰减的小波基。小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。
对于突变信号,傅里叶变换存在吉布斯效应,我们用无限长的三角函数怎么也拟合不好突变信号。

小波分解,信号的能量主要分布在低分辨的尺度函数上,而噪声的能量分布不变,仍然均匀分布在所有小波系数上。因此,小波阈值去噪方法就是保留或收缩大的小波系数(低频系数),剔除小的小波系数(高频系数)。在使用小波阈值法对光谱数据进行去噪处理时,选取不同的阈值函数反映了对小波稀疏模的不同处理策略,通常阈值函数米用 Donoho 等在文章“Ideal Spatial Adaptat1n by Wavelet Shrinkage”(B1metrika, Vol.81, N0.3,pp.425-455,1994)提出的硬阈值函数(Hard Threshold Funct1n)和软阈值函数(Soft Threshold Funct1n)两种。其中硬阈值函数对于信号的细节特征可以很好地保留,但在阈值±T处不连续,且不可导,同时其剔除了小于阈值的小波系数,不加处理的完全保留了大于阈值的小波系数,因此重构信号容易产生较大的均方差,出现振荡;软阈值函数在阈值±Τ处是连续的,可以避免去噪后的信号产生振荡现象,但估计的小波系数与实际信号的小波系数之间存在恒定的偏差,使得重构的信号过度平滑,使得边缘相对模糊,同样影响去噪效果。
指数软硬择中阈值降噪
目的:对光谱信号进行去噪处理,以减少了降噪后光谱信号的噪声残留,提高了光谱信号的信噪比。
实现:
步骤1:对输入的含噪光谱信号进行多层小波变换。采用db4小波对含噪光谱信号进行5层分解,分别得到小波的低频系数和高频系数;
步骤2:对步骤I得到的各层高频小波系数进行收缩处理。在收缩处理中阈值函数采用了本发明所提出的指数软硬择中阈值函数,即

(Tj为阈值,ω jk为第j层的小波系数,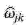 为阈值收缩后的小波系数,j为小波分解的层数,k则表示第k个小波系数。)
为阈值收缩后的小波系数,j为小波分解的层数,k则表示第k个小波系数。)
阈值Tj采用了分层阈值对各层的小波高频系数进行收缩处理,分层阈值为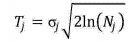 Nj为小波分解第j层小波系数的长度,
Nj为小波分解第j层小波系数的长度,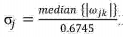 为第j层噪声的标准差,{ωjk}为第j层小波系数。
为第j层噪声的标准差,{ωjk}为第j层小波系数。
步骤3:小波反变换获得小波LOCAL_LDLIBS += -lm
去噪后的信号估计。利用步骤I得到的小波低频系数和步骤2经过小波阈值处理的高频系数进行小波反变换,获得小波分层去噪后的信号估计值。
步骤4:信号中值滤波处理。为了有效去除含噪光谱中的脉冲干扰,对步骤3所得到的信号估计值,进一步进行中值滤波。
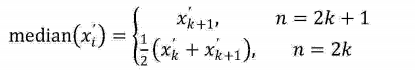
该指数软硬择中阈值函数与传统的阈值函数相比有以下优点:
(1)当|ωjk|≥Tj时,指数软硬择中阈值函数具有高阶导函数;
(2)函数的渐进方程是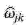 =ωjk,克服了单纯软阈值函数估计出来的
=ωjk,克服了单纯软阈值函数估计出来的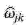 具有恒定偏差Tj(|ωjk|≥Tj)的局限,从而可以更好地、更完整地保留光谱信号的峰值点。
具有恒定偏差Tj(|ωjk|≥Tj)的局限,从而可以更好地、更完整地保留光谱信号的峰值点。
效果评估:
SNR:

MSE:

Extend Empirical Mode Decomposition扩展的经验模态分解
方法的关键是经验模式分解,它能使复杂信号分解为有限个本征模函数(Intrinsic Mode Function,简称IMF),所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。经验模态分解法能使非平稳数据进行平稳化处理,再进行希尔伯特变换获得时频谱图,得到有物理意义的频率。
EMD分解方法
EMD将原始信号分解成本征模态函数(IMF)分量
一个本征模态函数是:
⑴l函数在整个时间范围内,局部极值点和过零点的数目必须相等或最多相差一个;
⑵在任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络(下包络线) 平均必须为零。
EMD分解过程
a.筛选过程就是EMD用于将信号分解成IMF的过程。
b.对于一个信号X(t),从三次样条插值的局地最大值和最小值确定上下包络,让m1表示上下包络的均值。局地性是由任意参数确定;计算时间和EMD的有效性很大程度上取决于这个参数。
c.第一个分量h1计算方法:h1=X(t)-m1
d.在第二个筛选过程中,h1被视作数据,m11是h1的上下包络的均值:h11=h1-m11
e.筛选过程重复k次,直到h1k是一个本征模态函数,即:h1(k-1)-m1k=h1k
f.随后它被指定为c1=h1k,数据中第一个IMF分量,它包含了信号中最短的周期分量。我们将它从数据剩余部分中分离:X(t)-c1 = r1 这个过程重复rj次:r1-c2 = r2,…,rn-1 - cn = rn。
g.结果是一组函数;在集合中函数的数目依赖与原始信号。
EEMD特点
继承了EMD 的自适性; 引入了白噪声扰动并进行集合平均,避免了尺度混合问题, 使得最终分解的IMFs 保持了物理上的唯一性。
EEMD 具体步骤:
1)将待分析的资料数据序列叠加上给定振幅的白噪声序列。
2)将加入白噪声后的数据——混合的信号(原始信号)进行EMD 分解。
3)反复重复这两步骤, 每次加入振幅相同的新生的白噪声序列从而得到不同的 IMFs。
4)最后将各次分解得到的IMFs 求集合平均, 并将其作为最终的分解结果。
这样就得到了各个固有尺度上的IMFs。此外, EMD 除了不能保证每个IMF 都具有很好的物理意义外, 亦不能估计分解得到的IMFs 的信度。但EEMD 可借助于白噪声的集合扰动进行显著性检验, 从而给出各个IMF 的信度。
来源:
zhuanlan.zhihu.com/p/22450818
https://patents.google.com/patent/CN104182946A/
https://www.cnblogs.com/jiangleads/articles/9462087.html


