【LeetCode】动态规划 刷题训练(二)

62. 不同路径

点击查看：不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

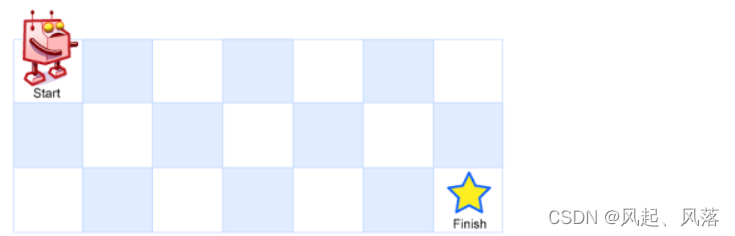
示例 1：
输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

题目解析

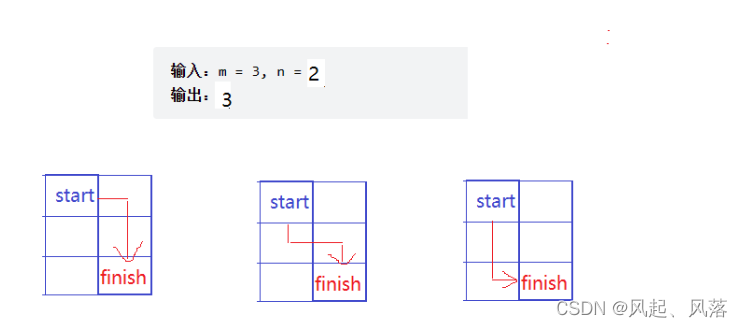
只能向下或者向右走，而且不能回退
所以从start到 finish ，共有三种情况

状态转移方程

dp [i,j ] : 表示走到[i, j ]位置时，共有多少条路径

根据最近的一步，划分问题

---

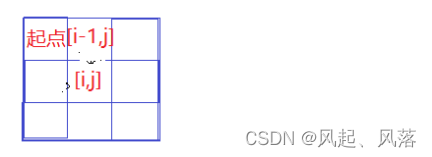
当处于 [i,j]位置时，可以从 [i-1,j] 位置 向下移动得到

从起点位置开始，移动到[i-1,j]位置上，然后再走一步到达[i,j]位置
从[i-1,j] 到[i,j]的总方法数 等于 从起点到 [i-1,j] 的总方法数 即 dp[i-1,j]

---

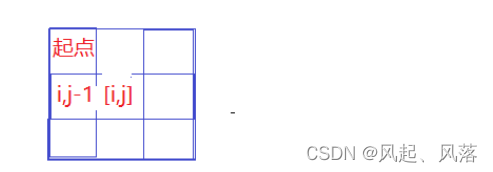
当处于 [i,j]位置时，可以从[i,j-1]位置向右移动得到

从起点位置开始，移动到[i,j-1]位置上，然后再走一步到达[i,j]位置
从[i,j-1] 到[i,j]的总方法数 等于 从起点到 [i,j-1] 的总方法数 即 dp[i,j-1]

---

状态转移方程为：
dp[i][j]= dp[i-1][j] + dp[i][j-1];

完整代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 将 m+1个vector数组 都初始化为 n+1
      vector<vector<int>> dp(m+1,vector<int>(n+1));
       int i=0;
       int j=0;
       //为了防止越界情况，所以扩列 一行和一列，并将其初始化
       dp[0][1]=1;
       for(i=1;i<=m;i++)
       {
           for(j=1;j<=n;j++)
           {
              dp[i][j]=dp[i-1][j]+dp[i][j-1];
           }
       }
       //由于dp是扩列数组，所以下标+1
       return dp[m][n];
    } 
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

---

通过扩列的方式，进行初始化
多扩出一行和一列，相当于虚拟存在的
因为每个[i,j] 的路径总数 都是由 [i-1,j] 和[i,j-1] 位置 相加得来的
所以在 start 的上一个位置处 将其置为1，其他都置为0，
就可以满足原数组的第一行和第一列都为1

63. 不同路径 II

点击查看：不同路径||

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

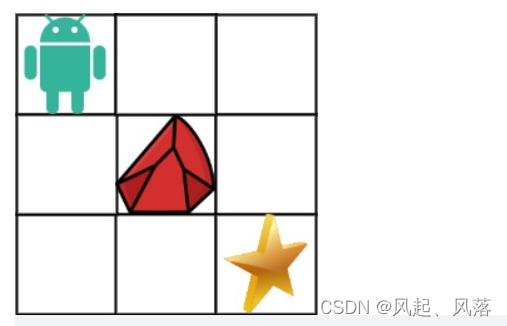
示例 1：
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

题目解析

与不同路径 1 的区别是 加入了 障碍物

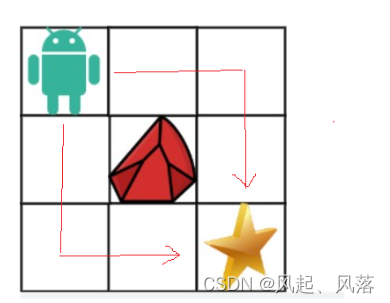
因为中间有障碍物存在，所以只有两种通过方法

状态转移方程

dp[i][j] ：表示 从起点到达 [i,j]位置 共有多少 种 方法

若[i,j]位置作为障碍物，则方案作废，方案数为0

若[i,j]位置没有障碍物，可以从 [i-1,j] 位置 向下 达到 [i,j]位置 ，
从起点位置开始，移动到[i-1,j]位置上，然后再走一步到达[i,j]位置
从[i-1,j] 到[i,j]的总方法数 等于 从起点到 [i-1,j] 的总方法数 即 dp[i-1,j]

若[i,j]位置没有障碍物，也可以 从 [i,j-1] 位置 向右达到 [i,j] 位置
从起点位置开始，移动到[i,j-1]位置上，然后再走一步到达[i,j]位置
从[i,j-1] 到[i,j]的总方法数 等于 从起点到 [i,j-1] 的总方法数 即 dp[i,j-1]

---

状态转移方程为：
dp[i][j] =dp[i-1][j] +dp[i][j-1]; (若[i,j]位置 为 障碍物则为0)

完整代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& ob) {
           int m=ob.size();//行
           int n=ob[0].size();//列

           //将m+1个vector数组 都初始化为n+1
           vector<vector<int>> dp(m+1,vector<int>(n+1));
              
              int i=0;
              int j=0;
              dp[1][0]=1;
              for(i=1;i<=m;i++)
              {
                  for(j=1;j<=n;j++)
                  {
                      //ob作为原数组，映射到扩列后的数组需要行-1 列-1
                      if(ob[i-1][j-1]==0)
                      {
                          //若[i,j]位置不是障碍物
                        dp[i][j]=dp[i-1][j]+dp[i][j-1];
                      }
                  }
              }

              return dp[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

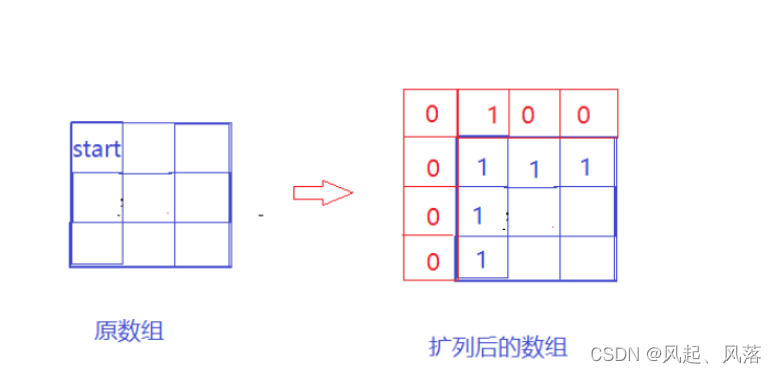
依旧需要创建一个扩列的数组，将起点上一个位置 置为1
使原数组第一行和第一列都为1
因为题中所给的ob数组存在障碍物，所以需要借助ob数组 判断 扩列数组的对应位置
若扩列数组位置为[i,j] ，则ob数组为[i-1,j-1] ，该位置若等于1，则为障碍物，其方案数为0

剑指 Offer 47. 礼物的最大价值

点击查看： 礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

题目解析

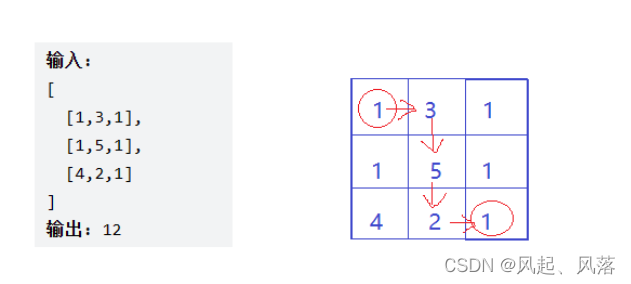
二维数组的每一个元素对应的数，都表示价值，数越大，价值越大
通过向下 或者 向右 寻找 一条 最大价值的 路径
从最上角的1开始，到最下角的1结束

状态转移方程

dp[i][j]：表示 从起点到 [i,j]位置的时候，能拿到 最大价值的礼物

---

dp[i][j] 可以分为两种情况

---

第一种情况 由 [i-1,j] 位置向下走一步得到 [i][j]位置

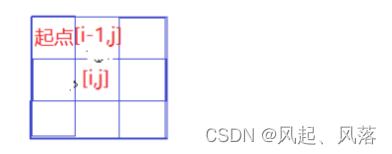
若从起点到[i-1,j]位置 为当前的 最大价值 ，即dp[i-1][j]
则 再加上当前[i,j]位置对应的数 即为 dp[i][j]的价值
dp[i-1,j]+cost[i,j]

---

第二种情况 由 [i,j-1] 位置 向右走一步得到 [i][j]位置

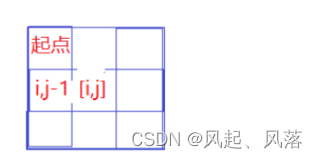
若从起点到[i,j-1]位置 为当前的 最大价值 ，即dp[i][j-1]
则加上当前[i,j]位置对应的数 即为 dp[i][j]的价值
dp[i,j-1]+cost[i,j]

---

将第一种情况的价值与 第二种情况的价值进行比较，取其中大的，则为dp[i][j]的最大价值
dp[i][j]= max(dp[i-1,j]+ cost[i,j] , dp[i,j-1]+ cost[i,j]);

完整代码

class Solution {
public:
    int maxValue(vector<vector<int>>& cost) {
       int m=cost.size();//行
       int n=cost[0].size();//列
       //dp数组 扩列了一行和一列
       vector<vector<int>>dp(m+1,vector<int>(n+1));
       int i=0;
       int j=0;
       for(i=1;i<=m;i++)
       {
           for(j=1;j<=n;j++)
           {
         //cost作为原数组，而dp作为扩列数组，cost想要使用dp数组中的下标，需要减一行减一列
               dp[i][j]=max(dp[i-1][j]+cost[i-1][j-1],dp[i][j-1]+cost[i-1][j-1]);
           }
       }
       //由于是扩列数组，所以返回下标m和n的位置
       return dp[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

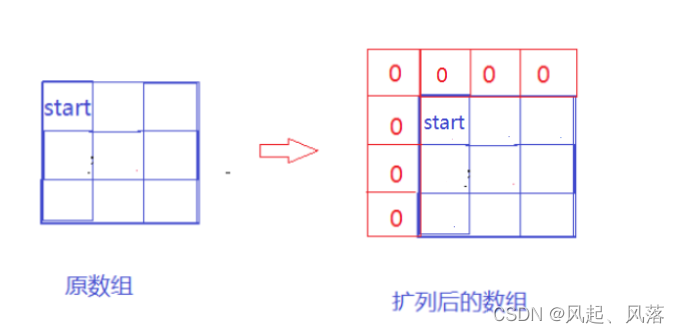
对于dp数组 start 的位置处，根据状态转移方程，
该位置的最大价值是由 上一个位置以及左一个位置的最大值加上该位置的值 得到的，
但此时 上一个位置以及左一个位置 都是虚拟的，所以理应都设置为0

---

由于cost数组 是原数组，而dp数组作为扩列数组，cost数组想要dp数组的下标，就需要减一行以及减一列