花生_TL007

这个屌丝很懒，什么也没留下！

热门标签

特征工程——数据的标准化（Z-Score,Maxmin,MaxAbs,RobustScaler,Normalizer）

作者：花生_TL007 | 2024-03-30 12:59:28

踩

z-score标准化

数据标准化是一个常用的数据预处理操作，目的是处理不同规模和量纲的数据，使其缩放到相同的数据区间和范围，以减少规模、特征、分布差异等对模型的影响。

比如线性回归模型、逻辑回归模型或包含矩阵的模型，它们会受到输入尺度(量纲)的影响。相反，那些基于树的模型则根本不在乎输入尺度(量纲)有多大。如果模型对输入特征的尺度(量纲)很敏感，就需要进行特征缩放。顾名思义，特征缩放会改变特征的尺度，有些人将其称为特征归一化。特征缩放通常对每个特征独立进行。下面讨论几种常用的特征缩放操作，每种操作都会产生一种不同的特征值分布。

标准化方法	公式	优点	缺点	转换区间	适用场景
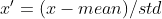
Z-Score(标准化standardization)		适用大多数类型的数据，标准化之后的数据是以0为均值，方差为1的正态分布	是一种中心化方法，会改变原有数据得分布结构	均值为0，方差为1的标准正态分布	不适合用于稀疏数据的处理
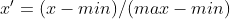
Max-Min(归一化)		应用广泛，能较好的保持原有数据分布结构	1.分母可能为0，导致计算过程出错。 2.对异常值(离群值)的存在非常敏感	[0,1]	不适合用于稀疏数据的处理
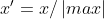
MaxAbs	${x}'=x/\left \| max \right \|$	保持原有数据分布结构	对异常值(离群值)的存在非常敏感	[-1,1]	稀疏数据、稀疏CSR或CSC矩阵
RobustScaler	，Q代表分位数	能最大限度地保留数据集中的异常(离群点)	-	-	最大限度保留数据集中的异常(离群值)
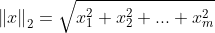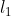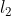
Normalizer(正则化Normalization)	对每个样本计算其范数 $\left \\| x \right \\|_{2}=\sqrt{x^{2}_{1}+x^{2}_{2}+...+x^{2}_{m}}$ ，然后该样本中每个元素进行除以该范数 $\tilde{x}=\frac{x}{\left \\| x \right \\|_{2}}$ (即将每一个样本点看成一个向量，将其规范化成单位向量)	一个单向量上来实现这正则化的功能。正则化有 $l_{1}$ , $l_{2}$	-	-	经常被使用在分类与聚类中。

注：

1、稀疏数据集：存在稀疏性特征，特征表现为标准差小，并有很多元素的值为0，最常见的稀疏数据集是用来做协同过滤的数据集。

2、CSR(Compressed Spare Row，行压缩)和CSC(Compressed Spare Column，列压缩)是稀疏矩阵的两种存储格式，这两种稀疏矩阵在scipy.sparse包中应用广泛。

一、sklearn代码实现及相关原理

1、Z-Score(标准化)


import numpy as np
 
import matplotlib.pyplot as plt
 
from sklearn import preprocessing
 
data=np.array([[1,2,3],[4,5,6],[7,8,9]])
 
data
 
 
 
#Z-score标准化
 
zscore_scaler=preprocessing.StandardScaler()
 
data_zcore_1=zscore_scaler.fit_transform(data)
 
data_zcore_1
 
 
 
 
 
#算法原理
 
data_zcore_2=(data-data.mean(axis=0))/data.std(axis=0)
 
data_zcore_2

输出：


 
array([[1, 2, 3],
 
[4, 5, 6],
 
[7, 8, 9]])
 
 
 
array([[-1.22474487, -1.22474487, -1.22474487],
 
[ 0. , 0. , 0. ],
 
[ 1.22474487, 1.22474487, 1.22474487]])
 
 
 
array([[-1.22474487, -1.22474487, -1.22474487],
 
[ 0. , 0. , 0. ],
 
[ 1.22474487, 1.22474487, 1.22474487]])

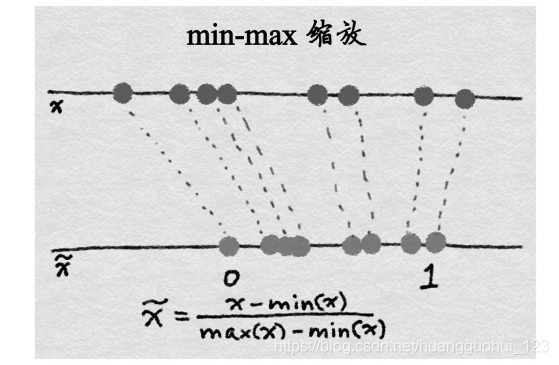
2、Max-Min(归一化)


import numpy as np
 
import matplotlib.pyplot as plt
 
from sklearn import preprocessing
 
data=np.array([[1,2,3],[4,5,6],[7,8,9]])
 
data
 
 
 
#Max-Min标准化
 
minmax_scaler=preprocessing.MinMaxScaler()
 
data_minmax_1=minmax_scaler.fit_transform(data)
 
data_minmax_1
 
 
 
#算法原理
 
data_minmax_2=(data-data.min(axis=0))/(data.max(axis=0)-data.min(axis=0))
 
data_minmax_2

输出：


 
array([[1, 2, 3],
 
[4, 5, 6],
 
[7, 8, 9]])
 
 
 
array([[0. , 0. , 0. ],
 
[0.5, 0.5, 0.5],
 
[1. , 1. , 1. ]])
 
 
 
array([[0. , 0. , 0. ],
 
[0.5, 0.5, 0.5],
 
[1. , 1. , 1. ]])

【注意】：不要“中心化”稀疏数据！

在稀疏特征上执行min-max缩放和标准化时一定要慎重，它们都会从原始特征值中减去一个量。对于min-max缩放，这个平移量是当前特征所有值中的最小值；对于标准化，这个量是均值。如果平移量不是0，那么这两种变换会将一个多数元素为0的稀疏特征向量变成密集特征向量。根据实现方式的不同，这种改变会给分类器带来巨大的计算负担。

3、MaxAbs


import numpy as np
 
import matplotlib.pyplot as plt
 
from sklearn import preprocessing
 
data=np.array([[1,2,3],[4,5,6],[7,8,9]])
 
data
 
 
 
#MaxAbsScaler标准化
 
maxabs_scaler=preprocessing.MaxAbsScaler()
 
data_maxabs_1=maxabs_scaler.fit_transform(data)
 
data_maxabs_1
 
 
 
#算法原理
 
data_maxabs_2=data/np.abs(data.max(axis=0))
 
data_maxabs_2

输出：


array([[1, 2, 3],
 
[4, 5, 6],
 
[7, 8, 9]])
 
 
 
array([[0.14285714, 0.25 , 0.33333333],
 
[0.57142857, 0.625 , 0.66666667],
 
[1. , 1. , 1. ]])
 
 
 
array([[0.14285714, 0.25 , 0.33333333],
 
[0.57142857, 0.625 , 0.66666667],
 
[1. , 1. , 1. ]])

4、RobustScaler


import numpy as np
 
import matplotlib.pyplot as plt
 
from sklearn import preprocessing
 
data=np.array([[1,2,3],[4,5,6],[7,8,9]])
 
data
 
 
 
#RobustScaler标准化
 
Robust_scaler=preprocessing.RobustScaler()
 
data_Robust_1=Robust_scaler.fit_transform(data)
 
data_Robust_1
 
 
 
#算法原理
 
data_Robust_2=(data-np.nanmedian(data,axis=0))/(np.percentile(data,75,axis=0)-np.percentile(data,25,axis=0))
 
data_Robust_2

输出：


array([[1, 2, 3],
 
[4, 5, 6],
 
[7, 8, 9]])
 
 
 
array([[-1., -1., -1.],
 
[ 0., 0., 0.],
 
[ 1., 1., 1.]])
 
 
 
array([[-1., -1., -1.],
 
[ 0., 0., 0.],
 
[ 1., 1., 1.]])

5、Normalizer(正则化/归一化)

正则化可以理解为将行(样本点)看成一个向量，将向量规范化成单位向量。

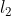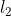这种归一化技术是将初始特征值除以一个称为 $l_{2}$ 范数的量， $l_{2}$ 范数又称为欧几里得范数，它的定义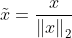： $\tilde{x}=\frac{x}{\left \| x \right \|_{2}}$

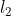$l_{2}$ 范数是坐标空间中向量长度的一种测量。它的定义可以根据著名的毕达哥拉斯定理(给定一个直角三角形两条直角边的长度，可以求出斜边的长度)导出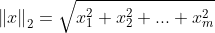： $\left \| x \right \|_{2}=\sqrt{x^{2}_{1}+x^{2}_{2}+...+x^{2}_{m}}$

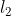$l_{2}$ 范数先对所有数据点中该特征的值的平方求和，然后算出平方根。经过 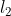$l_{2}$ 归一化后，特征列的范数就是1。有时候这种处理又称为 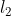$l_{2}$ 缩放。(不严格地说，缩放意味着乘以一个常数，而归一化可以包括多种操作)。下图演示了 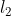$l_{2}$ 归一化的过程。

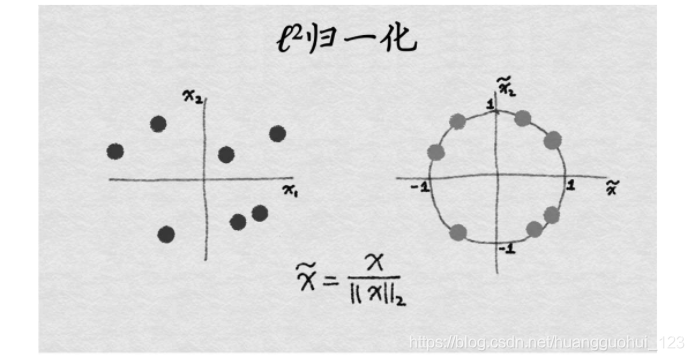
5.1、正则化的应用场景

有三个人的身高、臂展的二维数据，数据分布情况如下(向量表示)：

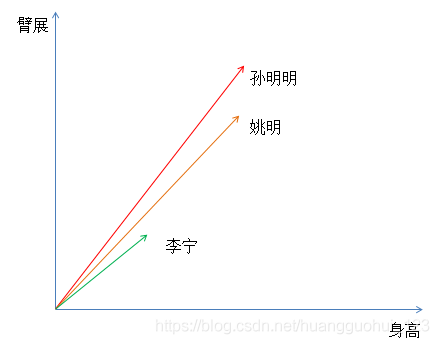
如果光从上面的数据聚类，我们可能将姚明和孙明明聚成一类，李宁单独一类。

但是我们后来知道，孙明明没有进NBA的原因是他是巨人症患者(巨人症患者的突出特点是臂展要比身高还长) ，普通人一般身高和臂展差不多，姚明的身高为2.20m，臂展为2.10m，但是孙明明的身高为2.30m，臂展达到2.50m。所以从某种意义上我们应该将孙明明聚成一类(巨人症)，姚明和李宁聚成一类(非巨人症)。

这个时候我们可以对上图的向量进行正则化Normalizer，经过正则化的向量为单位向量，方向与原向量是不变的。如下图：

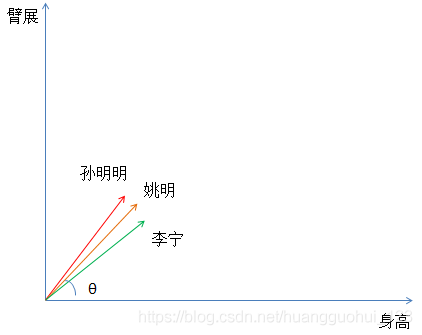
经过正则化，我们比较的不再是身高和臂展的数值化的差异，而是臂展和升高的比率(即角度θ)。大于1即为巨人症，小于等于1即为普通人，这个时候就容易将孙明明单独聚成一类。

从以上的场景可以看出：正则化适用的场景为，如果数据集之间各个指标有一个比率的关系，而且比率关系比各指标的绝对值更重要的时候，用Normalizer(正则化)可以达到一个比较好的效果。

对鸢尾花(Irises)数据集的聚类，就适用于此场景。


import numpy as np
 
import matplotlib.pyplot as plt
 
from sklearn import preprocessing
 
data=np.array([[1,2,3],[4,5,6],[7,8,9]])
 
data
 
## 正则化
 
Normal_scaler=preprocessing.Normalizer()
 
data_Normal_1=Normal_scaler.fit_transform(data)
 
data_Normal_1
 
## 算法原理
 
data_Normal_2=np.divide(data,((data**2).sum(axis=1)**0.5).reshape(3,1))
 
data_Normal_2

输出：


array([[1, 2, 3],
 
[4, 5, 6],
 
[7, 8, 9]])
 
 
 
array([[0.26726124, 0.53452248, 0.80178373],
 
[0.45584231, 0.56980288, 0.68376346],
 
[0.50257071, 0.57436653, 0.64616234]])
 
 
 
array([[0.26726124, 0.53452248, 0.80178373],
 
[0.45584231, 0.56980288, 0.68376346],
 
[0.50257071, 0.57436653, 0.64616234]])

二、案例说明

不论使用何种缩放方法，特征缩放总是将特征除以一个常数。因此，它不会改变单特征分布的形状。我们使用在线新闻文章单词数量来说明这一点。

1、读取数据


import pandas as pd
 
import sklearn.preprocessing as preproc
 
 
 
df = pd.read_csv('D:/高济医疗/精通特征工程/精通特征工程/data/OnlineNewsPopularity.csv', delimiter=', ')
 
 
 
# 原始数据-文章中单词数量
 
df['n_tokens_content']

输出：


 
0 219.0
 
1 255.0
 
2 211.0
 
3 531.0
 
4 1072.0
 
...
 
39639 346.0
 
39640 328.0
 
39641 442.0
 
39642 682.0
 
39643 157.0
 
Name: n_tokens_content, Length: 39644, dtype: float64

2、数据标准化


# Min-max scaling
 
df['minmax'] = preproc.minmax_scale(df[['n_tokens_content']])
 
 
 
# Standardization
 
df['standardized'] = preproc.StandardScaler().fit_transform(df[['n_tokens_content']])
 
 
 
#MaxAbs
 
df['maxabs'] = preproc.maxabs_scale(df[['n_tokens_content']], axis=0)
 
 
 
#RobustScaler
 
df['Robust'] = preproc.RobustScaler().fit_transform(df[['n_tokens_content']])
 
 
 
# L2-normalization
 
df['l2_normalized'] = preproc.normalize(df[['n_tokens_content']], axis=0)

3、数据可视化


fig, (ax1, ax2, ax3, ax4,ax5, ax6) = plt.subplots(6,1,figsize=(10,9))
 
fig.tight_layout(pad=0, w_pad=1.0, h_pad=2.0)
 
 
 
df['n_tokens_content'].hist(ax=ax1, bins=100)
 
ax1.tick_params(labelsize=14)
 
ax1.set_xlabel('Article word count', fontsize=14)
 
 
 
df['minmax'].hist(ax=ax2, bins=100)
 
ax2.tick_params(labelsize=14)
 
ax2.set_xlabel('Min-max scaled word count', fontsize=14)
 
 
 
df['standardized'].hist(ax=ax3, bins=100)
 
ax3.tick_params(labelsize=14)
 
ax3.set_xlabel('Standardized word count', fontsize=14)
 
ax3.set_ylabel('Number of articles', fontsize=14)
 
 
 
df['maxabs'].hist(ax=ax4, bins=100)
 
ax4.tick_params(labelsize=14)
 
ax4.set_xlabel('Maxabs word count', fontsize=14)
 
 
 
df['Robust'].hist(ax=ax5, bins=100)
 
ax5.tick_params(labelsize=14)
 
ax5.set_xlabel('Robust word count', fontsize=14)
 
 
 
df['l2_normalized'].hist(ax=ax6, bins=100)
 
ax6.tick_params(labelsize=14)
 
ax6.set_xlabel('L2-normalized word count', fontsize=14)

输出：

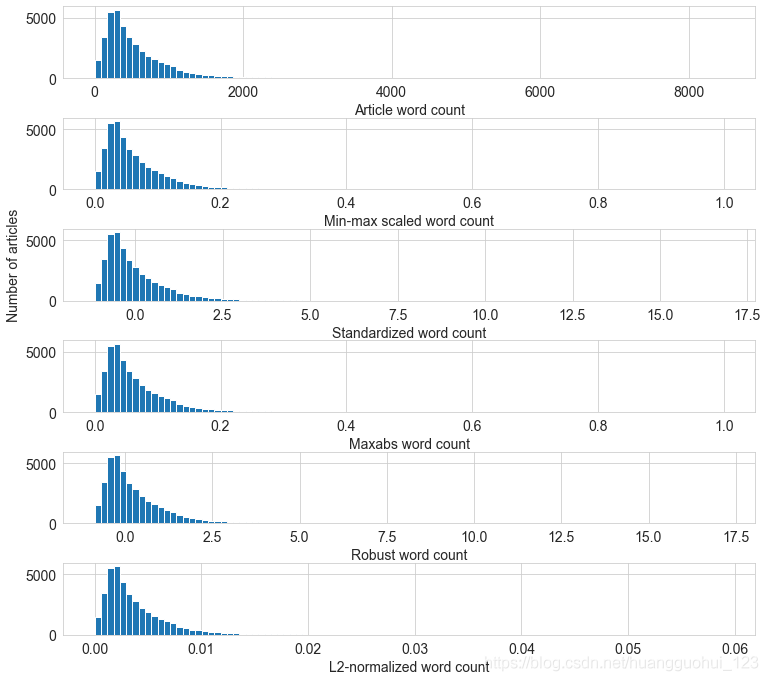
从图中可以看出：与对数变换(《机器学习——特征工程——对数转换、Box-Cox转换》)不同，注意只有x轴的尺度发生了变化，特征缩放后的分布形状保持不变。

总结：当一组输入特征的尺度相差很大时，就需要进行特征缩放。例如，一个人气很高的商业网站的日访问量可能是几十万次，而实际购买行为可能只有几千次。如果这两个特征都被模型所使用，那么模型就需要在确定如何使用它们时先平衡一下尺度。如果输入特征的尺度差别非常大，就会对模型训练算法带来数值稳定性方面的问题。在这种情况下，就应该对特征进行标准化。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/340766