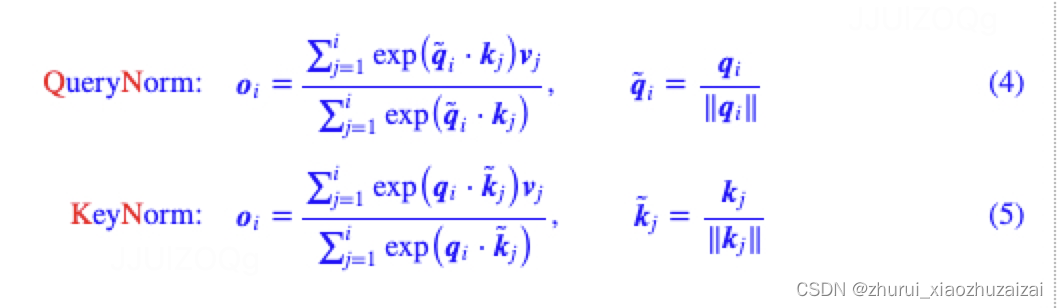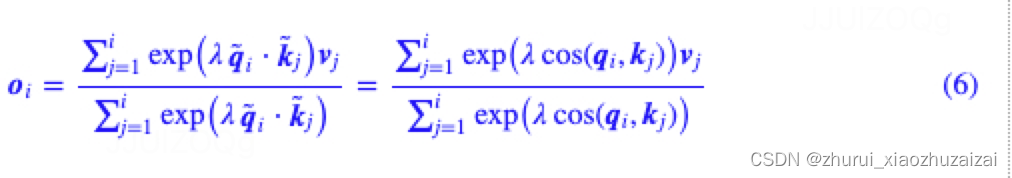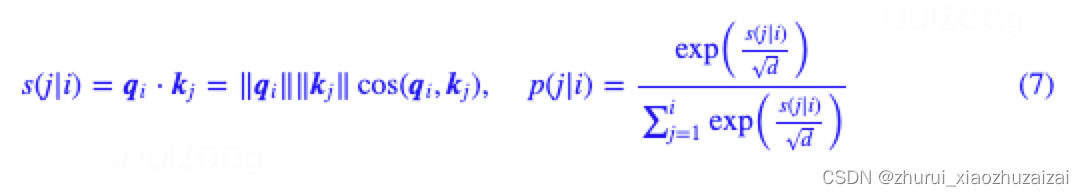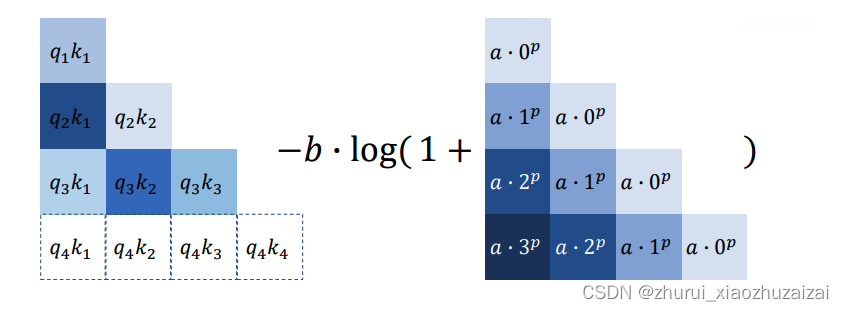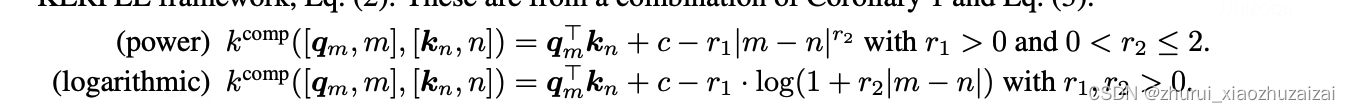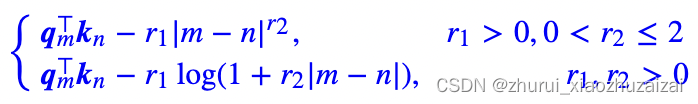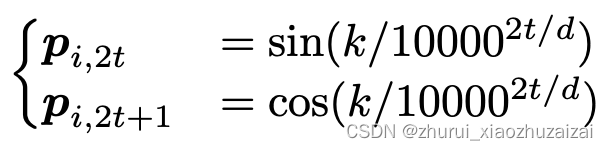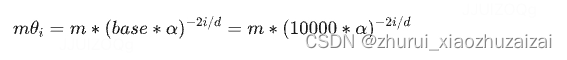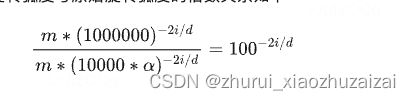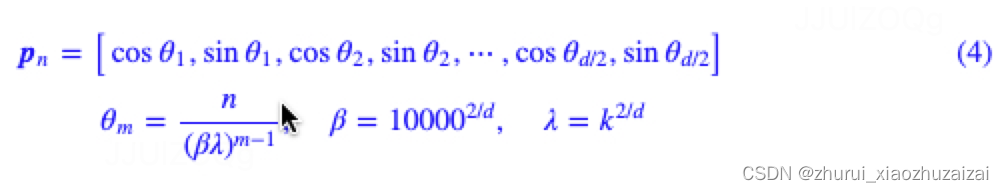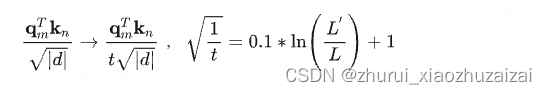位置编码与外推性[bias(Alibi/KERPLE/Sandwich)+插值 + ROPE/RERope + keynorm。与长度外推性]_alibi位置编码

Transformer升级之路：7、长度外推性与局部注意力
Transformer升级之路：8、长度外推性与位置鲁棒性
Bias项的神奇作用：RoPE + Bias = 更好的长度外推性

长度外推

1.1 什么是长度外推性？

长度外推性=train short, test long
train short：1）受限于训练成本；2）大部分文本的长度不会特别长，训练时的max_length特别特别大其实意义不大（长尾）。
test long：这里long是指比训练时的max_length长，希望不用微调就能在长文本上也有不错的效果。

1.2 为了做到长度外推性，需要解决两个主要问题：

1）预测时位置编码的外推：没见过的就无法保证很好的泛化，不仅学习式位置编码如此；像正弦位置编码、RoPE也有这样的问题，它们自身虽然不用学习，但是会影响上层参数的学习；
2）预测时序列更长，导致注意力相比训练时更分散：序列长度增大意味着attention分布的熵增大了，注意力更分散了；

1.3 长度外推性的推测

可见，长度外推性问题并不完全与设计一个良好的位置编码等价。
然后，还有个问题是，虽然PE一直是transformer类模型中的重要的基础组件，很多位置编码也在尝试做一些外推性的工作，但整体来看早期的LLM其实没有特别关注或者说纠结长度外推性，直到后面各种NLG模型的崛起，尤其是ChatGPT的出现，大家才惊觉原来上下文可以做的这么长了？

为什么目前市面上的LLM鲜有使用呢（据目前所知，好像只有BLOOM/MPT/采用了ALiBi）？可能的原因：

1）专注于长度外推性的工作主要是在21/22年后才逐渐出现，效果尚未经过充分检验；
2）长度外推性的评测指标与LLM的评测指标并不完全match：目前长度外推性主要看PPL，这其实不够全面。PPL这类语言模型的指标，可能更关注局部上下文的预测，因此局部注意力相关的方案可能在这类评测上天然占优。
3）目前的长度外推性工作似乎更多的在强调外推性如何如何，但更重要的应该还是max_length内的效果，从LLM的角度来看，应该在保证max_length内的效果后再去追求外推性。比如，从GLM的消融实验来看，ALiBi的效果还是不如RoPE的。

一直的误解

第一篇明确研究Transformer长度外推性的工作应该是ALIBI，出自2021年中期，距今也不算太久。为什么这么晚（相比Transformer首次发表的2017年）才有人专门做这个课题呢？估计是因为我们长期以来，都想当然地认为Transformer的长度外推性是位置编码的问题，找到更好的位置编码就行了。
事实上，通过对比现有的一些位置编码的外推效果，确实能找到支撑该观点的一些论据。比如后面分享的多篇实验效果显示，相对位置编码的长度外推性，平均好于绝对位置编码的；像RoPE这样的函数式相对位置编码，又会比训练式相对位置编码的外推效果好些。所以看上去，似乎只要我们不断优化位置编码形式，最终就能给Transformer提供更好的长度外推性，从而解决这个问题。然而，情况没有那么乐观，像RoPE算是外推能力较好的位置编码，也只能外推10%到20%左右的长度而保持效果不变差，再长效果就会骤降。这个比例与预期差太远了，设想中好歹能外推个几倍长度才算是有价值的外推，所以不难想象，单靠改进位置编码改进Transformer的长度外推性，就不知道要等多久才能实现更长的效果了。
在直觉上，相信很多读者觉得像Sinusoidal或RoPE之类的函数式位置编码，它们没有训练参数，长度外推性应该很好才对，但事实上并非如此，这类位置编码并没有在长度外推方面表现出什么优势。为什么会这样呢？其实是大家在假设函数式位置编码的外推性时，忘了它的基本前提——“光滑性”。
其实，外推性就是局部推断整体，对此我们应该并不陌生，泰勒级数近似就是经典的例子，它只需要知道函数某点处若干阶导数的值，就可以对一个邻域内的值做有效估计，它依赖的就是给定函数的高阶光滑性（高阶导数存在且有界）。但是Sinusoidal或RoPE是这种函数吗？并不是。它们是一系列正余弦函数的组合，其相位函数是k/100002i/d，当2i/d≈0时，函数近似就是sink,cosk，这算是关于位置编码k的高频振荡函数了，而不是直线或者渐近趋于直线之类的函数，所以基于它的模型往往外推行为难以预估。能否设计不振荡的位置编码？很难，位置编码函数如果不振荡，那么往往缺乏足够的容量去编码足够多的位置信息，也就是某种意义上来说，位置编码函数的复杂性本身也是编码位置的要求。

1.4 实现长度外推性的超强基线

长度外推性是一个训练和预测的长度不一致的问题。具体来说，不一致的地方有两点：

1、预测的时候用到了没训练过的位置编码（不管绝对还是相对）；
2、预测的时候注意力机制所处理的token数量远超训练时的数量。

第1点可能大家都容易理解，没训练过的就没法保证能处理好，这是DL中很现实的现象，哪怕是Sinusoidal或RoPE这种函数式位置编码也是如此。
关于第2点，可能读者会有些迷惑，Attention理论上不就是可以处理任意长度的序列吗？训练和预测长度不一致影响什么呢？答案是熵，我们在《从熵不变性看Attention的Scale操作》也已经分析过这个问题，越多的token去平均注意力，意味着最后的分布相对来说越“均匀”（熵更大），即注意力越分散；而训练长度短，则意味着注意力的熵更低，注意力越集中，这也是一种训练和预测的差异性，也会影响效果。

事实上，对于相对位置编码的Transformer模型，通过一个非常简单的Attention Mask，就可以一次性解决以上两个问题，并且取得接近SOTA的效果：
不难理解，这就是将预测时的Attention变为一个局部Attention，每个token只能看到训练长度个token。这样一来，每个token可以看到的token数跟训练时一致，这就解决了第2个问题，同时由于是相对位置编码，位置的计数以当前token为原点，因此这样的局部Attention也不会比训练时使用更多的未知编码，这就解决了第1个问题。所以，就这个简单的Attention Mask一次性解决了长度外推的2个难点，还不用重新训练模型，更令人惊叹的是，各种实验结果显示，如果以它为baseline，那么各种同类工作的相对提升就弱得可怜了，也就是它本身已经很接近SOTA了，可谓是又快又好的“超强基线”。

对于第二点：

其中m是训练长度，n是预测长度。经过这样修改（下面简称为“logn缩放注意力”），注意力的熵随着长度的变化更加平稳，缓解了这个不一致问题。个人的实验结果显示，至少在MLM任务上，“logn缩放注意力”的长度外推表现更好。

第1点不一致性，即“预测的时候用到了没训练过的位置编码”，那么为了解决它，就应该做到“训练阶段把预测所用的位置编码也训练一下”。一篇ACL22还在匿名评审的论文《Randomized Positional Encodings Boost Length Generalization of Transformers》首次从这个角度考虑了该问题，并且提出了解决方案。
论文的思路很简单：

随机位置训练 设N为训练长度（论文N=40），M为预测长度（论文M=500），那么选定一个较大L>M（这是一个超参，论文L=2048），训练阶段原本长度为N的序列对应的位置序列是[0,1,⋯,N−2,N−1]，现在改为从{0,1,⋯,L−2,L−1}中随机不重复地选N个并从小到大排列，作为当前序列的位置序列。

预测阶段，也可以同样的方式随机采样位置序列，也可以直接在区间中均匀取点（个人的实验效果显示均匀取点的效果一般好些），这就解决了预测阶段的位置编码没有被训练过的问题。不难理解，这是一个很朴素的训练技巧（下面称之为“随机位置训练”），目标是希望Transformer能对位置的选择更加鲁棒一些，但后面我们将看到，它能取得长度外推效果的明显提升。笔者也在MLM任务上做了实验，结果显示在MLM上也是有效果的，并且配合“logn缩放注意力”提升幅度更明显（原论文没有“logn缩放注意力”这一步）。

1.5 长度外推性的新基准

Google去年在论文《Neural Networks and the Chomsky Hierarchy》专门提出的一个长度外泛化基准（下面简称该测试基准为“CHE基准”，即“Chomsky Hierarchy Evaluation Benchmark”），这给我们提供了理解长度外推的一个新视角。

这个基准包含多个任务，分为R（Regular）、DCF（Deterministic Context-Free）、CS（Context-Sensitive）三个级别，每个级别的难度依次递增，每个任务的简介如下：

• Even Pairs，难度R，给定二元序列，如“aabba”，判断2-gram中ab和ba的总数是否为偶数，该例子中2-gram有aa、ab、bb、ba，其中ab和ba共有2个，即输出“是”，该题也等价于判断二元序列的首尾字符是否相同。
• Modular Arithmetic (Simple)，难度R，计算由{0,1,2,3,4}五个数和{+,−,×}三个运算符组成的算式的数值，并输出模5后的结果，比如输入1+2−4，那么等于−1，模5后等于4，所以输出4。
• Parity Check，难度R，给定二元序列，如“aaabba”，判断b的数目是否为偶数，该例子中b的数目为2，那么输出“是”。
• Cycle Navigation，难度R，给定三元序列，其中每个元分别代表+0、+1、−1之一，输出从0出发该序列最终的运算结果模5的值，比如0,1,2分别代表+0,+1,−1，那么010211代表0+0+1+0−1+1+1=2，模5后输出2。
• Modular Arithmetic，难度DCF，计算由{0,1,2,3,4}五个数、括号(,)和{+,−,×}三个运算符组成的算式的数值，并输出模5后的结果，比如输入−(1−2)×(4−3×(−2))，那么结果为10，模5后等于0，所以输出0，相比Simple版本，该任务多了“括号”，使得运算上更为复杂。
• Reverse String，难度DCF，给定二元序列，如“aabba”，输出其反转序列，该例子中应该输出“abbaa”。
• Solve Equation，难度DCF，给定由{0,1,2,3,4}五个数、括号(,)、{+,−,×}三个运算符和未知数z组成的方程，求解未知数z的数值，使得它在模5之下成立。比如−(1−2)×(4−z×(−2))=0，那么z=3，解方程虽然看上去更难，但由于方程的构造是在Modular Arithmetic的基础上将等式中的某个数替换为z，所以保证有解并且解在{0,1,2,3,4}，因此理论上我们可以通过枚举结合Modular Arithmetic来求解，因此它的难度跟Modular Arithmetic相当。
• Stack Manipulation，难度DCF，给定二元序列，如“abbaa”，以及由“POP/PUSH a/PUSH b”三个动作组成的堆栈操作序列，如“POP / PUSH a / POP”，输出最后的堆栈结果，该例子中应该输出“abba”。
• Binary Addition，难度CS，给定两个二进制数，输出它们的和的二进制表示，如输入10010和101，输出10111，注意，这需要都在字符层面而不是数值层面输入到模型中进行训练和预测，并且两个数字是串行而不是并行对齐地提供的（可以理解为输入的是字符串10010+101）。
• Binary Multiplication，难度CS，给定两个二进制数，输出它们的和的二进制表示，如输入100和10110，输出1011000，同Binary Addition一样，这需要都在字符层面而不是数值层面输入到模型中进行训练和预测，并且两个数字是串行而不是并行对齐地提供的（可以理解为输入的是字符串100×10110）。
• Compute Sqrt，难度CS，给定一个二进制数，输出它的平方根的下取整的二进制表示，如输入101001，那么输出结果为⌊101001‾‾‾‾‾‾‾√⌋=101，这个难度同Binary Multiplication，因为至少我们可以从0到所给数结合Binary Multiplication逐一枚举来确定结果。
• Duplicate String，难度CS，给定一个二元序列，如“abaab”，输出重复一次后的序列，该例子应该输出“abaababaab”，这个简单的任务看上去是难度R，但实际上是CS，大家可以想想为什么。
• Missing Duplicate，难度CS，给定一个带有缺失值的二元序列，如“ab_aba”，并且已知原始的完整序列是一个重复序列（上一个任务的Duplicate String），预测确实值，该例子应该输出a。
• Odds First，难度CS，给定一个二元序列t1t2t3⋯tn，输出t1t3t5⋯t2t4t6⋯，如输入aaabaa，将输出aaaaba。
• Bucket Sort，难度CS，给定一个n元数值序列（数列中的每个数都是给定的n个数之一），返回其从小到大排序后的序列，如输入421302214应该输出011222344。

可以看到，这些任务都具有一个共同特点，就是它们的运算都有固定的简单规则，并且理论上输入都是不限长度的，那么我们可以通过短序列来训练，然后测试在短序列上的训练结果能否推广到长序列中。也就是说，它可以作为长度外推性的一个很强的测试基准。

1.6 长度外推性方法分类

我们可以将目前Transformer的长度外推技术分为两类：

一类是事后修改，这类方法的特点是直接修改推理模型，无需微调就能达到一定的长度外推效果，但缺点是它们都无法保持模型在训练长度内的恒等性；
比如NTK-RoPE、YaRN、ReRoPE,KeyNorm等，

另一类自然是事前修改，它们可以不加改动地实现一定的长度外推，但相应的改动需要在训练之前就引入，因此无法不微调地用于现成模型，并且这类方法是否能够Scale Up还没得到广泛认可。
如ALIBI、KERPLE、XPOS以及HWFA等

2 长度外推性与bias和key-norm

2.1 bias与外推性

来自文章：Bias项的神奇作用：RoPE + Bias = 更好的长度外推性

== 结论：Bias项能增强RoPE模型的长度外推性 ==

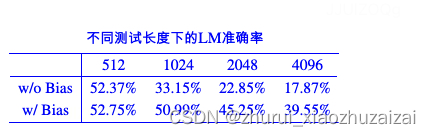
Bias项（偏置项），目前的主流观点是当模型足够大时，Bias项不会有什么特别的作用，所以很多模型选择去掉Bias项，其中代表是Google的T5和PaLM，RoFormerV2和GAU-α也沿用了这个做法。

经过作者实验，Bias项确实不怎么影响训练效果（512长度），但却在长度外推性上面明显拉开了差距，看似毫无存在感的Bias项居然有此神奇作用！当然，要是重跑几次实验，外推性的结果可能会有明显的波动，毕竟长度外推性属于“赠送功能”，并不是我们主动触发的

这时候问题就来了：之前做长度外推性的工作不是都验证了RoPE的外推性不大好了吗？难道它们都没加Bias？为此，笔者特意去考证了一下，果然”不出所料”：
“开山之作”ALIBI和最近的XPOS都是没有加Bias项的，而KERPLE和Sandwich则是加了Bias项的。之前笔者在读论文的时候，就一直感觉KERPLE和Sandwich中的RoPE外推效果似乎比ALIBI和XPOS中的好，现在可以肯定这应该不是错觉了，既然KERPLE和Sandwich都加了Bias，那么根据本文的结论，RoPE是可能呈现出更好的长度外推性的。

为什么有的 Vision Transformer 中的 key 不需要 bias ？，
事实上，“可以去掉Key的Bias”这个结论，是针对没有RoPE的Attention的，由于Softmax的存在，加上的bias可以约掉：
然而，这个“可以约掉”依赖于b跟n无关，

但从伤式我们就知道，经过RoPE后，b也算是m,n的函数了，实际上是无法约掉的，因此对于加了RoPE的模型，Bias项去掉前后会有不一样的效果。

2.2 key-norm与外推性

2.2.1 三种不同的norm

标准的推导是在“qi,kj均独立地采样自“均值为0、方差为1”的分布”的假设下进行的

Scale因子√(1/d)
这个意味着，在Attention的初始阶段两个变体QueryNorm与KeyNorm有着相同的效果：
因此，就有了验证这两个变体与标准的哪个更优的想法。为了描述的方便，我们可以相应地称为“Query/Key-Normalized Dot-Product Attention”，分别简称为“QNA”和“KNA”。

此外，既然可以QueryNorm和KeyNorm，那么自然也可以考虑两者都Norm一下，所以我们将如下“Scaled Cosine Attention（CosA）”也一并进行实验：

即λ=4logn（原文是3.5，但下面训练长度比较小，改为4更精准一些），其中n固定为训练长度的一半，或者动态取位置id加1。

2.2.2 实验结果

1、不管是QueryNorm还是KeyNorm，都在训练长度上取得了更好的效果，虽然这个优势非常微弱，大概率随着训练的进一步推进可以忽略不计，但这个优势非常稳定，暗示着让训练更加平稳的可能性；2、KeyNorm对长度外推的提升非常明显，这就是实验结果中的“意外之喜”！
KeyNorm依然有着无法有效识别超出训练长度的位置（所以“重复”的结果不高）的问题，但有效地避免了PPL爆炸问题（所以“不重复”的结果还不错）。
这对做Long Context的同学来说可能是个好消息：一方面，KeyNorm不像ALIBI、KERPLE等，它的长度外推不用加Local约束，训练完成后也不做任何修改，纯属是“免费的午餐”，甚至看上去加了KeyNorm后训练效果都变好了；另一方面，也因为它是非Local的，所以可以更长文本继续训练，并且继续训练时再也不用纠结是选PI还是ABF了，对于KeyNorm来说，啥也不改就行。

2.2.3 分析

根据标准attention，第i个token与第j个token的相关性打分由内积完成：

第二个等号，我们从几何意义出发，将它分解为了各自模长与夹角余弦的乘积。
注意力p(j|i)是一个条件概率，
‖qi‖只跟当前位置i有关，它不改变注意力的相对大小，而只改变稀疏程度；
‖kj‖则有能力改变p(j|i)的相对大小，但它不涉及到i,j的交互，可以用来表达一些绝对信号，比如Scissorhands表明某些绝对位置的token的注意力一直都会很高，这就有可能用‖kj‖来表达；
剩下的cos(qi,kj)就是用来表达i,j的交互，它是自由度最大的一项。

很明显，为了提高某个位置j的相对重要性，模型有两个选择：
1、增大模长‖kj‖；2、增大cos(qi,kj)，即缩小qi,kj的夹角大小。
然而，由于“维度灾难”的存在，在高维空间中显著地改变夹角大小相对来说没有那么容易，所以如果能靠增大模长‖kj‖完成的，模型会优先选择通过增大模长‖kj‖来完成，这导致的直接后果是：cos(qi,kj)的训练可能并不充分。

假设：【cos(qi,kj) 的训练不充分是Attention无法长度外推的主要原因。】

cos(qi,kj) 的训练不充分，是指被训练过的qi,kj的夹角只是一个有限的集合，而进行长度外推时，它要面对一个更大的集合，从而无法进行正确的预测。
仔细思考YaRN一文的推导就会发现，NTK、YaRN之所以有效，是因为修改了推理阶段RoPE的实现，使得qi,kj的夹角落到原本训练阶段的有限集合中，避免面对没见过的更大的集合，转外推为内插；
ReRoPE则更加干脆，直接截断Window以外的相对位置，这使得推理阶段的位置编码都不会“面生”。
这些技巧一定程度上都间接地验证了这个断言。

从这个断言出发，KeyNorm的长度外推起因就变得简单了。
不论是只进行KeyNorm的KNA，还是QueryNorm、KeyNorm都做的CosA，它们都将‖kj‖从Attention的定义中排除掉了，于是为了改变j的相对重要性，模型就只有“调整cos(qi,kj)”这一个选择，这将会使得模型更加充分地训练和利用cos(qi,kj)，从而间接促进了长度外推性。
此外，笔者也实验过“KeyNorm + NoPE”的组合，但并没有发现长度外推性，这说明RoPE也在KeyNorm的长度外推中担任重要角色。事实上这也不难理解，RoPE对qi,kj进行旋转，更有助于扩大训练期间cos(qi,kj)的范围，从而使得cos(qi,kj)的训练更为充分。

有没有工作已经尝试过QueryNorm和KeyNorm了呢？有。
2020年的论文《Query-Key Normalization for Transformers》曾实验过CosA，论文还提出了一个类似的长度对数的Scale因子，但没有讨论到长度外推问题。
此外，今年初Google的论文《Scaling Vision Transformers to 22 Billion Parameters》也在Query和Key加了Norm，但加的是LayerNorm，LayerNorm或者RMSNorm都带有可学的gamma参数，这使得Norm之后的向量模长未必为常数，因此并不好说是否能达到本文一样的长度外推效果。

3 一些论文方法

3.0 总结

bias类

• Alibi 位置编码

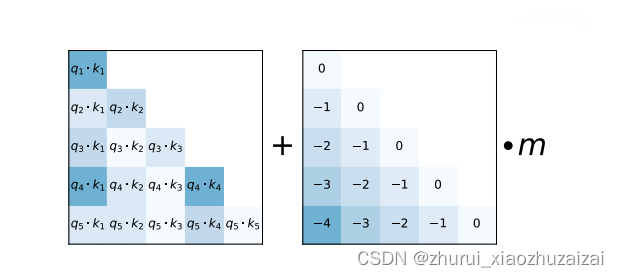
主要是Bloom模型采用，Alibi 的方法也算较为粗暴，是直接作用在attention score中，给 attention score 加上一个预设好的偏置矩阵，相当于 q 和 k 相对位置差 1 就加上一个 -1 的偏置。其实相当于假设两个 token 距离越远那么相互贡献也就越低。
ALiBi的做法其实和T5 bias类似，直接给q*k attention score加上了一个线性的bias：

• KERPLE(Kernelized Relative Positional Embedding for Length Extrapolation)

KERPLE主要针对Alibi 做了一些微小改进，将内积的bias由之前自然数值幂函数或指数函数，并且改成可学习参数。

• Sandwich(Receptive Field Alignment Enables Transformer Length Extrapolation)

Sandwich将ALiBi的线性bias改为正弦编码的内积pm*pn，上述编码也是对于正余弦三角式的一种改进。

插值类

• Extending Context Window of Large Language Models via Positional Interpolation

网友@kaiokendev在他的项目SuperHOT中实验了“位置线性内插”的方案，显示通过非常少的长文本微调，就可以让已有的LLM处理Long Context。几乎同时，Meta也提出了同样的思路，带着丰富的实验结果发表在论文《》上。
通过位置插值来扩展大语言模型的上下文窗口
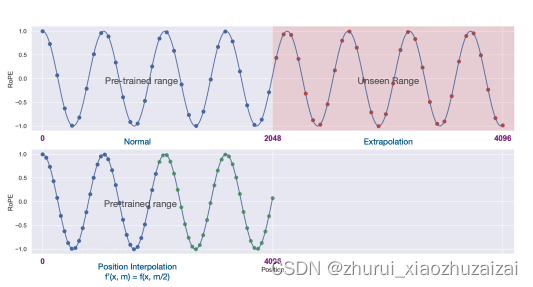
关键思想是，我们不进行外推，而是直接降低位置索引，使最大位置索引与预训练阶段的先前上下文窗口限制相匹配。见图 1 进行说明。
换句话说，为了容纳更多的输入标记，我们在相邻整数位置上插值位置编码，利用位置编码可以应用于非整数位置的事实，而不是在训练位置之外进行外推，这可能导致灾难性的值。我们在理论上验证了我们的方法，通过展示插值的注意力得分具有更小的上界。

NTK-Aware Interpolation
NTK-by-parts Interpolation
Dynamic NTK Interpolation
YaRN

• ReROPE

• HFWA

3.1 有关bias的：Alibi->KERPLE->Sandwich

3.1.1 Alibi

论文：Attention with Linear Biases (ALiBi).

ALiBi的做法其实和T5 bias类似，直接给q*k attention score加上了一个线性的bias：

3.1.2 KERPLE

论文： KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation

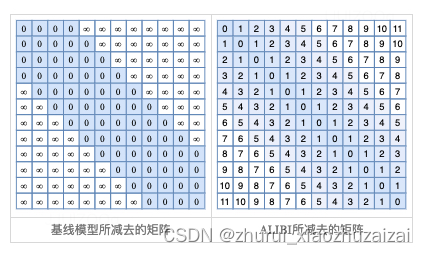
其对ALIBI进行了一些改进，引入了两个可学习的参数r1和r2来“动态”学习局部区域。如下图所示，左侧为原始的通过引入参数Q_m^TK_n来动态减去AIBLI中的λ∣m−n∣矩阵：

KERPLE其实就是ALiBi的一个简单推广，将线性bias改为幂函数或指数函数的形式，系数或幂设置为可学习参数：

定义了两种模式，分别是power和logarithmic，分别对应没有对数和有对数的形式：

在logarithmic模式中，r1控制了整体的量，r2相当于ALIBI中的λ \lambdaλ，c是一个常数。苏神版简化写作:

3.1.3 Sandwich

论文：Receptive Field Alignment Enables Transformer Length Extrapolation

Sandwich与KEPRLE是同一个作者提出的，其对KEPRLE进行了少量改进，即对应的公式改写为：Q_m^TK_n + λ P_m^TP_n，其中P_m和P_n可以使用Sinusoidal编码表示，即：

由于Sinusoidal编码在单调性上等价于∣ m − n ∣，都是线性递增形式，因此Sandwich只是改头换面了。

P_m^TP_n是m−n的标量函数，并且平均而言是|m−n|的单调递增函数，所以它的作用也跟−λ|m−n|相似。之所以强调“平均而言”，是因为P_m^TP_n整体并非严格的单调，而是振荡下降，如图所示：

3.2 插值方法

3.2.1 Positional Interpolation]

论文： Extending Context Window of Large Language Models via Positional Interpolation

我们能否扩展现有预训练 LLM 的上下文窗口？
一种直接的方法是对现有预训练 Transformer 进行微调，使其具有更长的上下文窗口。然而，根据经验，我们发现通过这种方式训练的模型对于较长的上下文窗口适应速度很慢。在训练了 10000 个批次以上后，有效上下文窗口的增加非常小，这表明这种方法不适用于显著延长上下文窗口。

尽管一些技术（如 ALiBi 和 LeX）可以实现 Transformer 的长度外推，即在短上下文窗口上进行训练，然后在更长的上下文窗口上进行推理，但许多现有的预训练 LLM，包括 LLaMA（Touvron 等人，2023），使用具有较弱外推性质的位置编码（例如 RoPE）。因此，这些技术在扩展这些 LLM 的上下文窗口大小方面的适用性仍然有限。

在这项工作中，我们引入了位置插值技术，以实现对某些现有预训练 LLM（包括 LLaMA）的上下文窗口扩展。关键思想是，我们不进行外推，而是直接降低位置索引，使最大位置索引与预训练阶段的先前上下文窗口限制相匹配
换句话说，为了容纳更多的输入标记，我们在相邻整数位置上插值位置编码，利用位置编码可以应用于非整数位置的事实，而不是在训练位置之外进行外推，这可能导致灾难性的值。我们在理论上验证了我们的方法，通过展示插值的注意力得分具有更小的上界。

3.2.2 插值 NTK-Aware Interpolation

NTK-Aware Interpolation以NTK（神经正切核）作为理论支撑，或者说灵感来源。作者认为高频信息对于神经网络非常重要，而Position Interpolation对于向量的所有分组不加区分地缩小旋转弧度，降低旋转速度（进一步体现为对其正弦函数进行拉伸），会导致模型的高频信息缺失，从而影响模型的性能。

在前文中我们介绍过，位置越靠前的向量分组，旋转速度越快，频率越高，作者希望保留这些高频信息。在NTK-Aware插值中，经过调整后，位置m的旋转弧度如下公式所示，其中LLaMA中的base为10000， α表示base的缩放因子：

我们以Code LLaMA为例进行分析，Code LLaMA中 α=100，也就是将原始模型的 base 放大100倍。调整后的旋转弧度与原始旋转弧度的倍数关系如下：

原始ROPE：

其中θ_i = 10000^-2i/d, ROPE可以表示为[cos mθ_i, sin mθ_i],
做个变换：θ_i = 10000^2i/d，那么 ROPE可以表示为[cos m/θ_i, sin m/θ_i],

十进制数n转化为β进制，其第i位的数字应该是n/β^i-1 mod β，
其可以表示为[n/β⁰, n/β¹, n/β²,n/β³,n/β⁴ ……]

ROPE比较：[cos m/β⁰, sin m/β⁰, cos m/β¹, sin m/β¹, cos m/β², sin m/β²……], β= 10000^2/d

需要扩大k倍，将10000换成10000k

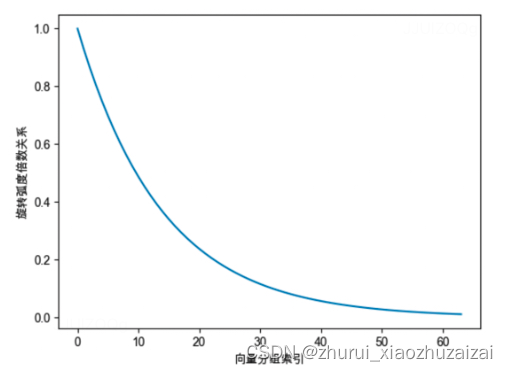
如下图所示，越靠后的分组，旋转弧度缩小的倍数越大。其中第0分组的旋转弧度保持不变，最后一个分组的旋转弧度变为原来的1/100。可以将NTK-Aware Interpolation的思想总结为：保留高频信息；高频分量旋转速度降幅低，低频分量旋转速度降幅高；在高频部分进行外推，低频部分进行内插。

评测结果表明，在不进行finetune的时候，NTK-Aware插值的效果比线性插值更优。

为什么NTK-Aware Interpolation能够奏效？作者以NTK的理论进行解释。但我们认为从旋转周期的角度也许可以进行更加直观且合理的解释。前文中我们介绍过，位置越靠后的分组的旋转速度越慢，频率越低，周期越长。如下图所示，对于第0组分量，仅在位置7时，就已经旋转一周。但对于第64组分量，当位置为2047时，其旋转弧度约为0.2047，甚至仍未完成1/4周旋转。

我们可以将NTK-Aware Interpolation奏效的原因按照如下方式进行解释：

靠前的分组，在训练中见过非常多完整的旋转周期，位置信息得到了充分的训练，所以具有较强的外推能力。
靠后的分组，在训练中无法见到完整的旋转周期，或者见到的旋转周期非常少，训练不够充分，外推性能弱，需要进行位置插值。

NTK-RoPE成功地成为目前第二种笔者测试有效的不用微调就可以扩展LLM的Context长度的方案（第一种自然是NBCE）

3.2.3 NTK-by-parts Interpolation

NTK-by-parts Interpolation则是基于NTK-Aware Interpolation进行优化，其核心思想是：不改变高频部分，仅缩小低频部分的旋转弧度。也就是不改变靠前分组的旋转弧度，仅减小靠后分组的旋转弧度，这就是by-patrs的含义。

3.2.4 Dynamic NTK Interpolation

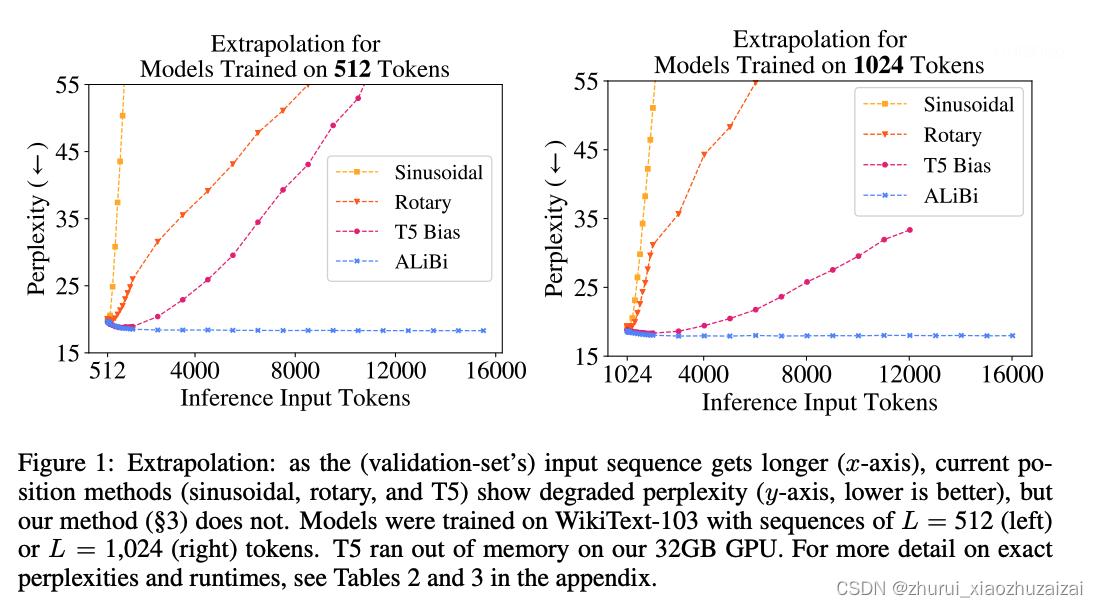
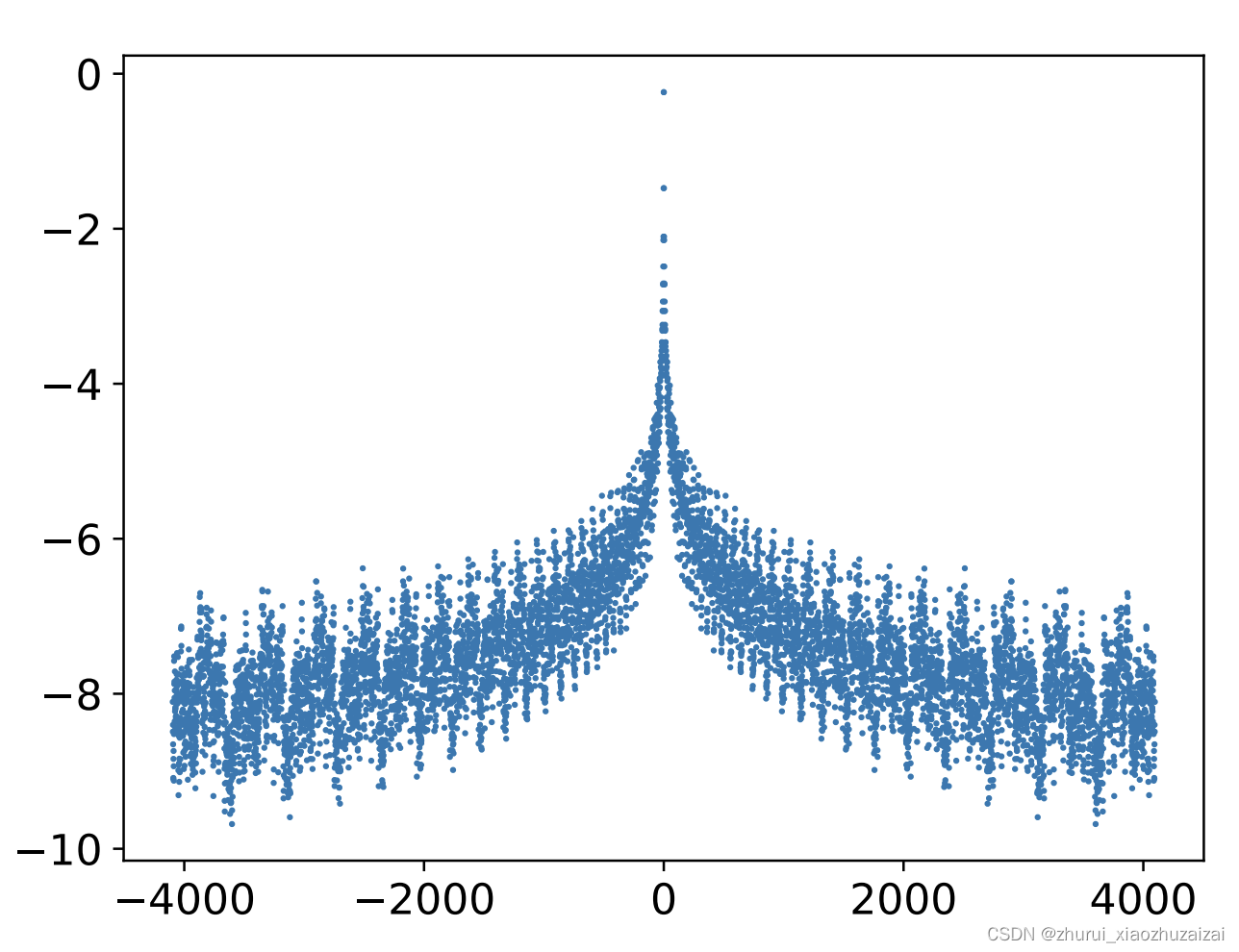
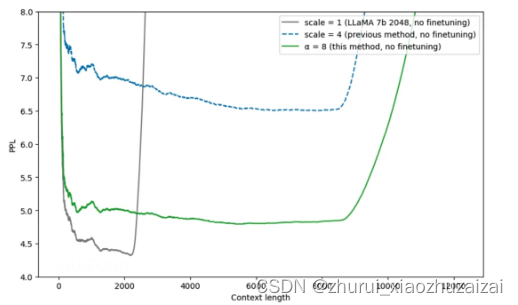
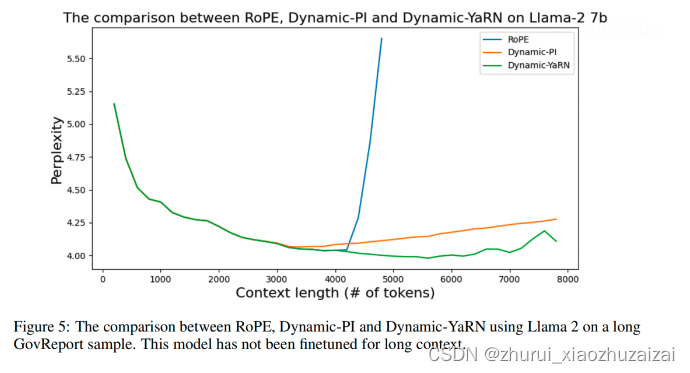
当超出训练长度时，上述插值方法都比原模型直接外推的效果更好，但是它们都有一个共同的缺点，在训练长度内，推理表现都比原模型差。如下图，灰色表示LLaMA直接外推的表现，在2048长度内，原始模型的困惑度显著低于各种插值方法。[如上面的PPL图]
Dynamic NTK Interpolation是一种动态插值的方法，思路也很简单：推理长度小于等于训练长度时，不进行插值；推理长度大于训练长度时，每一步都通过NTK-Aware Interpolation动态放大base。

3.2.5 YaRN

前文中我们介绍过，无论是Position Interpolation还是NTK类方法，本质都是通过减小旋转弧度，降低旋转速度，来达到长度扩展的目的。这将导致位置之间的旋转弧度差距变小，词向量之间的距离变得比原来更近，词向量之间的点乘变大，破坏模型原始的注意力分布。所以经过插值之后，模型在原来的训练长度内的困惑度均有所提升，性能受损。

向量的内积公式如下。向量旋转不改变模长，当 q和 k 的旋转弧度变小，导致它们之间的夹角 变小，所以两者的内积会变大，最终会改变模型的注意力分布。

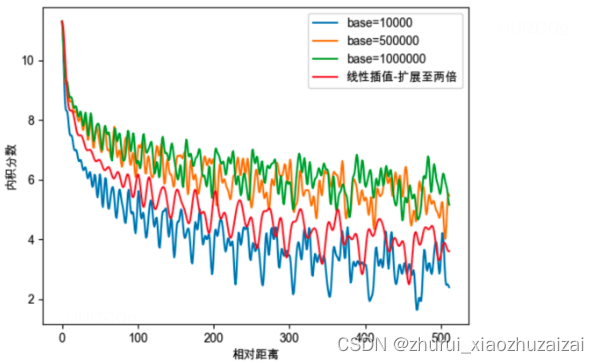
我们以图像的方式进一步分析注意力分布变化的问题。初始化两个全一向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。对于不同的长度扩展策略，q和k的内积变化如下图。无论是NTK还是线性插值，相对距离固定时，q和k之间的内积分数都将变大，进而导致模型的注意力分布改变。并且可以发现，RoPE的注意力远程衰减的性质变弱，这也将导致整个序列的注意力分布变得更加平滑。

YaRN本质上是NTK-by-parts Interpolation与注意力分布修正策略的结合，仅缩小低频部分的旋转弧度，且通过温度系数修正注意力分布。只需将原来的注意力分数除以温度 t 即可。

我们以LLaMA为例，当长度从2048扩展至16384时，长度扩展为原来的8倍，代入公式，计算得到 t=0.6853 。回顾温度系数对注意力分布的影响，当 t 变大，注意力分布更加平滑，方差更小；当 t 变小，注意力分布更加尖锐，区分度变大，方差变大。t=0.6853 意味着缓解注意力分布过于平滑的问题，让注意力分布方差更大些。
下图是未经过微调的动态插值方法的比较，修正了注意力分布的Dynamic-YaRN，显著优于未修正注意力分布的Dynamic-PI方法。

一句话总结各种方法的特点：
Position Interpolation：目标长度是原来的n倍，则旋转弧度减小至原来的1/n。
NTK-Aware Interpolation：增大RoPE的base，保留高频信息；高频分量旋转速度降幅低，低频分量旋转速度降幅高；在高频部分进行外推，低频部分进行内插。
NTK-by-parts Interpolation：不改变高频部分，仅缩小低频部分的旋转弧度。
Dynamic NTK Interpolation：推理长度小于等于训练长度时，不进行插值；推理长度大于训练长度时，每一步都通过NTK-Aware插值动态放大base。
YaRN：NTK-by-parts Interpolation与注意力分布修正策略的结合，通过温度系数修正注意力分布。

3.3 ReRope

3.3.1 Leaky ReRoPE

只要w小于训练长度，那么通过控制k，我们就可以在精确保持了局域性的前提下，使得所有位置编码不超过训练长度，简单直接地结合了直接外推和位置内插。

3.3.2 ReRoPE（Rectified RoPE）

特别地，矩阵(3)还有一个特别的case：当k→∞时，它简化为

其中w是窗口宽度，大概取训练长度的1/4到1/2，k用来调节可处理的最大长度，
一般使得w+(L−1−w)/k不超过训练长度的一半为佳。
至于ReRoPE，则是直接取了k→∞的极限：

3.3.3 InvLeaky ReRoPE（Inverse Leaky ReRoPE）

作为一种免训练的外推方案，ReRoPE和Leaky ReRoPE的效果都是相当让人满意的，既没有损失训练长度内的效果，又实现了“Longer Context, Lower Loss”。
唯一美中不足的是，它们的推理速度相比原本的Attention来说是变慢的，并且目前尚不兼容Flash Attention等加速技术。

那么，能否让训练阶段变慢，让推理阶段变为常规的RoPE？
ReRoPE/Leaky ReRoPE是一种长度外推方法，场景是“Train Short, Test Long”，训练速度的变慢是短期的、可控的，推理速度的变慢才是长期的、难顶的，所以相较之下，如果是同等程度的变慢的话，我们更愿意将变慢的部分放到训练阶段。

在训练阶段使用Leaky ReRoPE，并让它窗口外的步长大于1，那么按照“推理阶段窗口外使用更小的步长”的原则，推理阶段窗口外是否就可以使用等于1的步长，从而退化为RoPE了？
在训练阶段使用k=1/16,w=128的Leaky ReRoPE，在推理阶段使用正常的RoPE

3.4 HFWA

3.4.1 HFWA

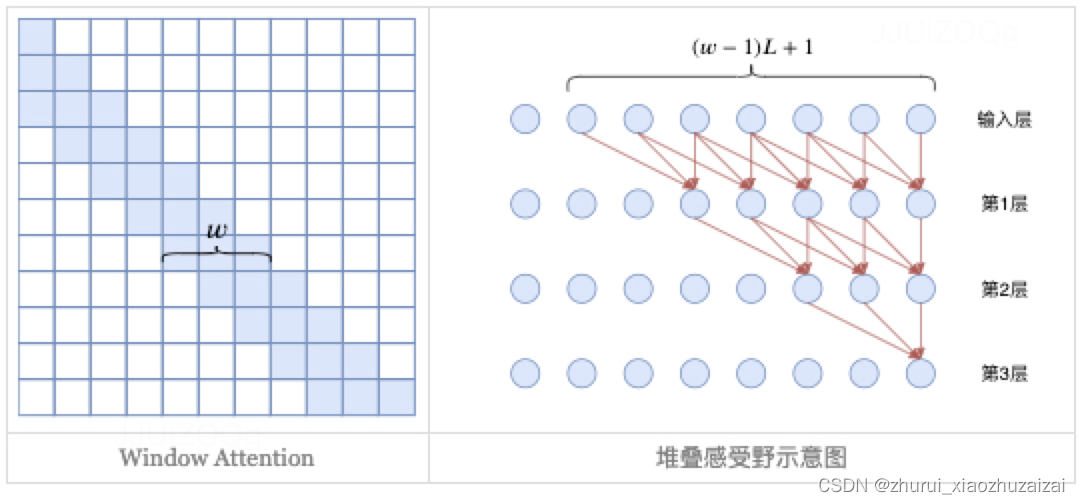
具体来说，HWFA是“L−1层Window RoPE Attention + 1层Full NoPE Attention”，
即前面L−1层Attention都加上RoPE，并通过window限制感受野，这样一来推理成本就变为常数，并且基于block parallel进行优化的话，也可以提升训练速度；
至于最后一层Attention，则保留global的形式，但去掉位置编码（NoPE），同时加上logn缩放。
经过这样修改，并且适当选择window之后，模型的训练效果只有轻微下降，同时呈现出优秀的长度外推能力。

3.4.2 FOT

无独有偶，后来Google提出了FOT（Focused Transformer），它跟HWFA有很多异曲同工之处：
同样是L−1层Local Attention加1层Full Attention，Full Attention同样是NoPE的，
不同的是FOT把Full Attention放在中间，并且Local Attention没有严格限制感受野，所以无法直接长度外推，因此它提出了crossbatch training来拓展模型长度。
事后，笔者实验过在HWFA上使用crossbatch training，也有不错的效果。

3.4.3 HWFA介个ROPE

由于RoPE的特殊性，原始的ReRoPE实现需要算两次Attention矩阵，并且不兼容主流的Flash Attention加速等。总的来说，推理阶段的成本增加略有点大。
不过，HWFA的加入将会极大地缓解这个问题！

训练阶段将HWFA原本的Full NoPE Attention换成Full RoPE Attention，
然后推理阶段则改为Full ReRoPE Attention。
这样一来推理阶段切换ReRoPE带来的额外成本就会变得非常少，而且其他层换为Window Attention带来的收益更加显著。

除此之外，“HWFA+ReRoPE”还可以弥补原本HWFA的效果损失。

此前，为了保证长度外推能力，HWFA的Full Attention要去掉位置编码（即NoPE），同时Window Attention的感受野w̃ 要满足(w̃ −1)(L−1)+1=αN（其中L是层数，N是训练长度，0<α≤1），这些约束限制了模型的表达能力，导致了训练效果变差。
而引入ReRoPE之后，Window Attention的感受野可以适当取大一些，Full Attention也可以RoPE，还可以将它放到中间层而不单是最后一层，甚至也可以多于1层Full Attention。这些变化都可以弥补效果损失，并且得益于ReRoPE，长度外推能力并不会有所下降。