MATLAB环境下基于短时傅里叶变换和Rényi熵的脑电信号和语音信号分析_时频 renyi熵 matlab

傅里叶变换是不能很好的反映信号在时域的某一个局部范围的频谱特点的，这一点很可惜。因为在许多实际工程中，人们对信号在局部区域的特征是比较关心的，这些特征包含着十分有用的信息。这类信号因为在时域(或者是空间域)上具有突变的非稳定性和特点，他们的频谱均匀地分布在整个信号的频率轴上，用傅里叶变换的形式进行分析往往并没有那么高效。为此对这类信号必须考虑采用其他的方法，通常的解决办法就是引入一个局部的频率"参数"，这样一个局部傅里叶变换就可以直接通过一个窗口来分析该类信号，在这个窗口内的信号近似也就是稳定的。另外一种等效方法则是修改傅里叶变换的正交基函数。短时傅里叶变换和小波变换就是根据上述原理建立并提出来的。

熵最早用来在热力学中表示物质状态的概率，之后又被引入到数学和信息论中，分别表示问题的不确定性以及系统的复杂性。Shannon熵是为了解决新的度量问题而被提出的。随着理论的不断深入与拓展，Shannon理论已被应用到数学、现代动力系统等自然科学和社会科学中，用来描述“不确定性”。随机事件或随机变量可以用来描述事件的不确定性，随机变量不同，Shannon熵的定义也不同。

Rényi熵是对Shannon熵的推广，可以用来判断信号的信息量和复杂度，被广泛应用于图像配准、无线电频谱感知以及生物医学领域等领域的信号处理。Rényi熵是一个无量纲指标，当概率集的所有值几乎相等时，Rényi熵的值较大，对应的系统复杂度较大；如果只有少数值是大的，而其他值保持较小，Rényi熵的值较小，对应的系统复杂度较低。

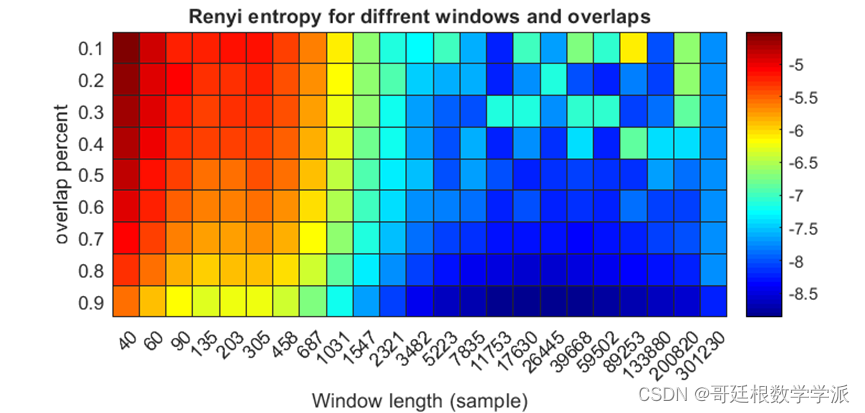
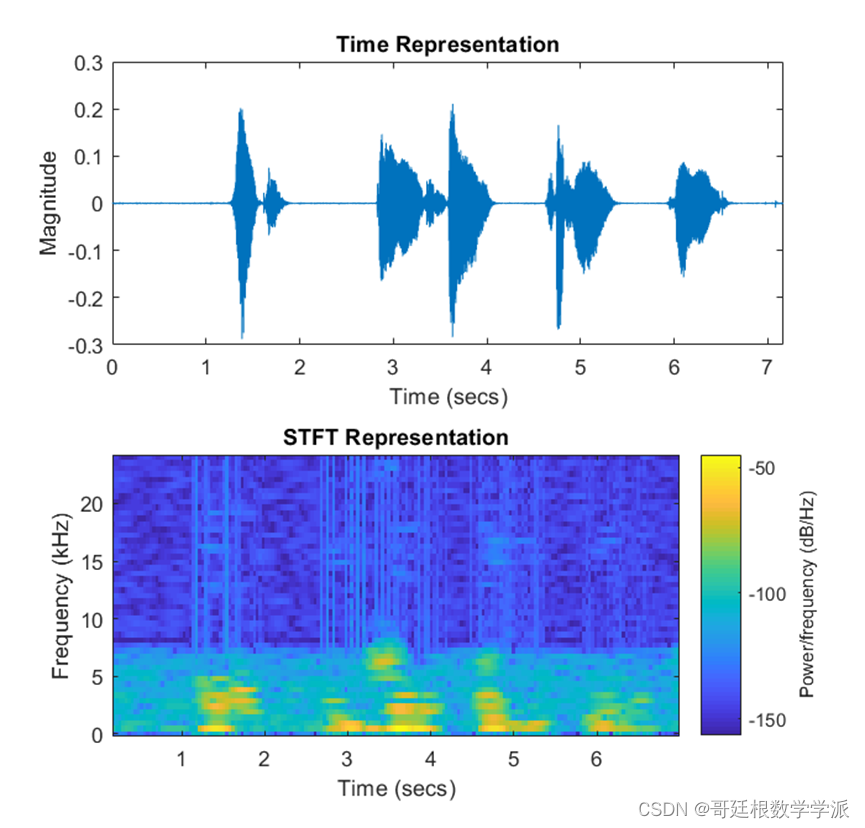
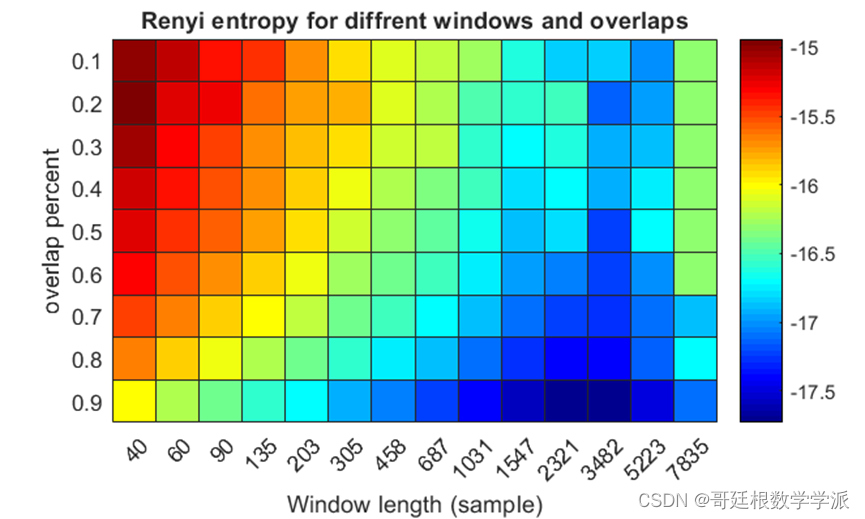
该代码为MATLAB环境下基于短时傅里叶变换(STFT)和Rényi熵的脑电信号和语音信号分析，部分代码如下：

%% Plot Renyi Amount in heatmap
figure();
renyi_heat_map = heatmap((renyi));
renyi_heat_map.Colormap = colormap(jet);
renyi_heat_map.XData = windowval;
renyi_heat_map.YData = overlap_percentage;
xlabel("Window length (sample)");
ylabel("overlap percent");
title("Renyi entropy for diffrent windows and overlaps")

程序出图如下：

工学博士，担任《Mechanical System and Signal Processing》审稿专家，担任《中国电机工程学报》优秀审稿专家，《控制与决策》，《系统工程与电子技术》，《电力系统保护与控制》，《宇航学报》等EI期刊审稿专家，担任《计算机科学》，《电子器件》 ， 《现代制造过程》 ，《电源学报》，《船舶工程》 ，《轴承》 ，《工矿自动化》 ，《重庆理工大学学报》 ，《噪声与振动控制》 ，《机械传动》 ，《机械强度》 ，《机械科学与技术》 ，《机床与液压》，《声学技术》，《应用声学》，《石油机械》，《西安工业大学学报》等中文核心审稿专家。
擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。