KMP算法及其优化——串模式匹配算法_kmp优化算法字符串每趟匹配过程

KMP（Knuth Morris Pratt）算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

模式匹配的改进算法——KMP算法是在O(m+n)的数量级上完成串的模式匹配。算法的改进之处在于：每当1趟匹配过程中出现字符比较不等时，指向主串的指针i不会溯，而是利用已经得到的“部分匹配”的结果将模式串向右滑动尽可能远的一段距离后继续进行比较。

例：
主 串 : S=a c a c b a c b a a b c a
模式串:T=a c b a b

如图所示，在匹配过程中，第1次比较不成功时，i=3，j=3，此时i指针不变，仅需将模式串T向右移动2个字符的位置，继续进行i=3，j=1的下一趟比较；第2趟匹配中，前4个字符比较成功，但i=7，j=5时比较失败，此时将模式串向右移动3个字符的位置，继续进行i=7，j=2的下一趟比较，直至比较成功。在整个匹配过程中，i指针不回溯。

可是我们怎么知道每趟匹配移动的位置呢？

为此，我们定义一个数组从而记录每趟模式串移动的位置next[ j ]函数，表明当模式中第j个字符与主串中相应字符“失配”时，在模式串中需重新和主串中该字符进行比较的字符的位置。

next函数

• next[ j ]函数定义如图：
  

下面就next函数进行介绍：

• max意为最大值，即模式串匹配失败字符前的所有字符，所有能满足头部与尾部向同的最大长度。（此处最难理解）
  下面进行解释：
  
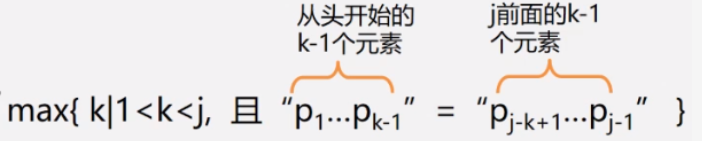
  上图中，max=k，而条件是（k-1）个元素，意为若存在前三个与后三个相同则k-1=3；k=4；此时next值=max=k=4；

  例1：如图一（本文章第一张图片）所示在第三趟匹配中是从j=2开始匹配，即next值是2，那么反过来max=2；k-1=1；意思是模式串中匹配失