Codeforces Round #698 (Div. 2) 补题_codeforces698

A题

直接猜的。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=110;
int a[N];
void solve()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    int res=1;
    int ans=0;
    for(int i=2;i<=n;i++)
    {
        if(a[i]==a[i-1])
        {
            res++;
        }
        else 
        {
            ans=max(ans,res);
            res=1;
        }
    }
    ans=max(ans,res);
    cout<<ans<<endl;
}


int main()
{
    int t;
    t=1;
    cin>>t;

    while(t--)
    {
        solve();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

B题

• 思路
  如果a[i]>10*d的话，直接yes，因为例如7，70-79都对，80以后的数字都可以用71-79加上一个7的倍数表示。
  小于直接打表。
• 代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

const int N = 1e4 + 10;

ll a[N];

bool get_s(ll x, ll d)
{
    bool flag = true;
    string s = to_string(x);
    for (int i = 0; i < s.length(); i++)
    {
        if (s[i] - '0' == d)
        {
            flag = false;
            break;
        }
    }
    if (!flag)
        return true;
    else
        return false;
}

void solve()
{
    ll q, d;
    cin >> q >> d;
    for (int i = 1; i <= q; i++)
        cin >> a[i];
    ll dp[11] = {-1};
    for (int i = 1; i <= 9; i++)
        dp[i] = (d * i) % 10;
    for (int i = 1; i <= q; i++)
    {
        if (get_s(a[i], d))
        {
            cout << "Yes" << endl;
        }
        else
        {
            ll x = a[i] % 10;
            bool flag = false;
            if (a[i] % d == 0)
            {
                cout << "Yes" << endl;
                continue;
            }
            if (a[i] >= d * 10)
            {
                flag = true;
                cout << "Yes" << endl;
                continue;
            }
            for (int j = 1; j <= 9; j++)
            {
                if (x == dp[j])
                {
                    if (a[i] >= j * d)
                    {
                        flag = true;
                        cout << "Yes" << endl;
                        break;
                    }
                    else
                        continue;
                }
            }
            if (!flag)
            {
                cout << "No" << endl;
            }
        }
    }
}

int main()
{
    int t;
    t = 1;
    cin >> t;

    while (t--)
    {
        solve();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

C题

注：

某个大佬的，侵权删除。

D题

• 题意
  

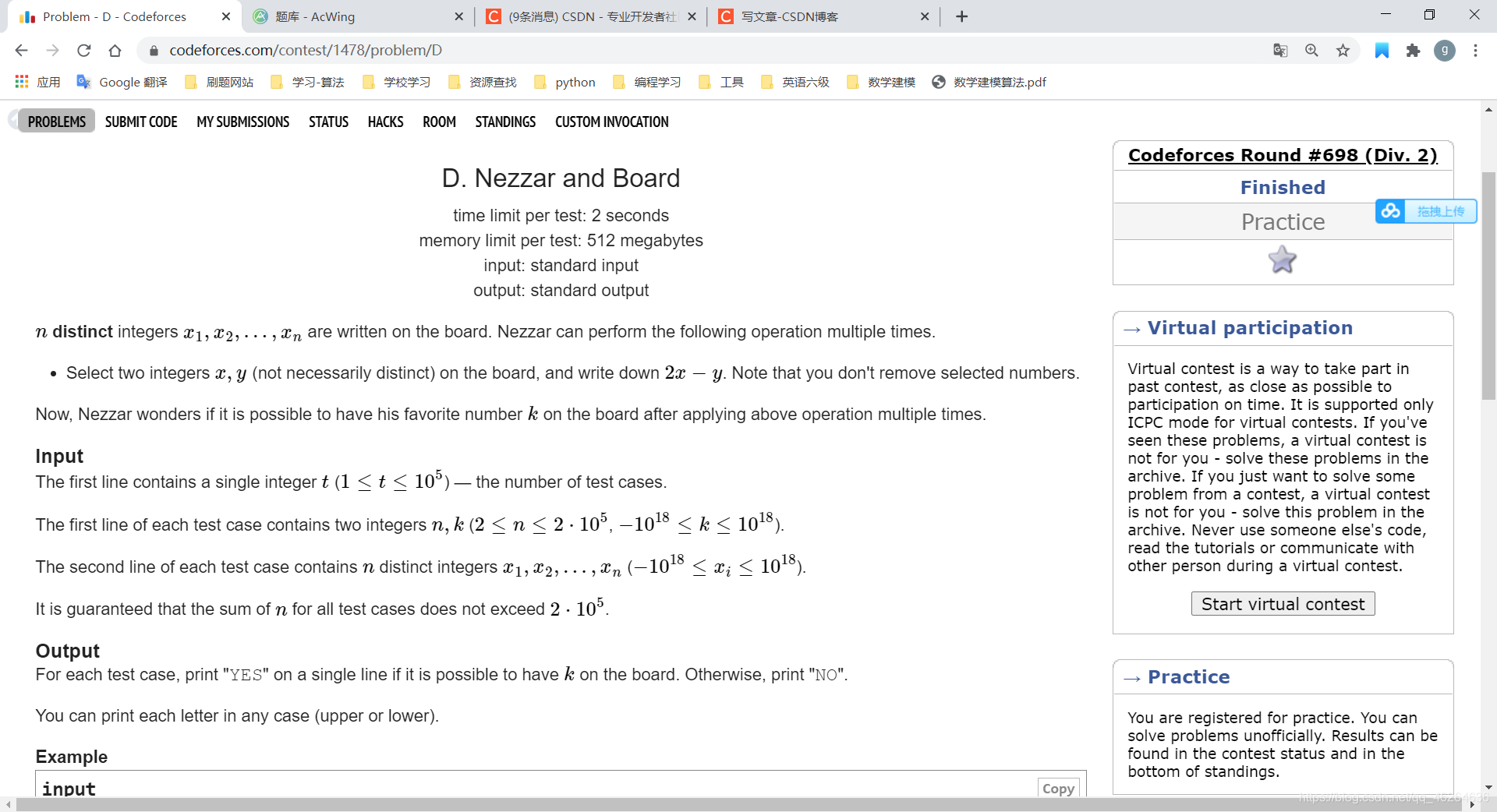
• 思路
  因为2*x-y=x+x-y,相当于加上和任意数的差，所以只需要判断一下数组中的任意一个是否能够加上多少称为k。加上多少的这个数就是所有数差的gcd。

• 代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long 
ll a[202020];

int main()
{
    ll k,n,t,T=1;
    cin>>T;
    while(T--)
    {
        cin>>n>>k;
        for(int i=1;i<=n;i++)
            cin>>a[i];
        ll g=abs(a[1]-a[2]);
        for(int i=3;i<=n;i++)
            g=__gcd(g,abs(a[i]-a[i-1]));
        if((k-a[1])%g==0)
            cout<<"YES"<<endl;
        else
        cout<<"NO"<<endl;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25