- 1AI一键图文生成短视频工具,文章AI自动生成视频,傻瓜式操作。_免费ai多个图片自动生成小视频
- 2codeforce gym 101726 problem D Poker
- 3【云端风云:云计算全局解密】一篇文章读懂云计算技术及其未来发展趋势(一万八千字)_云计算解密成果
- 4计算机嵌入式三级_宾格果
- 5大语言模型参数说明(Temperature,Top p,Top k)_模型temperature
- 6手把手教你写HT1621显示驱动,简单明了,内含原码,方便移植,_tm1621d驱动问题
- 7麦克风基本知识_话筒600和800频率区别
- 8pandas读取txt_pandas read txt
- 9火车头采集伪原创插件_火车头伪原创插件
- 102024年最火AI视频祝福告白创作系统SaaS版源码正式上线了抖音小程序微信小程序公众号源码搭建坑位多种模式合作_2024年最火ai视频祝福告白创作系统saas版源码正式上线了,新年倒计时,注册登录免费
信号调制的工作原理_信号调制的思路是用信息乘以低频波仔
赞
踩
要理解如何进行无线数据传输,我们需要了解:
-
什么是频率?
-
信息/数据信号 时间表示
频率表示,为什么它很重要?
-
滤波器如何工作?
-
FCC通信频段
-
调制和解调
这些主题可能您在大学专业课上学过,其中涉及非常庞大的知识。此前我为高级项目组中非电子工程专业的学生准备的PPT中,配套介绍了这些主题――学生们期望能够弄清楚我们谈到的“900MHz”、“2.4GHz”或“跳频”等术语。本文限于篇幅,难以对这些主题的阐述完整、彻底,忽略了专业课所涉及的很多细节,仅提供无线传输方面的概念性说明。
什么是频率?
频率是描述每隔多长时间振荡一次或重复一次的术语,单位为赫兹(Hz)或秒的倒数。如果每秒振荡60次,则其频率为60Hz。在本文中,我们将主要探讨音频波(气压的振荡),及其如何以数百千赫频率从无线电台传播到您的车载收音机上(或任何AM无线电台)。任何波都有一个频率,光波也一样。光波和其他更高频率的波(例如X射线、伽马射线、微波)一般用波长来表示,而不用频率。例如,绿色光的波长大约为400纳米。下图显示了行进波单位间的关系:

正弦波的基本单位
假设信号速度恒定,则波长和频率是可以换算的,不过这已超出本文的讨论范畴。 不同复杂性的信息信号 如果发送一个纯正弦波信号(称为“音频”)。它不携载任何实际信息,听上去也并不好听。下图是一个正弦波的图像,X轴为时间,Y轴为电压,这是一个150Hz参考信号。

单音频信号(时域)
那么为什么要看这幅图像呢?让我们来看一下时域中复杂性不断增加的信号。这是一个双音频信号(两个音频叠加在一起)。此正弦波与上一个正弦波相同,只不过又加上了另一个倍频(300Hz)的正弦波。

双音频信号(时域)
那么由多个不同频率的音频组成的信号是什么样的呢?

多音频信号(时域)
它变得毛刺更多。您能在此图中看到的唯一真实信息便是在指定时间内的电压电平。这就是信息的本质,它极其重要——但也使分析变得复杂,更使了解调制工作变得更加困难。为此,您可能希望用另一种不同的方式(频域)绘制信号图像。它显示信号在一系列频率上的强度。让我们看一下。 为何信号的频谱很重要? 要将大量信号转换到频域中,需要进行精密的数学运算。这项工作很困难,计算量很大,必须反复练习才能掌握。我甚至定期对那些重要信号的进行卷积运算,练习我的转换能力。不管怎样,让我们看一下以上三个信号如何用这种形式来表示(这里忽略中间的推演运算)。我们不再绘制信号电压随时间的变化,而是绘制信号功率随频率的变化。

单音频信号(频域)

双音频信号(频域)

多音频信号(频域)
注意到图中明显的尖峰了吗?那是正弦波在特定频率(X轴)上的数学表示。理想情况下,这些尖峰应当是无限窄(宽度)和无限高的,但是受我所使用的Spice软件的技术水平限制,它是不完美的。这种信号称为脉冲信号。有关此信号的详细说明,请阅读此处!对于这个音频,我们看到在频域看到一个尖峰,在150Hz处。而双音频信号在频域有两个尖峰,在150Hz和300Hz处。多音频信号在时域中基本无法解读,时域信号中众多的小尖峰,是多个频率点的叠加组成的。
最后举一个例子,一个实际的音频信号。如下图,我采样了15秒歌手Cream的歌曲《白色的房间(WhiteRoom)》。不必为信号长的摸样担心,在EricClapton的吉他独奏期间,任何麦克风都没有损坏。

音频信号 这就是大多数信号的看上去的样子,尤其是模拟信号。人和乐器的声音并不是在离散的频率上播放,其频率内容分布在整个频率范围内(尽管某些内容几乎是听不到的)。这个范围在3Hz至20kHz之间,大约就是人耳能够听到的频率范围。低音部的频率较低,高音部的频率较高。Y轴标度用dB表示,dB表示一个比例,没有单位。在本质上来说,dB值越高,那个频率对应的信号就越高。 理论上,我们可以用无数个音频信号累加之和来表示这个模拟信号。 滤波器! 幸好频域的图形表示可为滤波器设计提供一些帮助。滤波器有四种类型,包括:
-
低通滤波器:高于“截止频率”的所有频率都被滤除。
-
高通滤波器:低于“截止频率”的所有频率都被滤除。
-
带通滤波器:距离“中心频率”一定范围外的所有频率都被滤除。
-
带阻滤波器:距离“中心频率”一定范围内的所有频率都被滤除。

由上而下:带通滤波器、低通滤波器、高通滤波器
“3dB”点是信号输出降低大约30%的地方。dB是一个对数标度:
x[dB]=10*log(x[linear])
x[linear]=10^(x[dB]/10)
基于这个公式,x[linear]=0.7,对应的x[dB]大约为-3.0dB,0.7就是70%,就是信号衰减30%,这时对应的频率就称为滤波器的截止频率。汽车音响就是一个实际的例子,它可能包括一个“分频器”,其特殊的滤波器设计可将低频切换至低音扬声器、高频切换至高音扬声器。这对于无线接收机是非常重要的。
FCC通信频段
FCC和其他国际组织一致认为,如果任由任何人随意使用任何频率,那么必然会导致绝对的混乱。因此,应为不同用户分配不同的频率范围。例如分别为FM无线电、AM无线电、WiFi、移动电话、海事通信、空中交通管制、业余无线电、对讲机、军事通信、警用电台等应用分配不同频段。对了,我们还没提卫星或空间通信!这真是太乱了,幸亏有FCC帮助管理。如果您感到好奇,不妨用谷歌搜索一下,马上就能找到一个更详细的图表。

FCC频谱分配表
FCC已为小范围的个人应用、业余爱好者的应用和其他常规“ISM频段”应用(工业、科学、医疗)预留了部分频段。这就是WiFi、对讲机、无线传感器和其他通信设备的工作频段。让我们再次讨论一下频率!人耳的听力范围为20Hz至20kHz。如果我们的AM电台为680kHz,那么无线电塔如何将声音变到该频率呢?它如何避免干扰到其他电台?接收机如何将信号频率转换回可听范围?
调制
让我们离开频域,回到时域。再次重申一下:我们的讨论过于简单,略过了很多细节!在此只是为了得到一个概念性的结果。之所以这么说是因为,数学表示最适合在时域中使用,而图形表示在频域中效果最佳。
调制的作用就是将信号从低频(信息)转换到高频(载波)。思路很简单:用您的信息乘以高频载波,例如680kHz,这就是AM广播!稍等一下,事情果真如此简单吗?让我们看几个数学关系式。在此例中,θ就是信息(可听内容),φ是载波(例如,AM广播频率)。


图中文字中英对照
我们的AM信号如果用公式来表达,涉及多个信号的乘法运算,这在时域或频域中是很难想像的,因为我们仅仅看到音频是什么样的。但是上述这种对应关系告诉我们:两个信号相乘可用两个信号相加来表示!现在,我们很容易在频域中绘制出经乘法运算得到的信号。

在载波(1000Hz)上调制的单音频(150Hz)
在此图中,我们用150Hz音频乘以1000Hz载波。上表显示了两个半功率信号,分别位于1000-150和1000+150Hz处,也就是在850Hz和1150Hz处。那么当经过调制后,我们每个音节的表现如何呢?

声音调制到700kHz
不出所料,我们看到了两个信号。一个是载波+信息,另一个是载波-信息(甚至注意到它是如何反转的)。 这就是AM频谱和信号内容的大致图解。

解调 现在我们来讨论接收机。所有信号均从天线开始,在同一时间查看所有信号,看到的是一团乱麻。天线拾取到大量的数据,但它并不负责进行分类,这是调谐器和其他硬件的工作。信号解调的原理与调制原理完全相同,非常方便!要将我们的音频信号转回到“基带”,并将其发送至扬声器,我们可以再次用载波乘以所有信号。
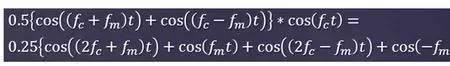
这个公式中包含一大串数学函数、括号和频率变量。不过它是对的,我们由此导出了四个信号:
-
1/4功率信号,(2*载波+信息)
-
1/4功率信号,(信息)
-
1/4功率信号,(2*载波-信息)
-
1/4功率信号,(-信息)
让我们忽略这个包含负频率的项,它是我们讨论调制及涉及的运算时,常常会出现的数学产物。在双倍载波上的两个信号(假设载波远大于信息,它们几乎是相同的)可用低通滤波器滤出。低通滤波器会阻断信号的所有高频内容,于是只将原始信息留给我们。我们可用放大器放大原始信息,然后发送到扬声器。太酷了!这就是它的图像,但是要向后延迟一点。 结论 本文的目的是高度概括地介绍无线电信号是如何传输和调制的。通过将多个音频(或基带)信号乘以不同的高频信号(载波),我们可以通过同一个信道成功传输多个数据流而不会相互干扰。再次用载波相乘,将调制的信号转换回基带,再用低通滤波器和放大器清理并放大信号,即可让我们听到各种美妙动听的声音!
来源:数字测试
—END—
关于RFASK射频问问
射频问问是在"微波射频网”系列原创技术专栏基础上升级打造的技术问答学习平台,主要围绕射频芯片、微波电路、天线、雷达、卫星等相关技术领域,致力于为无线通信、微波射频、天线、雷达等行业的工程师,提供优质、原创的技术问答、专栏文章、射频课程等学习内容。更多请访问:RFASK射频问问 - 射频技术研发服务平台 | 技术问答、专栏文章、射频课程


