devbox
菜鸟追梦旅行
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【C题完整论文】2024美赛完整论文+代码参考（无偿分享）

作者：菜鸟追梦旅行 | 2024-02-25 14:02:34

赞

踩

【C题完整论文】2024美赛完整论文+代码参考（无偿分享）

C题：网球运动中的动力

一、问题分析

1.1 问题一分析

针对该问题，经过数据清洗和特征工程处理之后，即考虑对动量指标的定义，通过数据分析和相关性计算，选取是否发球、是否取得压制性得分、跑动差和失误率这四项指标作为基本的影响指标，通过实验进行权重分配之后，再通过标准化映射将其规约到[-1,1]区间内，从而能够再任意时刻直接计算参赛者的优势大小，最终进行可视化。

1.2 问题二分析

针对该问题，可以通过两个方面来评估，得到“动量”在比赛中的确起作用的观点。通过可视化数据量化表示动量和比赛结果的单调关系，动态展示相关性。并在测试集上计算每步动量和比赛最终胜负的相关关系。通过仿真生成随机的得分方案，进行同样的相关性分析。

1.3 问题三分析

对于第一点，可以通过网络进行特征分析，进行PCA（主成分分析）方法考虑多个指标对最终结果的贡献度，得出最相关的因素。

对于第二点，可以通过识别对方选手的最影响动量的因素，从而针对性进行回避和对抗。例如对方选手如果出现动量上升的预兆，就可以通过暂停等方案进行规避。

1.4 问题四分析

针对该问题，可以将动量模型与最终的胜负联系起来，在所有的数据集上进行误差分析。具体来说，可以将动量结果作为输入，使用另一个模型来进行分类，得出最终的比赛结果。并通过特征工程分析未来可能需要包含的相关因素，最后搜集其他比赛的数据集，进行泛化性验证。

1.5 问题五分析

基于前四个问题归纳总结即可。例如时刻注意动态的动量曲线变化，提早识别出双方对动量曲线影响的因素，从而多使用对自己有利的方案，规避对对方有利的方案等。

二、模型建立与求解

2.1 问题一：

2.1.1 求解思路

针对该问题，经过数据清洗和特征工程处理之后，即考虑对动量指标的定义，通过数据分析和相关性计算，选取是否发球、是否取得压制性得分、跑动差和失误率这四项指标作为基本的影响指标，通过实验进行权重分配之后，再通过标准化映射将其规约到[-1,1]区间内，从而能够再任意时刻直接计算参赛者的优势大小，最终进行可视化。

2.1.2 数据预处理

通常对数据的预处理包括以下几个部分 （1）离群数据处理，将数据集中的异常离群点数据进行处理，通常有滑动平均及直接删除等方法（2）数据记录缺失值处理，往往在采集数据的过程中，数据时间点的统计可能并不连续，从而需要使用窗口均值或是回归等方式进行缺失值的填补；（3）数据标准化，一般是将数据放缩到零均值同方差的区间，确保数据的多个特征的无量纲化。对于附件中收集到的数据，时间较为完整，除少数比赛盘数出现时间大于24之外，不存在过多异常值，所以不进行过度处理。

2.1.3 数据分析

数据一共包括31场比赛场次，来源于2023 Wimbledon Championships 男子单打的32强之后的竞争赛，我们首先认为数据中存在的所有指标都是有意义的，首先进行部分指标的分析。

在统计学中，皮尔逊相关系数，又称作 PPMCC或PCCs，文章中常用r或Pearson' s r表示）用于度量两个变量X和Y之间的相关（线性相关），其值介于-1与1之间. 在自然科学领域中，该系数广泛用于度量两个变量之间的相关程度，主要是用来衡量变量间的线性相关关系。皮尔逊相关系数的计算公式为

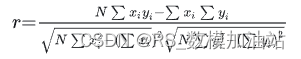
相关系数越接近于1或-1,相关系数的绝对值越大，相关度越强；相关系数越接近于0，相关度越弱。通常情况下通过下表取值范围判断变量的相关强度。

表1 相关强度等级表

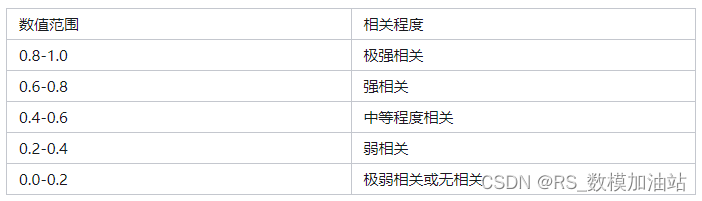
 理论上来说，发球方在当前分下的获胜概率比非发球方更高，我们统计所有发球方与获胜方在数据，进行展示：两者的皮尔逊相关系数r 仅为0.35,体现为弱相关。但绘制其混淆矩阵可以得出：

 

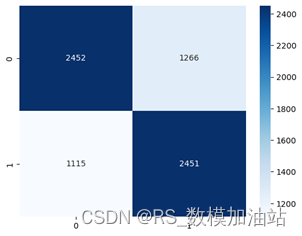
理论上来说，手握发球局，有0.67的概率得分。

其次，压制性得分对动量也有较大影响。压制性得分定义为得到最近A分的B分，这是一个直接描述最近得分势头的指标，相比于连胜得分，它更具有说服力，这是因为在网球中需要频繁交替发球，发球和破发的影响不可忽略。通常考虑B=5，A=4，即如果在最近5小分中拿到4分，对动量提升有较大帮助。下图展示了在决赛的第一盘中（2023-wimbledon-1701，set_no = 1）

 

在该盘中，选手Djokovic的压制性得分以13：0的出现次数压倒性的领先，从而简单的以6：1的局分带走第一盘。

在盘内的选手之间的跑动距离差会很大程度上影响选手的体力，如果在相持阶段被频繁调动，导致跑动距离远大于对方选手，会导致降低整体胜率，从而降低动量。

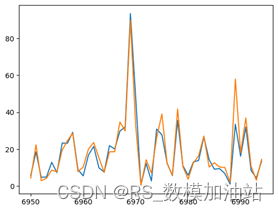
 同样以该盘为例，整体的选手Djokovic总体来说拥有较低的移动量，也最终获得该盘的胜利。

 

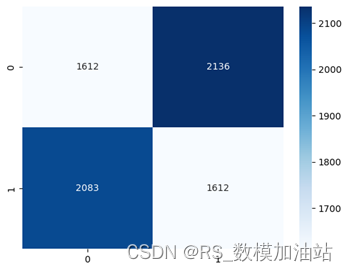
将所有数据整合分析，有57.8% 的概率可以认为跑动距离较长的一方胜率较低，但由于在部分场次中跑动距离相差不大，计算得出平均的跑动距离为13.94，最终的跑动距离指标将与平均跑动距离求差后再进行计算。

此外，数据中提供的两次发球失误并输掉分数（double_fault），非受迫性失误（unf_err）这两个指标失误指标会显著性降低动量，虽然不会对选手生理上造成过大的消耗，但会使选手的心理层面上出现懊悔等情绪，降低胜率。

将指标量化，认为

其中t表示得分发生的时间， St 表示发球指标， Gt 表示压制性得分指标， Rt 表示调动性参数， Ft 表示失误性指标，而 f(⋅) 为标准化函数，进行非线性区间映射，其中 α,β,γ,δ 为不同指标的标准化放缩权重，通过参数寻优，可计算出

我们认为动量应该是一个与净胜场无关的变量，因为我们需要使用动量还刻画逆袭这种状态。

模型构建完毕，我们尝试使用该模型在第一场球赛（2023-wimbledon-1301）中进行可视化分析：

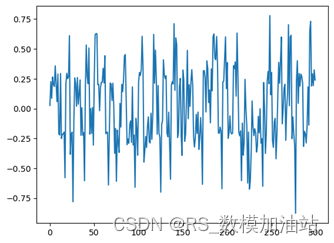
 最终得到决赛的动量展示图5。

 

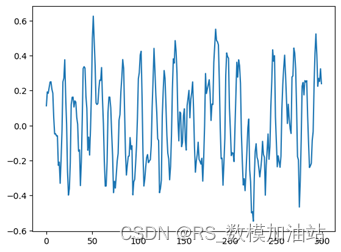
由于其存在一定平稳特性，f(\cdot )为窗口为3的平均滑窗，则最终为图6所示结果，其中其动量求和为6.85大于0，且其中动量大于0等时刻也多于一半。

在实际比赛过程中，由于选手1以6：4先下一城，随后选手2以6：7扳回一局，最后选手1以6：3获得胜利从而获得正常比赛的胜利，图7为整体的净胜场图能够反应这个比赛的趋势，

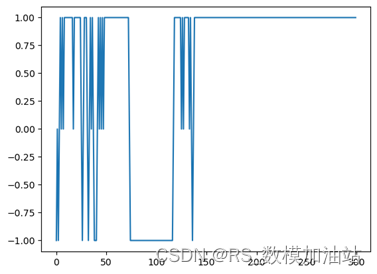
 而不考虑胜场所带来影响的动量，计算其积累量时，也能够反应这种趋势，动量在很大程度上会受到发球局的影响，所以不断震荡，但是还是能够反应选手之间的能力强弱。

  1. import matplotlib.pyplot as plt
  2. import numpy as np
  3. import pandas as pd
  4. from datetime import datetime, timedelta
  5. src_data = pd.read_csv("Wimbledon_featured_matches.csv")
  6. src_data
  7. len(src_data)
  8. src_data.iloc[2,0]
  9. count = 1
  10. for i in range(1,len(src_data)):
  11.     if src_data.iloc[i,0] != src_data.iloc[i-1,0]:
  12.         count += 1
  13. count
  14. #data_aim = src_data[src_data["match_id"] == "2023-wimbledon-1701"]
  15. data_aim = src_data.copy()
  16. def time_to_seconds(time_str):
  17.     # 将时间字符串转换为datetime对象
  18.     time_obj = datetime.strptime(time_str, "%H:%M:%S")
  19.     
  20.     # 创建一个基准时间（00:00:00）
  21.     base_time = datetime.strptime("00:00:00", "%H:%M:%S")
  22.     
  23.     # 计算时间差，即转换为时间戳
  24.     time_delta = time_obj - base_time
  25.     
  26.     # 获取总秒数
  27.     total_seconds = time_delta.total_seconds()
  28.     
  29.     return int(total_seconds)
  30. y_data_aim = []
  31. for i in data_aim["elapsed_time"].values:
  32.     y_data_aim.append(time_to_seconds(i))
  33. data_aim["point_victor"].values
  34. data_aim["server"].values
  35. len(data_aim["server"].values)
  36. from scipy.stats import pearsonr
  37. corr, p_value = pearsonr(data_aim["point_victor"].values, data_aim["server"].values)
  38. corr
  39. p_value
  40. import seaborn as sns
  41. from sklearn.metrics import confusion_matrix
  42. cm = confusion_matrix(data_aim["point_victor"].values, data_aim["server"].values)
  43. sns.heatmap(cm, annot=True, fmt="d", cmap="Blues")
  44. plt.show()
  45. (2452 + 2451) / 7284
  46. #data_aim = src_data[src_data["match_id"] == "2023-wimbledon-1701"]
  47. data_aim_1 = src_data[src_data["match_id"] == "2023-wimbledon-1701"]
  48. data_aim_1 = data_aim_1[data_aim_1["set_no"] == 1]
  49. len(data_aim_1['point_victor'])
  50. data_aim_1['point_victor'].values
  51. y_data_aim_1 = []
  52. for i in data_aim_1["elapsed_time"].values:
  53.     y_data_aim_1.append(time_to_seconds(i))
  54. plt.plot(data_aim_1["elapsed_time"].values,data_aim_1['point_victor'].values,'x')
  55. plt.xticks([])
  56. plt.show()
  57. # A/B指标
  58. def count_three_numbers(arr):
  59.     count_ones = 0
  60.     count_twos = 0
  61.     for i in range(len(arr) - 4):
  62.         sub_array = arr[i:i+5]
  63.         if sub_array.count(1) == 4:
  64.             count_ones += 1
  65.         elif sub_array.count(2) == 4:
  66.             count_twos += 1
  67.     return count_ones, count_twos
  68. count_three_numbers(list(data_aim_1['point_victor'].values))
  69. np.mean(data_aim["p1_distance_run"].values)
  70. np.mean(data_aim["p2_distance_run"].values)
  71. (14.002310680944536+13.869239017023613)/2
  72. t_data_aim = data_aim[data_aim["p1_distance_run"] > data_aim["p2_distance_run"]]
  73. len(t_data_aim[t_data_aim["point_victor"] == 1])
  74. run_cm = [[1612,2136],[2083,1612]]
  75. sns.heatmap(run_cm, annot=True, fmt="d", cmap="Blues")
  76. plt.show()
  77. (2136+2073)/len(data_aim)
  78. def count_run(pd_frame):
  79.     run_arvg = 13.94
  80.     d_now_run = pd_frame["p1_distance_run"] - pd_frame["p2_distance_run"]
  81.     if(np.abs(d_now_run) > run_arvg):
  82.         return -d_now_run/max(pd_frame["p1_distance_run"],pd_frame["p2_distance_run"])*0.2
  83.     return -(pd_frame["p1_distance_run"] - pd_frame["p2_distance_run"])/run_arvg*0.2
  84. data_aim_1_all = src_data[src_data["match_id"] == "2023-wimbledon-1301"]
  85. plt.plot(data_aim_1_all["p1_distance_run"])
  86. plt.plot(data_aim_1_all["p2_distance_run"])
  87. #p_dis = data_aim_1["p1_distance_run"]/data_aim_1["p2_distance_run"]
  88. plt.show()
  89. # A/B指标
  90. # 返回 1 或 -1
  91. def count_A_d_B_numbers(arr):
  92.     pass
  93. data_aim.columns
  94. def count_fault(pd_frame):
  95.     ans = 0
  96.     if pd_frame["p1_double_fault"]==1 or pd_frame["p1_unf_err"]==1:
  97.         ans = -1
  98.     elif pd_frame["p2_double_fault"]==1 or pd_frame["p2_unf_err"]==1:
  99.         ans = 1
  100.     return ans * 0.2
  101. data_aim.columns
  102. def count_sev(pd_frame):
  103.     ans = 0
  104.     if pd_frame["server"]==1:
  105.         ans = 1
  106.     elif pd_frame["server"]==2:
  107.         ans = -1
  108.     return ans * 0.2
  109. def count_win(pd_frame):
  110.     ans = 0
  111.     if pd_frame["p1_points_won"] > pd_frame["p2_points_won"]:
  112.         ans = 1
  113.     elif pd_frame["p1_points_won"] < pd_frame["p2_points_won"]:
  114.         ans = -1
  115.     return ans
  116. n_data_aim = src_data[src_data["match_id"] == "2023-wimbledon-1301"]
  117. n_data_aim
  118. other_index_run = np.zeros(len(n_data_aim))
  119. other_index_fault = np.zeros(len(n_data_aim))
  120. other_index_sev = np.zeros(len(n_data_aim))
  121. other_index_win = np.zeros(len(n_data_aim))
  122. other_index = np.zeros(len(n_data_aim))
  123. for i in range(len(n_data_aim)):
  124.     other_index_run[i] = count_run(n_data_aim.iloc[i])
  125.     other_index_fault[i] = count_fault(n_data_aim.iloc[i])
  126.     other_index_sev[i] = count_sev(n_data_aim.iloc[i])
  127.     other_index_win[i] = count_win(n_data_aim.iloc[i])
  128.     other_index[i] = other_index_run[i] + other_index_fault[i] + other_index_sev[i] #+ other_index_win[i]

2.2 问题二

2.2.1 问题二求解思路

针对该问题，可以通过两个方面来评估，得到“动量”在比赛中的确起作用的观点。通过可视化数据量化表示动量和比赛结果的单调关系，动态展示相关性。并在测试集上计算每步动量和比赛最终胜负的相关关系。通过仿真生成随机的得分方案，进行同样的相关性分析。

2.2.2 问题二模型建立与求解

首先计算从1301-1701一共31场比赛的积累动量，经计算共有4场不匹配，有效概率为87.1%

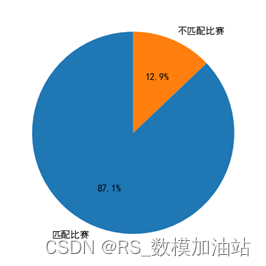
 其中不匹配的比赛分别为1304，1307，1404，1701，四场比赛几乎都比至最后一场，甚至在1304，1404场次都存在净胜场领先但是总场次落败的情况，在上述情况下基于动量的方式来进行比赛结果的判断容易发生混淆。

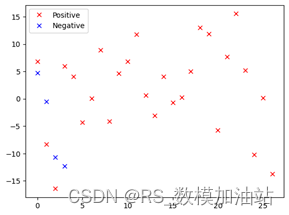
 使用卡方检验对原问题进行分析，即原假设为：运动员在比赛中发生的状态波动是随机的，与动量无关，则比赛胜负和积累动量的正负是相互独立的。

 卡方统计量为13.8 ，自由度为1，p值 为$2\times {​{10}^{-5}}<0.05$，可以拒绝原假设，从而判断动量在比赛中会起作用。

  1. from scipy.stats import ks_2samp
  2.  
  3. # 两个样本数据
  4. sample1 = [1, 2, 3, 4, 5]
  5. sample2 = [10, 4, 6, 8, 10]
  6.  
  7. # 进行KS检验
  8. statistic, p_value = ks_2samp(sample1, sample2)
  9.  
  10. # 输出结果
  11. print("KS统计量:", statistic)
  12. print("p值:", p_value)
  13.  
  14. import matplotlib.pyplot as plt
  15. import numpy as np
  16. import pandas as pd
  17. from datetime import datetime, timedelta
  18.  
  19. src_data = pd.read_csv("E:\\在写的东西\\24数模美赛\\Wimbledon_featured_matches.csv")
  20.  
  21. def time_to_seconds(time_str):
  22.     # 将时间字符串转换为datetime对象
  23.     time_obj = datetime.strptime(time_str, "%H:%M:%S")
  24.     
  25.     # 创建一个基准时间（00:00:00）
  26.     base_time = datetime.strptime("00:00:00", "%H:%M:%S")
  27.     
  28.     # 计算时间差，即转换为时间戳
  29.     time_delta = time_obj - base_time
  30.     
  31.     # 获取总秒数
  32.     total_seconds = time_delta.total_seconds()
  33.     
  34. return int(total_seconds)
  35.  
  36. def sliding_window_average(arr):
  37.     averages = []
  38.     for i in range(len(arr) - 2):
  39.         window_sum = arr[i] + arr[i + 1] +arr[i+2]
  40.         window_average = window_sum / 3.0
  41.         averages.append(window_average)
  42.     averages.append(arr[-2])
  43.     averages.append(arr[-1])  # 添加最后一个元素到新数组中
  44.     return averages
  45.  
  46. n_data_aim = src_data[src_data["match_id"] == "2023-wimbledon-1701"]
  47.  
  48. AB_array = count_three_numbers(list(n_data_aim["point_victor"].values))*0.4
  49.  
  50. other_index_run = np.zeros(len(n_data_aim))
  51. other_index_fault = np.zeros(len(n_data_aim))
  52. other_index_sev = np.zeros(len(n_data_aim))
  53. other_index_win = np.zeros(len(n_data_aim))
  54. other_index = np.zeros(len(n_data_aim))
  55.  
  56. for i in range(len(n_data_aim)):
  57.     other_index_run[i] = count_run(n_data_aim.iloc[i])
  58.     other_index_fault[i] = count_fault(n_data_aim.iloc[i])
  59.     other_index_sev[i] = count_sev(n_data_aim.iloc[i])
  60.     other_index_win[i] = count_win(n_data_aim.iloc[i])
  61.     other_index[i] = other_index_run[i] + other_index_fault[i] + other_index_sev[i]
  62.  
  63.

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/菜鸟追梦旅行/article/detail/141200?site
推荐阅读

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。