数据处理方法整理【目前最全】

数据处理方法

主要采用编写数据处理代码来对数据进行处理步骤，主要采用Python语言，使用相关的Pandas、Numpy、Scikit-learn等库来进行操作，一些代码实例如下。

1、缺失数据处理

数据缺失是指数据集中某行记录或某列特征的变量值存在空值的情况。常用的缺失值处理方法主要包括以下几种：
（1）删除法，若数据集中某行记录或某一列特征的数据缺失比率大于指定阅值时，可以认为该行数据或该列特征为无效数据或无效特征，直接删除含缺失数据的记录即可。

# 参考代码
# 缺失值进行判断
df.isnull()
# 缺失值删除
df.dropna(axis=0, how=‘any’, thresh=None, subset=None, inplace=False)
# pandas删除全为0值的行
df.drop( index = df.age[df1.age == 0].index )
# 参数：
# axis：轴。0或’index’，表示按行删除；1或’columns’，表示按列删除。
# how：筛选方式。‘any’，表示该行/列只要有一个以上的空值，就删除该行/列；‘all’，表示该行/列全部都为空值，就删除该行/列。
# thresh：非空元素最低数量。int型，默认为None。如果该行/列中，非空元素数量小于这个值，就删除该行/列。
# subset：子集。列表，元素为行或者列的索引。如果axis=0或者‘index’，subset中元素为列的索引；如果axis=1或者‘column’，subset中元素为行的索引。由subset限制的子区域，是判断是否删除该行/列的条件判断区域。
# inplace：是否原地替换。布尔值，默认为False。如果为True，则在原DataFrame上进行操作，返回值为None。
1
2
3
4
5
6
7
8
9
10
11
12
13

（2）基于统计学变量的填充法，这类方法需要根据特征的类型和分布情况决定采用哪种统计学变量进行填充。例如：特征是离散型的，可以直接通过众数对缺失值进行填充；特征是连续数值型并且数据分布比较均匀，可以采用平均数对缺失值进行填充，用全局变量或是属性的平均值来代替所有缺失数据；特征是连续数值型但分布倾斜，可以采用中位数进行填充等。

# 参考代码

# 方法一：直接用Pandas库
# 均值填补数据
data['空缺值所在列名'] =  data['空缺值所在列名'].fillna(data['空缺值所在列名'].mean())
catering_sale = "catering_sale.xls" 
# 众数填补数据
data['空缺值所在列名'] =  data['空缺值所在列名'].fillna(data['空缺值所在列名'].mode()[0])
catering_sale = "catering_sale.xls" 
# 中位数填补数据
data['空缺值所在列名'] =  data['空缺值所在列名'].fillna(data['空缺值所在列名'].median())
catering_sale = "catering_sale.xls" 
# 前一个数据填补数据
data['空缺值所在列名'] =  data['空缺值所在列名'].fillna(method='pad')
catering_sale = "catering_sale.xls" 
# 后一个数据填补数据
data['空缺值所在列名'] =  data['空缺值所在列名'].fillna(method='bfill')

# 方法二：计算平均值等，再进行填充
# 对‘column’列用平均值带替代缺失值NaN计算平均值
c = avg = 0
for ele in df['column']:
    if str(ele).isnumeric():
        c += 1
        avg += ele
avg /= c
 
# 替换缺失值
df = df.replace(to_replace="NaN",
                value=avg)
 
# 展示数据
df
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

（3）基于插值的填充法，这类方法主要是通过随机插值、拉格朗日插值、多项式插值等方法对缺失的变量值进行填充。例如：多项式插值法是通过构建多项式来拟合现有的数据，使得所有的样本数据都符合该多项式的分布，需要获取某个样本的缺失值时，通过求解该多项式来获得。

# 参考代码

# 使用库函数进行插值
# Scipy库中的interp1d函数可以实现一维数据的插值，包括线性插值、多项式曲线插值和邻近值插值。
# 定义x,y分别为数据的‘时间轴’和需要插补的‘列名’
x = data['time']
y = data['column']
# xnew构建新的完整的时间序列 = [1,2,3,...23]
xnew = np.linspace(1,23,num=23)
# 线性插值
f1 = interp1d(x,y,kind='linear') # kind替换不同的种类用不同方法进行插值，多项式曲线插值-‘cubic’，邻近值插值-‘nearest’
ynew1 = f1(xnew)

# 自定义函数进行插值
from scipy.interpolate import lagrange # 拉格朗日函数
data=pd.read_excel('data.xls')
# 自定义列向量插值函数
def ploy(s,n,k=6):
	y=s[list(range(n-k,n))+list(range(n+1,n+1+k))]#取数
	y=y[y.notnull()]
	return lagrange(y.index,list(y))(n)
for i in data.columns:
	for j in range(len(data)):
		if(data[i].isnull())[j]:
			data[i][j]=ploy(data[i],j)
data.to_excel('data_1.xls')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

（4）基于模型的填充法，这类方法是利用有监督的模型或者无监督的模型来实现缺失值的填充。例如：K近邻填充是利用聚类的方式来获得某个缺失样本邻近的若干个样本点，通过对这些样本点计算均值或加权平均来进行缺失值填充。

# 参考代码
# scikit-learn发布0.22版本中，新增的非常好用的缺失值插补方法：KNNImputer。基于KNN算法使得可以更便捷地处理缺失值，并且与直接用均值、中位数相比更为可靠。
from sklearn.impute import KNNImputer
# n_neighbors为选择“邻居”样本的个数，这里n_neighbors=2。
imputer = KNNImputer(n_neighbors=2)
imputer.fit_transform(data)

# IterativeImputer多变量缺失值填补-虑数据在高维空间中的整体分布情况，然后在对有缺失值的样本进行填充。
# IterativeImputer多变量缺失值填补方法
iterimp = IterativeImputer(random_state = 123)
oceandfiter = iterimp.fit_transform(oceandf)
# 获取填充后的变量-column为第5列
column = oceandfiter[:,4]

# MissForest缺失值填补-利用随机森林的思想，进行缺失值填充
# MissForest缺失值填补方法
forestimp = MissForest(n_estimators = 100,random_state = 123)
oceandfforest = forestimp.fit_transform(oceandf)
# 获取填充后的变量-column为第5列
column = oceandfforest[:,4]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

（5）热卡填充法，这类方法是在数据集中寻找与缺失样本最相似的样本点，并利用该最相似样本的变量值对缺失数据进行填充。问题关键是不同的问题可能会选用不同的标准来对相似进行判定，以及如何制定这个判定标准。该方法概念上很简单，且利用了数据间的关系来进行空值估计，但缺点在于难以定义相似标准，主观因素较多。

# 参考代码

def hot_deck_imputation（dataframe：pd.DataFrame）：
	from sklearn.impute import KNNImputer 
	hot_deck_imputer = KNNlmputer（n_neighbors=2，weights="uniform"）#虽然看着是用 KNN，但是参数固定：n neighbors=2
	new_df= hot_deck_imputer.fit_transform（dataframe）
	return new_df
1
2
3
4
5
6
7

（6）预测法，这类方法是用预测模型来预测每一个缺失数据。用已有数据作为训练样本来建立预测模型，预测缺失数据。该方法最大限度地利用已知的相关数据，是比较流行的缺失数据处理技术。

# 参考代码

# 一些采用ML或DL方法进行预测来对缺失值进行插补，如RNN方法
# 南开大学Yonghong Luo等人提出的用GAN来进行时间序列插值的算法-算法框架（E2GAN）（文章发表于NIPS 2018 和IJCAI 2019）
1. Luo, Yonghong, et al. "Multivariate time series imputation with generative adversarial networks."Advances in Neural Information Processing Systems. 2018.
2. Luo, Yonghong, et al. "E 2 GAN: end-to-end generative adversarial network for multivariate time series imputation."Proceedings of the 28th International Joint Conference on Artificial Intelligence. AAAl Press, 2019.
1
2
3
4
5
6

2、数据重采样

针对时序数据可采用数据重采样方法，将时间序列从一个频率转换至另一个频率的过程，它主要有两种实现方式，分别是降采样和升采样，降采样指将高频率的数据转换为低频率，升采样则与其恰好相反，将低频率数据转换到高频率。

对于一些高密度传感器，会在毫秒级别产生海量时序数据，因此对此类大量数据进行采样，将数据压缩到秒、分钟、小时等级别，来对数据进行压缩，较少数据量。

可采用Pandas 提供的 resample() 函数来实现数据的重采样。

# 参考代码

DataFrame.resample(rule, on='索引列名', axis=0, fill_method=None, label='left', closed='left')
# on：可以指定某一列使用resample，例如：例如：resample(‘3D’, on=’交易日期’).sum()
# axis=0：默认是纵轴，横轴设置axis=1
# fill_method = None：升采样时如何插值，比如‘ffill’（向上采样）、‘bfill’（向下采样）等
# label= ‘right’：在降采样时，如何设置聚合值的标签，例如，9：30-9：35会被标记成9：30还是9：35,默认9：35
# closed = ‘right’：在降采样时，各时间段的哪一段是闭合的，‘right’或‘left’，默认‘right’
# label=’left’, closed=’left’，建议统一设置成’left’
# rule的取值对应如下：
B	工作日频率
C	自定义工作日频率
D	日历日频率
W	每周频率
M	月末频率
SM	半月末频率（15日和月末）
BM	营业月末频率
CBM	自定义业务月末频率
MS	月初频率
SMS	半个月开始频率（第1次和第15次）
BMS	营业月开始频率
CBMS	自定义营业月开始频率
Q	四分之一端频率
BQ	业务季度末频率
QS	四分之一起始频率
BQS	业务季度开始频率
A	年终频率
BA	营业年末频率
AS	年份起始频率
BAS	业务年度开始频率
BH	营业时间频率
H	每小时频率
T	分钟频率
S	第二频率
L	毫秒
U	微秒
N	纳秒

data_h =data_index.resample('H').first()
data_h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

3、离群值处理

当数据中的某个数据点明显偏离于其他数据点的分布或者某个数据点明显区别于其他的数据点时，将其判定为离群点（异常值），对离群值可采用异常数据检测的方法，检测异常值并将其进行去除。

异常数据检测主要包括以下几种方法：
（1）基于统计分析的方法，通过特征的描述信息以及特征值范围来判断数据是否异常。例如，对于年龄特征，规约其值的范围是[0，200]，当出现了负数或者大于200的数，则判断为异常数据。
（2）基于密度的方法，通过离群点的局部密度显著低于大部分近邻点的特点进行判定，适用于非均匀的数据集。
（3）基于聚类的方法，一般正常的数据点呈现“物以类聚”的聚合形态，正常数据出现在密集的邻域周围，而异常点偏离较远，以此来对数据进行判定异常。
（4）基于树的方法，通过划分来判定异常。如孤立森林（Isolation Forest，iForest）被认为是最有效的异常检测方法之一，该方法是通过计算样本点的异常关联度分数来进行异常判定，若某样本得到的异常关联度分数较高，且大于阅值时可以判定其为异常。
（5）基于预测的方法，对时序数据根据其预测出来的时序曲线和真实的数据相比，来判定异常值的出现。

具体一些方法介绍如下：

（1） 基于统计分布的异常检测

数据分布模型可以通过估计概率分布的参数来创建。如果一个对象不能很好地同该模型拟合，即如果它很可能不服从该分布，则它是一个异常。

3σ-法则

假设一组检测数据只含有随机误差，对原始数据进行计算处理得到标准差，然后按一定的概率确定一个区间，认为误差超过这个区间的就属于异常值。

(μ−3σ,μ+3σ)区间内的概率为99.74。所以可以认为，当数据分布区间超过这个区间时，即可认为是异常数据。

假设数据集由一个正太分布产生，该分布可以用 N(μ,σ) 表示，其中 μ 是序列的均值，σ是序列的标准差，数据落在 (μ-3σ,μ+3σ) 之外的概率仅有0.27%，落在 (μ-4σ,μ+4σ) 之外的区域的概率仅有0.01%，可以根据对业务的理解和时序曲线，找到合适的K值用来作为不同级别的异常报警。

# 参考代码

#3-sigma识别异常值
def three_sigma(df_col): #df_col：DataFrame数据的某一列
    rule = (df_col.mean() - 3 * df_col.std() > df_col) | (df_col.mean() + 3 * df_col.std() < df_col)
    index = np.arange(df_col.shape[0])[rule]
    outrange = df_col.iloc[index]
    return outrange

# 另一种方式识别低值和高值
def three_sigma(s):
    mu, std = np.mean(s), np.std(s)
    lower, upper = mu-3*std, mu+3*std
    return lower, upper
1
2
3
4
5
6
7
8
9
10
11
12
13
14

Z-score

Z-score为标准分数，测量数据点和平均值的距离，若A与平均值相差2个标准差，Z-score为2。当把Z-score=3作为阈值去剔除异常点时，便相当于3sigma。

# 参考代码

def z_score(s):
  z_score = (s - np.mean(s)) / np.std(s)
  return z_score
1
2
3
4
5

MA滑动平均法

识别数据不规则性的最简单的方法是标记偏离分布的数据点，包括平均值、中值、分位数和模式。
假定异常数据点是偏离平均值的某个标准偏差，那么我们可以计算时间序列数据滑动窗口下的局部平均值，通过平均值来确定偏离程度。这被技术称为滑动平均法(moving average，MA)，旨在平滑短期波动并突出长期波动。滑动平均还包括累加移动平均、加权移动平均、指数加权移动平均、双指数平滑、三指数平滑等，在数学上，nn周期简单移动平均也可以定义为“低通滤波器”。

该方法有明显缺陷：数据中可能存在与异常行为类似的噪声数据，所以正常行为和异常行为之间的界限通常不明显；异常或正常的定义可能经常发生变化，基于移动平均值的阈值可能并不总是适用。

# 参考代码

# 简单移动平均线(Simple Moving Average，SMA)|加权移动平均(Weighted Moving Average，WMA)|指数加权移动平均(exponentially weighted moving average，EWMA)
# python pandas包中，对于ewma和sma有现成的实现方法，这里对于wma进行代码的编写处理
class WMA(object):
    """
    加权移动平均实现
    """
    def get_wma_weights(span, flag=True):
        """
        计算每个数值点的wma权重值
        """
        paras = range(1, span + 1)
        count = sum(paras)
        if flag:
            return [float(para) / count for para in paras]
        else:
            return [float(para) / count for para in paras][::-1]

    def get_wma_values(self, datas):
        """
        计算wma数值
        """
        wma_values = []
        wma_keys = datas.index
        for length in range(1, len(datas) + 1):
            wma_value = 0
            weights = self.get_wma_weights(length)
            for index, weight in zip(datas.index, weights):
                wma_value += datas[index] * weight
            wma_values.append(wma_value)
        return pd.Series(wma_values, wma_keys)
# 计算异常值
def calculate_variance(data, moving_average):
    variance = 0
    flag_list = moving_average.isnull()
    count = 0
    for index in range(len(data)):
        if flag_list[index]:
            count += 1
            continue
        variance += (data[index] - moving_average[index]) ** 2
    variance /= (len(data) - count)
    return variance
    
# ewma进行拟合
ewma_line = pd.ewma(data, span=4)
# 简单移动平均
sma_line = pd.rolling_mean(data, window=4)
# wma加权移动平均
wma_line = WMA().get_wma_values(data)


sma_var = calculate_variance(data, sma_line)
wma_var = calculate_variance(data, wma_line)
ewma_var = calculate_variance(data, ewma_line)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

boxplot箱型图（分位数异常检测）

箱型图，是一种用作显示一组数据分散情况资料的统计图。主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较，其绘制方法是：先找出一组数据的最大值、最小值、中位数和上下两个四分位数。通过不同分位数来划分异常值和疑似异常值。

IQR是第三四分位数减去第一四分位数，大于Q3+1.5IQR之外的数和小于Q1-1.5*IQR的值被认为是异常值。

# 参考代码

# 定义箱线图识别异常值函数
def box_plot(Ser):
    '''
    Ser：进行异常值分析的DataFrame的某一列
    '''
    Low = Ser.quantile(0.25)-1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    Up = Ser.quantile(0.75)+1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    index = (Ser< Low) | (Ser>Up)
    Outlier = Ser.loc[index]
    return(Outlier)

box_plot(df['counts']).head(8)


# 另一种形式识别低值和高值
def boxplot(s):
    q1, q3 = s.quantile(.25), s.quantile(.75)
    iqr = q3 - q1
    lower, upper = q1 - 1.5*iqr, q3 + 1.5*iqr
    return lower, upper
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

Grubbs异常检验

Grubbs测试是一种从样本中找出outlier的方法，所谓outlier，是指样本中偏离平均值过远的数据，他们有可能是极端情况下的正常数据，也有可能是测量过程中的错误数据。使用Grubbs测试需要总体是正态分布的。

算法流程：

①.样本从小到大排序
②.求样本的mean和std.dev [均值和标准差]
③.计算min/max与mean的差距，更大的那个为可疑值
④.求可疑值的z-score (standard score)，如果大于Grubbs临界值，那么就是outlier；
⑤.Grubbs临界值可以查表得到[它由两个值决定：检出水平α（越严格越小）、样本数量n]，排除outlier，对剩余序列循环做①-④步骤。
由于这里需要的是异常判定，只需要判断tail_avg是否outlier即可。

# 参考代码

# 使用grubbs对应的库直接调用
# 添加包 pip install outlier_utils==0.0.3
from outliers import smirnov_grubbs as grubbs
grubbs.test(data, alpha) # 默认双边检验
# https://github.com/c-bata/outlier-utils
1
2
3
4
5
6
7

（2） 基于密度的异常检测

基于密度的异常检测有一个先决条件，即正常的数据点呈现“物以类聚”的聚合形态，正常数据出现在密集的邻域周围，而异常点偏离较远。
对于这种场景，我们可以计算得分来评估最近的数据点集，这种得分可以使用Eucledian距离或其它的距离计算方法，具体情况需要根据数据类型来定：类别型或是数字型。

对象的密度估计(1)可以相对直接地计算，特别是当对象之间存在邻近性度量时，低密度区域中的对象相对远离近邻，可能被看作异常。一种更复杂的方法考虑到(2)数据集可能有不同密度区域这一事实，仅当一个点的局部密度显著地低于它的大部分近邻时才将其分类为离群点。

• 基于密度的异常分的计算公式：

$$\mathrm{density}(x,k)={\left(\frac{{\sum }_{y\in N(x,k)}\mathrm{distance}(x,y)}{|N(x,k)|}\right)}^{-1}$$

其中$N(x,k)$指的是x的k个最近的邻居的集合，$|N(x,k)|$表示该集合的大小，y是x最近的邻居。

LOF

局部异常因子算法，全称Local Outlier Factor（简写LOF)。LOF算法是一种无监督的异常检测方法，它计算给定数据点相对于其邻居的局部密度偏差。每个样本的异常分数称为局部异常因子。异常分数是局部的，取决于样本相对于周围邻域的隔离程度。确切地说，局部性由k近邻给出，并使用距离估计局部密度。通过将样本的局部密度与其邻居的局部密度进行比较，可以识别密度明显低于其邻居的样本,，这些样本就被当做是异常样本点。

数据点 $\mathrm{P}$ 的局部相对密度（局部异常因子）为点 $\mathrm{P}$ 邻域内点的平均局部可达密度跟数据点 的$\mathrm{P}$局部可达密度的比值, 即：
$$LO{F}_k(P)=\frac{{\sum }_{O\ni N_k(P)}\frac{\mathrm{lr}(O)}{\mathrm{lr}(P)}}{\left|N_k(P)\right|}=\frac{{\sum }_{O\ni N_k(P)}\mathrm{lrd}(O)}{\left|N_k(P)\right|}/\mathrm{lrd}(P)$$
数据点 $\mathrm{P}$ 的局部可达密度 $=\mathrm{P}$ 最近邻的平均可达距离的倒数。距离越大，密度越小。
$${\mathrm{lrd}}_k(P)=\frac{1}{\frac{{\sum }_{o\ni N_k(P)}\text{ reach }{}_{d}is{t}_k(P,O)}{|N_k(P)|}}$$
点 $\mathrm{P}$ 到点 $O$ 的第 $\mathrm{k}$ 可达距离 $=\max$ (点 $O$ 的 $\mathrm{k}$ 近邻距离，点 $\mathrm{P}$ 到点 $O$ 的距离)。
 reach  dist ⁡ k ( O , P ) = max ⁡ { d k ( O ) , d ( O , P ) } \text { reach } \operatorname{dist}_k(O, P)=\max \left\{d_k(O), d(O, P)\right\}  reach distk​(O,P)=max{dk​(O),d(O,P)}

点 $O$ 的 $k$ 近邻距离=第 $k$ 个最近的点跟点 $O$ 之间的距离。

整体来说，LOF算法流程如下：

• 对于每个数据点，计算它与其他所有点的距离，并按从近到远排序；
• 对于每个数据点，找到它的 K-Nearest-Neighbor，计算LOF得分。

# 参考代码
from sklearn.neighbors import LocalOutlierFactor as LOF

clf = LOF(n_neighbors=2)
res = clf.fit_predict(data)
print(res)
print(clf.negative_outlier_factor_)
1
2
3
4
5
6
7

COF

COF是LOF的变种，相比于LOF，COF可以处理低密度下的异常值，COF的局部密度是基于平均链式距离计算得到。在开始时一样会先计算出每个点的k-nearest neighbor。而接下来会计算每个点的Set based nearest Path，如下图：

假使k=5，所以F的neighbor为B、C、D、E、G。而对于F离他最近的点为E，所以SBN Path的第一个元素是F、第二个是E。离E最近的点为D所以第三个元素为D，接下来离D最近的点为C和G，所以第四和五个元素为C和G，最后离C最近的点为B，第六个元素为B。所以整个流程下来，F的SBN Path为{F, E, D, C, G, C, B}。而对于SBN Path所对应的距离e={e1, e2, e3,…,ek}，依照上面的例子e={3,2,1,1,1}。
所以可以说假使想计算p点的SBN Path，只要直接计算p点和其neighbor所有点所构成的graph的minimum spanning tree，之后再以p点为起点执行shortest path算法，就可以得到SBN Path。而接下来有了SBN Path，就会接着计算p点的链式距离:
$${\mathrm{a}\mathrm{c}}_{-}\mathrm{dist}(p)=\sum _{i=1}^k\frac{2(k+1-i)}{k(k+1)}\mathrm{dist}\left(e_i\right)$$
有了ac_distance后，就可以计算COF:
$$\mathrm{COF}(p)=\frac{a{c}_{-}\mathrm{dist}(p)}{\frac{1}{k}{\sum }_{o\in N_k(p)}a{c}_{-}\mathrm{dist}(o)}$$

# 参考代码

from pyod.models.cof import COF
cof = COF(contamination = 0.06,  ## 异常值所占的比例
          n_neighbors = 20,      ## 近邻数量
        )
cof_label = cof.fit_predict(iris.values) # 鸢尾花数据
print("检测出的异常值数量为:",np.sum(cof_label == 1))
1
2
3
4
5
6
7
8

（3）基于聚类的异常检测

通常，类似的数据点往往属于相似的组或簇，由它们与局部簇心的距离决定。正常数据距离簇中心的距离要进，而异常数据要远离簇的中心点。聚类属于无监督学习领域中最受欢迎的算法之一，关于聚类异常检测可分为两步：

①利用聚类算法聚类;
②计算各个样本点的异常程度：每个点的异常程度等于到最近类中心点的距离。

• 方法一：丢弃远离其他簇的小簇。
  这种方法可以与任何聚类方法一起使用，但是需要最小簇大小和小簇与其他簇之间距离的國值。通常，该过程可以简化为丢弃小于某个最小尺寸的所有簇。这种方案对簇个数的选择高度敏感。此外，这一方案很难将离群点得分附加在对象上。注意，把一组对像看作离群点，将离群点的概念从个体对象扩展到对象组，但是本质上没有任何改变。
• 方法二：聚类所有对象，然后评估对象属于簇的程度。
  • 对于基于原型的聚类，可以用对象到它的簇中心的距离来度量对象属于簇的程度。
  • 对于基于目标函数的聚类方法，可以使用该目标函数来评估对象属于任意簇的程度。
    特殊情况下，如果删除一个对象导致该目标的显著改进，则我们可以将对象分类为离群点。比如，对于K均值，删除远离其相关簇中心的对象能够显著地改进簇的误差的平方和（SSE）。

总而言之，聚类创建数据的模型，而非异常扭曲模型。

K-Means聚类

创建了k个类似的数据点群体，不属于这些簇（远离簇心）的数据样例则有可能被标记为异常数据。

# 参考代码

# 用不同数量的质心计算-这里划分20个聚类
n_cluster = range(1, 20)
kmeans = [KMeans(n_clusters=i).fit(data) for i in n_cluster]
scores = [kmeans[i].score(data) for i in range(len(kmeans))]
# 这里选择15个质心并将这些数据添加到中心数据框中
df['cluster'] = kmeans[14].predict(data)

# 获取每个点与其最近的质心之间的距离。 最大距离被视为异常
distance = getDistanceByPoint(data, kmeans[14])
# 异常点的数量
number_of_outliers = int(outliers_fraction*len(distance))
# 异常判定的阈值，大于阈值判定为异常
threshold = distance.nlargest(number_of_outliers).min()
# anomaly21 包含异常结果，0为正常，1为异常
df['anomaly21'] = (distance >= threshold).astype(int)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

DBSCAN

通过聚类时可以找出异常点

• 1个核心思想：基于密度
  DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。

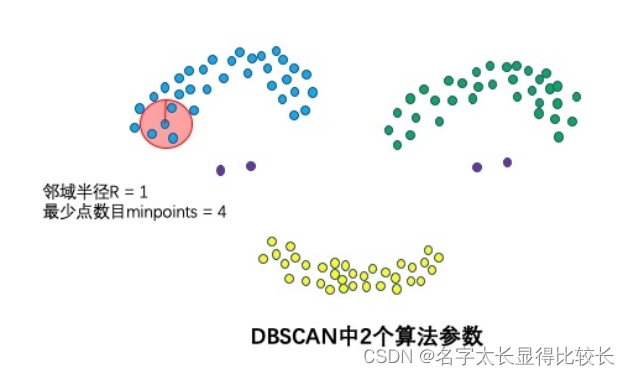
• 2个算法参数：邻域半径R和最少点数目minpoints
  刻画密集 —> 当邻域半径R内的点的个数大于最少点数目minpoints时，就是密集。
  

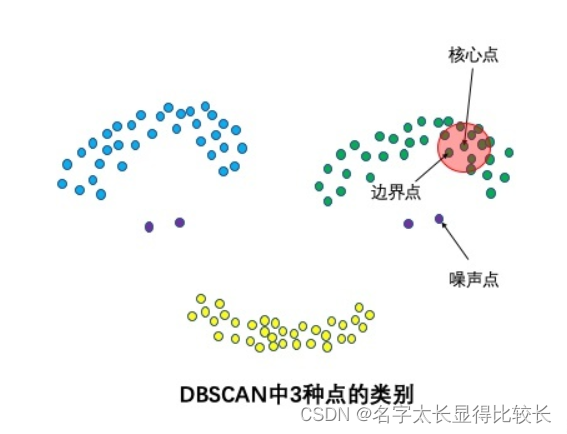
• 3种点类别：核心点，边界点和噪声点
  核心点：邻域半径R内样本点的数量大于等于minpoints的点叫做核心点。
  边界点：不属于核心点但在某个核心点的邻域内的点叫做边界点。
  噪声点：既不是核心点也不是边界点的是噪声点。
  

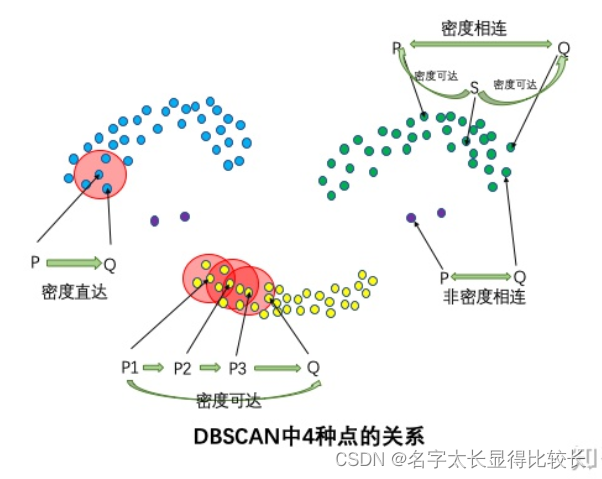
• 4种点的关系：密度直达，密度可达，密度相连，非密度相连
  密度直达：如果P为核心点，Q在P的R邻域内，那么称P到Q密度直达。任何核心点到其自身密度直达，密度直达不具有对称性，如果P到Q密度直达，那么Q到P不一定密度直达。
  密度可达：如果存在核心点P2，P3，……，Pn，且P1到P2密度直达，P2到P3密度直达，……，P(n-1)到Pn密度直达，Pn到Q密度直达，则P1到Q密度可达。密度可达也不具有对称性。
  密度相连：如果存在核心点S，使得S到P和Q都密度可达，则P和Q密度相连。密度相连具有对称性，如果P和Q密度相连，那么Q和P也一定密度相连。密度相连的两个点属于同一个聚类簇。
  非密度相连：如果两个点不属于密度相连关系，则两个点非密度相连。非密度相连的两个点属于不同的聚类簇，或者其中存在噪声点。
  

判断异常与 k-means 算法一致，在聚类时可以找出异常点。但不需要输入簇数 k 而且可以发现任意形状的聚类簇。

# 参考代码

# 直接使用sklearn库中的DBSCAN即可
from sklearn.cluster import DBSCAN
import numpy as np
X = np.array([[1, 2], [2, 2], [2, 3],
              [8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)

clustering.labels_
array([ 0,  0,  0,  1,  1, -1])
# 0，,0，,0：表示前三个样本被分为了一个群
# 1, 1：中间两个被分为一个群
# -1：最后一个为异常点，不属于任何一个群
1
2
3
4
5
6
7
8
9
10
11
12
13
14

（4）基于树的异常检测

这类方法为基于划分的方法范畴。

最简单的划分方法就是阈值检测，其通过人为经验划定阈值，对数据进行异常判断。
具体的，为了避免单点抖动产生的误报，需要将求取累积的窗口均值进行阈值判别，具体的累积就是通过窗口进行操作：
$$\hat{x}(t)=\frac{x_t+x_{t-1}+\dots +x_{t-w+1}}{w}$$
高级的基于划分的异常检测算法，是iForest （Isolation Forest）孤立森林，一个基于Ensemble的快速异常检测方法，具有线性时间复杂度和高精准度。与LOF、OneClassSVM相比，其占用的内存更小、速度更快。算法原理如下： 其将时序中的数据点划分成树，深度越低，说明越容易被划分，即为离群点。
算法不借助类似距离、密度等指标去描述样本与其他样本的差异，而是直接去刻画所谓的疏离程度(isolation)。假设现在有一组一维数据，我们要对这组数据进行切分，目的是把点A和 B单独切分出来，先在最大值和最小值之间随机选择一个值 X，然后按照 <X 和 >=X 可以把数据分成左右两组，在这两组数据中分别重复这个步骤，直到数据不可再分。一些密度很高的簇要被切很多次才会停止切割，即每个点都单独存在于一个子空间内，但那些分布稀疏的点，大都很早就停到一个子空间内了。所以实现孤立森林的异常检测。

# 参考代码

from sklearn.datasets import load_iris 
from sklearn.ensemble import IsolationForest

data = load_iris(as_frame=True) 
X,y = data.data,data.target 
df = data.frame 

# 模型训练
iforest = IsolationForest(n_estimators=100, max_samples='auto',  
                          contamination=0.05, max_features=4,  
                          bootstrap=False, n_jobs=-1, random_state=1)

#  fit_predict 函数 训练和预测一起 可以得到模型是否异常的判断，-1为异常，1为正常
df['label'] = iforest.fit_predict(X) 

# 预测 decision_function 可以得出 异常评分
df['scores'] = iforest.decision_function(X)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

（5）基于降维的异常检测

PCA

PCA[线性方法]在做特征值分解之后得到的特征向量反应了原始数据方差变化程度的不同方向，特征值为数据在对应方向上的方差大小。所以，最大特征值对应的特征向量为数据方差最大的方向，最小特征值对应的特征向量为数据方差最小的方向。原始数据在不同方向上的方差变化反应了其内在特点。如果单个数据样本跟整体数据样本表现出的特点不太一致，比如在某些方向上跟其它数据样本偏离较大，可能就表示该数据样本是一个异常点。

• PCA一种方法就是找到k个特征向量，并计算每个样本再经过这k个特征向量投射后的重建误差（reconstruction error），而正常点的重建误差应该小于异常点。
• 同理，也可以计算每个样本到这k个选特征向量所构成的超空间的加权欧氏距离（特征值越小权重越大）。
• 也可以直接对协方差矩阵进行分析，并把样本的马氏距离（在考虑特征间关系时样本到分布中心的距离）作为样本的异常度，而这种方法也可以被理解为一种软性（Soft PCA）

# 参考代码

from sklearn.decomposition import PCA
pca = PCA()
pca.fit(centered_training_data)
transformed_data = pca.transform(training_data)
y = transformed_data

# 计算异常分数
lambdas = pca.singular_values_
M = ((y*y)/lambdas)

# 前k个特征向量和后r个特征向量
q = 5
print "Explained variance by first q terms: ", sum(pca.explained_variance_ratio_[:q])
q_values = list(pca.singular_values_ < .2)
r = q_values.index(True)

# 对每个样本点进行距离求和的计算
major_components = M[:,range(q)]
minor_components = M[:,range(r, len(features))]
major_components = np.sum(major_components, axis=1)
minor_components = np.sum(minor_components, axis=1)

# 人为设定c1、c2阈值
components = pd.DataFrame({'major_components': major_components, 
                               'minor_components': minor_components})
c1 = components.quantile(0.99)['major_components']
c2 = components.quantile(0.99)['minor_components']

# 制作分类器
def classifier(major_components, minor_components):  
    major = major_components > c1
    minor = minor_components > c2    
    return np.logical_or(major,minor)

results = classifier(major_components=major_components, minor_components=minor_components)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

Autoencoder

由于PCA 方法的线性使得特征维度类型的抽取上有很大限制。近年来很多神经网络的方法被用于时间序列的异常检测，比如Autoencoder，通过引入神经网络天生的非线性性克服这些限制。

Auto-Encoder，中文称作自编码器，是一种无监督式学习模型。它基于反向传播算法与最优化方法（如梯度下降法），利用输入数据$X$本身作为监督，来指导神经网络尝试学习一个映射关系，从而得到一个重构输出$X^R$。在时间序列异常检测场景下，异常对于正常来说是少数，所以我们认为，如果使用自编码器重构出来的输出$X^R$跟原始输入的差异超出一定阈值（threshold）的话，原始时间序列即存在了异常。[如果样本都是数值型，可以用MSE或MAE作为衡量指标，样本的重建误差越大，则表明异常的可能性越大]

算法模型包含两个主要的部分：Encoder（编码器）和Decoder（解码器）。

编码器的作用是把高维输入$X$编码成低维的隐变量$h$从而强迫神经网络学习最有信息量的特征；解码器的作用是把隐藏层的隐变量$h$还原到初始维度，最好的状态就是解码器的输出能够完美地或者近似恢复出原来的输入, 即$X^R ≈ X $ 。

# 参考代码

import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense

# 标准化数据
scaler = preprocessing.MinMaxScaler()
X_train = pd.DataFrame(scaler.fit_transform(dataset_train),
                              columns=dataset_train.columns,
                              index=dataset_train.index)
# Random shuffle training data
X_train.sample(frac=1)
X_test = pd.DataFrame(scaler.transform(dataset_test),
                             columns=dataset_test.columns,
                             index=dataset_test.index)

tf.random.set_seed(10)
act_func = 'relu'
# Input layer:
model=Sequential()
# First hidden layer, connected to input vector X.
model.add(Dense(10,activation=act_func,
                kernel_initializer='glorot_uniform',
                kernel_regularizer=regularizers.l2(0.0),
                input_shape=(X_train.shape[1],)
               )
         )
model.add(Dense(2,activation=act_func,
                kernel_initializer='glorot_uniform'))
model.add(Dense(10,activation=act_func,
                kernel_initializer='glorot_uniform'))
model.add(Dense(X_train.shape[1],
                kernel_initializer='glorot_uniform'))
model.compile(loss='mse',optimizer='adam')
print(model.summary())

# Train model for 100 epochs, batch size of 10:
NUM_EPOCHS=100
BATCH_SIZE=10
history=model.fit(np.array(X_train),np.array(X_train),
                  batch_size=BATCH_SIZE,
                  epochs=NUM_EPOCHS,
                  validation_split=0.05,
                  verbose = 1)

plt.plot(history.history['loss'],
         'b',
         label='Training loss')
plt.plot(history.history['val_loss'],
         'r',
         label='Validation loss')
plt.legend(loc='upper right')
plt.xlabel('Epochs')
plt.ylabel('Loss, [mse]')
plt.ylim([0,.1])
plt.show()

# 查看训练集还原的误差分布如何，以便制定正常的误差分布范围
X_pred = model.predict(np.array(X_train))
X_pred = pd.DataFrame(X_pred,
                      columns=X_train.columns)
X_pred.index = X_train.index

scored = pd.DataFrame(index=X_train.index)
scored['Loss_mae'] = np.mean(np.abs(X_pred-X_train), axis = 1)
plt.figure()
sns.distplot(scored['Loss_mae'],
             bins = 10,
             kde= True,
            color = 'blue')
plt.xlim([0.0,.5])

# 误差阈值比对，找出异常值
X_pred = model.predict(np.array(X_test))
X_pred = pd.DataFrame(X_pred,
                      columns=X_test.columns)
X_pred.index = X_test.index
threshod = 0.3
scored = pd.DataFrame(index=X_test.index)
scored['Loss_mae'] = np.mean(np.abs(X_pred-X_test), axis = 1)
scored['Threshold'] = threshod
scored['Anomaly'] = scored['Loss_mae'] > scored['Threshold']
scored.head()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

（6）基于分类的异常检测

OneClassSVM

SVM（支持向量机）是一种用于检测异常的有效的技术。SVM通常与监督学习相关联，是一类对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。

但是存在可以用于将异常识别为无监督问题（其中训练数据未被标记）的扩展（OneClassCVM）。算法学习软边界以便使用训练集对正常数据实例进行聚类，然后，使用测试实例，通过调整自身以识别落在学习区域之外的异常。根据使用情况，异常检测器的输出可以是数字标量值，用于过滤特定于域的阈值或文本标签（如二进制/多标签）。

One-Class SVM 是基于一类数据（正常数据）求超平面，对 SVM 算法中求解负样本最大间隔目标进行改造，进而完成非监督学习下的异常检测。可以理解为这是一个新颖值检测(Novelty Detection)算法，即在One-Class SVM 将所以与正常数据有一定区别的都当成新颖数据，而我们根据实际需要设定边界，才认为超出边界的数据为异常数据。

# 参考代码

from sklearn import svm
# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel='rbf', gamma=0.1)
clf.fit(X)
y_pred = clf.predict(X)
# 输出异常值
n_error_outlier = y_pred[y_pred == -1].size
1
2
3
4
5
6
7
8
9

（7）基于预测的异常检测

对于单条时序数据，根据其预测出来的时序曲线和真实的数据相比，求出每个点的残差，并对残差序列建模，利用KSigma或者分位数等方法便可以进行异常检测。具体的流程如下：

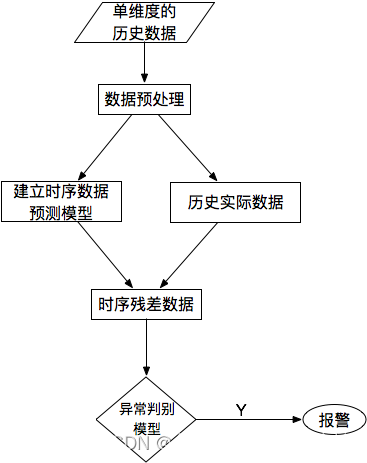
数据融合处理

将多维传感器产生的数据进行数据融合，能够产生比单一信息源更精确、更完全、更可靠的数据。数据融合分为预处理和数据融合两步。

1. 预处理
   1）外部校正，去除外部地形、天气、气压、风速等外部噪声引起的对结果数据的影响，外部校正的目的主要在于去除外部随机因素对测量数据结果一致性的影响。
   2）内部校正，去除由于各个传感器灵敏度、分辨率等自身参数差异引起的对结果数据的影响，内部校正的目的主要在于消除由不同传感器得到的数据差异。

2. 数据融合
   根据不同的数据融合目的及数据融合所处层次，选择恰当的数据融合算法，将提取的特征或多维数据进行合成，得到比单一传感器更准确的表示或估计。

根据数据融合的操作对象级别从高到低分为：决策级融合、特征级融合及数据级融合。

1）数据级融合
操作对象是最前端的数据，对传感器采集到的原始数据进行处理，是最底层的融合。常用的数据级数据融合方法有：小波变换法、代数法、坎斯-托马斯变换（Kauth-Thomas Transformation，K-T）等。

2）特征级的数据融合
特征级数据融合面向监测对象特征的融合，从传感器采集到的原始数据中提取特征信息，用以反映事物的属性，以便进行综合分析和处理，是数据融合的中间环节。
特征级数据融合一般流程为：首先对数据进行预处理，然后对数据进行特征提取，再对特征提取后的数据进行特征级融合，最后对融合后的数据属性进行说明。

3）决策级数据融合
在底层两级数据融合的基础上，对数据进行特征提取、数据分类及逻辑运算，为管理者决策提供辅助。所需的决策是最高级的数据融合。该级别数据融合的特点是容错性、实时性好，当一个或几个传感器失效时，仍能做出决策。
决策级数据融合一般流程为：对数据进行预处理，然后对数据进行特征提取，再对特征进行属性说明，对属性进行融合，最后对融合属性进行说明。

通过不同的融合操作来对多传感器测量数据进行数据合并，减少存储数据量，降低数据分辨率，但同时也能呈现出融合后数据保留所需的全部信息。

# 参考代码

# 这里简单介绍对多个传感器测量一个特征的数据采用‘卡尔曼滤波’来进行 数据融合

# 卡尔曼增益 = 数据1的误差 除以 (数据1的误差 + 数据2的误差)
# 误差对应方差
def kalman_gain(e1, e2):
    return e1/(e1 + e2)
 
# 估计值 = 数据1的估计值 + 系数*(数据2测量值 - 数据1的估计值)
def now_estimated_value(X1, K, X2):
    return X1 + K(X2 - X1)
 
# 更新估计误差 = （1 - 卡尔曼增益）* 数据1的估计误差 + 卡尔曼增益* 数据2的估计误差
def now_estimated_error(K, e1, e2):
    return (1 - K)*e1 + K*e2
 
# 循环体
K = kalman_gain(e1, e2)
X_k = now_estimated_value(X1, K, X2)
e_EST = now_estimated_error(K, e1, e2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

数据降维处理

对多个变量的大数据分析时，会有很多丰富信息，变量之间可能存在相关性，但增加了问题分析的复杂性。 而将每个指标进行分析，分析往往是孤立的，不能完全利用数据中的信息，因此盲目减少指标会损失很多有用的信息，甚至还可能产生错误的结论。

考虑将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。使得在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。

PCA 分析

主成分分析法 (Principal Componet Analysis, PCA）本质是通过某种线性映射，将高维数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此达到用较少的数据维度来保留较多的原数据点特性的效果。主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。 之后，可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

在计算上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。

# 参考代码

# 直接调用sklearn库中PCA
# X_new为标准化后的数据
from sklearn.decomposition import PCA
pca = PCA(n_components=2) # 设置PCA模型的参数n_components为2，即将三维数据降为二维数据
pca.fit(X_new) # 对标准化后的数据进行模型训练
X_transformed = pca.transform(X_new) # 对标准化后的数据进行降维
print(X_transformed)
print(pca.components_) # 获取线性组合系数
1
2
3
4
5
6
7
8
9
10

数据标准化

数据标准化是指通过一定的方法和比例将数据映射到指定区间，根据使用函数的不同可以归纳为三类：直线型无量纲法、折线形无量纲法以及曲线型无量纲法。一些原始数据集是没有经过转化的有量纲数据，如果将其直接输入到模型中进行训练，受不同量纲特征的影响，会导致模型的收敛速度变慢，并且当特征量纲级别相差特别大时，模型可能会忽略掉量纲较小的特征而达不到理想效果。因此，在模型训练前，需要通过标准化方法将数据转换成无量纲数据，以消除量纲对模型产生的影响。常见的标准化方法有如下几种：

（1）min-max标准化（归一化）：该方法是基于样本中的两个最值进行转换的，把最大值归为1，最小值归为0，其他值在其中分布。对于每个属性，设minA和maxA分别为属性A的最小值和最大值，将A的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x’，其公式为：新数据=(原数据 - 最小值)/(最大值 - 最小值)
$$X_{nev}=\frac{X-X_{\min }}{X_{\max }-X_{\min }}$$

# 参考代码

from sklearn import preprocessing
# feature_range设置最大最小变换值，默认（0,1）
min_max_normalizer=preprocessing.MinMaxScaler(feature_range=(0,1))
# 将数据缩放(映射)到设置固定区间
scaled_data=min_max_normalizer.fit_transform(data)
# 将变换后的数据转换为dataframe对象
price_frame_normalized=pandas.DataFrame(scaled_data)
1
2
3
4
5
6
7
8
9

（2）z-score标准化（规范化）：一般把均值归一化为0，方差归一化1。基于原始数据的均值（mean）和标准差（standarddeviation）进行数据的标准化。将A的原始值x使用z-score标准化到x’。z-score标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况，其公式为：新数据=(原数据-均值)/标准差
$$X_{\text{new }}=\frac{X-\mu }{\sigma }$$

# 参考代码

from sklearn import preprocessing
# Z-Score标准化
zscore_scaler=preprocessing.StandardScaler()
data_scaler_1=zscore_scaler.fit_transform(data)
1
2
3
4
5
6

（3）正则化：数据正则化是将样本的某个范数（如L1范数）缩放到到位1，正则化的过程是针对单个样本的，对于每个样本将样本缩放到单位范数。

# 参考代码

def proportional_normalization(value):
    """比例归一
    公式：值/总和
    return 值域[0,1]
    """
    new_value = value / value.sum()
    return new_value
1
2
3
4
5
6
7
8
9

（4）$\log$ 对数转换: 该方法是将满足特定条件的样本序列通过对数函数进行转换，其计算公式下所示。
$$X_{\text{new }}=\frac{{\log }_{10}X}{{\log }_{10}{X}_{\text{max }}}$$
​ 其中, X = { x 1 , x 2 , ⋯   , x i , ⋯   , x n } X=\left\{x_1, x_2, \cdots, x_i, \cdots, x_n\right\} X={x1​,x2​,⋯,xi​,⋯,xn​} 代表原始特征序列, 且需要满足 $x_i\ge 1$ 。

# 参考代码

def log_transfer(value):
    """log转换，需要原始数据都大于1
    公式：log10(x)/log10(max)
    return 值域[0,1]
    """
    new_value = np.log10(value) / np.log10(value.max())
    return new_value
1
2
3
4
5
6
7
8
9

（5）logistic 函数变换: 该方法是利用 Sigmoid 函数对数据进行转换, 其计算公式如下所示。
$$X_{n\text{ new }}=\frac{1}{1+e^{-x}}$$

# 参考代码

def sigmoid(value):
    """logistic转换，定义Sigmoid函数
    new_value = 1.0/(1+np.exp(-value))
    return new_value
1
2
3
4
5
6

特征工程

特征工程是指通过对原始数据进行分析与转换以获取对目标任务更好的表达，它是构造一个优秀模型的必要环节。因此，在经过数据预处理后，还需要通过一系列的特征工程方法对数据进行分析处理，挖掘其中的关键信息，来提升模型的稳定性和鲁棒性。常用的特征工程方法主要包括特征编码、相关性分析、特征筛选等。

1、特征编码

1. one-hot编码
   one-hot编码是常用的编码方式之一，它可以将类别特征映射成只包含0和1的维向量进行输出。假设类别型特征共有n个不同的类别，进行编码前需要根据类别数量建立一个n维词表，在对词表中第i个类别进行one-hot编码时，会输出一个n维的特征向量，该向量中位置i的值为1，其余位置的值均为0。one-hot编码虽然简单易用，但它无法处理类别间具有的关联性，这在一定程度上会影响模型对参数的拟合，并且当类别数量巨大时，还会使编码后的数据变得十分稀疏，导致模型训练速度变慢、效果变差。
   

2. Word2vec编码
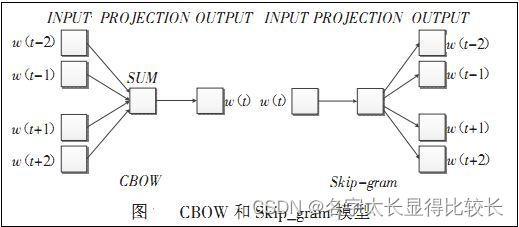
   Word2vec编码最先出现在 NLP（Natural Language Processing）领域，因为其效果好，被广泛引入到其他领域进行使用。Word2vec编码克服了one-hot编码的缺点，通过Word2vec编码可以将类别型特征映射成具有上下文关联性的向量，并且该向量也具有固定大小，不会形成稀疏矩阵。Word2vec是基于CBOW（Continuous Bag-of-Words Model）和Skip-Gram模型进行编码。通过Word2vec编码的每个嵌入向量会在模型训练时进行自动更新以获得最好的上下文关联性表达，当模型训练结束后可以获得固定的编码向量。
   

2、特性相关性分析

一般数据特征间具有一定程度的线性和非线性关联关系，传统模型如SVM、LR等是难以学习到特征间的这些相关性。因此需要通过辅助方法对特征的相关性进行分析，根据分析结果，再结合相关领域的知识以及对业务问题的专业理解，通过特征组合、特征交叉或者加减乘除的方式去构建出更能描述目标问题的关键特征。常见的特征相关性分析方法主要有：Pearson相关性系数、最大互信息系数。

1. Pearson 相关性系数
   Pearson相关性系数可用于衡量两个特征间线性相关程度。假设数据集中存在两个特征变量X =（x1，x2，…，xn）和Y=（y1，y2，…，yn），通过公式可以计算出X和Y的Pearson系数，该公式输出结果的范围在[-1，1]之间，零表示线性无关，正数表示正相关，负数表示负相关，并且Pearson系数的绝对值越大，两特征的相关程度就越高。
   $$r=\frac{{\sum }_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{{\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y_i-\bar{y}\right)}^2}}$$

​ 其中，$x_i$ 和 $y_i$ 表示数据集的第 $i$ 个样本中特征变量 $X$ 和 $Y$ 对应的取值，$\bar{x}$ 和 $\bar{y}$ 表示特征变量 $X$ 和 $Y$ 的均值，$n$ 表示样本数量。

2. 最大互信息系数
   最大互信息系数（MIC）可用于衡量两个特征间的线性或非线性关联程度，并且MIC值越大，两个特征的相关程度越高，其计算公式如下。MIC的具体思想如下：首先，根据两个特征的值以散点图的方式将数据点散落到二维平面中；接着，根据指定的网格分辨率对平面进行网格化，计算该网格分辨率下不同划分方式的最大互信息值，并进行归一化；最后，求出各网格分辨率中互信息的最大值作为MIC值。
   $$\mathrm{MIC}(D)=\underset{a\times b<B(n)}{\max }\frac{I(a\times b,X,Y)}{\log (\min (a,b))}$$

​ 其中，$I(a\times b,X,Y)$表示在格分辨率 $a\times b$ 下特征变量 $X$ 和 $Y$ 的最大互信息值，$\log (\min (a,b))$ 表示归一化因子，$B(n)$ 表示最大的网格分辨率。

3、特征选择

结合领域专业知识和相关任务要求对高维特征进行特征的筛选，可以选出需要的特征来进行后续模型的训练等步骤。常用的特征筛选方法有：
（1）方差选择法：该方法是通过计算每一列特征的方差，并根据设定的阅值来判段是否需要保留或者删除特征变量。如果某一列特征的方差很小，那么认为该列特征中所有数据几乎是没有变化的，这些无变化的数据对模型的训练没有任何意义，因此需要进行删除。
（2）树模型选择法：该方法是基于树模型（如XGBoost，RF）来进行特征选择，通过计算信息增益来给每个特征的重要度进行打分，从而可以选择出重要性高的特征、
（3）递归特征消除法：该方法通过选择一个基模型（如SVM、LR），并利用数据集对其进行多轮训练，每轮训练结束后，删除权重较低的特征，再进入下一轮次的训练，重复这个过程，直到剩余的特征数量与预先设定的特征数量一致。