进制转换:二,八,十,十六进制互相转换(含小数部分)超级详细_二进制转十六进制例题

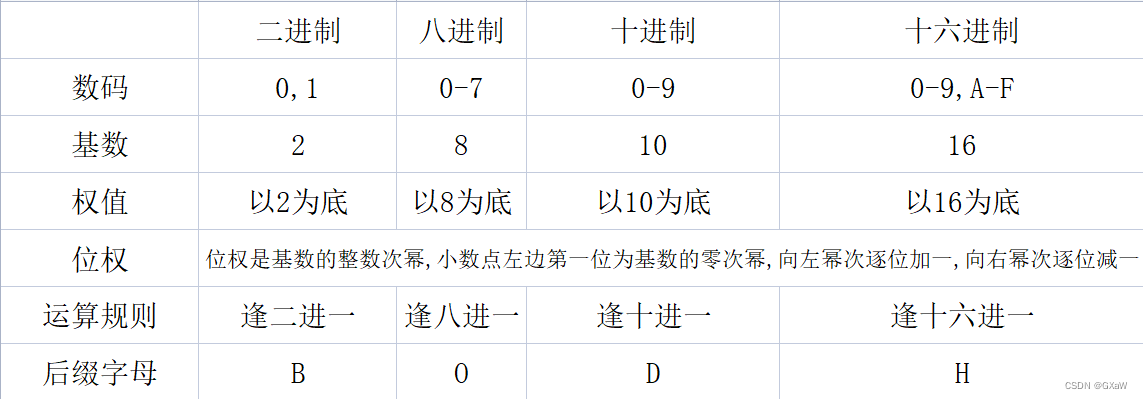
一些有用的概念

1.进位计数制:用进位的方法进行计数的数制,简称进制

2.数码:一组用来表示某种数制的符号. 如:0,1,2,3,4,A,B,C,D等

例如:二进制的数码是:0,1  基为2    八进制的数码是:0,1,2......7   基为8   

3.基数:数制所使用的数码个数称为"基数"或"基",常用字母 R表示,称为R进制.

4.位权:指数码在不同位置上的权值

 

二进制转十进制:

方法:按权展开

例题1:   1011.011转化为十进制是多少?

解析:

以小数点为分界线 .. 5   4    3   2    1    0  .  -1   -2    -3    -4..

 小数点左边 从0开始往左依次增加   小数点右边从-1开始向右依次减小

           1    0    1    1    .    0     1     1

           3    2    1    0         -1     -2    -3

解 :  1*2^0 + 1*2^1 + 0*2^2 + 1*2^3  +  0*2^(-1)  + 1*2^(-2)  +  1*2^(-3)

=   1      +   2     +    0    +    8      +      0        +    0.25     +     0.125

=    11.375   

例题2:  1001101.01转化为十进制是多少?

解=1*2^0  +  0*2^1  +  1*2^2  +   1*2^3   +  0*2^4  +   0*2^5  +  1*2^6  +  0*2^(-1)  +  1*2^(-2)

   = 1   +   0  +   4   +   8    +   0   +  0   +   64   +   0   +  0.25

   =77.25

八进制转十进制

方法:按权展开

例题1:  将八进制数324.10转为十进制是多少?

解析:

以小数点为分界线.. 5   4    3   2    1    0  .  -1   -2    -3    -4...

小数点左边 从0开始往左依次增加   小数点右边从-1开始向右依次减小

          3    2    4    .    1    0  

          2    1    0         -1  -2 

解:4*8^0   +   2*8^1   +   3*8^2   +    1*8^(-1)   +  0*8^(-2)

=   4   +   16   +   192   +     0.125

=   212.125

例题2: 将八进制数1216.10转为十进制是多少?

解 :6*8^0  +  1*8^1   +   2*8^2   +   1*8^3   +    1* 8^(-1)  +  0*8^(-2)

=6   +   8    +   128  +   512    +   0.125   +   0

= 654.125

十六进制转十进制

方法:按权展开

例题1: 将十六进制数A10B.8转化为十进制

解析: 

在16进制里  A=10    B=11   C=12   D=13   E=14   F=15  

以小数点为分界线... 5   4    3   2    1    0  .  -1   -2    -3    -4..

小数点左边 从0开始往左依次增加   小数点右边从-1开始向右依次减小

        A      1    0    B   .    8 

        3      2    1    0       -1  

解: 11*16^0  +   0*16^1  +   1*16^2   +  10*16^3  +   8*16^(-1)

=  11  +   0   +   256   +   40960   +   0.5

 =41227.5

例题2:  BAEF.A转为十进制是多少?

解:15*16^0  +   14*16^1   +  10*16^2   +   11*16^3  +  10*16^(-1)

= 15   +   224   +   2560   +   45056  +   0.625

=47855.625

十进制转二进制

方法:    整数部分:除以二取余数,由下往上排,小数部分:乘二取整,由下往上排

例题1:  十进制数15.25转化为二进制是多少?    1111.01

整数:   15  ÷  2  =  7   余1

            7    ÷  2  =3    余1

            3    ÷  2  =1    余1

            1    ÷ 2  =0   余1   (一定要除到0为止)   

             从下往上排   1111

小数:   0.25   *  2   =   0.5    取0    (不足1的取0)

           0.5    *   2   =  1.0     取1     

(需要一直乘到没有小数或者出题人规定的位数才行)

          从上往下排   01

例题2 :十进制数95.75转为二进制是多少? 1011111.11

整数:   95    ÷   2   =47     余1

           47    ÷   2   =23     余1

           23    ÷   2   =11     余1

           11     ÷   2   =5      余1

            5     ÷    2   =2      余1

            2     ÷    2   =1      余0

            1    ÷     2  =0       余1 

            从下往上排    1011111

小数:    0.75   *   2    =    1.5      取1    (1.5 - 1=0.5)

             0.5    *    2   =    1.0       取1

            从上往下     11

十进制转八进制

方法:    整数部分:除以八取余数,由下往上排,小数部分:乘八取整,由下往上排

例题1:  十进制数15.25转化为八进制是多少?  17.2

整数:   15   ÷  8  =1   余7 

           1     ÷   8  =0   余1

            从下往上   17

小数:    0.25   *    8   =   2.0   取2

           从上往下   2

例题2:  十进制数95.75转化为八进制是多少?   137.6

整数:    95   ÷    8    =    11    余7

            11   ÷    8    =     1     余3

             1   ÷     8    =     0     余1

            从下往上   137

小数:     0.75    *     8     =   6.0     取6

            从上往下   6

十进制转十六进制

方法:    整数部分:除以十六取余数,由下往上排,小数部分:乘十六取整,由下往上排

例题1:  十进制数95.75转化为十六进制是多少?  5F.C

整数:   95    ÷    16   =    5     余15    15=F

           5    ÷     16  =    0        余5

            从下往上   5F

小数     0.75   *    16   =    12.0    取12    12=C

             从上往下   C

二进制转八进制

一位八进制数由三位二进制数来表示

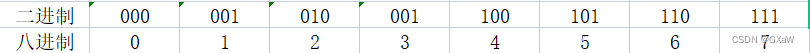
0  0   0

4   2  1

例题1:  二进制数11100111.0101101转化为八进制是多少?  347.264

解析:  以小数点为界  小数点往左每三位为一组,数到头不足三个的前面补0补足三位 

小数点往右每三位为一组,数到头不足三个的后面补0补足三位  

解:   011   100   111.    010   110   100 

          3        4      7   .     2       6       4

八进制转二进制

三位二进制组成一位八进制

0  0   0

4   2  1

例题1:  八进制数 347.264转化为二进制是多少? 11100111.0101101

解:    3        4      7   .     2       6       4

       011   100   111.    010   110    100 

补充:  整数二进制开头的0可以省略,结尾的0不可以省略

          小数二进制开头的0不可以省略,结尾的0可以省略

二进制转十六进制

一位十六进制数由四位二进制数来表示

 例题1:  二进制数11100111.0101101转化为十六进制是多少?E7.5A

解析:  以小数点为界  小数点往左每四位为一组,数到头不足四个的前面补0补足四位 

小数点往右每四位为一组,数到头不足四个的后面补0补足四位  

解:   1110     0111.    0101    1010

         E          7    .      5          A

十六进制转化为二进制

四位二进制组成一位十六进制

0    0   0   0

8    4    2   1

例题:十六进制数E7.5A转化为二进制数是多少?11100111.0101101

解   E       7        .5        A

   1110    0111   .0101    1010

十六进制转八进制

需经过中间商  二进制

例题  十六进制数E7.5A转化为八进制是多少?347.264

先转二进制:   

E          7 .          5           A

1110     0111.    0101    1010

二进制转八进制

011   100   111.    010   110   100 

 3        4      7   .     2       6       4

八进制转十六进制

需经过中间商  二进制

例题  八进制数347.264转化为十六进制是多少?E7.5A

先转二进制:   

3        4      7   .     2       6       4

011   100   111.    010   110    100

二进制转十六进制 

1110     0111.    0101    1010

 E          7    .      5          A

拓展:  进制方程

例题1:   某进制下152等于十六进制下的6A,求进制

  解:设该进制为R

       先将双方转化为二进制

列出式子    2*R^0  +  5*R^1 + 1*R^2 = 10*16^0 + 6*16^1

                          2 +5R + R^2 = 10 +96

                                            R = 8

例题2:   某进制下4+5=11 成立  求 5+6=?

解:设该进制为R

         4* R^0  +  5*R^0  =  1*R^0  + 1*R^1

                             R= 8

八进制逢八进一  4+5  = 4+4+1=11

所以 5+6=5+3+3=13

方法总结

1. R进制(二,八,十六)转十进制

按权展开,每个数乘R的多少次方

2.十进制转R进制

整数:除R取余  小数:乘R取整

3.二转八    三位合一     八转二    一位拆三    421

4.二转十六   四位合一    十六转二   一位拆四   8421

结束:

进制转换是计算机学科一个很基础的知识,但是用处很广泛,而转换的种类较多,容易犯糊涂,我把所有的转换方式都列了出来,就是为了少犯错误.

因为手机端与电脑端的排版差异,可能会比较乱

制作较为粗糙,如果有错,请各位大佬帮忙指正