字典学习（KSVD）详解

关于字典学习

对于一个事物，我们如何表征它呢？很明显，这个事物是有特征的，或者说，这个事物它是由许多个不同的特征经过一定的组合而形成的。字典学习的目标是提取实物的最本质特征。用字典来表征该事物的特征。（用尽可能少的资源表示尽可能多的知识，这种表示还能带来一个附加的好处，即计算速度快）
当提取出了事物的特征，这就相当于一种降维。
对于如何理解字典学习，我想到这样一个例子，比如一堆三维向量，找寻它们的特征，实际上，我们可以用三维直角坐标系（x，y，z三个单位向量）来表征它们，这三个向量通过组合可以表示所有的三维向量，它们就是我们的字典，再搭配上每个三维向量的x，y，z组合方式（稀疏编码），也就可以还原成那一堆三维向量了。

SVD

在理解KSVD之前，首先需要了解的是SVD（奇异值分解）。学习过矩阵理论的同学对SVD肯定是不陌生的。
在了解奇异值分解之前，需要了解一下特征值分解。所谓特征值分解，是为了提取出一个矩阵的特征。特征值，特征向量。这都是我们老生常谈的问题了。这里对于一个方阵$A$，我们又这样的定义：$Ax=\lambda x$,其中 $\lambda$ 是 $A$ 的特征值，$x$ 就是我们 $A$ 的对应 $\lambda$ 的特征向量。当矩阵可以相似对角化时，矩阵 $A$ 便可以被分解为：$$A=Q\Lambda Q^{-1}$$ 其中 $Q$ 是矩阵 $A$ 的特征向量组成的矩阵，$\Lambda$ 是一个对角阵，其对角线上的元素是 $A$ 的特征值。
一个矩阵其实就是一个线性变换，当我们将矩阵成以向量之后，其实就是对这个向量进行了线性变换。对应我们的特征值分解，分解的 $\Lambda$ 矩阵是一个对角阵，我们将其中的特征值从大到小排列，这些特征值对应的特征向量就是描述这个矩阵从主要到次要的变化方向。通过特征值分解得到前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。利用这前N个变化方向，我们就可以近似矩阵，也就是提取这个矩阵的特征。总的来说，特征向量表示特征，特征值表示特征的重要程度，可以把它在应用中当做权重。这种分解方法很好，但是也有特别明显的局限性，那就是它只适合方阵。
所以下面就要引出更适合一般矩阵的分解方式。也就是奇异值分解方法。我们在课上学过，这里我们设矩阵 $A$ 是 $m\ast n$ 的。奇异值分解形式为：$$A=U\Sigma V^T$$其中$U$是一个 $m\ast m$ 的酉矩阵，其里面的向量是相互正交的，我们称它们为做左奇异向量；$\Sigma$ 是一个 $m\ast n$ 的矩阵，只有对角线上的元素非零，这些值就是我们的奇异值，$V^T$ 是一个 $n\ast n$ 的矩阵，和一样，它也是酉矩阵，里面的向量也是互相正交的，称为右奇异向量。我们将矩阵 $A$ 的转置乘上它自己，便会得到一个方阵，用这个方阵来求特征值：$$A^{T}A{v}_i={\lambda }_i{v}_i$$ 这里的 $v_i$ 就是右奇异向量，$${\sigma }_i=\sqrt{{\lambda }_i}$$ $$u_i=\frac{A{v}_i}{{\sigma }_i}$$同理 $v_i$ 是我们的左奇异向量。我们这里的 $\sigma$ 就是奇异值。在矩阵中，我们让它以从小到大的顺序排列。在大多数情况下，我们会得到很好的结果，就是少部分的奇异值的和占了全部奇异值的和的大多数，那么我们就可以用前 $t$ 个奇异值来近似的描述矩阵。
对于一个矩阵，我们可以选取 $U$ 的前 $t$ 列，$\Sigma$ 的前 $t$ 个奇异值，$V_T$ 的前 $t$ 行，它们分别相乘累加的结果就可以近似表示我们的 $A$矩 阵，这不仅是一种近似，也相当于一种降维。

字典学习

字典学习主要是将原始样本 $Y$ 给分解中字典矩阵 $D$ 和稀疏码矩阵 $X$ ，这里的稀疏码 $X$ 自然是十分稀疏，数据量比较少。字典 $D$ 里便存储了原始样本 $Y$ 中的特征，而稀疏码则是用表示原始样本使用特征来组合成自己的方式。
理想情况是$$Y_{m\ast n}=D_{m\ast s}\ast X_{s\ast n}$$ 当 $s$ 远小于 $m$ 与 $n$ 时，$D$ 和 $X$ 的维度会远低于原来的 $Y$。当我们把矩阵 $X_{s\ast n}$ 的看做列向量形式 $(x_1,x_2...x_n)$，然后$$Y=D\ast (x_1,x_2...x_n)=D\ast x_1，D\ast x_2，...，D\ast x_n$$ 这里 $D\ast x_i$ 就是Y中的第 $i$ 列向量，我们可以用一个示意图来理解。

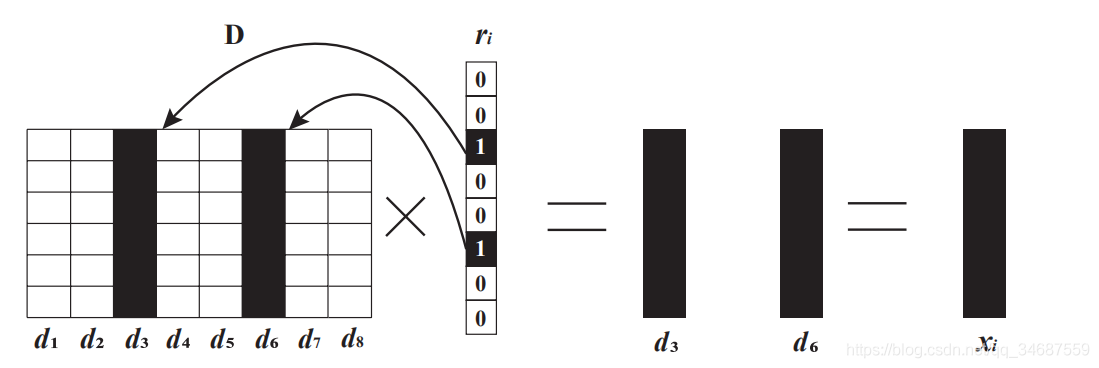
（图片来源Network Sparse Representation: Decomposition, Dimensionality-Reduction and Reconstruction）

求解过程

为了得到 $D$ 和 $X$，这里需要进行求解。这里提出一个优化问题：
$$mi{n}_{D,X}{\Vert Y-DX\Vert }_F^2,s.t.\forall i,{\Vert x_i\Vert }_0\le \epsilon$$
该优化问题就是在约束条件 $x_i$ 的零范数尽量小的情况下，原矩阵与分解的字典矩阵和稀疏码矩阵乘积的差值的矩阵二范数最小，此时的的字典矩阵$D$和稀疏码矩阵 $X$ 是多少。

说白了就是，稀疏码矩阵比较稀疏的情况下，追求 $Y$ 和 $DX$ 差值最小(可以以通过 $DX$ 来还原出$Y$)，求 $D$ 和 $X$ 。（这里可以把目标函数和约束函数调换位置求解，本质上没有什么区别，只是这一种更容易理解）
然后就是如何求解这个优化问题了，这里的求解思路是对字典矩阵的每一列和稀疏码矩阵的每一行来进行更新，多次迭代，从而最终实现 $D$ 与 $X$ 的求解。

这里假设是在迭代过程中的某一步，字典矩阵和稀疏矩阵都是有的，只是还不是最终结果。那么此时假设要更新的是字典的第i列和稀疏矩阵的第i行。优化目标公式是上面提到过的$$mi{n}_{D,X}{\Vert Y-DX\Vert }_F$$ 这里需要对该公式进行变形，首先将 $DX$ 写成列向量乘以行向量形式（为什么这样写呢，因为我们这里要更新的就是字典的第i列和稀疏矩阵的第i行）。从而，优化目标公式变成了$$mi{n}_{D,X}{\Vert Y-\sum _{j=1}^s{d}_j{x}_j\Vert }_F$$ 然后将要更新的 $d_i,x_i$ 抽取出来，公式变成了$$mi{n}_{D,X}{\Vert Y-\sum _{j=1,j\ne i}^s{d}_j{x}_j-d_i{x}_i\Vert }_F$$ 此时将前面两项合并，则就得到了这样一个式子$$mi{n}_{D,X}{\Vert E_i-d_i{x}_i\Vert }_F$$ 此时优化问题就变成了这个。来分析一下这个式子，首先 $E_i$ 是一个矩阵，$d_i,x_i$ 也是一个矩阵，它们是同维度的；然后 $E_i$是和$d_i,x_i$ 毫不相关的，因为它并没有计算有关 $i$ 的值。
这里我们可以这样理解：$DX$ 是字典矩阵乘以稀疏码矩阵，就是我们恢复的结果，那么 $Y-DX$ 就是原始矩阵与我们恢复矩阵的误差。而这个误差项再减去 $d_i,x_i$ 就是不考虑字典矩阵第$i$行和稀疏码矩阵第 $i$ 行的误差。当执行更新字典矩阵第 $i$ 行和稀疏码矩阵第 $i$ 行时，更新的标准是，用新的 $d_i,x_i$ 去弥补其他行列造成的误差。（有点贪心的感觉）

这里的 $E_i$ 是很好算的，直接 $$Y-\sum _{j=1,j\ne i}^s{d}_j{x}_j$$ 即可求得。不过这里还没这么简单，用于我们要进行多次迭代，有一个问题出现了，你如何保证稀疏码第 $i$ 行很稀疏呢（很多0呢），当你更新了字典矩阵第 $i$ 行和稀疏码矩阵第 $i$ 行，然后继续往后更新，进入下一次大的迭代，然后再来更新稀疏码矩阵第 $i$ 行，此时的 $E_i$ 都不一样了，此时，你完全无法控制第$i$行的稀疏情况，有可能会更稀疏，有可能会不变，有可能会更稠密，这是完全不可控的。
所以在这里，要进行一个操作，就是根据之前的$x_i$的情况，将$x_i$中非零元素提取出来形成新的行向量 $x_i^{\prime }$，然后将$x_i$非零元素与 $E_i$ 对应的列提取出来形成新的误差矩阵 ${E_i}^{\prime }$，显然，${E_i}^{\prime }$的维度和 $d_i{x}_i^{\prime }$ 的维度还是一致的。这里给出一个示意图：

（图片来源于https://www.cnblogs.com/endlesscoding/p/10090866.html，其中$E_k$就是本文中的$E_i$，）

（这里我写的不是很清楚，即使看了示意图可能也不是很理解，也有小伙伴问这里，为什么要将Xi中的非零元素提取出来形成行的Xi’，并构建新的Ei’呢？所以我在文章末尾进行了补充，该补充内容建议在阅读完全文之后对此处抱有疑惑再阅读，当然，如果理解了也可以不读）

然后我们的优化目标公式就变成了$$mi{n}_{D,X}{\Vert {E_i}^{\prime }-d_i{x_i}^{\prime }\Vert }_F^2$$ 对这个式子进行求解。
这个步骤的意义在于什么呢？在更新稀疏码第 $i$ 行时，选择继承之前该行稀疏码的稀疏性，本次更新我们只更新这个稀疏码的非零元素。这样就保证了一个什么问题呢，就是之前是零的元素在更新之后一定还是零，之前非零的元素呢，这就不好说，可能继续非零，也可能为零，这要取决于计算结果。
总之，这里提取非零元素与非零列，就保证了稀疏码只会朝着不变或者更稀疏的方向发展，而不会更稠密。然而，这也是有问题的，你只更新非零元素，虽然提取除了 ${E_i}^{\prime }$ ，但它和 $E_i$ ，是不一样的，无论你最后求得的 $d_i{x_i}^{\prime }$ 有多么解决 $E_i{;}^{\prime }$ ，它和 $E_i$ 的误差始终存在，无法解决。这就是保证了稀疏性，而损失了准确性，只能寄希望靠更多的迭代次数去弥补。

之后就是来求解$$mi{n}_{D,X}{\Vert {E_i}^{\prime }-d_i{x_i}^{\prime }\Vert }_F^2$$ 这是一个最小二乘问题，也就是你只能找 $d_i,{x_i}^{\prime }$ 去逼近 ${E_i}^{\prime }$ ，而无法直接求出其结果。这里就采用SVD（奇异值分解，前面讲的终于派上用场了）来求解。
求解的步骤就是将 ${E_i}^{\prime }$ 进行奇异值分解，得到$${E_i}^{\prime }=U\Sigma V^T$$ 然后取 $U$ 的第一列作为新的 $d_i$ ，而 $\Sigma V^T$ 乘积结果的第一行作为新的 ${x_i}^{\prime }$（其实就是 $\Sigma$ 的主对角线第一个元素乘以$V^T$的i第一行（这里 $\Sigma$ 中的奇异值按从大到小顺序来排列））。
至于为什么这样取呢？这在矩阵理论中是叫做秩一逼近。对于 ${E_i}^{\prime }=U\Sigma V^T$ ，我们可以将其表示如下$${E_i}^{\prime }=U\Sigma V^T={\sigma }_1{u}_1{v}_1^T+...+{\sigma }_k{u}_k{v}_k^T$$ 即分解成k个小矩阵，它们分别是 $U$ 的第 $i$ 行和 $\Sigma$ 的第 $i$ 个奇异值和 $V^T$ 的第 $i$ 个列向量的成绩，它们是同维度的矩阵。
同时因为奇异值分解的性质，$u_1,u_2...u_m$ 是相互正交的，同样，$v_1,v_2...v_n$ 是相互正交的，所以我们在计算 $E_i$ 的 $F$ 范数的平方时，便会有这样一个结果 $${\Vert {E_i}^{\prime }\Vert }_F^2={\sigma }_1^2\Vert u_1{v}_1^T\Vert +...{\sigma }_k^2\Vert u_k{v}_k^T\Vert ={\sigma }_1^2+...{\sigma }_k^2$$ 可以得到这样一个结果，因为 $\Sigma$ 中的奇异值是从大到小排列，而 ${\sigma }_1^2$ 占据了 ${\Vert {E_i}^{\prime }\Vert }_F^2$ 的大部分能量，所以用第一个小矩阵来近似原矩阵会让误差尽可能小，这样也能达到比较好的逼近效果。同时，这个小矩阵已经为我们分解好了 $u_k{v}_k^T$ ，所以我们选择这样的方式来进行求解。

至此，以上便是求解的全部过程。

不过还存在一个问题，就是我们假设更新时建立在字典和稀疏码已经存在情况下，那么第一次迭代时字典怎么办呢。我们可以采用对原始矩阵直接进行奇异值分解，取左歧义矩阵的前 $k$ 列作为字典，而稀疏码甚至可以选择全是1的矩阵，一开始误差较大，反正迭代次数够的话也是可以解决的。

补充

这里接着上面解释为什么要将Xi中的非零元素提取出来形成行的Xi’，并构建新的Ei’来进行求解的问题。
答曰：
这里是假设是某一次迭代更新字典的某一列和稀疏码某一行时，你现在的稀疏码假设是[0,0,1,0,1,1]，现在你要对残差Ei来进行奇异值分解，用最大能量来逼近对吧，但如果你直接对Ei进行分解，你怎么保证你的稀疏码更稀疏呢，无法保证，你可能会得到[1,2,3,1,1,1]这样的稀疏码，这种稀疏码比之前的还更离谱，一点都不稀疏，我们进行字典学习的目的有二，一是为了使分解的结果逼近原始样本，二是让稀疏码尽量稀疏，显然现在的更新无法满足我们的目的。所以我们采取这样方式，对于稀疏码[0,0,1,0,1,1]，为了保证之后更新的稀疏码往更稀疏的方向走，我们把其中非零元素提取出来[0,0,1,0,1,1]就提取出[1,1,1]，也就是第2,4,5列，对应的Ei也提取出2,4,5列形成Ei’，那么此时再奇异值分解，得到的新稀疏码假设是[a,b,c]，那么我们来更新稀疏码，就是[0,0,a,0,b,c]，（原来的0不动，只更新非零元素），那么无论a,b,c为何值，我们的这行稀疏码的稀疏程度都不会越更新越差，只会往稀疏性越好或不变的方向走。

参考资料

本文是我阅读了部分博客之后写的，其中KSVD的核心就在于它的对每行每列进行更新的方式上，求解其实并不是重点。
本文主要参考了
https://www.cnblogs.com/endlesscoding/p/10090866.html
https://blog.csdn.net/jzz3933/article/details/90599816