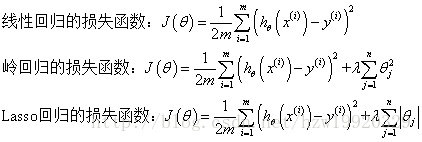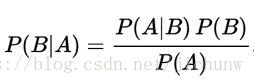菜鸟追梦旅行

这个屌丝很懒，什么也没留下！

热门标签

【面试】AI算法工程师---面试题！（第二部分：AI部分）_ai算法工程师面试题

作者：菜鸟追梦旅行 | 2024-03-26 01:33:54

踩

ai算法工程师面试题

【知识有点多，重点部分提到前面来(机器学习+cnn)】

一、机器学习（40%）

1.机器学习知识结构图（每个算法补充一下）

2.SGD,Momentum,Adagrad,Adam原理

模型的优化方法：

SGD、Momentum是针对梯度的，Adagard、Adam是针对学习率的。

（1）随机梯度下降SGD

随机梯度下降SGD，每一轮用随机的一个样本数据集mini-batch的梯度,然后对参数进行跟新。（求梯度，不是用所有数据集）

（2）Momentum

Momentum参考了动量的概念,前几次的梯度也会参与计算,但前几轮的梯度有一定的衰减。

（3）Adagrad

Adagard在训练的过程中可以自动变更学习的速率,设置一个全局的学习率,而实际的学习率与以往的参数模和的开方成反比。

（4）Adam

Adam利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率,在经过偏置的校正后,每一次迭代后的学习率都有个确定的范围,使得参数较为平稳。

3.L1不可导的时候该怎么办？

什么是L1？

是损失函数的正则化项，包括L1正则项和L2正则化项，均可防止过拟合。L1可能不可导。

L1正则化方法（岭回归，平方），L2正则化方法（Lasso回归，绝对值）

当L1不可导,梯度下降不再有效,可以使用坐标轴下降法。

梯度下降是沿着当前点的负梯度方向进行参数更新；

坐标轴下降是沿着坐标轴的方向,假设有m个特征个数,坐标轴下降法进参数更新的时候,先固定m-1个值,然后再求另外一个的局部最优解,从而避免损失函数不可导问题。

Proximal Aglorithm（近端算法）是在目标函数F不满足处处可微条件时，可以转而去优化目标函数的上界的自然结果。

4.sigmoid函数特性。

激活函数：

sigmoid特性：

函数在定义域内为连续和光滑的函数

处处可导,导数为

5.矩阵正定性的判断,Hessian矩阵正定性在梯度下降中的应用。

若矩阵所有特征值均不小于0,则判定为半正定。

若矩阵所有特征值均大于0,则判定为正定。

在判断优化算法的可行性时Hessian矩阵的正定性起到了很大的作用,若Hessian正定,则函数的二阶偏导恒大于0,函数的变化率处于递增状态。在牛顿法等梯度方法中,Hessian矩阵的正定性可以很容易的判断函数函数是否有凸性，也就是是否可收敛到局部或全局最优解。

6、PCA。

PCA是比较常见的线性降维方法,通过线性投影将高维数据映射到低维数据中,所期望的是在投影的维度上,新特征自身的方差尽量大,方差越大特征越有效,尽量使产生的新特征间的相关性更小。

PCA算法的具体操作：对所有的样本进行中心化操作,计算样本的协方差矩阵,然后对协方差矩阵做特征值分解,取最大的n个特征值对应的特征向量构造投影矩阵。

7、拟牛顿法的原理

牛顿法的收敛速度快,迭代次数少,但是Hessian矩阵很稠密时,每次迭代的计算量很大,随着数据规模增大,Hessian矩阵也会变大,需要更多的存储空间以及计算量。

拟牛顿法就是在牛顿法的基础上引入了Hessian矩阵的近似矩阵,避免了每次都计算Hessian矩阵的逆,在拟牛顿法中,用Hessian矩阵的逆矩阵来代替Hessian矩阵,虽然不能像牛顿法那样保证最优化的方向,但其逆矩阵始终是正定的,因此算法始终朝最优化的方向搜索。

8.交叉熵公式（用来算分类的loss）：

$H(p,q)=-\sum_{i=1}^{n} p(x_i)log(q(x_i))$ （p、q是y，y’转化来的）

9.LR公式的推导（LR代表逻辑回归）

逻辑回归本质上跟线性回归类似，只是在特征到结果的映射中加入了一层逻辑函数g(z)，即先把特征线性求和，然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0和1。g(z)为sigmoid函数：

则

逻辑回归用来分类0/1 问题，也就是预测结果属于0 或者1 的二值分类问题。这里假设了二值满足伯努利分布，也就是

对于训练数据集，特征数据x={x1, x2, … , xm}和对应的分类标签y={y1, y2, … , ym}，假设m个样本是相互独立的，那么，极大似然函数为：

log似然为：

如何使其最大呢？与线性回归类似，我们使用梯度上升的方法（求最小使用梯度下降），那么

如果只用一个训练样例（x，y），采用随机梯度上升规则，那么随机梯度上升更新规则为：

损失函数：

m为样本个数,为模型对样本i的预测结果,为样本i的真实标签。

10.回归问题，损失函数的三种形式：

（岭回归-L1正则项-平方，Lasso回归-L2正则项-绝对值）

11.Sfit特征提取和匹配的具体步骤（open-cv3那本书抽空看完）

生成高斯差分金字塔,

尺度空间构建,

空间极值点检测,

稳定关键点的精确定位,

稳定关键点方向信息分配,

关键点描述,

特征点匹配。

12.逻辑回归怎么实现多分类？

（1）softmax分类器（多分类）

修改逻辑回归的损失函数,使用softmax函数构造模型解决多分类问题。softmax分类模型会有相同于类别数的输出,输出的值为对于样本属于各个类别的概率,最后对于样本进行预测的类型为概率值最高的那个类别。

（2）相应类别个数的逻辑回归分类器。

根据每个类别都建立一个二分类器,本类别的样本标签定义为0,其它分类样本标签定义为1,则有多少个类别就构造多少个逻辑回归分类器。

若所有类别之间有明显的互斥则使用softmax分类器,若所有类别不互斥有交叉的情况则构造相应类别个数的逻辑回归分类器。

6.SVM中什么时候用线性核什么时候用高斯核?

当数据的特征提取的较好,所包含的信息量足够大,很多问题是线性可分的那么可以采用线性核。

若特征数较少,样本数适中,对于时间不敏感,遇到的问题是线性不可分的时候可以使用高斯核来达到更好的效果。

7.什么是支持向量机,SVM与LR的区别?

支持向量机：

为一个二分类模型,它的基本模型定义为特征空间上的间隔最大的线性分类器。而它的学习策略为最大化分类间隔,最终可转化为凸二次规划问题求解。

LR：

LR是参数模型,SVM为非参数模型。LR采用的损失函数为logisticalloss,而SVM采用的是hingeloss。在学习分类器的时候,SVM只考虑与分类最相关的少数支持向量点。LR的模型相对简单,在进行大规模线性分类时比较方便。

9.朴素贝叶斯（naive Bayes）法的要求是？

贝叶斯定理、特征条件独立假设

解析：朴素贝叶斯属于生成式模型，学习输入和输出的联合概率分布。给定输入x，利用贝叶斯概率定理求出最大的后验概率作为输出y。

10.训练集中类别不均衡，哪个参数最不准确？

准确度（Accuracy）

解析：举例，对于二分类问题来说，正负样例比相差较大为99:1，模型更容易被训练成预测较大占比的类别。因为模型只需要对每个样例按照0.99的概率预测正类，该模型就能达到99%的准确率。

11.SVM的作用，基本实现原理；

SVM可以用于解决二分类或者多分类问题，此处以二分类为例。SVM的目标是寻找一个最优化超平面在空间中分割两类数据，这个最优化超平面需要满足的条件是：离其最近的点到其的距离最大化，这些点被称为支持向量。

解析：建议练习推导SVM，从基本式的推导，到拉格朗日对偶问题。

12.SVM的硬间隔，软间隔表达式；

左边为硬间隔；右边为软间隔

解析：不同点在于有无引入松弛变量

13.SVM使用对偶计算的目的是什么，如何推出来的，手写推导；

（1）方便核函数的引入；

（2）原问题的求解复杂度与特征的维数相关，而转成对偶问题后只与问题的变量个数有关。由于SVM的变量个数为支持向量的个数，相较于特征位数较少，因此转对偶问题。通过拉格朗日算子发使带约束的优化目标转为不带约束的优化函数，使得W和b的偏导数等于零，带入原来的式子，再通过转成对偶问题。

14.SVM的物理意义是什么；

构造一个最优化的超平面在空间中分割数据

15.如果给你一些数据集，你会如何分类（我是分情况答的，从数据的大小，特征，是否有缺失，分情况分别答的）；

根据数据类型选择不同的模型，如Lr或者SVM，决策树。假如特征维数较多，可以选择SVM模型，如果样本数量较大可以选择LR模型，但是LR模型需要进行数据预处理；假如缺失值较多可以选择决策树。选定完模型后，相应的目标函数就确定了。还可以在考虑正负样例比比，通过上下集采样平衡正负样例比。

解析：需要了解多种分类模型的优缺点，以及如何构造分类模型的步骤

16.如果数据有问题，怎么处理；

1.上下采样平衡正负样例比；2.考虑缺失值；3.数据归一化

解析：发散问题需要自己展现自己的知识面

17.分层抽样的适用范围

分层抽样利用事先掌握的信息,充分考虑了保持样本结构和总体结构的一致性,当总体由差异明显的几部分组成的时候,适合用分层抽样。

18.LR和线性回归的区别：

线性回归用来做预测,LR用来做分类。线性回归是来拟合函数,LR是来预测函数。线性回归用最小二乘法来计算参数,LR用最大似然估计来计算参数。线性回归更容易受到异常值的影响,而LR对异常值有较好的稳定性。

19.生成模型和判别模型基本形式，有哪些？

生成式：朴素贝叶斯、HMM、Gaussians、马尔科夫随机场

判别式：LR，SVM，神经网络，CRF，Boosting

详情：支持向量机

20.核函数的种类和应用场景。

线性核、多项式核、高斯核。

特征维数高选择线性核

样本数量可观、特征少选择高斯核（非线性核）

样本数量非常多选择线性核（避免造成庞大的计算量）

详情：支持向量机

21.分类算法列一下有多少种？应用场景。

单一的分类方法主要包括：LR逻辑回归，SVM支持向量机，DT决策树、NB朴素贝叶斯、NN人工神经网络、K-近邻；集成学习算法：基于Bagging和Boosting算法思想，RF随机森林,GBDT，Adaboost,XGboost。

22.SVM核函数的选择

当样本的特征很多且维数很高时可考虑用SVM的线性核函数。当样本的数量较多,特征较少时,一般手动进行特征的组合再使用SVM的线性核函数。当样本维度不高且数量较少时,且不知道该用什么核函数时一般优先使用高斯核函数,因为高斯核函数为一种局部性较强的核函数,无论对于大样本还是小样本均有较好的性能且相对于多项式核函数有较少的参数。

23.SVM的损失函数

24.核函数的作用

核函数隐含着一个从低维空间到高维空间的映射,这个映射可以把低维空间中线性不可分的两类点变成线性可分的。

25.SVM为什么使用对偶函数求解

对偶将原始问题中的约束转为了对偶问题中的等式约束,而且更加方便了核函数的引入,同时也改变了问题的复杂度,在原始问题下,求解问题的复杂度只与样本的维度有关,在对偶问题下,只与样本的数量有关。

26.ID3,C4.5和CART三种决策树的区别

ID3决策树优先选择信息增益大的属性来对样本进行划分,但是这样的分裂节点方法有一个很大的缺点,当一个属性可取值数目较多时,可能在这个属性对应值下的样本只有一个或者很少个,此时它的信息增益将很高,ID3会认为这个属性很适合划分,但实际情况下叫多属性的取值会使模型的泛化能力较差,所以C4.5不采用信息增益作为划分依据,而是采用信息增益率作为划分依据。但是仍不能完全解决以上问题,而是有所改善,这个时候引入了CART树,它使用gini系数作为节点的分裂依据。

27.SVM和全部数据有关还是和局部数据有关?

SVM只和分类界限上的支持向量点有关,换而言之只和局部数据有关。

28.为什么高斯核能够拟合无穷维度？

因为将泰勒展开式代入高斯核,将会得到一个无穷维度的映射。

29. 完整推导svm一遍，还有强化学习说一说，dqn的各种trick了解多少，以及都怎么实现。

SVM推导：

支持向量机是一种二分类模型，他的基本想法就是基于训练集和样本空间中找到一个最好的划分超平面，将两类样本分割开来，首先你就要知道什么样的划分发才能称为“最”好划分

看上图，二维平面上有两类样本，一类是用‘+’表示，另一类用‘-’表示，那么中间那几条划分线每条都能将两类样本分割开来，但我们我们一眼就注意到中间那条加粗的划分超平面，似乎他是最好的，因为两类的样本点都离他挺远的，专业点说就是该划分超平面对训练样本局部扰动的‘容忍’性最好。好，这还只是个二维平面，我们可以通过可视化大概寻找这样一个超平面，但如果三维，四维，五维呢，我们必须用我们擅长的数学去描述它，推导它。

在样本空间中，划分超平面可用表示，记为（w,b）,样本点（xi,yi）到划分超平面的函数间隔为
，几何间隔为：

若，可知函数间隔和几何间隔相等，若超平面参数w，b成比例的改变（超平面没有变），则函数间隔也是成比例的改变，而几何间隔不变。

支持向量机的基本想法就是求解能够正确划分训练数据集并且几何间隔最大的分离超平面，表达为数学公式即为：

其实函数间隔的取值并不影响最优化问题的解，假设将w和b成倍的改变为aw，ab，那么函数间隔也会相应变成a，函数间隔的对上面最优化问题的不等式没有影响，也对目标函数没有影响，因此为简便，取，而且我们注意到最大化等价于最小化（为啥取平方呢，因为后面好求导），便可得到下面支持线性可分（线性不可分的情况后面会提到）的支持向量机的最优化问题

这是一个凸二次优化的问题，可以直接求解，但是为了简便呢，我们要应用拉格朗日对偶性，求解他的对偶问题

其实求解对偶问题相比于原问题有一下几点好处(1).对偶问题更容易求解，因为不用求w了 (2)我们可以自然引入核函数，这样可以推广到线性不可分分类问题上

建立拉格朗日函数，引进拉格朗日乘子，定义拉格朗日函数：

根据原始问题的对偶性，原始问题的对偶性是极大极小问题，即

首先我们来求最小，零L(w,b,a)分别对w和b求导为零可

得

将其代入对偶问题，可得

解出alpha之后，那么w，b也相应得到啦

接下来，我们看看很有意思的上式不等式约束的kkt条件（不懂请百度）带给我们的信息

咦，对于任意训练样本，总有或者，也就是说最终与模型有关的的样本点都位于最大间隔的边界上，我们称之为支持向量，其余的样本点与模型无关

在前面的讨论中，我们都是聊的线性可分的情况，那么大多数情况下都线性不可分怎么办，比如这样（如左）

山人自有妙计，我们可以将样本先映射到高维特征空间，然后就可以继续分割了（如右）

前面我们说到了对偶问题是

公式中涉及到计算，xi，xj是映射到特征空间之后的内积，由于特征维数可能会很高，甚至是无穷多维，直接计算很困难，所以我们引入了核函数：

这样我们就可以不用麻烦的计算内积了

dqn的各种trick：

第一个Trick。DQN引入卷积层。模型通过Atari游戏视频图像了解环境信息并学习策略。DQN需要理解接收图像，具有图像识别能力。卷积神经网络，利用可提取空间结构信息卷积层抽取特征。卷积层提取图像中重要目标特征传给后层做分类、回归。DQN用卷积层做强化学习训练，根据环境图像输出决策。

第二个Trick。Experience Replay。深度学习需要大量样本，传统Q-Learning online update方法(逐一对新样本学习)不适合DQN。增大样本，多个epoch训练，图像反复利用。Experience Replay，储存Agent Experience样本，每次训练随机抽取部分样本供网络学习。稳定完成学习任务，避免短视只学习最新接触样本，综合反复利用过往大量样本学习。创建储存Experience缓存buffer，储存一定量较新样本。容量满了，用新样本替换最旧样本，保证大部分样本相近概率被抽到。不替换旧样本，训练过程被抽到概率永远比新样本高很多。每次需要训练样本，直接从buffer随机抽取一定量给DQN训练，保持样本高利用率，让模型学习到较新样本。

第三个Trick。用第二个DQN网络辅助训练，target DQN，辅助计算目标Q值，提供学习目标公式里的maxaQ(st+1,a)。两个网络，一个制造学习目标，一个实际训练，让Q-Learning训练目标保持平稳。强化学习 Q-Learning学习目标每次变化，学习目标分部是模型本身输出，每次更新模型参数会导致学习目标变化，更新频繁幅度大，训练过程会非常不稳定、失控，DQN训练会陷入目标Q值与预测Q值反馈循环(陷入震荡发散，难收敛)。需要稳定target DQN辅助网络计算目标Q值。target DQN，低频率、缓慢学习，输出目标Q值波动较小，减小训练过程影响。

第四个Trick。Double DQN。传统DQN高估Action Q值，高估不均匀，导致次优Action被高估超过最优Action。targetDQN 负责生成目标Q值，先产生Q(st+1,a)，再通过maxa选择最大Q值。Double DQN，在主DQN上通过最大Q值选择Action，再获取Action在target DQN Q值。主网选择Action，targetDQN生成Action Q值。被选择Q值，不一定总是最大，避免被高估次优Action总是超过最优Action，导致发现不了真正最好Action。学习目标公式：Target=rt+1+γ·Qtarget(st+1,argmaxa(Qmain(st+1,a)))。

第五个Trick。Dueling DQN。Dueling DQN，Q值函数Q(st,at)拆分，一部分静态环境状态具有价值V(st)，Value；另一部分动态选择Action额外带来价值A(at)，Advantage。公式，Q(st,at)=V(st)+A(at)。网络分别计算环境Value和选择Action Advantage。Advantage，Action与其他Action比较，零均值。网络最后，不再直接输出Action数量Q值，输出一个Value，及Action数量 Advantage值。V值分别加到每个Advantage值上，得最后结果。让DQN学习目标更明确，如果当前期望价值主要由环境状态决定，Value值大，所有Advantage波动不大；如果期望价值主要由Action决定，Value值小，Advantage波动大。分解让学习目标更稳定、精确，DQN对环境状态估计能力更强。

30.SVM所有核函数的了解应用，SVM的损失函数。

SVM核函数：

1 核函数本质

核函数的本质可以概括为如下三点：

1）实际应用中，常常遇到线性不可分的情况。针对这种情况，常用做法是把样例特征映射到高维空间中，转化为线性可分问题。

2）将样例特征映射到高维空间，可能会遇到维度过高的问题。

3）针对可能的维灾难，可以利用核函数。核函数也是将特征从低维到高维的转换，但避免了直接进行高维空间中的复杂计算，可以在低维上进行计算，却能在实质上将分类效果表现在高维上。

当然，SVM也能处理线性可分问题，这时使用的就是线性核了。

常用的核函数包括如下几个：线性核函数，多项式核函数，RBF核函数(高斯核)，Sigmoid核函数

2 线性核

2.1 线性核

SVM肯定是可以处理线性问题的，这个就是斯坦福课程里讲SVM时候，最开始讲解的部分，以线性问题入手进行讲解。

线性核计算为k(x1,x2)=，其实就是在原始空间中的内积。

2.2 线性SVM和逻辑回归

当SVM使用线性核时，在处理分类问题时，和逻辑回归比较有哪些异同，如何选择？

1）线性核SVM和逻辑回归本质上没有区别

2）n=特征数，m=训练样本数目

如果n相对m比较大，使用逻辑回归或者线性SVM，例如n=10000，m=10-1000

如果n比较小，m数值适中，使用高斯核的SVM，例如n=1-1000,m=10-10000

如果n比较小，m很大，构建更多特征，然后使用逻辑回归或者线性SVM

3 非线性核

常用的非线性核包括多项式核，RBF核（高斯核），sigmoid核。

RBF核通常是首选，实践中往往能表现出良好的性能。计算方法如下：

其中，如果σ选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果σ选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

多项式核计算方法如下：

sigmoid核函数计算方法如下：

采用Sigmoid函数作为核函数时，支持向量机实现的就是一种多层感知器神经网络，应用SVM方法，隐含层节点数目(它确定神经网络的结构)、隐含层节点对输入节点的权值都是在设计(训练)的过程中自动确定的。而且支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值，也保证了它对于未知样本的良好泛化能力而不会出现过学习现象。

4 如何选择

1）可以利用专家先验知识余弦选定核函数，例如已经知道问题是线性可分的，就可以使用线性核，不必选用非线性核

2）利用交叉验证，试用不同的核函数，误差最小的即为效果最好的核函数

3）混合核函数方法，将不同的核函数结合起来

我觉得问题是线性可分和线性不可分其中之一，那在选择核函数的时候，如果不清楚问题属于哪一类，就两类核都尝试一下，所以可以主要尝试线性核以及RBF核。

1） Linear核：主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想了。

2）RBF核：主要用于线性不可分的情形。参数多，分类结果非常依赖于参数。有很多人是通过训练数据的交叉验证来寻找合适的参数，不过这个过程比较耗时。

至于到底该采用哪种核，要根据具体问题，有的数据是线性可分的，有的不可分，需要多尝试不同核不同参数。如果特征的提取的好，包含的信息量足够大，很多问题都是线性可分的。当然，如果有足够的时间去寻找RBF核参数，应该能达到更好的效果。

没有一种黄金规则可以确定哪种核函数将推导出最准确的SVM，在实践中，核函数的选择一般并不导致准确率的很大差别。SVM总是发现全局解，而不是局部解。

5 其他

SVM的复杂度主要由支持向量数刻画，而不是数据的维度，因此相比其他方法，SVM不太容易过拟合。

SVM的损失函数：

1、Hinge损失函数

首先我们来看什么是合页损失函数（hinge loss function）：

hinge loss function

下标”+”表示以下取正值的函数，我们用z表示中括号中的部分：

也就是说，数据点如果被正确分类，损失为0，如果没有被正确分类，损失为z。合页损失函数如下图所示：

2、SVM损失函数

SVM的损失函数就是合页损失函数加上正则化项：

31.LR和SVM 区别

1）LR是参数模型，SVM是非参数模型。2）从目标函数来看，区别在于逻辑回归采用的是logistical loss，SVM采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。3）SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。4）逻辑回归相对来说模型更简单，好理解，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些，SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。5）logic 能做的 svm能做，但可能在准确率上有问题，svm能做的logic有的做不了。

32.朴素贝叶斯基本原理和预测过程

朴素贝叶斯分类和预测算法的原理

决策树和朴素贝叶斯是最常用的两种分类算法，本篇文章介绍朴素贝叶斯算法。贝叶斯定理是以英国数学家贝叶斯命名，用来解决两个条件概率之间的关系问题。简单的说就是在已知P(A|B)时如何获得P(B|A)的概率。朴素贝叶斯（Naive Bayes）假设特征P(A)在特定结果P(B)下是独立的。

1.概率基础：

在开始介绍贝叶斯之前，先简单介绍下概率的基础知识。概率是某一结果出现的可能性。例如，抛一枚匀质硬币，正面向上的可能性多大？概率值是一个0-1之间的数字，用来衡量一个事件发生可能性的大小。概率值越接近1，事件发生的可能性越大，概率值越接近0，事件越不可能发生。我们日常生活中听到最多的是天气预报中的降水概率。概率的表示方法叫维恩图。下面我们通过维恩图来说明贝叶斯公式中常见的几个概率。

在维恩图中：

S：S是样本空间，是所有可能事件的总和。

P(A)：是样本空间S中A事件发生的概率，维恩图中绿色的部分。

P(B)：是样本空间S中B事件发生的概率，维恩图中蓝色的部分。

P(A∩B)：是样本空间S中A事件和B事件同时发生的概率，也就是A和B相交的区域。

P(A|B)：是条件概率，是B事件已经发生时A事件发生的概率。

对于条件概率，还有一种更清晰的表示方式叫概率树。下面的概率树表示了条件概率P(A|B)。与维恩图中的P(A∩B)相比，可以发现两者明显的区别。P(A∩B)是事件A和事件B同时发现的情况，因此是两者相交区域的概率。而事件概率P(A|B)是事件B发生时事件A发生的概率。这里有一个先决条件就是P(B)要首先发生。

因为条件概率P(A|B)是在事件B已经发生的情况下，事件A发生的概率，因此P(A|B)可以表示为事件A与B的交集与事件B的比率。

该公式还可以转换为以下形式，以便我们下面进行贝叶斯公式计算时使用。

2.贝叶斯公式：

该公式同样可以转化为以下形式：

到这一步，我们只需要证明P(A∩B)= P(B∩A)就可以证明在已知P(A|B)的情况下可以通过计算获得P(B|A)的概率。我们将概率树转化为下面的概率表，分别列出P(A|B),P(B|A),P(A),和P(B)的概率。

通过计算可以证明P(A|B)*P(B)和P(B|A)*P(A)最后求得的结果是概率表中的同一个区域的值，因此：

我们通过P(A∩B)= P(B∩A)证明了在已知P(A|B)，P(A),和P(B)三个概率的情况下可以计算出P(B|A)发生的概率。整个推导和计算过程可以说得通。但从统计学的角度来看，P(A|B)和P(B|A)两个条件概率之间存在怎样的关系呢？我们从贝叶斯推断里可以找到答案。

3.贝叶斯推断：

贝叶斯推断可以说明贝叶斯定理中两个条件概率之间的关系。换句话说就是我们为什么可以通过P(A|B)，P(A),和P(B)三个概率计算出P(B|A)发生的概率。

在贝叶斯推断中，每一种概率都有一个特定的名字：

P(B)是”先验概率”(Prior probability)。

P(A)是”先验概率”(Prior probability)，也作标准化常量(normalized constant)。

P(A|B)是已知B发生后A的条件概率，叫做似然函数(likelihood)。

P(B|A)是已知A发生后B的条件概率，是我们要求的值，叫做后验概率。

P(A|B)/P(A)是调整因子，也被称作标准似然度（standardised likelihood）。

贝叶斯推断中有几个关键的概念需要说明下：

第一个是先验概率，先验概率是指我们主观通过事件发生次数对概率的判断。

第二个是似然函数，似然函数是对某件事发生可能性的判断，与条件概率正好相反。通过事件已经发生的概率推算事件可能性的概率。

维基百科中对似然函数与概率的解释：

概率：是给定某一参数值，求某一结果的可能性。

例如，抛一枚匀质硬币，抛10次，6次正面向上的可能性多大？

似然函数：给定某一结果，求某一参数值的可能性。

例如，抛一枚硬币，抛10次，结果是6次正面向上，其是匀质的可能性多大？

第三个是调整因子：调整因子是似然函数与先验概率的比值，这个比值相当于一个权重，用来调整后验概率的值，使后验概率更接近真实概率。调整因子有三种情况，大于1，等于1和小于1。

调整因子P(A|B)/P(A)>1：说明事件可能发生的概率要大于事件已经发生次数的概率。

调整因子P(A|B)/P(A)=1：说明事件可能发生的概率与事件已经发生次数的概率相等。

调整因子P(A|B)/P(A)<1：说明事件可能发生的概率与事件小于已经发生次数的概率。

因此，贝叶斯推断可以理解为通过先验概率和调整因子来获得后验概率。其中调整因子是根据事件已经发生的概率推断事件可能发生的概率（通过硬币正面出现的次数来推断硬币均匀的可能性），并与已经发生的先验概率（硬币正面出现的概率）的比值。通过这个比值调整先验概率来获得后验概率。

后验概率＝先验概率ｘ调整因子

33.请你说一说交叉熵，也可以再说一下其他的你了解的熵

为了更好的理解，需要了解的概率必备知识有：

大写字母X表示随机变量，小写字母x表示随机变量X的某个具体的取值；

P(X)表示随机变量X的概率分布，P(X,Y)表示随机变量X、Y的联合概率分布，P(Y|X)表示已知随机变量X的情况下随机变量Y的条件概率分布；

p(X=x)表示随机变量X取某个具体值的概率，简记为p(x)；

p(X=x,Y=y) 表示联合概率，简记为p(x,y)，p(Y=y|X=x)表示条件概率，简记为p(y|x)，且有：p(x,y)=p(x)*p(y|x)。

熵：如果一个随机变量X的可能取值为X={x1,x2,…,xk}，其概率分布为P(X=xi)=pi（i= 1,2,...,n），则随机变量X的熵定义为：

把最前面的负号放到最后，便成了：

上面两个熵的公式，无论用哪个都行，而且两者等价，一个意思（这两个公式在下文中都会用到）。

联合熵：两个随机变量X，Y的联合分布，可以形成联合熵Joint Entropy，用H(X,Y)表示。

条件熵：在随机变量X发生的前提下，随机变量Y发生所新带来的熵定义为Y的条件熵，用H(Y|X)表示，用来衡量在已知随机变量X的条件下随机变量Y的不确定性。

且有此式子成立：H(Y|X)=H(X,Y)-H(X)，整个式子表示(X,Y)发生所包含的熵减去X单独发生包含的熵。至于怎么得来的请看推导：

简单解释下上面的推导过程。整个式子共6行，其中

第二行推到第三行的依据是边缘分布p(x)等于联合分布p(x,y)的和；

第三行推到第四行的依据是把公因子logp(x)乘进去，然后把x,y写在一起；

第四行推到第五行的依据是：因为两个sigma都有p(x,y)，故提取公因子p(x,y)放到外边，然后把里边的-logp(x,y)-logp(x)）写成-log(p(x,y)/p(x)) ；

第五行推到第六行的依据是：p(x,y)=p(x)*p(y|x)，故p(x,y)/p(x)=p(y|x)。

相对熵：又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布，则p对q的相对熵是：

在一定程度上，相对熵可以度量两个随机变量的“距离”，且有D(p||q) ≠D(q||p)。另外，值得一提的是，D(p||q)是必然大于等于0的。

互信息：两个随机变量X，Y的互信息定义为X，Y的联合分布和各自独立分布乘积的相对熵，用I(X,Y)表示：

且有I(X,Y)=D(P(X,Y)||P(X)P(Y))。下面，咱们来计算下H(Y)-I(X,Y)的结果，如下：

通过上面的计算过程，我们发现竟然有H(Y)-I(X,Y)=H(Y|X)。故通过条件熵的定义，有：H(Y|X)=H(X,Y)-H(X)，而根据互信息定义展开得到H(Y|X)=H(Y)-I(X,Y)，把前者跟后者结合起来，便有I(X,Y)= H(X)+H(Y)-H(X,Y)，此结论被多数文献作为互信息的定义。

34.L1和L2正则化的区别

L1是模型各个参数的绝对值之和,L2为各个参数平方和的开方值。L1更趋向于产生少量的特征,其它特征为0,最优的参数值很大概率出现在坐标轴上,从而导致产生稀疏的权重矩阵,而L2会选择更多的矩阵,但是这些矩阵趋向于0。

35.Loss Function有哪些，怎么用？

平方损失（预测问题）、交叉熵（分类问题）、hinge损失（SVM支持向量机）、CART回归树的残差损失

36.线性回归的表达式，损失函数；

线性回归y=wx+b，w和x可能是多维。线性回归的损失函数为平方损失函数。

解析：一般会要求反向求导推导

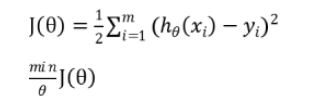
37.什么是DBSCAN？

DBSCAN是一种基于密度的空间聚类算法,它不需要定义簇的个数,而是将具有足够高密度的区域划分为簇,并在有噪声的数据中发现任意形状的簇,在此算法中将簇定义为密度相连的点的最大集合。

38.k-means算法流程

从数据集中随机选择k个聚类样本作为初始的聚类中心,然后计算数据集中每个样本到这k个聚类中心的距离,并将此样本分到距离最小的聚类中心所对应的类中。将所有样本归类后,对于每个类别重新计算每个类别的聚类中心即每个类中所有样本的质心,重复以上操作直到聚类中心不变为止。

39. LDA的原理

LDA是一种基于有监督学习的降维方式,将数据集在低维度的空间进行投影,要使得投影后的同类别的数据点间的距离尽可能的靠近,而不同类别间的数据点的距离尽可能的远。

40.介绍几种机器学习的算法，我就结合我的项目经理介绍了些RF, Kmeans等算法。

常见的机器学习算法：

1）. 回归算法：回归算法是试图采用对误差的衡量来探索变量之间的关系的一类算法。回归算法是统计机器学习的利器。常见的回归算法包括：最小二乘法（Ordinary Least Square），逻辑回归（Logistic Regression），逐步式回归（Stepwise Regression），多元自适应回归样条（Multivariate Adaptive Regression Splines）以及本地散点平滑估计（Locally Estimated Scatterplot Smoothing）。

2）. 基于实例的算法：基于实例的算法常常用来对决策问题建立模型，这样的模型常常先选取一批样本数据，然后根据某些近似性把新数据与样本数据进行比较。通过这种方式来寻找最佳的匹配。因此，基于实例的算法常常也被称为“赢家通吃”学习或者“基于记忆的学习”。常见的算法包括 k-Nearest Neighbor(KNN), 学习矢量量化（Learning Vector Quantization， LVQ），以及自组织映射算法（Self-Organizing Map，SOM）。深度学习的概念源于人工神经网络的研究。含多隐层的多层感知器就是一种深度学习结构。深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据的分布式特征表示。

3）. 决策树学习：决策树算法根据数据的属性采用树状结构建立决策模型，决策树模型常常用来解决分类和回归问题。常见的算法包括：分类及回归树（Classification And Regression Tree，CART），ID3 (Iterative Dichotomiser 3)，C4.5，Chi-squared Automatic Interaction Detection(CHAID), Decision Stump, 随机森林（Random Forest），多元自适应回归样条（MARS）以及梯度推进机（Gradient Boosting Machine，GBM）。

4）. 贝叶斯方法：贝叶斯方法算法是基于贝叶斯定理的一类算法，主要用来解决分类和回归问题。常见算法包括：朴素贝叶斯算法，平均单依赖估计（Averaged One-Dependence Estimators，AODE），以及Bayesian Belief Network（BBN）。

5）. 基于核的算法：基于核的算法中最著名的莫过于支持向量机（SVM）了。基于核的算法把输入数据映射到一个高阶的向量空间，在这些高阶向量空间里，有些分类或者回归问题能够更容易的解决。常见的基于核的算法包括：支持向量机（Support Vector Machine，SVM），径向基函数（Radial Basis Function，RBF)，以及线性判别分析（Linear Discriminate Analysis，LDA)等。

6）. 聚类算法：聚类，就像回归一样，有时候人们描述的是一类问题，有时候描述的是一类算法。聚类算法通常按照中心点或者分层的方式对输入数据进行归并。所以的聚类算法都试图找到数据的内在结构，以便按照最大的共同点将数据进行归类。常见的聚类算法包括 k-Means算法以及期望最大化算法（Expectation Maximization，EM）。

7）. 降低维度算法：像聚类算法一样，降低维度算法试图分析数据的内在结构，不过降低维度算法是以非监督学习的方式试图利用较少的信息来归纳或者解释数据。这类算法可以用于高维数据的可视化或者用来简化数据以便监督式学习使用。常见的算法包括：主成份分析（Principle Component Analysis，PCA），偏最小二乘回归（Partial Least Square Regression，PLS），Sammon映射，多维尺度（Multi-Dimensional Scaling, MDS）, 投影追踪（Projection Pursuit）等。

8）. 关联规则学习：关联规则学习通过寻找最能够解释数据变量之间关系的规则，来找出大量多元数据集中有用的关联规则。常见算法包括 Apriori算法和Eclat算法等。

9）. 集成算法：集成算法用一些相对较弱的学习模型独立地就同样的样本进行训练，然后把结果整合起来进行整体预测。集成算法的主要难点在于究竟集成哪些独立的较弱的学习模型以及如何把学习结果整合起来。这是一类非常强大的算法，同时也非常流行。常见的算法包括：Boosting，Bootstrapped Aggregation（Bagging），AdaBoost，堆叠泛化（Stacked Generalization，Blending），梯度推进机（Gradient Boosting Machine, GBM），随机森林（Random Forest）。

10）. 人工神经网络：人工神经网络算法模拟生物神经网络，是一类模式匹配算法。通常用于解决分类和回归问题。人工神经网络是机器学习的一个庞大的分支，有几百种不同的算法。（其中深度学习就是其中的一类算法，我们会单独讨论），重要的人工神经网络算法包括：感知器神经网络（Perceptron Neural Network）, 反向传递（Back Propagation），Hopfield网络，自组织映射（Self-Organizing Map, SOM）。学习矢量量化（Learning Vector Quantization， LVQ）。

RF：通过对训练数据样本以及属性进行有放回的抽样（针对某一个属性随机选择样本）这里有两种，一种是每次都是有放回的采样，有些样本是重复的，组成和原始数据集样本个数一样的数据集；另外一种是不放回的抽样，抽取出大约60%的训练信息。由此生成一颗CART树，剩下的样本信息作为袋外数据，用来当作验证集计算袋外误差测试模型；把抽取出的样本信息再放回到原数据集中，再重新抽取一组训练信息，再以此训练数据集生成一颗CART树。这样依次生成多颗CART树，多颗树组成森林，并且他们的生成都是通过随机采样的训练数据生成，因此叫随机森林。RF可以用于数据的回归，也可以用于数据的分类。回归时是由多颗树的预测结果求均值；分类是由多棵树的预测结果进行投票。正式由于它的随机性，RF有极强的防止过拟合的特性。由于他是由CART组成，因此它的训练数据不需要进行归一化，因为每课的建立过程都是通过选择一个能最好的对数据样本进行选择的属性来建立分叉，因此有以上好处的同时也带来了一个缺点，那就是忽略了属性与属性之间的关系。

K-meas：基本K-Means算法的思想很简单，事先确定常数K，常数K意味着最终的聚类类别数，首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，接着，重新计算每个类的质心(即为类中心)，重复这样的过程，知道质心不再改变，最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

初始化常数K，随机选取初始点为质心

重复计算一下过程，直到质心不再改变

计算样本与每个质心之间的相似度，将样本归类到最相似的类中

重新计算质心

输出最终的质心以及每个类.

41.KMeans讲讲，KMeans有什么缺点，K怎么确定

在k-means算法中，用质心来表示cluster；且容易证明k-means算法收敛等同于所有质心不再发生变化。基本的k-means算法流程如下：

选取k个初始质心（作为初始cluster）；

repeat：对每个样本点，计算得到距其最近的质心，将其类别标为该质心所对应的cluster；重新计算k个cluser对应的质心；

until 质心不再发生变化

k-means存在缺点：

1）k-means是局部最优的，容易受到初始质心的影响；比如在下图中，因选择初始质心不恰当而造成次优的聚类结果。

2）同时，k值的选取也会直接影响聚类结果，最优聚类的k值应与样本数据本身的结构信息相吻合，而这种结构信息是很难去掌握，因此选取最优k值是非常困难的。

K值得确定：

法1：(轮廓系数)在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分聚类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。

法2：(Calinski-Harabasz准则)

其中SSB是类间方差，，m为所有点的中心点,mi为某类的中心点；

SSW是类内方差，；

(N-k)/(k-1)是复杂度；

比率越大，数据分离度越大。

42.DBSCAN原理和算法伪代码，与kmeans，OPTICS区别

DBSCAN聚类算法原理

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法，它是一种基于高密度连通区域的、基于密度的聚类算法，能够将具有足够高密度的区域划分为簇，并在具有噪声的数据中发现任意形状的簇。我们总结一下DBSCAN聚类算法原理的基本要点：

DBSCAN算法需要选择一种距离度量，对于待聚类的数据集中，任意两个点之间的距离，反映了点之间的密度，说明了点与点是否能够聚到同一类中。由于DBSCAN算法对高维数据定义密度很困难，所以对于二维空间中的点，可以使用欧几里德距离来进行度量。

DBSCAN算法需要用户输入2个参数：一个参数是半径（Eps），表示以给定点P为中心的圆形邻域的范围；另一个参数是以点P为中心的邻域内最少点的数量（MinPts）。如果满足：以点P为中心、半径为Eps的邻域内的点的个数不少于MinPts，则称点P为核心点。

DBSCAN聚类使用到一个k-距离的概念，k-距离是指：给定数据集P={p(i); i=0,1,…n}，对于任意点P(i)，计算点P(i)到集合D的子集S={p(1), p(2), …, p(i-1), p(i+1), …, p(n)}中所有点之间的距离，距离按照从小到大的顺序排序，假设排序后的距离集合为D={d(1), d(2), …, d(k-1), d(k), d(k+1), …,d(n)}，则d(k)就被称为k-距离。也就是说，k-距离是点p(i)到所有点（除了p(i)点）之间距离第k近的距离。对待聚类集合中每个点p(i)都计算k-距离，最后得到所有点的k-距离集合E={e(1), e(2), …, e(n)}。

根据经验计算半径Eps：根据得到的所有点的k-距离集合E，对集合E进行升序排序后得到k-距离集合E’，需要拟合一条排序后的E’集合中k-距离的变化曲线图，然后绘出曲线，通过观察，将急剧发生变化的位置所对应的k-距离的值，确定为半径Eps的值。

根据经验计算最少点的数量MinPts：确定MinPts的大小，实际上也是确定k-距离中k的值，DBSCAN算法取k=4，则MinPts=4。

另外，如果觉得经验值聚类的结果不满意，可以适当调整Eps和MinPts的值，经过多次迭代计算对比，选择最合适的参数值。可以看出，如果MinPts不变，Eps取得值过大，会导致大多数点都聚到同一个簇中，Eps过小，会导致已一个簇的分裂；如果Eps不变，MinPts的值取得过大，会导致同一个簇中点被标记为噪声点，MinPts过小，会导致发现大量的核心点。

我们需要知道的是，DBSCAN算法，需要输入2个参数，这两个参数的计算都来自经验知识。半径Eps的计算依赖于计算k-距离，DBSCAN取k=4，也就是设置MinPts=4，然后需要根据k-距离曲线，根据经验观察找到合适的半径Eps的值，下面的算法实现过程中，我们会详细说明。对于算法的实现，首先我们概要地描述一下实现的过程：

1）解析样本数据文件。2）计算每个点与其他所有点之间的欧几里德距离。3）计算每个点的k-距离值，并对所有点的k-距离集合进行升序排序，输出的排序后的k-距离值。4）将所有点的k-距离值，在Excel中用散点图显示k-距离变化趋势。5）根据散点图确定半径Eps的值。）根据给定MinPts=4，以及半径Eps的值，计算所有核心点，并建立核心点与到核心点距离小于半径Eps的点的映射。7）根据得到的核心点集合，以及半径Eps的值，计算能够连通的核心点，得到噪声点。8）将能够连通的每一组核心点，以及到核心点距离小于半径Eps的点，都放到一起，形成一个簇。9）选择不同的半径Eps，使用DBSCAN算法聚类得到的一组簇及其噪声点，使用散点图对比聚类效果。

算法伪代码：

算法描述：

算法：DBSCAN

输入：E——半径

MinPts——给定点在E邻域内成为核心对象的最小邻域点数。

D——集合。

输出：目标类簇集合

方法：Repeat

1）判断输入点是否为核心对象

2）找出核心对象的E邻域中的所有直接密度可达点。

Until 所有输入点都判断完毕

Repeat

针对所有核心对象的E邻域内所有直接密度可达点找到最大密度相连对象集合，中间涉及到一些密度可达对象的合并。Until 所有核心对象的E领域都遍历完毕

DBSCAN和Kmeans的区别：

1)K均值和DBSCAN都是将每个对象指派到单个簇的划分聚类算法，但是K均值一般聚类所有对象，而DBSCAN丢弃被它识别为噪声的对象。

2)K均值使用簇的基于原型的概念，而DBSCAN使用基于密度的概念。

3)K均值很难处理非球形的簇和不同大小的簇。DBSCAN可以处理不同大小或形状的簇，并且不太受噪声和离群点的影响。当簇具有很不相同的密度时，两种算法的性能都很差。

4)K均值只能用于具有明确定义的质心（比如均值或中位数）的数据。DBSCAN要求密度定义（基于传统的欧几里得密度概念）对于数据是有意义的。

5)K均值可以用于稀疏的高维数据，如文档数据。DBSCAN通常在这类数据上的性能很差，因为对于高维数据，传统的欧几里得密度定义不能很好处理它们。

6)K均值和DBSCAN的最初版本都是针对欧几里得数据设计的，但是它们都被扩展，以便处理其他类型的数据。

7)基本K均值算法等价于一种统计聚类方法（混合模型），假定所有的簇都来自球形高斯分布，具有不同的均值，但具有相同的协方差矩阵。DBSCAN不对数据的分布做任何假定。

8)K均值DBSCAN和都寻找使用所有属性的簇，即它们都不寻找可能只涉及某个属性子集的簇。

9)K均值可以发现不是明显分离的簇，即便簇有重叠也可以发现，但是DBSCAN会合并有重叠的簇。

10)K均值算法的时间复杂度是O(m)，而DBSCAN的时间复杂度是O(m^2)，除非用于诸如低维欧几里得数据这样的特殊情况。

11)DBSCAN多次运行产生相同的结果，而K均值通常使用随机初始化质心，不会产生相同的结果。

12)DBSCAN自动地确定簇个数，对于K均值，簇个数需要作为参数指定。然而，DBSCAN必须指定另外两个参数：Eps（邻域半径）和MinPts（最少点数）。

13)K均值聚类可以看作优化问题，即最小化每个点到最近质心的误差平方和，并且可以看作一种统计聚类（混合模型）的特例。DBSCAN不基于任何形式化模型。

DBSCAN与OPTICS的区别：

DBSCAN算法，有两个初始参数E（邻域半径）和minPts(E邻域最小点数)需要用户手动设置输入，并且聚类的类簇结果对这两个参数的取值非常敏感，不同的取值将产生不同的聚类结果，其实这也是大多数其他需要初始化参数聚类算法的弊端。

为了克服DBSCAN算法这一缺点，提出了OPTICS算法（Ordering Points to identify the clustering structure）。OPTICS并不显示的产生结果类簇，而是为聚类分析生成一个增广的簇排序（比如，以可达距离为纵轴，样本点输出次序为横轴的坐标图），这个排序代表了各样本点基于密度的聚类结构。它包含的信息等价于从一个广泛的参数设置所获得的基于密度的聚类，换句话说，从这个排序中可以得到基于任何参数E和minPts的DBSCAN算法的聚类结果。

OPTICS两个概念：

核心距离：对象p的核心距离是指是p成为核心对象的最小E’。如果p不是核心对象，那么p的核心距离没有任何意义。

可达距离：对象q到对象p的可达距离是指p的核心距离和p与q之间欧几里得距离之间的较大值。如果p不是核心对象，p和q之间的可达距离没有意义。

算法描述：OPTICS算法额外存储了每个对象的核心距离和可达距离。基于OPTICS产生的排序信息来提取类簇。

43.请你说一说推荐系统常用的算法：FM，LR，Embedding

推荐算法：

基于人口学的推荐、基于内容的推荐、基于用户的协同过滤推荐、基于项目的协同过滤推荐、基于模型的协同过滤推荐、基于关联规则的推荐

FM：

LR：

逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层逻辑函数g(z)，即先把特征线性求和，然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0 和1。g(z)为sigmoid function.

则

sigmoid function 的导数如下：

逻辑回归用来分类0/1 问题，也就是预测结果属于0 或者1 的二值分类问题。这里假设了二值满足伯努利分布，也就是

其也可以写成如下的形式：

对于训练数据集，特征数据x={x1, x2, … , xm}和对应的分类标签y={y1, y2, … , ym}，假设m个样本是相互独立的，那么，极大似然函数为：

log似然为：

如何使其最大呢？与线性回归类似，我们使用梯度上升的方法（求最小使用梯度下降），那么。

如果只用一个训练样例（x，y），采用随机梯度上升规则，那么随机梯度上升更新规则为：

Embedding：

Embedding在数学上表示一个maping：，也就是一个function。其中该函数满足两个性质：1）injective （单射的）：就是我们所说的单射函数，每个Y只有唯一的X对应;2）structure-preserving（结构保存）：比如在X所属的空间上，那么映射后在Y所属空间上同理。

那么对于word embedding,就是找到一个映射(函数)将单词(word)映射到另外一个空间(其中这个映射具有injective和structure-preserving的特点),生成在一个新的空间上的表达，该表达就是word representation。

44.协同过滤的itemCF，userCF区别适用场景

Item CF 和 User CF两个方法都能很好的给出推荐，并可以达到不错的效果。但是他们之间还是有不同之处的，而且适用性也有区别。下面进行一下对比

计算复杂度：

Item CF 和 User CF 是基于协同过滤推荐的两个最基本的算法，User CF 是很早以前就提出来了，Item CF 是从 Amazon 的论文和专利发表之后（2001 年左右）开始流行，大家都觉得 Item CF 从性能和复杂度上比 User CF 更优，其中的一个主要原因就是对于一个在线网站，用户的数量往往大大超过物品的数量，同时物品的数据相对稳定，因此计算物品的相似度不但计算量较小，同时也不必频繁更新。但我们往往忽略了这种情况只适应于提供商品的电子商务网站，对于新闻，博客或者微内容的推荐系统，情况往往是相反的，物品的数量是海量的，同时也是更新频繁的，所以单从复杂度的角度，这两个算法在不同的系统中各有优势，推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。

适用场景：

在非社交网络的网站中，内容内在的联系是很重要的推荐原则，它比基于相似用户的推荐原则更加有效。比如在购书网站上，当你看一本书的时候，推荐引擎会给你推荐相关的书籍，这个推荐的重要性远远超过了网站首页对该用户的综合推荐。可以看到，在这种情况下，Item CF 的推荐成为了引导用户浏览的重要手段。同时 Item CF 便于为推荐做出解释，在一个非社交网络的网站中，给某个用户推荐一本书，同时给出的解释是某某和你有相似兴趣的人也看了这本书，这很难让用户信服，因为用户可能根本不认识那个人；但如果解释说是因为这本书和你以前看的某本书相似，用户可能就觉得合理而采纳了此推荐。

相反的，在现今很流行的社交网络站点中，User CF 是一个更不错的选择，User CF 加上社会网络信息，可以增加用户对推荐解释的信服程度。

45.推荐系统的大概步骤，解决冷启动

步骤：1）收集用户的所有信息。2）使用大数据计算平台对收集的信息进行处理，的到用户偏好数据。3）将偏好数据导入喜好类型计算算法中进行预算计算，的到预算结果。4）将推荐的结果导入数据库（redis、hbase）。5）发开一个推荐引擎，对外开放接口，输出推荐结果。

解决冷启动的方案：

1）提供非个性化的推荐

最简单的例子就是提供热门排行榜，可以给用户推荐热门排行榜，等到用户数据收集到一定的时候，再切换为个性化推荐。例如Netflix的研究也表明新用户在冷启动阶段确实是更倾向于热门排行榜的，老用户会更加需要长尾推荐

2）利用用户注册信息

用户的注册信息主要分为3种：（1）获取用户的注册信息；（2）根据用户的注册信息对用户分类；（3）给用户推荐他所属分类中用户喜欢的物品。

3）选择合适的物品启动用户的兴趣

用户在登录时对一些物品进行反馈，收集用户对这些物品的兴趣信息，然后给用户推荐那些和这些物品相似的物品。一般来说，能够用来启动用户兴趣的物品需要具有以下特点：

比较热门，如果要让用户对物品进行反馈，前提是用户得知道这是什么东西；

具有代表性和区分性，启动用户兴趣的物品不能是大众化或老少咸宜的，因为这样的物品对用户的兴趣没有区分性；

启动物品集合需要有多样性，在冷启动时，我们不知道用户的兴趣，而用户兴趣的可能性非常多，为了匹配多样的兴趣，我们需要提供具有很高覆盖率的启动物品集合，这些物品能覆盖几乎所有主流的用户兴趣

4）利用物品的内容信息

用来解决物品的冷启动问题，即如何将新加入的物品推荐给对它感兴趣的用户。物品冷启动问题在新闻网站等时效性很强的网站中非常重要，因为这些网站时时刻刻都有新物品加入，而且每个物品必须能够再第一时间展现给用户，否则经过一段时间后，物品的价值就大大降低了。

5）采用专家标注

很多系统在建立的时候，既没有用户的行为数据，也没有充足的物品内容信息来计算物品相似度。这种情况下，很多系统都利用专家进行标注。

6）利用用户在其他地方已经沉淀的数据进行冷启动

以QQ音乐举例：QQ音乐的猜你喜欢电台想要去猜测第一次使用QQ音乐的用户的口味偏好，一大优势是可以利用其它腾讯平台的数据，比如在QQ空间关注了谁，在腾讯微博关注了谁，更进一步，比如在腾讯视频刚刚看了一部动漫，那么如果QQ音乐推荐了这部动漫里的歌曲，用户会觉得很人性化。这就是利用用户在其它平台已有的数据。

再比如今日头条：它是在用户通过新浪微博等社交网站登录之后，获取用户的关注列表，并且爬取用户最近参与互动的feed（转发/评论等），对其进行语义分析，从而获取用户的偏好。

所以这种方法的前提是，引导用户通过社交网络账号登录，这样一方面可以降低注册成本提高转化率；另一方面可以获取用户的社交网络信息，解决冷启动问题。

7）利用用户的手机等兴趣偏好进行冷启动

Android手机开放的比较高，所以在安装自己的app时，就可以顺路了解下手机上还安装了什么其他的app。比如一个用户安装了美丽说、蘑菇街、辣妈帮、大姨妈等应用，就可以判定这是女性了，更进一步还可以判定是备孕还是少女。目前读取用户安装的应用这部分功能除了app应用商店之外，一些新闻类、视频类的应用也在做，对于解决冷启动问题有很好的帮助。

46.用mapreduce实现10亿级以上数据的kmeans。

算法1.map(key,value)

输入：全局变量centers，偏移量key，样本value

输出：<key’,value>对，其中key’是最近中心的索引，value’是样本信息的字符串

从value构造样本的instance；


minDis=Double.MAX_VALUE；
Index=-1；
For i=0 to centers.length do
dis=ComputeDist(instance,centers[i]);
If dis<minDis{
minDis=dis;
index=i;
}
End For

把index作为key’；

把不同维度的values构造成value’；

输出<key’,value’>对；

End

注意这里的Step 2和Step 3初始化了辅助变量minDis和index；Step 4通过计算找出了与样本最近的中心点，函数ComputeDist(instance,centers[i])返回样本和中心点centers[i]的距离；Step 8输出了用来进行下一个过程（combiner）的中间数据。

Combine函数. 每个map任务完成之后，我们用combiner去合并同一个map任务的中间结果。因为中间结果是存储在结点的本地磁盘上，所以这个过程不会耗费网络传输的代价。在combine函数中，我们把属于相同簇的values求和。为了计算每个簇的对象的平均值，我们需要记录每个map的每个簇中样本的总数。Combine函数的伪代码见算法2.

算法2.combine(key,V)

输入：key为簇的索引，V为属于该簇的样本列表

输出：<key’,value’>对，key’为簇的索引，value’是由属于同一类的所有样本总和以及样本数所组成的字符串。

初始化一个数组，用来记录同一类的所有样本的每个维度的总和，样本是V中的元素；

初始化一个计数器num为0来记录属于同一类的样本总数；

While(V.hasNext()){

从V.next()构造样本实例instance；

把instance的不同维度值相加到数组

num++;

}

把key作为key’；

构造value’：不同维度的求和结果+num；

输出<key’,value’>对；

End

Reduce函数. Reduce函数的输入数据由每个结点的combine函数获得。如combine函数所描述，输入数据包括部分样本（同一类）的求和以及对应样本数。在reduce函数中，我们可以把同一类的所有样本求和并且计算出对应的样本数。因此，我们可以得到用于下一轮迭代的新中心。Reduce函数的伪代码见算法3。

算法3.Reduce(key,V)

输入：key为簇的索引，V为来自不同结点的部分总和的样本列表

输出：<key’,value’>对，key’为簇的索引，value’是代表新的聚类中心的字符串

初始化一个数组，用来记录同一类的所有样本的每个维度的总和，样本是V中的元素；

初始化一个计数器NUM为0来记录属于同一类的样本总数；

While(V.hasNext()){

从V.next()构造样本实例instance；

把instance的不同维度值相加到数组

NUM+=num;

}

数组的每个元素除以NUM来获得新的中心坐标；

把key作为key’；

构造value’为所有中心坐标的字符串；

输出<key’,value’>对；

End

47.协同过滤中的算法怎么细分？

协同过滤算法通过对用户历史行为数据挖掘发现用户的偏好,基于不同的偏好对用户进行群组划分并推荐相似的商品。协同过的算法分为两类分为基于用户的协同过滤算法和基于物品的协同过滤的算法。基于用户的协同过滤是基于用户对物品的偏好找到相邻邻居用户然后将邻居用户喜欢的推荐给当前的用户。基于物品的协同过滤是计算邻居时采用物品本身,基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好推荐相似的物品给他。

48.FM公式

49. bagging和boosting的区别

Bagging是从训练集中进行子抽样组成每个基模型所需要的子训练集,然后对所有基模型预测的结果进行综合操作产生最终的预测结果。

Boosting中基模型按次序进行训练,而基模型的训练集按照某种策略每次都进行一定的转化,最后以一定的方式将基分类器组合成一个强分类器。

Bagging的训练集是在原始集中有放回的选取,而Boosting每轮的训练集不变,只是训练集中的每个样本在分类器中的权重都会发生变化,此权值会根据上一轮的结果进行调整。

Bagging的各个预测函数可以并行生成,Boosting的各预测函数只能顺序生成。

Bagging中整体模型的期望近似于基模型的期望,所以整体模型的偏差相似于基模型的偏差,因此Bagging中的基模型为强模型(强模型拥有低偏差高方差)。

Boosting中的基模型为弱模型,若不是弱模型会导致整体模型的方差很大。

50.XGBOOST和GDBT的区别：

GDBT在函数空间中利用梯度下降法进行优化而XGB在函数空间中使用了牛顿法进行优化。即GDBT在优化中使用了一阶导数信息,而XGB对损失函数进行了二阶泰勒展开,用到了一阶和二阶倒数信息。XGB在损失函数中加入了正则项(树叶子节点个数,每个叶子节点上输出score的L2模平方和。对于缺失的样本,XGB可以自动学习出它的分裂方向。GDBT的节点分裂方式使用的是gini系数,XGB通过优化推导出分裂前后的增益来选择分裂节点。XGB在处理每个特征列时可以做到并行。

51.GDBT的原理,以及常用的调参参数

先用一个初始值去学习一棵树,然后在叶子处得到预测值以及预测后的残差,之后的树则基于之前树的残差不断的拟合得到,从而训练出一系列的树作为模型。

n_estimators基学习器的最大迭代次数,learning_rate学习率，max_lead_nodes最大叶子节点数,max_depth树的最大深度,min_samples_leaf叶子节点上最少样本数。

52.stacking和blending的区别?

Stacking和blending的区别在于数据的划分,blending用不相交的数据训练不同的基模型,并将其输出取加权平均。而stacking是将数据集划分为两个不相交的集合,在第一个集合的数据集中训练多个模型,在第二个数据集中测试这些模型,将预测结果作为输入,将正确的标签作为输出,再训练一个高层的模型。

53.AdaBoost和GBDT的区别

AdaBoost通过调整错分的数据点的权重来改进模型,而GBDT是从负梯度的方向去拟合改进模型。

AdaBoost改变了训练数据的权值,即样本的概率分布,减少上一轮被正确分类的样本权值,提高被错误分类的样本权值,而随机森林在训练每棵树的时候,随机挑选部分训练集进行训练。在对新数据进行预测时,AdaBoost中所有树加权投票进行预测,每棵树的权重和错误率有关,而随机森林对所有树的结果按照少数服从多数的原则进行预测。

54. gbdt推导

GBDT 全称为 Gradient Boosting Decision Tree。顾名思义,它是一种基于决策树(decision tree)实现的分类回归算法。

Gradient Descent: method of steepest descent

梯度下降作为求解确定可微方程的常用方法而被人所熟知。它是一种迭代求解过程,具体就是使解沿着当前解所对应梯度的反方向迭代。这个方向也叫做最速下降方向。具体推导过程如下。假定当前已经迭代到第 k 轮结束,那么第 k+1 轮的结果怎么得到呢?我们对函数 f 做如下一阶泰勒展开：

为了使得第k+1 轮的函数值比第 k 轮的小,即如下不等式成立。

则只需使:

按照这样一直迭代下去,直到 ∇f(xk)=0, xk+1=xk ，函数收敛,迭代停止。由于在做泰勒展开时,要求xk+1−xk 足够小。因此,需要γ比较小才行,一般设置为 0~1 的小数。

顺带提一下,Gradient Descent 是一种一阶优化方法,为什么这么说呢?因为它在迭代过程中不需要二阶及以上的信息。如果我们在泰勒展开时,不是一阶展开,而是二阶展开。那对应的方法就是另一个被大家所熟知的可微方程求解方法:Newton Method,关于牛顿法的详细内容,我们会在后续文章介绍。

Boosting: Gradient Descent in functional space

Boosting一般作为一种模型组合方式存在,这也是它在 GBDT 中的作用。那Boosting 与 gradient descent 有什么关系呢?上一节我们说到 gradient descent 是一种确定可微方程的求解方法。这里的可微有一个要求,就是说上文中的损失函数 f 针对模型 x 直接可微。因此模型x可以根据梯度迭代直接求解。而这种损失函数针对模型直接可微是一个很强的假设,不是所有的模型都满足,比如说决策树模型。现在我们回到第一节,将f(x)写的更具体一点：

f(x)=l(h(x,D),Y)

其中D 为数据特征;Y 为数据 label;h 为模型函数,解决由 D->Y 的映射,x为模型函数参数,即通常我们说的模型;l 为目标函数或损失函数。

以逻辑回归为例, x为权重向量, h模型函数展开为:

目标函数l展开为:

我们发现函数1对h可微,同时h对x可微,因此l对x可微。因此,我们可以通过 gradient descent的方式对x进行直接求解,而不用将h保存下来。然而,如果l对h可微,但h对x不可微呢?我们仍按照第一节的方法先对l进行泰勒展开,只不过不是针对x,而是对 h。为了简单起见,我们省略D,Y。

其中:

按照第一节的逻辑,我们不难得出如下迭代公式:

但别忘了,我们的目的不是求 h,而是 x。由于 h 对 x 不可微,所以 x 必须根据数据重新学习得到。而此时我们重新学习 x 的目标已经不是源目标 Y,而是原损失函数 l 在当前 H 处的梯度,即:

这个重新学习x的过程正是每个base weak learner所做的事情。而这种通过weak learner 拟合每一步迭代后的梯度,进而实现weak learner组合的方式,就是Boosting。又由于我们在求导过程中,损失函数l没法对模型x直接求导,而只能对模型函数h求导。因此 Boosting又有一个别名:“函数空间梯度下降“。

此外,你可能会听过boosting的可加性(additive)。这里顺便提一句,可加性指的是 h 的可加,而不是x的可加。比如x是决策树,那两棵决策树本身怎么加在一起呢?你顶多把他们并排放在一起。可加的只是样本根据决策树模型得到的预测值 h(x,D)罢了。

Decision Tree: the based weak learner

Boosting 的本质就是使用每个weak learner来拟合截止到当前的梯度。则这里的D,还是原来数据中的D,而Y已经不是原来的Y了。而GBDT 中的这个weak learner 就是一棵分类回归树(CART)。因此我们可以使用决策树直接拟合梯度:∇l(H(xt))。此时我们要求的x就变成了这样一棵有k个叶子节点的、使得如下目标函数最小化的决策树:

其中T为目标∇l(H(xt)),W为每个叶子节点的权重,L为叶子节点集合。容易求得每个叶子节点的权重为归属到当前叶子节点的样本均值。即 :

每个样本的预测值即为其所归属的叶子节点的权重,即h(xt+1)

55.boosting和bagging在不同情况下的选用

Bagging与Boosting的区别：

1）取样方式（样本权重）：Bagging是均匀选取，样本的权重相等，Boosting根据错误率取样，错误率越大则权重越大。2）训练集的选择：Bagging随机选择训练集，训练集之间相互独立，Boosting的各轮训练集的选择与前面各轮的学习结果有关。3）预测函数：Bagging各个预测函数没有权重，可以并行生成，Boosting有权重，顺序生成。4）Bagging是减少variance，Boosting是减少bias。

Bagging 是 Bootstrap Aggregating的简称，意思就是再取样 (Bootstrap) 然后在每个样本上训练出来的模型取平均，所以是降低模型的 variance. Bagging 比如 Random Forest 这种先天并行的算法都有这个效果。

Boosting 则是迭代算法，每一次迭代都根据上一次迭代的预测结果对样本进行加权，所以随着迭代不不断进行行，误差会越来越小，所以模型的 bias 会不不断降低。这种算法无法并行。

56.rf和gbdt基分类器区别，里面的决策树分别长啥样，怎么剪枝？

GBDT和RF都是集成方法中的经典模型，我们需要弄清楚下面几个问题：1）GBDT是采用boosing方法，RF采用的是baggging方法；2）bias和variance是解释模型泛化性能的，其实还有噪声。

然后，理解GBDT和RF执行原理，其中GBDT中的核心是通过用分类器（如CART、RF）拟合损失函数梯度，而损失函数的定义就决定了在子区域内各个步长，其中就是期望输出与分类器预测输出的查，即bias；而RF的核心就是自采样（样本随机）和属性随机（所有样本中随机选择K个子样本选择最优属性来划分），样本数相同下的不同训练集产生的各个分类器，即数据的扰动导致模型学习性能的变化，即variance。

Gradient boosting Decision Tree(GBDT)

GB算法中最典型的基学习器是决策树，尤其是CART，正如名字的含义，GBDT是GB和DT的结合。要注意的是这里的决策树是回归树，GBDT中的决策树是个弱模型，深度较小一般不会超过5，叶子节点的数量也不会超过10，对于生成的每棵决策树乘上比较小的缩减系数（学习率<0.1），有些GBDT的实现加入了随机抽样（subsample 0.5<=f <=0.8）提高模型的泛化能力。通过交叉验证的方法选择最优的参数。

Random Forest：

bagging （你懂得，原本叫Bootstrap aggregating），bagging 的关键是重复的对经过bootstrapped采样来的观测集子集进行拟合。然后求平均。。。一个bagged tree充分利用近2/3的样本集。。。所以就有了OOB预估(outof bag estimation)

GBDT和随机森林的相同点：

1）都是由多棵树组成；2）最终的结果都是由多棵树一起决定

GBDT和随机森林的不同点：

1）组成随机森林的树可以是分类树，也可以是回归树；而GBDT只由回归树组成；

2）组成随机森林的树可以并行生成；而GBDT只能是串行生成；

3）对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来；

4）随机森林对异常值不敏感，GBDT对异常值非常敏感；

5）随机森林对训练集一视同仁，GBDT是基于权值的弱分类器的集成；

6）随机森林是通过减少模型方差提高性能，GBDT是通过减少模型偏差提高性能。

RF决策树：

学习随机森林模型前，一定要先了解决策树模型。树越深，模型越复杂。

决策树模型的优点如下。1）容易理解和解释，树可以被可视化。2）不需要太多的数据预处理工作，即不需要进行数据归一化，创造哑变量等操作。3）隐含地创造了多个联合特征，并能够解决非线性问题。

GBDT决策树：

迭代决策树GBDT（Gradient Boosting Decision Tree）也被称为是MART（Multiple Additive Regression Tree)）或者是GBRT（Gradient Boosting Regression Tree），也是一种基于集成思想的决策树模型，但是它和Random Forest有着本质上的区别。不得不提的是，GBDT是目前竞赛中最为常用的一种机器学习算法，因为它不仅可以适用于多种场景，更难能可贵的是，GBDT有着出众的准确率。

树的剪枝：

（1）前剪枝( Pre-Pruning)

通过提前停止树的构造来对决策树进行剪枝，一旦停止该节点下树的继续构造，该节点就成了叶节点。一般树的前剪枝原则有：a.节点达到完全纯度；b.树的深度达到用户所要的深度；c.节点中样本个数少于用户指定个数；d.不纯度指标下降的最大幅度小于用户指定的幅度。

（2）后剪枝( Post-Pruning)

首先构造完整的决策树，允许决策树过度拟合训练数据，然后对那些置信度不够的结点的子树用叶结点来替代。CART 采用Cost-Complexity Pruning（代价-复杂度剪枝法），代价(cost) ：主要指样本错分率；复杂度(complexity) ：主要指树t的叶节点数，(Breiman…)定义树t的代价复杂度(cost-complexity):信息熵H(X)，信息增益=H(D)-H(Y|X)，信息增益率=gain(x)/H(x)，Gini系数=1-sum（pk^2），基尼系数就是熵在x=1的地方一阶泰勒展开得到f(x)=1-x，所以gini=sum[x(1-x)]=1-sum(x^2)。

57.随机森林和 GBDT 的区别

1）随机森林采用的bagging思想，而GBDT采用的boosting思想。这两种方法都是Bootstrap思想的应用，Bootstrap是一种有放回的抽样方法思想。虽然都是有放回的抽样，但二者的区别在于：Bagging采用有放回的均匀取样，而Boosting根据错误率来取样（Boosting初始化时对每一个训练样例赋相等的权重1／n，然后用该算法对训练集训练t轮，每次训练后，对训练失败的样例赋以较大的权重），因此Boosting的分类精度要优于Bagging。Bagging的训练集的选择是随机的，各训练集之间相互独立，弱分类器可并行，而Boosting的训练集的选择与前一轮的学习结果有关，是串行的。2）组成随机森林的树可以是分类树，也可以是回归树；而GBDT只能由回归树组成。3）组成随机森林的树可以并行生成；而GBDT只能是串行生成。4）对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来。5）随机森林对异常值不敏感；GBDT对异常值非常敏感。6）随机森林对训练集一视同仁；GBDT是基于权值的弱分类器的集成。7）随机森林是通过减少模型方差提高性能；GBDT是通过减少模型偏差提高性能。

58.xgboost的特征重要性计算：

Xgboost根据结构分数的增益情况计算出来选择哪个特征作为分割点,而某个特征的重要性就是它在所有树中出现的次数之和。

59.xgboost的正则项表达式：

T为叶子节点的个数,w为叶子节点的分数

60.xgboost原理，怎么防过拟合？

XGBoost是一个树集成模型，它使用的是K（树的总数为K）个树的每棵树对样本的预测值的和作为该样本在XGBoost系统中的预测，定义函数如下：

对于所给的数据集有n个样本，m个特征，定义为：

其中Xi表示第i个样本，yi表示第i个样本的类别标签。CART树的空间为F，如下：

其中q表示每棵树的结构映射每个样本到相应的叶节点的分数，即q表示树的模型，输入一个样本，根据模型将样本映射到叶节点输出预测的分数；Wq(x)表示树q的所有叶节点的分数组成集合；T是树q的叶节点数量。

所以，由（1）式可以看出，XGBoost的预测值为每棵树的预测值之和，即每棵树相应的叶节点的得分之和（Wi的和，Wi表示第i个叶节点的得分）。

我们的目标就是学习这样的K个树模型f(x).。为了学习模型f(x)，我们定义下面的目标函数：

其中，（2）式右边第一项为损失函数项，即训练误差，是一个可微的凸函数（比如用于回归的均方误差和用于分类的Logistic误差函数等），第二项为正则化项，即每棵树的复杂度之和，目的是控制模型的复杂度，防止过拟合。我们的目标是在L(φ)取得最小化时得出对应的模型f(x)。

由于XGBoost模型中的优化参数是模型f(x)，不是一个具体的值，所以不能用传统的优化方法在欧式空间中进行优化，而是采用additive training的方式去学习模型。每一次保留原来的模型不变，加入一个新的函数f到模型中，如下：

预测值在每一次迭代中加入一个新的函数f目的是使目标函数尽量最大地降低。

因为我们的目标是最小化L(φ)时得到模型f(x)，但是L(φ)中并没有参数f(x)，所以，我们将上图中的最后一式代入L(φ)中可得到如下式子：

对于平方误差（用于回归）来说（3）式转换成如下形式：

对于不是平方误差的情况下，一般会采用泰勒展开式来定义一个近似的目标函数，以方便我们的进一步计算。

根据如下的泰勒展开式，移除高阶无穷小项，得：

（3）式等价于下面的式子：

由于我们的目标是求L(φ)最小化时的模型f(x)（也是变量），当移除常数项时模型的最小值变化，但是取最小值的变量不变（比如：y=x^2+C，无论C去何值，x都在0处取最小值）。所以，为了简化计算，我们移除常数项，得到如下的目标函数：

定义为叶节点j的实例，重写（4）式，将关于树模型的迭代转换为关于树的叶子节点的迭代，得到如下过程：

此时我们的目标是求每棵树的叶节点j的分数Wj，求出Wj后，将每棵树的Wj相加，即可得到最终的预测的分数。而要想得到最优的Wj的值，即最小化我们的目标函数，所以上式对Wj求偏导，并令偏导数为0，算出此时的W*j为：

将W*j代入原式得：

方程（5）可以用作得分(score)函数来测量树结构q的质量。该得分类似于评估决策树的不纯度得分，除了它是针对更广泛的目标函数得出的。

在xgboost调中，一般有两种方式用于控制过拟合：1）直接控制参数的复杂度：包括max_depth min_child_weight gamma；2）add randomness来使得对训练对噪声鲁棒。包括subsample colsample_bytree，或者也可以减小步长 eta，但是需要增加num_round，来平衡步长因子的减小。

61.xgboost，RF，LR优缺点场景

Xgboost：

优缺点：1）在寻找最佳分割点时，考虑传统的枚举每个特征的所有可能分割点的贪心法效率太低，xgboost实现了一种近似的算法。大致的思想是根据百分位法列举几个可能成为分割点的候选者，然后从候选者中根据上面求分割点的公式计算找出最佳的分割点。2）xgboost考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率，paper提到50倍。3）特征列排序后以块的形式存储在内存中，在迭代中可以重复使用；虽然boosting算法迭代必须串行，但是在处理每个特征列时可以做到并行。4）按照特征列方式存储能优化寻找最佳的分割点，但是当以行计算梯度数据时会导致内存的不连续访问，严重时会导致cache miss，降低算法效率。paper中提到，可先将数据收集到线程内部的buffer，然后再计算，提高算法的效率。5）xgboost 还考虑了当数据量比较大，内存不够时怎么有效的使用磁盘，主要是结合多线程、数据压缩、分片的方法，尽可能的提高算法的效率。

适用场景：分类回归问题都可以。

RF：

优点：1）表现性能好，与其他算法相比有着很大优势。2）随机森林能处理很高维度的数据（也就是很多特征的数据），并且不用做特征选择。3）在训练完之后，随机森林能给出哪些特征比较重要。4）训练速度快，容易做成并行化方法(训练时，树与树之间是相互独立的)。5）在训练过程中，能够检测到feature之间的影响。6）对于不平衡数据集来说，随机森林可以平衡误差。当存在分类不平衡的情况时，随机森林能提供平衡数据集误差的有效方法。7）如果有很大一部分的特征遗失，用RF算法仍然可以维持准确度。8）随机森林算法有很强的抗干扰能力（具体体现在6,7点）。所以当数据存在大量的数据缺失，用RF也是不错的。9）随机森林抗过拟合能力比较强（虽然理论上说随机森林不会产生过拟合现象，但是在现实中噪声是不能忽略的，增加树虽然能够减小过拟合，但没有办法完全消除过拟合，无论怎么增加树都不行，再说树的数目也不可能无限增加的）。10）随机森林能够解决分类与回归两种类型的问题，并在这两方面都有相当好的估计表现。（虽然RF能做回归问题，但通常都用RF来解决分类问题）。11）在创建随机森林时候，对generlization error(泛化误差)使用的是无偏估计模型，泛化能力强。

缺点：1）随机森林在解决回归问题时，并没有像它在分类中表现的那么好，这是因为它并不能给出一个连续的输出。当进行回归时，随机森林不能够做出超越训练集数据范围的预测，这可能导致在某些特定噪声的数据进行建模时出现过度拟合。（PS:随机森林已经被证明在某些噪音较大的分类或者回归问题上回过拟合）。2）对于许多统计建模者来说，随机森林给人的感觉就像一个黑盒子，你无法控制模型内部的运行。只能在不同的参数和随机种子之间进行尝试。3）可能有很多相似的决策树，掩盖了真实的结果。4）对于小数据或者低维数据（特征较少的数据），可能不能产生很好的分类。（处理高维数据，处理特征遗失数据，处理不平衡数据是随机森林的长处）。5）执行数据虽然比boosting等快（随机森林属于bagging），但比单只决策树慢多了。

适用场景：数据维度相对低（几十维），同时对准确性有较高要求时。因为不需要很多参数调整就可以达到不错的效果，基本上不知道用什么方法的时候都可以先试一下随机森林。

LR：

优点：实现简单，广泛的应用于工业问题上；分类时计算量非常小，速度很快，存储资源低；便利的观测样本概率分数；对逻辑回归而言，多重共线性并不是问题，它可以结合L2正则化来解决该问题。

缺点：当特征空间很大时，逻辑回归的性能不是很好；容易欠拟合，一般准确度不太高

不能很好地处理大量多类特征或变量；只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分；对于非线性特征，需要进行转换。

适用场景：LR同样是很多分类算法的基础组件，它的好处是输出值自然地落在0到1之间，并且有概率意义。因为它本质上是一个线性的分类器，所以处理不好特征之间相关的情况。虽然效果一般，却胜在模型清晰，背后的概率学经得住推敲。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。

62.xgboost特征并行化怎么做的？

决策树的学习最耗时的一个步骤就是对特征值进行排序,在进行节点分裂时需要计算每个特征的增益,最终选增益大的特征做分裂,各个特征的增益计算就可开启多线程进行。而且可以采用并行化的近似直方图算法进行节点分裂。

63.xgboost和lightgbm的区别和适用场景。

（1）xgboost采用的是level-wise的分裂策略，而lightGBM采用了leaf-wise的策略，区别是xgboost对每一层所有节点做无差别分裂，可能有些节点的增益非常小，对结果影响不大，但是xgboost也进行了分裂，带来了务必要的开销。 leaft-wise的做法是在当前所有叶子节点中选择分裂收益最大的节点进行分裂，如此递归进行，很明显leaf-wise这种做法容易过拟合，因为容易陷入比较高的深度中，因此需要对最大深度做限制，从而避免过拟合。

（2）lightgbm使用了基于histogram的决策树算法，这一点不同与xgboost中的 exact 算法，histogram算法在内存和计算代价上都有不小优势。1）内存上优势：很明显，直方图算法的内存消耗为(#data* #features * 1Bytes)(因为对特征分桶后只需保存特征离散化之后的值)，而xgboost的exact算法内存消耗为：(2 * #data * #features* 4Bytes)，因为xgboost既要保存原始feature的值，也要保存这个值的顺序索引，这些值需要32位的浮点数来保存。2）计算上的优势，预排序算法在选择好分裂特征计算分裂收益时需要遍历所有样本的特征值，时间为(#data),而直方图算法只需要遍历桶就行了，时间为(#bin)

（3）直方图做差加速，一个子节点的直方图可以通过父节点的直方图减去兄弟节点的直方图得到，从而加速计算。

（4）lightgbm支持直接输入categorical 的feature，在对离散特征分裂时，每个取值都当作一个桶，分裂时的增益算的是”是否属于某个category“的gain。类似于one-hot编码。

（5）xgboost在每一层都动态构建直方图，因为xgboost的直方图算法不是针对某个特定的feature，而是所有feature共享一个直方图(每个样本的权重是二阶导),所以每一层都要重新构建直方图，而lightgbm中对每个特征都有一个直方图，所以构建一次直方图就够了。

64.HMM隐马尔可夫模型的参数估计方法是？

EM算法

解析：期望最大化（Expectation-Maximum,EM）算法

65.Bootstrap方法是什么？

从一个数据集中有放回的抽取N次，每次抽M个。

解析：Bagging算法基于bootstrap。面试时结合Bagging算法讲述会更好。

66.如何防止过拟合？

1.早停法；2.l1和l2正则化；3.神经网络的dropout；4.决策树剪枝；5.SVM的松弛变量；6.集成学习

解析：能够达到模型权重减小，模型简单的效果

67. EM算法推导，jensen不等式确定的下界

给定的训练样本是，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大。p(x,z)的最大似然估计如下：

第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。

EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化，我们可以不断地建立的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。

对于每一个样例i，让表示该样例隐含变量z的某种分布，满足的条件是。（如果z是连续性的，那么是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。

可以由前面阐述的内容得到下面的公式：

（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式，考虑到是凹函数（二阶导数小于0），而且

就是的期望（回想期望公式中的Lazy Statistician规则）

设Y是随机变量X的函数（g是连续函数），那么

（1） X是离散型随机变量，它的分布律为，k=1,2,…。若绝对收敛，则有

（2） X是连续型随机变量，它的概率密度为，若绝对收敛，则有

对应于上述问题，Y是，X是，是，g是到的映射。这样解释了式子（2）中的期望，再根据凹函数时的Jensen不等式：

可以得到（3）。

这个过程可以看作是对求了下界。对于的选择，有多种可能，那种更好的？假设已经给定，那么的值就决定于和了。我们可以通过调整这两个概率使下界不断上升，以逼近的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

c为常数，不依赖于。对此式子做进一步推导，我们知道，那么也就有，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式：

至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。接下来的M步，就是在给定后，调整，去极大化的下界（在固定后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：

循环重复直到收敛{

（E步）对于每一个i，计算

（M步）计算

那么究竟怎么确保EM收敛？假定和是EM第t次和t+1次迭代后的结果。如果我们证明了，也就是说极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。下面来证明，选定后，我们得到E步

这一步保证了在给定时，Jensen不等式中的等式成立，也就是

然后进行M步，固定，并将视作变量，对上面的求导后，得到，这样经过一些推导会有以下式子成立：

解释第（4）步，得到时，只是最大化，也就是的下界，而没有使等式成立，等式成立只有是在固定，并按E步得到时才能成立。

况且根据我们前面得到的下式，对于所有的和都成立

第（5）步利用了M步的定义，M步就是将调整到，使得下界最大化。因此（5）成立，（6）是之前的等式结果。这样就证明了会单调增加。一种收敛方法是不再变化，还有一种就是变化幅度很小。

再次解释一下（4）、（5）、（6）。首先（4）对所有的参数都满足，而其等式成立条件只是在固定，并调整好Q时成立，而第（4）步只是固定Q，调整，不能保证等式一定成立。（4）到（5）就是M步的定义，（5）到（6）是前面E步所保证等式成立条件。也就是说E步会将下界拉到与一个特定值（这里）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与另外一个特定值一样的高度，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到最大值。

如果我们定义

从前面的推导中我们知，EM可以看作是J的坐标上升法，E步固定，优化，M步固定。优化

Jensen不等式表述如下：

如果f是凸函数，X是随机变量，那么：，特别地，如果f是严格凸函数，当且

仅当X是常量时，上式取等号。所以其下界是。

68.Focal Loss

Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

损失函数形式：Focal loss是在交叉熵损失函数基础上进行的修改，首先回顾二分类交叉上损失：

是经过激活函数的输出，所以在0-1之间。可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。

首先在原有的基础上加了一个因子，其中gamma>0使得减少易分类样本的损失。使得更关注于困难的、错分的样本。

例如gamma为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的gamma次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。

此外，加入平衡因子alpha，用来平衡正负样本本身的比例不均：

只添加alpha虽然可以平衡正负样本的重要性，但是无法解决简单与困难样本的问题。

lambda调节简单样本权重降低的速率，当lambda为0时即为交叉熵损失函数，当lambda增加时，调整因子的影响也在增加。实验发现lambda为2是最优。

69.方差偏差的分解公式

为模型的方差

为模型的偏差

为模型的噪声

为训练集D上学得模型f在x上的输出

为模型的期望预测

70.对应时间序列的数据集如何进行交叉验证？

1.预测后一半；2.日向前链

解析：传统的交叉验证由于假定样本独立同分布，因此随机打乱分为训练集和验证集。但是对于时间序列来讲，需要考虑序列间的时间依赖。

71.正负样本不平衡的解决办法？评价指标的参考价值？

上下采样法。

好的指标：ROC和AUC、F值、G-Mean；不好的指标：Precision、Recall

72.迁移学习

迁移学习就是把之前训练好的模型直接拿来用，可以充分利用之前数据信息，而且能够避免自己实验数据量较小等问题。简单来讲就是给模型做初始化，初始化的数据来自于训练好的模型。

73.数据不平衡怎么办?

使用正确的评估标准,当数据不平衡时可以采用精度,调用度,F1得分,MCC,AUC等评估指标。

重新采样数据集,如欠采样和过采样。欠采样通过减少冗余类的大小来平衡数据集。当数据量不足时采用过采样,尝试通过增加稀有样本的数量来平衡数据集,通过使用重复,自举,SMOTE等方法生成新的样本。

以正确的方式使用K-fold交叉验证,组合不同的重采样数据集,对多数类进行聚类。

74.AUC：

Auc体现出容忍样本倾斜的能力,只反应模型对正负样本排序能力的强弱,而其直观含以上是任意取一个正样本和负样本,正样本的得分大于负样本的概率。

M为正样本数,N为负样本数。Rank的值代表能够产生前大后小这样的组合数,但是其中包含了(正,正)的情况,所以要减去正例的个数所以可得上述公式。

75.生成模型和判别模型的区别

生成模型是先从数据中学习联合概率分布,然后利用贝叶斯公式求得特征和标签对应的条件概率分布。判别模型直接学习条件概率分布,直观的输入什么特征就预测可能的类别。

76.特征选择怎么做

特征选择是一个重要的数据预处理过程，主要有两个原因：一是减少特征数量、降维，使模型泛化能力更强，减少过拟合;二是增强对特征和特征值之间的理解。

常见的特征选择方式：

1）去除方差较小的特征

2）正则化。L1正则化能够生成稀疏的模型。L2正则化的表现更加稳定，由于有用的特征往往对应系数非零。

3）随机森林，对于分类问题，通常采用基尼不纯度或者信息增益，对于回归问题，通常采用的是方差或者最小二乘拟合。一般不需要feature engineering、调参等繁琐的步骤。它的两个主要问题，1是重要的特征有可能得分很低（关联特征问题），2是这种方法对特征变量类别多的特征越有利（偏向问题）。

4）稳定性选择。是一种基于二次抽样和选择算法相结合较新的方法，选择算法可以是回归、SVM或其他类似的方法。它的主要思想是在不同的数据子集和特征子集上运行特征选择算法，不断的重复，最终汇总特征选择结果，比如可以统计某个特征被认为是重要特征的频率（被选为重要特征的次数除以它所在的子集被测试的次数）。理想情况下，重要特征的得分会接近100%。稍微弱一点的特征得分会是非0的数，而最无用的特征得分将会接近于0。

77. ID3树用什么指标选择特征

基于信息增益最大的作为最优特征，以此为决策树的根节点

78.特征工程的问题

特征工程包括数据与特征处理、特征选择和降纬三部分。数据与特征处理包括：

1.数据选择、清洗、采样

数据格式化；

数据清洗，填充缺失值、去掉脏数据，将不可信的样本丢掉，缺省值极多的字段考虑不用；

采样：针对正负样本不平衡的情况，当正样本远大于负样本时，且量都很大时，使用下采样，量不大时，可采集更多的数据或oversampling或修改损失函数；采样过程中可利用分层抽样保持不同类别数据的比例。

2.不同类型数据的特征处理

数值型：幅度调整/归一化、log等变化、统计值（例如max、min、mean、std）、离散化、分桶等

类别型：one-hot编码等

时间型：提取出连续值的持续时间和间隔时间；提取出离散值的“年”、“月”、“日”、“一年中哪个星期/季度”、“一周中的星期几”、“工作日/周末”等信息

文本型：使用If-idf特征

统计型：加减平均、分位线、次序、比例

意义：

对数据进行预处理，可提高数据质量，提高挖掘质量。对数据进行清洗可填充缺失值、光滑噪声数据，识别和删除离群点数据，保证数据的一致性；

使用正确的采样方法可解决因数据不平衡带来的预测偏差；

对不同的数据类型进行不同的特征处理有助于提高特征的可用性，例如对数值型数据进行归一化可将数据转化到统一量纲下；对类别型数据，可用one-hot编码方法将类别数据数字化，数字化特征之后可更用来计算距离、相似性等；可从时间型数据当中提取中更多的时间特征，例如年、月和日等，这些特征对于业务场景以及模型的预测往往有很大的帮助。统计型特征处理有助于从业务场景中挖掘更丰富的信息。

特征选择包括：

1.Filter：使用方差、Pearson相关系数、互信息等方法过滤特征，评估单个特征和结果值之间的相关程度，留下Top相关的特征部分。

2.Wrapper：可利用“递归特征删除算法”，把特征选择看做一个特征子集搜索问题，筛选各种特征子集，用模型评估效果。

3.Embedded：可利用正则化方式选择特征，使用带惩罚项的基模型，除了选择出特征外，同时也进行了降纬。

意义：

-剔除对结果预测不大的特征，减小冗余，选择有意义的特征输入模型，提高计算性能。

降维：

方法：主成分分析法（PCA）和线性判别分析（LDA）

意义：通过PCA或LDA方法，将较高纬度样本空间映射到较低维度的样本空间，从而达到降纬的目的，减少模型的训练时间，提高模型的计算性能。

79.给了个链接线上写代码，要求写读文本、文本预处理、特征提取和建模的基本过程，不过写到特征就没写了

收集数据

总所周知，数据挖掘模型中非常重要的部分是训练模型，训练集与测试集便是整个数据挖掘过程中花费时间最多的过程。数据集通过有如下的一些途径获得：

经典数据集：Python NLTK 便提供了非常多经典的数据集。很多数据集都是手工标注而成，所以使用的时候不得不感叹工程的浩大。例如NLP中使用的Penn TreeBank，有兴趣的同学可以看看他们的论文《Building a Large Annotated Corpus of English: The Penn TreeBank》，那简直就是一部辛酸史啊！

从网页上抓取：直接动手写一个爬虫爬取特定的网页不难，通过正则表达式就能够将有效的内容提取出来；当然，发扬拿来主义精神的话，我们可以使用Python中一些优秀的库，比如scrapy，beautifulsoup 等等。

从日志、已有文件中分析：如果是海量数据的话可以使用hadoop这样的系统。结合传统SQL中的一些特殊功能，例如Partition，有时会有不错的效果，不过最多压缩空间、缩减特征再用SQL处理。

其他网络数据集：Stanford Large Network Dataset Collectionm，100+ Interesting Data Sets for Statistics

预处理

如果是网页内容，首先需要去掉Html Tag，lxml和html5lib是比较有名的Python库，beautifulsoup也对他们做了一层封装。不过别忘了，Python本身也自带了sgmllib这样的基本可扩展的解析器。如果是有特别的处理，其实正则表达式也是不错的选择。

处理编码，由于我主要是处理英文的数据，这一步基本也跳过了。

将文档分割成句子（可选）。很多时候我们采用的是词袋模型（bag of words），所以是否分割成句子也无所谓。比较简单的方法就是Python NLTK中的sent_tokenize()函数，用的是punkt算法，论文在这里。

将句子分割成词。首先用正则表达式可以自己完成；如果要利用已有工具，Python NLTK中的word_tokenize()，这个方式就是前文提到的Penn TreeBank语料库所使用的分词方法。听起来是不是很高大上，我是不会告诉你其实它也是正则表达式实现的，想知道具体实现，戳这里。分词其实主要干了这么几个事：1）将’分开. don't -> do n't, they'll -> they 'll; 2）将大部分标点当作单独的一个词; 3）将后一位是逗号或者引号的词分开; 4）单独出现在一行的句号分开。中文分词区别比较大，可以采用斯坦福或者ICTCLAS（中科院背景）的方案。

拼写错误纠正。推荐pyenchant，非常喜欢，因为简洁到四句语句就能完成。Windows 8中操作系统也直接提供了拼写检查的COM端口，不过就得多花时间研究啦。

POS Tagging（根据实际应用）。还是Nltk，首页就有介绍；斯坦福也提供了这类工具。这一块属于NLP的范畴，还是Parsing等应用，要了解NLP原理推荐Coursera上一门不错的课程Natural Language Processing

去掉标点。正则表达式即可，有的时间非常短的单词也可以一起去掉，len<3的常见的选择

去掉非英文字符的词（根据实际应用决定）。

转换成小写。

去掉停用词。就是在各种句子中都经常出现的一些词，I、and什么的。NLTK有一个Stopwords。Matthew L. Jockers提供了一份比机器学习和自然语言处理中常用的停词表更长的停词表。中文停用词戳这里。什么？你问我停用词怎么找到的，我想大概是IDF这样的算法吧。

词型转换。简单来讲，我们希望do、did、done都能统一的返回do。第一种方法叫stem，Porter是比较常见的一种基于规则的算法，网页有snowball工具，也是它的论文。Porter的结果差强人意，单词末尾有e、y的，基本上stem之后都不间了，例如replace->replac；末尾有重复单词的，基本只剩一个了，例如ill->il。NLTK中也有Stem库，算法应该是类似的。第二种方法叫lemmatization，就是基于词典做词型转换，NLTK的Stem库中便有WordNetLemmatizer可以使用。

去掉长度过小的词（可选）。如果之前做了，这里要再做一次，因为stem会改变词型。

重新去停用词。理由同上。

特征提取：

1、TF-IDF：

2、词频方法(Word Frequency)：

3、文档频次方法(Document Frequency)：

4、互信息(Mutual Information)：

5、期望交叉熵(Expected Cross Entropy)：

6、二次信息熵(QEMI)：

7、信息增益方法(Information Gain)：

8、x2统计量方法：

9、文本证据权(The Weight of Evidence forText)：

10、优势率(Odds Ratio)：

11、遗传算法(Genetic Algorithm, GA)：

12、主成分分析法(Principal Component Analysis，PCA)：

13、模拟退火算法(Simulating Anneal，SA)：

14、N—Gram算法

文本建模：

LDA、pLSA、LSA

80.softmax公式：

考虑一个多分类问题，即预测变量y可以取k个离散值中的任何一个.比如一个邮件分类系统将邮件分为私人邮件，工作邮件和垃圾邮件。由于y仍然是一个离散值，只是相对于二分类的逻辑回归多了一些类别。下面将根据多项式分布建模。

考虑将样本共有k类，每一类的概率分别为,由于，所以通常我们只需要k-1个参数即可

，

为了推导，引入表达式：

上面T(y)是k-1维列向量,其中y = 1, 2, ...k.

T(y)i 表示向量T(y)的第i个元素。

还要引入表达式,如果大括号里面为真，则真个表达式就为1，否则为0.例如：1{2=3} = 0和1{3=3} = 1.

则上面的k个向量就可以表示为

以为y只能属于某一个类别，于是T(y)中只能有一个元素为1其他元素都为0，可以求出k-1个元素的期望：

定义：

其中i = 1,2,...k.则有：

也就容易得出：，由该式和上面使得等式：一起可以得到：这个函数就是softmax函数。

然后假设和具有线性关系，即

于是从概率的角度出发：

其中这个模型就是softmax回归（softmax regression）, 它是逻辑回归的泛化。

这样我们的输出：

就是输出了x属于（1,2,...k-1）中每一类的概率，当然属于第k类的概率就是：

下面开始拟合参数

同样使用最大化参数θ的对数似然函数：

这里使用梯度下降和牛顿法均可。

81、softmax公式

参考回答：

考虑将样本共有k类，每一类的概率分别为,由于，所以通常我们只需要k-1个参数即可

，

为了推导，引入表达式：

上面T(y)是k-1维列向量,其中y = 1, 2, ...k.

T(y)i 表示向量T(y)的第i个元素。

还要引入表达式,如果大括号里面为真，则真个表达式就为1，否则为0.例如：1{2=3} = 0和1{3=3} = 1.

则上面的k个向量就可以表示为

以为y只能属于某一个类别，于是T(y)中只能有一个元素为1其他元素都为0，可以求出k-1个元素的期望：

定义：

其中i = 1,2,...k.则有：

也

就容易得出：，由该式和上面使得等式：一起可以得到：这个函数就是softmax函数。

然后假设和具有线性关系，即

于是从概率的角度出发：

其中这个模型就是softmax回归（softmax regression）, 它是逻辑回归的泛化。

这样我们的输出：

就是输出了x属于（1,2,...k-1）中每一类的概率，当然属于第k类的概率就是：

下面开始拟合参数

同样使用最大化参数θ的对数似然函数：

这里使用梯度下降和牛顿法均可。

82、检测20类物体，多少张训练集，怎么训练？

多分类问题，保证各类别的样例比，提取特征，用libsvm等做多分类。

83.lightgbm优势

1）更快的训练速度和更高的效率：LightGBM使用基于直方图的算法。2）更低的内存占用：使用离散的箱子(bins)保存并替换连续值导致更少的内存占用。3）更高的准确率(相比于其他任何提升算法)：它通过leaf-wise分裂方法产生比level-wise分裂方法更复杂的树，这就是实现更高准确率的主要因素。然而，它有时候或导致过拟合，但是我们可以通过设置|max-depth|参数来防止过拟合的发生。4）大数据处理能力：相比于XGBoost，由于它在训练时间上的缩减，它同样能够具有处理大数据的能力。5）支持并行学习。

84.MXNet和Tensorflow的区别

MXNet有两个主要的进程server和worker,worker之间不能进行通信,只能通过server互相影响。Tensorflow有worker,server,client三种进程,worker是可以相互通信的,可以根据op的依赖关系主动收发数据。MXNet常用来做数据并行,每个GPU设备上包含了计算图中所有的op,而Tensorflow可以由用户指定op的放置,一般情况下一个GPU设备负责某个和几个op的训练任务。

85. Tensorflow的工作原理

Tensorflow是用数据流图来进行数值计算的,而数据流图是描述有向图的数值计算过程。在有向图中,节点表示为数学运算,边表示传输多维数据,节点也可以被分配到计算设备上从而并行的执行操作。

86.Tensorflow中interactivesession和session的区别：

Tf. Interactivesession()默认自己就是用户要操作的会话,而tf.Session()没有这个默认,所以eval()启动计算时需要指明使用的是哪个会话。

二、深度学习（计算机视觉，重视业务）（50%）

1.深度学习知识体系：

2.张量（tensor）是什么？关于张量？

张量=数据容器。多数情况下，它包含数字，有时候它也包含字符串，但这种情况比较少。因此把它想象成一个数字的水桶。

0维到5维的张量如下图（0维张量-数字，1维张量-向量，2维张量-矩阵，3维张量-照片，4维张量-照片集）：

3.卷积神经网络的意义？本质是什么东西？试解释清楚以下神经网络结构？

4.BatchNormalization的作用：

神经网络在训练的时候随着网络层数的加深,激活函数的输入值的整体分布逐渐往激活函数的取值区间上下限靠近,从而导致在反向传播时低层的神经网络的梯度消失。而BatchNormalization的作用是通过规范化的手段,将越来越偏的分布拉回到标准化的分布,使得激活函数的输入值落在激活函数对输入比较敏感的区域,从而使梯度变大,加快学习收敛速度,避免梯度消失的问题。

5.梯度消失：

在神经网络中，当前面隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降了。这种现象叫做消失的梯度问题。

6.循环神经网络，为什么好?

循环神经网络模型（RNN）是一种节点定向连接成环的人工神经网络，是一种反馈神经网络，RNN利用内部的记忆来处理任意时序的输入序列，并且在其处理单元之间既有内部的反馈连接又有前馈连接，这使得RNN可以更加容易处理不分段的文本等。

7.什么是Group Convolution？

若卷积神将网络的上一层有N个卷积核,则对应的通道数也为N。设群数目为M,在进行卷积操作的时候,将通道分成M份,每个group对应N/M个通道,然后每个group卷积完成后输出叠在一起,作为当前层的输出通道。

8、什么是RNN

一个序列当前的输出与前面的输出也有关,在RNN网络结构中中,隐藏层的输入不仅包括输入层的输出还包含上一时刻隐藏层的输出,网络会对之前的信息进行记忆并应用于当前的输入计算中。

9、训练过程中,若一个模型不收敛,那么是否说明这个模型无效?导致模型不收敛的原因有哪些?

并不能说明这个模型无效,导致模型不收敛的原因可能有数据分类的标注不准确,样本的信息量太大导致模型不足以fit整个样本空间。学习率设置的太大容易产生震荡,太小会导致不收敛。可能复杂的分类任务用了简单的模型。数据没有进行归一化的操作。

10.图像处理中锐化和平滑的操作

锐化就是通过增强高频分量来减少图像中的模糊,在增强图像边缘的同时也增加了图像的噪声。

平滑与锐化相反,过滤掉高频分量,减少图像的噪声是图片变得模糊。

11. VGG使用3*3卷积核的优势是什么?

2个3*3的卷积核串联和5*5的卷积核有相同的感知野,前者拥有更少的参数。多个3*3的卷积核比一个较大尺寸的卷积核有更多层的非线性函数,增加了非线性表达,使判决函数更具有判决性。

12.Relu比Sigmoid的效果好在哪里?

Sigmoid的导数只有在0的附近时有较好的激活性,而在正负饱和区域的梯度趋向于0,从而产生梯度弥散的现象,而relu在大于0的部分梯度为常数,所以不会有梯度弥散现象。Relu的导数计算的更快。Relu在负半区的导数为0,所以神经元激活值为负时,梯度为0,此神经元不参与训练,具有稀疏性。

13. 神经网络中权重共享的是？

卷积神经网络、循环神经网络

解析：通过网络结构直接解释

14.神经网络激活函数？

sigmod、tanh、relu

解析：需要掌握函数图像，特点，互相比较，优缺点以及改进方法

15.在深度学习中，通常会finetuning已有的成熟模型，再基于新数据，修改最后几层神经网络权值，为什么？

实践中的数据集质量参差不齐，可以使用训练好的网络来进行提取特征。把训练好的网络当做特征提取器。

16.画GRU结构图：

GRU有两个门：更新门，输出门

解析：如果不会画GRU，可以画LSTM或者RNN。再或者可以讲解GRU与其他两个网络的联系和区别。不要直接就说不会。

17.Attention机制的作用

减少处理高维输入数据的计算负担,结构化的选取输入的子集,从而降低数据的维度。让系统更加容易的找到输入的数据中与当前输出信息相关的有用信息,从而提高输出的质量。帮助类似于decoder这样的模型框架更好的学到多种内容模态之间的相互关系。

18.Lstm和Gru的原理

Lstm由输入门,遗忘门,输出门和一个cell组成。第一步是决定从cell状态中丢弃什么信息,然后在决定有多少新的信息进入到cell状态中,最终基于目前的cell状态决定输出什么样的信息。

Gru由重置门和跟新门组成,其输入为前一时刻隐藏层的输出和当前的输入,输出为下一时刻隐藏层的信息。重置门用来计算候选隐藏层的输出,其作用是控制保留多少前一时刻的隐藏层。跟新门的作用是控制加入多少候选隐藏层的输出信息,从而得到当前隐藏层的输出。

19.什么是dropou

在神经网络的训练过程中,对于神经单元按一定的概率将其随机从网络中丢弃,从而达到对于每个mini-batch都是在训练不同网络的效果,防止过拟合。

20. LSTM每个门的计算公式

遗忘门:

输入门:

输出门:

21. DropConnect的原理

防止过拟合方法的一种,与dropout不同的是,它不是按概率将隐藏层的节点输出清0,而是对每个节点与之相连的输入权值以一定的概率清0。

22. 深度学习了解多少，有看过底层代码吗？caffe,tf?

23. 除了GMM-HMM，你了解深度学习在语音识别中的应用吗？

讲了我用的过DNN-HMM，以及与GMM-HMM的联系与区别；然后RNN+CTC，这里我只是了解，大概讲了一下CTC损失的原理；然后提了一下CNN+LSTM。

24.用过哪些移动端深度学习框架？

开源的有：小米的MACE，骁龙的SNPE，腾讯的FeatherCNN和ncnn，百度的mobile-deep-learning(MDL)；caffe、tensorflow lite都有移动端，只是可能没有上面的框架效率高。据传还有支付宝的xNN，商汤的PPL，不过都是自用，未开源。

25.Caffe：整体架构说一下，新加一个层需要哪些步骤，卷积是怎么实现的，多卡机制，数据并行还是模型并行？

Caffe是深度学习的一个框架，Caffe框架主要包括五个组件：Blob、Solver、Net、Layer、Proto；框架结构如下图所示。这五大组件可以分为两个部分：第一部分，Blob、Layer和Net，这三个组件使得Caffe构成基于自己的模块化的模型，caffe是逐层地定义一个net，而net是从数据输入层到损失曾自下而上定义整个模型，Blob在caffe中是处理和传递实际数据的数据封装包；第二部分：Solver和Proto，这两个模型分别用于协调模型的优化以及用于网络模型的结构定义、存储和读取的方式（Layer-By-Layer）定义Net，而贯穿所有Nets的结构就是caffe框架或模型；对于Layer而言，输入的是Blob数据封装包格式的实际数据，当采用该框架进行训练时，也就是Solver调优模型，则需要Proto这种网络模型的结构定义、存储和读取。

总体来说，caffe是通过Layer

Caffe中卷积运算的原理

俗话说，一图胜千言，首先先给出原理示意图，为了方便理解，这里以二维核为例

滑动窗口在图像中每滑动一个地方，将图像中该滑动窗口图像展开为一列，所有列组成图中的滑动窗口矩阵，这里假设pad=1,stride=1,K=3,则滑动窗口矩阵每行大小为W*H,一共K*K行.

每个核展开为一行，N个核形成的核矩阵大小为N*K*K。

最后将核矩阵和滑动窗口矩阵相乘，每一行就是一个特征图，N个卷积核形成N个特征图。

扩展到三维核

三维核就是多了一个通道的概念，原理与二维核一样。

caffe支持多GPU并行了，原理比较简单，就是每个GPU分别算一个batch，n个GPU，实际的batchsize就是n*batch，比如原来用一个GPU，batchsize设置成256，现在用4个GPU，把batchsize设置成64，和原来的一个GPU的运算是等价的。

实际使用的时候基本不用设置，和原来一样编译好就可以用了。命令就是在-gpu 后面对多个GPU号用逗号隔开，比如-gpu 1,2,3,4 就是同时使用1-4共4个GPU，GPU编号可以不连续，或者直接用-gpu all，就是使用所有的GPU。

Caffe是数据并行的。

26.BN层的作用，为什么要在后面加伽马和贝塔，不加可以吗

BN层的作用是把一个batch内的所有数据，从不规范的分布拉到正态分布。这样做的好处是使得数据能够分布在激活函数的敏感区域，敏感区域即为梯度较大的区域，因此在反向传播的时候能够较快反馈误差传播。

27.梯度消失，梯度爆炸的问题，

激活函数的原因，由于梯度求导的过程中梯度非常小，无法有效反向传播误差，造成梯度消失的问题。

28.Adam

Adam 算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率（即 alpha）更新所有的权重，学习率在训练过程中并不会改变。而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。

29.attention机制

Attention简单理解就是权重分配，。以seq2seq中的attention公式作为讲解。就是对输入的每个词分配一个权重，权重的计算方式为与解码端的隐含层时刻作比较，得到的权重的意义就是权重越大，该词越重要。最终加权求和。

30.RNN梯度消失问题,为什么LSTM和GRU可以解决此问题

RNN由于网络较深,后面层的输出误差很难影响到前面层的计算,RNN的某一单元主要受它附近单元的影响。而LSTM因为可以通过阀门记忆一些长期的信息,相应的也就保留了更多的梯度。而GRU也可通过重置和更新两个阀门保留长期的记忆,也相对解决了梯度消失的问题。

31.GAN网络的思想

GAN用一个生成模型和一个判别模型,判别模型用于判断给定的图片是不是真实的图片,生成模型自己生成一张图片和想要的图片很像,开始时两个模型都没有训练,然后两个模型一起进行对抗训练,生成模型产生图片去欺骗判别模型,判别模型去判别真假,最终两个模型在训练过程中,能力越来越强最终达到稳态。

32.1*1的卷积作用

实现跨通道的交互和信息整合,实现卷积核通道数的降维和升维,可以实现多个feature map的线性组合,而且可是实现与全连接层的等价效果。

33.怎么提升网络的泛化能力

从数据上提升性能:收集更多的数据,对数据做缩放和变换,特征组合和重新定义问题。

从算法调优上提升性能:用可靠的模型诊断工具对模型进行诊断,权重的初始化,用小的随机数初始化权重。对学习率进行调节,尝试选择合适的激活函数,调整网络的拓扑结构,调节batch和epoch的大小,添加正则化的方法,尝试使用其它的优化方法,使用early stopping。

34.什么是seq2seq model

Seq2seq属于encoder-decoder结构的一种,利用两个RNN,一个作为encoder一个作为decoder。Encoder负责将输入序列压缩成指定长度的向量,这个向量可以看作这段序列的语义,而decoder负责根据语义向量生成指定的序列。

35.激活函数的作用

激活函数是用来加入非线性因素的,提高神经网络对模型的表达能力,解决线性模型所不能解决的问题。

36. 为什么用relu就不用sigmoid了？

Sigmoid的导数只有在0的附近时有比较好的激活性,在正负饱和区域的梯度都接近0，会导致梯度弥散。而relu函数在大于0的部分梯度为常数,不会产生梯度弥散现象。Relu函数在负半区导数为0,也就是说这个神经元不会经历训练,就是所谓稀疏性。而且relu函数的导数计算的更快。

37.讲一下基于WFST的静态解码网络的语音识别流程？

从语音特征开始讲起，我讲了MFCC和LPC的原理以及提取过程，这一部分讲的很细，然后讲了viterbi解码过程，最后概述了一下HCLG.fst构建流程

38.目标检测了解吗，Faster RCNN跟RCNN有什么区别？

目标检测，也叫目标提取，是一种基于目标几何和统计特征的图像分割，它将目标的分割和识别合二为一，其准确性和实时性是整个系统的一项重要能力。尤其是在复杂场景中，需要对多个目标进行实时处理时，目标自动提取和识别就显得特别重要。

随着计算机技术的发展和计算机视觉原理的广泛应用，利用计算机图像处理技术对目标进行实时跟踪研究越来越热门，对目标进行动态实时跟踪定位在智能化交通系统、智能监控系统、军事目标检测及医学导航手术中手术器械定位等方面具有广泛的应用价值。

39.SPP，YOLO了解吗？

SPP-Net简介：

SPP-Net主要改进有下面两个：

1）.共享卷积计算、2）.空间金字塔池化

在SPP-Net中同样由这几个部分组成：

ss算法、CNN网络、SVM分类器、bounding box

ss算法的区域建议框同样在原图上生成，但是却在Conv5上提取，当然由于尺寸的变化，在Conv5层上提取时要经过尺度变换，这是它R-CNN最大的不同，也是SPP-Net能够大幅缩短时长的原因。因为它充分利用了卷积计算，也就是每张图片只卷积一次，但是这种改进带来了一个新的问题，由于ss算法生成的推荐框尺度是不一致的，所以在cov5上提取到的特征尺度也是不一致的，这样是没有办法做全尺寸卷积的（Alexnet）。

所以SPP-Net需要一种算法，这种算法能够把不一致的输入产生统一的输出，这就SPP，即空间金字塔池化，由它替换R-CNN中的pooling层，除此之外，它和R-CNN就一样了。

YOLO详解：

YOLO的名字You only look once正是自身特点的高度概括。YOLO的核心思想在于将目标检测作为回归问题解决，YOLO首先将图片划分成SxS个区域，注意这个区域的概念不同于上文提及将图片划分成N个区域扔进detector这里的区域不同。上文提及的区域是真的将图片进行剪裁，或者说把图片的某个局部的像素扔进detector，而这里的划分区域，只的是逻辑上的划分。

40.梯度消失梯度爆炸怎么解决

1）、使用 ReLU、LReLU、ELU、maxout 等激活函数

sigmoid函数的梯度随着x的增大或减小和消失，而ReLU不会。

2）、使用批规范化

通过规范化操作将输出信号x规范化到均值为0，方差为1保证网络的稳定性。从上述分析分可以看到，反向传播式子中有w的存在，所以w的大小影响了梯度的消失和爆炸，Batch Normalization 就是通过对每一层的输出规范为均值和方差一致的方法，消除了w带来的放大缩小的影响，进而解决梯度消失和爆炸的问题。

41. RNN容易梯度消失，怎么解决？

1）、梯度裁剪（Clipping Gradient）

既然在BP过程中会产生梯度消失（就是偏导无限接近0，导致长时记忆无法更新），那么最简单粗暴的方法，设定阈值，当梯度小于阈值时，更新的梯度为阈值。

优点：简单粗暴

缺点：很难找到满意的阈值

2）、LSTM（Long Short-Term Memory）

一定程度上模仿了长时记忆，相比于梯度裁剪，最大的优点就是，自动学习在什么时候可以将error反向传播，自动控制哪些是需要作为记忆存储在LSTM cell中。一般长时记忆模型包括写入，读取，和忘记三个过程对应到LSTM中就变成了input_gate,output_gate,

forget_gate,三个门，范围在0到1之间，相当于对输入输出进行加权的学习，利用大量数据来自动学习加权的参数（即学习了哪些错误可以用BP更新参数）。具体的公式表达：

优点：模型自动学习更新参数

42. LSTM跟RNN有啥区别

LSTM与RNN的比较

RNN在处理long term memory的时候存在缺陷，因此LSTM应运而生。LSTM是一种变种的RNN，它的精髓在于引入了细胞状态这样一个概念，不同于RNN只考虑最近的状态，LSTM的细胞状态会决定哪些状态应该被留下来，哪些状态应该被遗忘。

下面来看一些RNN和LSTM内部结构的不同：

RNN

LSTM

由上面两幅图可以观察到，LSTM结构更为复杂，在RNN中，将过去的输出和当前的输入concatenate到一起，通过tanh来控制两者的输出，它只考虑最近时刻的状态。在RNN中有两个输入和一个输出。

而LSTM为了能记住长期的状态，在RNN的基础上增加了一路输入和一路输出，增加的这一路就是细胞状态，也就是途中最上面的一条通路。事实上整个LSTM分成了三个部分：

1）哪些细胞状态应该被遗忘

2）哪些新的状态应该被加入

3）根据当前的状态和现在的输入，输出应该是什么

下面来分别讨论：

1）哪些细胞状态应该被遗忘

这部分功能是通过sigmoid函数实现的，也就是最左边的通路。根据输入和上一时刻的输出来决定当前细胞状态是否有需要被遗忘的内容。举个例子，如果之前细胞状态中有主语，而输入中又有了主语，那么原来存在的主语就应该被遗忘。concatenate的输入和上一时刻的输出经过sigmoid函数后，越接近于0被遗忘的越多，越接近于1被遗忘的越少。

2）哪些新的状态应该被加入

继续上面的例子，新进来的主语自然就是应该被加入到细胞状态的内容，同理也是靠sigmoid函数来决定应该记住哪些内容。但是值得一提的是，需要被记住的内容并不是直接

concatenate的输入和上一时刻的输出，还要经过tanh，这点应该也是和RNN保持一致。并且需要注意，此处的sigmoid和前一步的sigmoid层的w和b不同，是分别训练的层。

细胞状态在忘记了该忘记的，记住了该记住的之后，就可以作为下一时刻的细胞状态输入了。

3）根据当前的状态和现在的输入，输出应该是什么

这是最右侧的通路，也是通过sigmoid函数做门，对第二步求得的状态做tanh后的结果过滤，从而得到最终的预测结果。

事实上，LSTM就是在RNN的基础上，增加了对过去状态的过滤，从而可以选择哪些状态对当前更有影响，而不是简单的选择最近的状态。

在这之后，研究人员们实现了各种LSTM的变种网络。不变的是，通常都会用sigmoid函数做门，筛选状态或者输入。并且输出都是要经过tanh函数。具体为什么要用这两个函数，由于刚接触还不能给出一定的解释，日后理解了再补充。

43.卷积层和池化层有什么区别？

44. dropout咋回事讲讲

Dropout的目标是在指数级数量的神经网络上近似这个过程。Dropout训练与Bagging训练不太一样。在Bagging的情况下,所有模型是独立的。

在Dropout的情况下,模型是共享参数的,其中每个模型继承的父神经网络参数的不同子集。参数共享使得在有限可用的内存下代表指数数量的模型变得可能。在Bagging的情况下,每一个模型在其相应训练集上训练到收敛。

在Dropout的情况下,通常大部分模型都没有显式地被训练,通常该模型很大,以致到宇宙毁灭都不能采样所有可能的子网络。取而代之的是,可能的子网络的一小部分训练单个步骤,参数共享导致剩余的子网络能有好的参数设定。

45.relu：

在深度神经网络中，通常使用一种叫修正线性单元(Rectified linear unit，ReLU）作为神经元的激活函数。ReLU起源于神经科学的研究：2001年，Dayan、Abott从生物学角度模拟出了脑神经元接受信号更精确的激活模型，如下图：

其中横轴是时间(ms)，纵轴是神经元的放电速率(Firing Rate)。同年，Attwell等神经科学家通过研究大脑的能量消耗过程，推测神经元的工作方式具有稀疏性和分布性；2003年Lennie等神经科学家估测大脑同时被激活的神经元只有1~4%，这进一步表明了神经元的工作稀疏性。而对于ReLU函数而言，类似表现是如何体现的？其相比于其他线性函数(如purlin)和非线性函数(如sigmoid、双曲正切)又有何优势？下面请各位看官容我慢慢道来。

首先，我们来看一下ReLU激活函数的形式，如下图：

从上图不难看出，ReLU函数其实是分段线性函数，把所有的负值都变为0，而正值不变，这种操作被成为单侧抑制。可别小看这个简单的操作，正因为有了这单侧抑制，才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中，当模型增加N层之后，理论上ReLU神经元的激活率将降低2的N次方倍。这里或许有童鞋会问：ReLU的函数图像为什么一定要长这样？反过来，或者朝下延伸行不行？其实还不一定要长这样。只要能起到单侧抑制的作用，无论是镜面翻转还是180度翻转，最终神经元的输出也只是相当于加上了一个常数项系数，并不影响模型的训练结果。之所以这样定，或许是为了契合生物学角度，便于我们理解吧。

那么问题来了：这种稀疏性有何作用？换句话说，我们为什么需要让神经元稀疏？不妨举栗子来说明。当看名侦探柯南的时候，我们可以根据故事情节进行思考和推理，这时用到的是我们的大脑左半球；而当看蒙面唱将时，我们可以跟着歌手一起哼唱，这时用到的则是我们的右半球。左半球侧重理性思维，而右半球侧重感性思维。也就是说，当我们在进行运算或者欣赏时，都会有一部分神经元处于激活或是抑制状态，可以说是各司其职。再比如，生病了去医院看病，检查报告里面上百项指标，但跟病情相关的通常只有那么几个。与之类似，当训练一个深度分类模型的时候，和目标相关的特征往往也就那么几个，因此通过ReLU实现稀疏后的模型能够更好地挖掘相关特征，拟合训练数据。

此外，相比于其它激活函数来说，ReLU有以下优势：对于线性函数而言，ReLU的表达能力更强，尤其体现在深度网络中；而对于非线性函数而言，ReLU由于非负区间的梯度为常数，因此不存在梯度消失问题(Vanishing Gradient Problem)，使得模型的收敛速度维持在一个稳定状态。这里稍微描述一下什么是梯度消失问题：当梯度小于1时，预测值与真实值之间的误差每传播一层会衰减一次，如果在深层模型中使用sigmoid作为激活函数，这种现象尤为明显，将导致模型收敛停滞不前。

46.神经网络为啥用交叉熵？

通过神经网络解决多分类问题时，最常用的一种方式就是在最后一层设置n个输出节点，无论在浅层神经网络还是在CNN中都是如此，比如，在AlexNet中最后的输出层有1000个节点，而即便是ResNet取消了全连接层，也会在最后有一个1000个节点的输出层。

一般情况下，最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N，那么对于每一个样例，神经网络可以得到一个N维的数组作为输出结果，数组中每一个维度会对应一个类别。在最理想的情况下，如果一个样本属于k，那么这个类别所对应的的输出节点的输出值应该为1，而其他节点的输出都为0，即[0,0,1,0,….0,0]，这个数组也就是样本的Label，是神经网络最期望的输出结果，交叉熵就是用来判定实际的输出与期望的输出的接近程度。

47.注意力公式

Soft attention、global attention、动态attention

Hard attention

静态attention“半软半硬”的attention （local attention）

强制前向attention

48.Flappy.Bird开发者,怎么利用DNQ方法强化学习你的游戏AI

强化学习是机器学习里面的一个分支。它强调如何基于环境而行动，以取得最大化的预期收益。其灵感来源于心理学中的行为主义理论，既有机体如何在环境给予的奖励或者惩罚的刺激下，逐步形成对刺激的预期，产生能够最大利益的习惯性行为。结构简图如下：

因为强化学习考虑到了自主个体、环境、奖励等因素，所以很多人包括强化学习的研究者Richard Sutton 都认为它是人工智能中最高层的模型，其它深度学习、机器学习模型都是它的子系统。在围棋界先后打败世界冠军的李世乭和柯洁额alphaGo就使用了强化学习模型，也正是这两次比赛，把人工智能这个概念传递给了大众。使用的是卷积神经网络结构。

49.LeNet-5结构

输入层：32∗3232∗32的图片，也就是相当于10241024个神经元

C1层:选取66个特征卷积核，大小为5∗55∗5(不包含偏置),得到66个特征图，每个特征图的大小为32−5+1=2832−5+1=28，也就是神经元的个数由10241024减小到了28∗28=78428∗28=784。

输入层与C1层之间的参数:6∗(5∗5+1)6∗(5∗5+1),对于卷积层C1，每个像素都与前一层的5∗55∗5个像素和11个bias有连接，有6∗(5∗5+1)∗(28∗28)6∗(5∗5+1)∗(28∗28)个连接

S2层:池化,是一个下采样层（为什么是下采样？利用图像局部相关性的原理，对图像进行子抽样，可以减少数据处理量同时保留有用信息），有66个14∗1414∗14的特征图，特征图中的每个单元与C1中相对应特征图的2∗22∗2邻域相连接。S2S2层每个单元对应C1C1中44个求和，乘以一个可训练参数，再加上一个可训练偏置。

C1与S2之间的参数:每一个2∗22∗2求和，然后乘以一个参数，加上一个偏置，共计2∗6=122∗6=12个参数。S2S2中的每个像素都与C1C1中的2∗22∗2个像素和11个偏置相连接，所以有6∗5∗14∗14=58806∗5∗14∗14=5880个连接

C3层:选取卷积核大小为5∗55∗5,得到新的图片大小为10∗1010∗10我们知道S2包含：6张14∗146张14∗14大小的图片，我们希望这一层得到的结果是：16张10∗1016张10∗10的图片。这1616张图片的每一张，是通过S2S2的66张图片进行加权组合得到的，具体是怎么组合的呢？

S2与C3之间的组合

前66个feature map与S2S2层相连的33个feature map相连接，后面66个feature map与S2层相连的4个S2层相连的4个feature map相连接，后面33个feature map与S2S2层部分不相连的44个feature map相连接，最后一个与S2S2层的所有feature map相连。卷积核大小依然为5∗55∗5，总共有6∗（3∗5∗5+1）6∗（3∗5∗5+1）+6∗（4∗5∗5+1）6∗（4∗5∗5+1）+3∗（4∗5∗5+1）3∗（4∗5∗5+1）+1∗（6∗5∗5+1）=15161∗（6∗5∗5+1）=1516个参数。而图像大小为10∗1010∗10，所以共有151600151600个连接。

S4层

池化，窗口大小为2∗22∗2,有1616个特征图，总共有3232个参数

C3与S4之间的参数

16∗（25∗4+25）=200016∗（25∗4+25）=2000个连接

C5层

总共120120个feature map，每个feature map与S4S4层所有的feature map相连接，卷积核大小是5∗55∗5，而S4S4层的feature map的大小也是5∗55∗5，所以C5C5的feature map就变成了1个点，共计有120（25∗16+1）=48120120（25∗16+1）=48120个参数。

F6层

全连接

F6F6相当于MLP中的隐含层，有8484个节点，所以有84∗（120+1）=1016484∗（120+1）=10164个参数。F6F6层采用了正切函数。

输出层

采用了RBF函数，即径向欧式距离函数。

50.推导LSTM正向传播和反向传播过程：

前向推导过程：

反向推导过程：

51.LSTM原理，与GRU区别：

LSTM算法全称为Long short-term memory，是一种特定形式的RNN（Recurrent neural network，循环神经网络），而RNN是一系列能够处理序列数据的神经网络的总称。

RNN在处理长期依赖（时间序列上距离较远的节点）时会遇到巨大的困难，因为计算距离较远的节点之间的联系时会涉及雅可比矩阵的多次相乘，这会带来梯度消失（经常发生）或者梯度膨胀（较少发生）的问题，这样的现象被许多学者观察到并独立研究。为了解决该问题，研究人员提出LSTM。

LSTM是门限RNN，其单一节点的结构如下图1所示。LSTM的巧妙之处在于通过增加输入门限，遗忘门限和输出门限，使得自循环的权重是变化的，这样一来在模型参数固定的情况下，不同时刻的积分尺度可以动态改变，从而避免了梯度消失或者梯度膨胀的问题。

图1 LSTM的CELL示意图

根据LSTM网络的结构，每个LSTM单元的计算公式如下图2所示，其中Ft表示遗忘门限，It表示输入门限，Ct表示前一时刻cell状态、Ct表示cell状态（这里就是循环发生的地方），Ot表示输出门限，Ht表示当前单元的输出，Ht-1表示前一时刻单元的输出。

图2 LSTM计算公式

与GRU区别：1）GRU和LSTM的性能在很多任务上不分伯仲。2）GRU 参数更少因此更容易收敛，但是数据集很大的情况下，LSTM表达性能更好。3）从结构上来说，GRU只有两个门（update和reset），LSTM有三个门（forget，input，output），GRU直接将hidden state 传给下一个单元，而LSTM则用memory cell 把hidden state 包装起来。

52. DNN的梯度更新方式

1）批量梯度下降法BGD

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，其数学形式如下：

(1) 对上述的能量函数求偏导：

(2) 由于是最小化风险函数，所以按照每个参数的梯度负方向来更新每个：

2）随机梯度下降法SGD

由于批量梯度下降法在更新每一个参数时，都需要所有的训练样本，所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法（Stochastic Gradient Descent，简称SGD）正是为了解决批量梯度下降法这一弊端而提出的。

将上面的能量函数写为如下形式：

利用每个样本的损失函数对求偏导得到对应的梯度，来更新：

3）小批量梯度下降法MBGD

有上述的两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。

53.CNN为什么比DNN在图像识别上更好

DNN的输入是向量形式，并未考虑到平面的结构信息，在图像和NLP领域这一结构信息尤为重要，例如识别图像中的数字，同一数字与所在位置无关（换句话说任一位置的权重都应相同）。

CNN的输入可以是tensor，例如二维矩阵，通过filter获得局部特征，较好的保留了平面结构信息。

54.Inception Score 评价指标介绍

定义：

推导出上式的意义：

故要使得生成图像的inception score高，就需要

1.最大化H(y);也就是对于输入的样本，通过inception_v3模型后的类别要均衡，衡量模式坍塌。

2.最小化H(y|x);说明对于输入的样本，通过inception_v3模型后预测某类别的置信度要高，衡量图片生成的质量。

55.使用的 CNN 模型权重之间有关联吗？

权重之间有关联。CNN是权重共享，减少了参数的数量。

简单来说就是用一个卷积核来和一个图像来进行卷积，记住是同一个卷积核，不改变卷积核的值。这样可以减少权值参数。共享就是一个图片对卷积核是共同享有的。对于一个100*100像素的图像，如果我们用一个神经元来对图像进行操作，这个神经元大小就是100*100=10000，单如果我们使用10*10的卷积核，我们虽然需要计算多次，但我们需要的参数只有10*10=100个，加上一个偏向b，一共只需要101个参数。我们取得图像大小还是100*100。如果我们取得图像比较大，它的参数将会更加多。我们通过10*10的卷积核对图像进行特征提取，这样我们就得到一个Feature Map。

一个卷积核只能提取一个特征，所以我们需要多几个卷积核，假设我们有6个卷积核，我们就会得到6个Feature Map，将这6个Feature Map组成一起就是一个神经元。这6个Feature Map我们需要101*6=606个参数。这个值和10000比还是比较小的。如果像之前的神经网络, 两两相连, 需要 28x28 = 784 输入层, 加上第一个隐藏层30个神经元, 则需要784x30再加上30个b, 总共23,550个参数! 多了40倍的参数。

5、百度实习：1）模型压缩方法；2）CPM 模型压缩用了哪些方法；3）压缩效果（体积、指标、部署）；4）Kaggle 比赛，比赛背景，怎么进行数据清洗，类别平衡，相近类别重分类，最终成绩是多少，觉得跟前几名差距在哪，有没有尝试过集成的方法；5）人脸项目，大概流程，GPU 加速的地方，两个网络的训练过程，级联网络的 inference 过程，能同时检测多个人脸吗？多尺度缩放怎么处理，resize 自己写？只是检测吗，有没有识别？或者其他

56.CycleGAN 原理介绍一下

CycleGAN其实就是一个A→B单向GAN加上一个B→A单向GAN。两个GAN共享两个生成器，然后各自带一个判别器，所以加起来总共有两个判别器和两个生成器。一个单向GAN有两个loss，而CycleGAN加起来总共有四个loss。CycleGAN论文的原版原理图和公式如下，其实理解了单向GAN那么CycleGAN已经很好理解。

下面放一张网友们自制的CycleGAN示意图，比论文原版的更加直观，出处见水印。

57. 训练 GAN 的时候有没有遇到什么问题?

遇到GAN训练不稳定问题。通过Wasserstein GAN来解决这个问题。WGAN前作分析了Ian Goodfellow提出的原始GAN两种形式各自的问题，第一种形式等价在最优判别器下等价于最小化生成分布与真实分布之间的JS散度，由于随机生成分布很难与真实分布有不可忽略的重叠以及JS散度的突变特性，使得生成器面临梯度消失的问题；第二种形式在最优判别器下等价于既要最小化生成分布与真实分布直接的KL散度，又要最大化其JS散度，相互矛盾，导致梯度不稳定，而且KL散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性，导致collapse mode现象。

WGAN前作针对分布重叠问题提出了一个过渡解决方案，通过对生成样本和真实样本加噪声使得两个分布产生重叠，理论上可以解决训练不稳定的问题，可以放心训练判别器到接近最优，但是未能提供一个指示训练进程的可靠指标，也未做实验验证。

WGAN本作引入了Wasserstein距离，由于它相对KL散度与JS散度具有优越的平滑特性，理论上可以解决梯度消失问题。接着通过数学变换将Wasserstein距离写成可求解的形式，利用一个参数数值范围受限的判别器神经网络来最大化这个形式，就可以近似Wasserstein距离。在此近似最优判别器下优化生成器使得Wasserstein距离缩小，就能有效拉近生成分布与真实分布。WGAN既解决了训练不稳定的问题，也提供了一个可靠的训练进程指标，而且该指标确实与生成样本的质量高度相关。

58.CPM 模型压缩怎么做的？有压过 OpenPose 吗？

预测和图像特征计算模块可以被深度网络架构来取代，其中图像和组织特征的表达可以从数据中直接学习。卷积架构让全局可导，因此可以CPM所有阶段联合训练。CPM可以描述为在PM隐含空间模型框架下的卷积架构。

1）用局部图线索来进行关键定位

第一阶段只用局部图线索来预测部件信任度。figure 2c展示用本地图信息的部件检测的深度网络。先序哦是局部的因为第一阶段感知野只是输出像素附近的一小块。我们用5层卷机网络组成的结构（尾部是量个1x`1卷积层的全卷积架构）。实践中，为了得到一定精度，我们把图片标准化为368x368，感受野是160x160.网络可以看成让深度网络在图像上滑动，并将160x160中局部图像线索回归至代表了各个部件在各个位置的score的P+1大小输出向量。

2）基于空间环境信息的级联预测

对于性状稳定的头和肩膀，检测效果很好，然而人体骨架的连接处准确率就很低，因为形状差异很大。部件周围的信任映射，虽然有噪声，但是很有价值。figure 3中，当检测右手肘时，右肩膀的信任映射达到高峰，可以成为一个很强的线索。后续阶段的预测器（gt）可以用图位置z附近含有噪声的信任映射里的空间组织信息（fai），并且利用“部件的几何设定都是恒定的”这一事实来提高改善预测。

第二个阶段，分类器g2接收特征x2和前一阶段fai的输入。前一阶段不同部件的位置z附近的空间区域产生信任映射，特征方程是把信任映射出的特点编码。CPM不用显式方程来计算环境特征，而是定义含有前一阶段信任度的fai作为预测机的感受野。

这个网络的设计为了在第二阶段输出层得到一个足够大的感知野，可以学习复杂和长距离的部件关系。通过应用迁移阶段的输出层特征（而不是用图模型的显式方程），后续卷积层自由结合最有预测力的特征，来形成环境信息。第一阶段的信任映射来自用小感知野来检验局部图像的网络。第二阶段，我们设计了一个极大扩充的等价感知野。大感知野可以用两种方法实现：牺牲准确度的池化，增加参数为代价的加大卷积核大小，或者冒着可能让反传消失风险增加网络层数。我们选择增加卷积层，在8x降维热力图上达到大感知野，让我们尽可能减少参数数量。8步网络更容易获得大感知野，它和4步网络表现一样好（在高精确度区域也是）。我们也在PM之后图像特征上映射上重复了类似架构，让空间组织依赖图像而且允许错误关联。

我们发现，感受野变大，准确性也变大。通过一系列实验，figure 4的准确度随着感受野的变化曲线，改变感受野只通过改变结构而不是增加参数。准确度随着感受野变大而变大，在250像素饱和，这也大概是归一化物体的大小。这说明，网络确实让远距离物体关系编码，并且这是有益的。我们最好的数据集中，我们把图像归一化为368x368，基于第一级信任映射的第二级感知野输出是31x31,这和原始图片的400x400像素等价，其半径可以覆盖任何部件。当阶段增多，有效感知野就会变大。我们有6个阶段。

3）用CPM学习

这个深度架构可以有许多层。训练这个网可能让梯度消失，就是反向传播在中间层会减弱。pm级联预测框架有一个自然的解决这个问题的方法。我们不断激励这个网络，通过在每个阶段t的输出定义一个损失函数，让预测的和实际信任映射的距离最小化。部件p理想的信任映射是bp，通过把p部件的最可能点设定在ground truth位置。

压缩过OpenPose，效果还可以。

59.用过哪些 Optimizer，效果如何?

1）SGD；2）Momentum；3）Nesterov；4）Adagrad；5）Adadelta；6）RMSprop；7）Adam；8）Adamax；9）Nadam。（1）对于稀疏数据，尽量使用学习率可自适应的算法，不用手动调节，而且最好采用默认参数。（2）SGD通常训练时间最长，但是在好的初始化和学习率调度方案下，结果往往更可靠。但SGD容易困在鞍点，这个缺点也不能忽略。（3）如果在意收敛的速度，并且需要训练比较深比较复杂的网络时，推荐使用学习率自适应的优化方法。（4）Adagrad，Adadelta和RMSprop是比较相近的算法，表现都差不多。（5）在能使用带动量的RMSprop或者Adam的地方，使用Nadam往往能取得更好的效果。

60.图像基础：传统图像处理方法知道哪些，图像对比度增强说一下?

数字图像处理常用方法：

1）图像变换：由于图像阵列很大，直接在空间域中进行处理，涉及计算量很大。因此，往往采用各种图像变换的方法，如傅立叶变换、沃尔什变换、离散余弦变换等间接处理技术，将空间域的处理转换为变换域处理，不仅可减少计算量，而且可获得更有效的处理（如傅立叶变换可在频域中进行数字滤波处理）。目前新兴研究的小波变换在时域和频域中都具有良好的局部化特性，它在图像处理中也有着广泛而有效的应用。

2）图像编码压缩：图像编码压缩技术可减少描述图像的数据量（即比特数），以便节省图像传输、处理时间和减少所占用的存储器容量。压缩可以在不失真的前提下获得，也可以在允许的失真条件下进行。编码是压缩技术中最重要的方法，它在图像处理技术中是发展最早且比较成熟的技术。

3）图像增强和复原：图像增强和复原的目的是为了提高图像的质量，如去除噪声，提高图像的清晰度等。图像增强不考虑图像降质的原因，突出图像中所感兴趣的部分。如强化图像高频分量，可使图像中物体轮廓清晰，细节明显；如强化低频分量可减少图像中噪声影响。图像复原要求对图像降质的原因有一定的了解，一般讲应根据降质过程建立“降质模型”，再采用某种滤波方法，恢复或重建原来的图像。

4）图像分割：图像分割是数字图像处理中的关键技术之一。图像分割是将图像中有意义的特征部分提取出来，其有意义的特征有图像中的边缘、区域等，这是进一步进行图像识别、分析和理解的基础。虽然目前已研究出不少边缘提取、区域分割的方法，但还没有一种普遍适用于各种图像的有效方法。因此，对图像分割的研究还在不断深入之中，是目前图像处理中研究的热点之一。

5）图像描述：图像描述是图像识别和理解的必要前提。作为最简单的二值图像可采用其几何特性描述物体的特性，一般图像的描述方法采用二维形状描述，它有边界描述和区域描述两类方法。对于特殊的纹理图像可采用二维纹理特征描述。随着图像处理研究的深入发展，已经开始进行三维物体描述的研究，提出了体积描述、表面描述、广义圆柱体描述等方法。

6）图像分类（识别）：图像分类（识别）属于模式识别的范畴，其主要内容是图像经过某些预处理（增强、复原、压缩）后，进行图像分割和特征提取，从而进行判决分类。图像分类常采用经典的模式识别方法，有统计模式分类和句法（结构）模式分类，近年来新发展起来的模糊模式识别和人工神经网络模式分类在图像识别中也越来越受到重视。

全局对比度增强

1. 直方图均衡化 Histogram Equalization

算法：

1）根据图像灰度计算灰度概率密度函数PDF

2）计算累积概率分布函数CDF

3）将CDF归一化到原图灰度取值范围，如[0,255]。

4）之后CDF四舍五入取整，得到灰度转换函数sk=T(rk)

5）将CDF作为转换函数，将灰度为rk的点转换为sk灰度

2. 直方图匹配 Histogram Matching

算法：

1）根据图像计算概率密度分布pr(r)；

2）根据pr(r)计算累计分布函数sk=T(rk)；

3）根据给定的目标分布pz(z)计算累计分布函数G(zq)；

4）对于每一个k，找到一个q，使得G(zq)约等于sk；

5）将原图中灰度为k的点变为灰度q；

局部对比度增强

1. 邻域直方图均衡：将全局直方图均衡的思想应用于邻域直方图处理中。

2. 邻域直方图匹配：将全局直方图匹配的思想应用于邻域直方图处理中。

3. 邻域统计方法

算法

1）初始化：增强常数E，灰度下阈值k0，标准差下阈值k1，标准差上阈值k2，窗口半宽s；

2）计算图像灰度均值MG和灰度标准差σG；

3）对于每一个像素，计算邻域（大小为2∗step+1的方块）内灰度均值ML和标准差σL；

4）如果ML<=k0∗MGML<=k0∗MG并且k1∗σG<=σL<=k2∗σG，将像素灰度乘以E。

61.介绍一下图像的高频、低频部分，知道哪些图像补全的方法?

图像的频率：灰度值变化剧烈程度的指标，是灰度在平面空间上的梯度。

（1）什么是低频?

低频就是颜色缓慢地变化,也就是灰度缓慢地变化,就代表着那是连续渐变的一块区域,这部分就是低频. 对于一幅图像来说，除去高频的就是低频了，也就是边缘以内的内容为低频，而边缘内的内容就是图像的大部分信息，即图像的大致概貌和轮廓，是图像的近似信息。

（2）什么是高频?

反过来, 高频就是频率变化快.图像中什么时候灰度变化快?就是相邻区域之间灰度相差很大,这就是变化得快.图像中,一个影像与背景的边缘部位,通常会有明显的差别,也就是说变化那条边线那里,灰度变化很快,也即是变化频率高的部位.因此，图像边缘的灰度值变化快，就对应着频率高，即高频显示图像边缘。图像的细节处也是属于灰度值急剧变化的区域，正是因为灰度值的急剧变化，才会出现细节。

另外噪声（即噪点）也是这样,在一个像素所在的位置,之所以是噪点,就是因为它与正常的点颜色不一样了，也就是说该像素点灰度值明显不一样了,,也就是灰度有快速地变化了,所以是高频部分，因此有噪声在高频这么一说。

图像补全的方法：

Region Filling and Object Removal by Exemplar-Based Image Inpainting

算法的流程大致如下：

1）对待补全区域边界的像素依次计算补全的优先度(priority)，这个优先度主要考虑2个因素。一个是周围像素可信度高的位置要优先补，另一个是位于图像梯度变化剧烈的位置要优先补。综合二者得到所有优先度之后，挑选优先度最高的像素来补

2）对于上一步找到的待补全像素，考虑它周围的一个小patch(比如3*3)。在图像已知部分搜索所有的patch，找到最相似的patch

3）用找到的best match来补全未知部分，并更新相关数值

但是我们也不难发现这个方法存在的问题：如果图像已知部分找不到相似的patch，那算法将无法进行；这个方法只适用于补全背景以低频信息和重复性纹理为主的图像；搜索相似的patch计算复杂度非常高，算法运行效率低。

Scene Completion Using Millions of Photographs

算法的大致流程如下：

1）从Flickr上下载两百万图片构建数据库，以”landscape””city””park”等关键词搜索户外场景的图片。

2）对于一张待补全图像，从数据库中挑选200个场景最相似的图片，这里使用gist scene descriptor和图像下采样到4*4作为匹配的特征向量。

3）将补全区域边界外80个pixel的区域作为context。对于每一张匹配的图像，搜索所有的平移空间和3个尺度的scale空间，根据context部分的匹配误差，选择最佳的补全位置；之后利用graph-cut算法求解最佳的融合边界。

4）利用标准的泊松融合处理融合边界。

5）将前几步的匹配cost和graph-cut的cost加起来，返回cost最小的20的结果供用户挑选。

Context Encoders: Feature Learning by Inpainting

文章提出的网络结构如下，包括3个部分：Encoder, Channel-wise fully-connected layer, Decoder。Encoder的结构直接借鉴了AlexNet前5层的卷积层结构，具体结构如下。输入的crop尺寸是227Í227，卷积之后得到的feature map结构是256层6 Í 6。所有的weight都随机初始化。

Channel-wise fully-connected layer是对普通fc层的一种改进。之所以加入fc层是为了使feature map每一层的信息可以在内部交流。但传统的fc层参数太多，因此作者提出可以在fc中去掉feature map层间的信息交流，从而减少参数规模。在fc之后会接一个stride为1的卷积层，来实现层间的信息交流。

Decoder的目的是将压缩的feature map一步步放大，恢复到原始图片的尺寸。文章提出采用5个up-convolutional层，每层后接一个RELU。上采样的结构如下。

62.百度实习：模型压缩的大方向。CPM 模型怎么压缩的，做了哪些工作？

1）用局部图线索来进行关键定位

2）基于空间环境信息的级联预测

3）用CPM学习

63.Depthwise 卷积实际速度与理论速度差距较大，解释原因。

首先，caffe原先的gpu实现group convolution很糟糕，用for循环每次算一个卷积，速度极慢。第二，cudnn7.0及之后直接支持group convolution，但本人实测，速度比github上几个直接写cuda kernel计算的dw convolution速度慢。例如对于n=128, c=512, h=32, w=32, group=512的卷积跑100次，cudnn 7.0里的group convolution需要4秒多，而DepthwiseConvolution大概只需要1秒。

分析了一下dw convolution与普通convolution的理论计算复杂度，举例如下：

卷积1：普通卷积，输入为64*64*256，输出为64*64*256，卷积核大小为3*3。参数为3*3*256*256=590K，计算量为64*64*256*3*3*256=2.42G，计算过程的工作集内存总量（输入输出数据+参数）为64*64*256*2 + 3*3*256*256 = 2.69M。

卷积2：dw卷积，输入为64*64*256，输出为64*64*256，卷积核大小为3*3。参数为3*3*256=2.3K个，计算量为64*64*256*3*3=9.44M，计算过程的工作集内存总量为64*64*256*2 + 3*3*256=2.10M。

卷积3：普通卷积，输入为64*64*16，输出为64*64*16，卷积核大小为3*3。参数为3*3*16*16=2.3K个，计算量为64*64*16*3*3*16=9.44M，计算过程的工作集内存总量为64*64*16*2 + 3*3*16*16=133K。

可以看到卷积2肯定比卷积1快，因为计算量下降到1/256了，但卷积2实际上无法达到卷积1的256倍速度（我记得我测得结果大概是快10倍左右），因为工作集内存大小并没有显著降低。卷积2也无法达到卷积3的速度，因为虽然FLOPS相同，但工作集内存大小相差了很多倍，因此单位数据的计算密度小很多，很难充分利用GPU上的计算单元。

64.RetinaNet 的大致结构画一下

65.RetinaNet为什么比SSD效果好?

SSD 在训练期间重新采样目标类和背景类的比率，这样它就不会被图像背景淹没。RetinaNet采用另一种方法来减少训练良好的类的损失。因此，只要该模型能够很好地检测背景，就可以减少其损失并重新增强对目标类的训练。所以RetinaNet比SSD 效果好。

三、数学基础知识（10%）

1. 一个活动,n个女生手里拿着长短不一的玫瑰花,无序的排成一排,一个男生从头走到尾,试图拿更长的玫瑰花,一旦拿了一朵就不能再拿其他的,错过了就不能回头。问男生最好的策略?

策略：不选取前r-1个女生,只从剩下的n-r+1个女生开始选取,若这个女生比之前任何一个女生玫瑰花都长则选取这个女生。

预计求爱者有 n 个人，你应该先拒绝掉前 n/e 个人，静候下一个比这些人都好的人。假设你一共会遇到大概 30 个求爱者，就应该拒绝掉前 30/e ≈ 30/2.718 ≈ 11 个求爱者，然后从第 12 个求爱者开始，一旦发现比前面 11 个求爱者都好的人，就果断接受他。由于 1/e 大约等于 37%，因此这条爱情大法也叫做 37% 法则。

条件概率：

$P(A|B)=\frac{P(AB)}{P(B)}$

贝叶斯公式：

推导：

策略：不选取前r-1个女生，从第r个女生开始选，碰到比前面女生都长的就确定选择。

假设从第r个女生开始选,则男生能够选到最长玫瑰花的概率为:

P关于r有极大值， $r=\frac{n}{e}=0.37n$ 时，P有极大值37%。

2.某大公司有这么一个规定：只要有一个员工过生日，当天所有员工全部放假一天；但在其余时候，所有员工都没有假期，必须正常上班。这个公司需要雇用多少员工，才能让公司一年内所有员工的总工作时间期望值最大？

假设一年有365 天，每个员工的生日都概率均等地分布在这 365 天里。

总工作时间期望 $E=n*(1-\frac{1}{365})^{n}$ ，单位：年。

n=365时，E有极大值134

3.切比雪夫不等式

4.一根绳子,随机截成3段,可以组成一个三角形的概率有多大

设绳子长为a,折成三段的长度为x,y,a-x-y从而得到,满足这三个约束条件在平面直角坐标系中的可行域为一个直角三角形,面积为。

而构成三角形的条件,任意两边和大于第三边的条件x+y>a-x-y,a-y>y,a-x>x同时成立。满足以上不等式在平面直角坐标系中也是一个直角三角形,面积为。

所以构成三角形概率为

5.概率题：抽蓝球红球，蓝结束红放回继续，平均结束游戏抽取次数

根据红球和蓝球的个数，依据概率公式，求出平均抽取次数。

6.最大似然估计（MLE）和最大后验概率估计（MAP）的区别?

最大似然估计

最大似然估计是求 θ, 使似然函数 P(x0∣θ)最大，求得似然函数偏导为0的θ。

最大后验概率估计

最大后验概率估计则是求θ，使P(x0∣θ)P(θ)最大；相比最大似然估计，引入了一个先验分布P(θ)。

7.频率学派和贝叶斯学派的区别

（1）频率派认为抽样是无限的,在无限的抽样中,对于决策的规则可以很精确。贝叶斯派认为世界无时无刻不在改变,未知的变量和事件都有一定的概率,即后验概率是先验概率的修正。

（2）频率派认为模型参数是固定的,一个模型在无数次抽样后,参数是不变的。而贝叶斯学派认为数据才是固定的而参数并不是。

（3）频率派认为模型不存在先验而贝叶斯派认为模型存在先验。

8.什么是共轭先验分布

假设为总体分布中的参数,的先验密度函数为,而抽样信息算得的后验密度函数与具有相同的函数形式,则称为的共轭先验分布。（先验、后验具有相同的函数形式，则这个函数为参数的共轭先验分布）

9. 概率和似然的区别

概率是指在给定参数的情况下,样本的随机向量X=x0的可能性。（针对变量）

似然表示的是在给定样本X=x0的情况下,参数为真实值的可能性。一般情况,对随机变量的取值用概率表示。而在非贝叶斯统计的情况下,参数为一个实数而不是随机变量,一般用似然来表示。（针对参数）

10. 0~1均匀分布的随机器如何变化成均值为0，方差为1的随机器

0~1的均匀分布是均值为1/2，方差为1/12.转成均值为0，方差为1。

密度函数：f(x)

分布函数：F(x0)=P（x<=x0）

密度函数和分布函数的关系：

期望：

方差：

用 Box-Muller 变换，或者变量减去1/2，然后乘以根号12.

11、求A（mk）和B（nk）向量集的欧几里得距离？（矩阵之间欧氏距离：A，B矩阵各个向量两两之间的欧式距离）（A、B均为向量集形成的矩阵）

以下为用矩阵运算实现：

先得到矩阵（m*n）,然后对矩阵A和矩阵分别求出其中每个向量的模平方,并扩展为两个m*k的矩阵和（长宽与A一致）。最终求得新的矩阵,并将此矩阵开平方得到A,B向量集的欧几里得距离。

欧几里得距离，是最常见的距离度量，衡量的是多维空间中两个向量（或更高维的）之间的绝对距离。

11.机器学习中的距离计算方法?

（1）欧式距离:

（2）曼哈顿距离:

（3）余弦距离:

（4）切比雪夫距离

12、欧拉公式：

13、编辑距离

概念：

编辑距离的作用主要是用来比较两个字符串的相似度的。

编辑距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

在概念中，我们可以看出一些重点那就是，编辑操作只有三种。插入，删除，替换这三种操作，我们有两个字符串，将其中一个字符串经过上面的这三种操作之后，得到两个完全相同的字符串付出的代价是什么就是我们要讨论和计算的。

算法过程：

1.str1或str2的长度为0返回另一个字符串的长度。 if(str1.length==0) return str2.length; if(str2.length==0) return str1.length;

2.初始化(n+1)*(m+1)的矩阵d，并让第一行和列的值从0开始增长。扫描两字符串（n*m级的），如果：str1[i] == str2[j]，用temp记录它，为0。否则temp记为1。然后在矩阵d[i,j]赋于d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。

3.扫描完后，返回矩阵的最后一个值d[n][m]即是它们的距离。

计算相似度公式：1-它们的距离/两个字符串长度的最大值。

我们用字符串“ivan1”和“ivan2”举例来看看矩阵中值的状况：

1、第一行和第一列的值从0开始增长