- 1LLM之RAG实战(十四)| 利用LongContextRetriver克服RAG中的中间丢失现象_langchain long-context reorder
- 2${pageContext.request.contextPath}不生效的问题_pagecontext.request.contextpath路径失效
- 3Docker(2):利用Docker搭建移动安全测试平台MobSF_mobile-security-framework-mobsf:latest docker
- 4手机端无线投屏技术及方案推荐_无线投屏器方案
- 5Spark机器学习——逻辑回归分类算法_逻辑回归 spark
- 6Credential Provider_credential provider 眼睛
- 7jsp+springboot+java二手车交易管理系统258u6
- 8Android Studio配置阿里云镜像地址,加速依赖资源下载_安卓sdk里面配置镜像加速
- 9Stable Diffusion本地部署报错解决:RuntimeError: Couldn‘t determine Stable Diffusion‘s hash: xxxxxxx_runtimeerror: couldn't fetch stable diffusion.
- 10matlab vgg图像风格迁移,GitHub - AaronJny/nerual_style_change: 使用VGG19迁移学习实现图像风格迁移。...
【机器学习与实现】线性回归示例——波士顿房价分析
赞
踩
一、创建Pandas对象并查看数据的基本情况
boston.csv数据集下载:

链接:https://pan.quark.cn/s/fc4b2415e371
提取码:ZXjU
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
house = pd.read_csv("boston.csv")
print("shape=", house.shape)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
shape= (506, 14)
- 1
house[:5]
- 1
house.describe()
- 1
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | MEDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 |
| mean | 3.593761 | 11.363636 | 11.136779 | 0.069170 | 0.554695 | 6.284634 | 68.574901 | 3.795043 | 9.549407 | 408.237154 | 18.455534 | 356.674032 | 12.653063 | 22.532806 |
| std | 8.596783 | 23.322453 | 6.860353 | 0.253994 | 0.115878 | 0.702617 | 28.148861 | 2.105710 | 8.707259 | 168.537116 | 2.164946 | 91.294864 | 7.141062 | 9.197104 |
| min | 0.006320 | 0.000000 | 0.460000 | 0.000000 | 0.385000 | 3.561000 | 2.900000 | 1.129600 | 1.000000 | 187.000000 | 12.600000 | 0.320000 | 1.730000 | 5.000000 |
| 25% | 0.082045 | 0.000000 | 5.190000 | 0.000000 | 0.449000 | 5.885500 | 45.025000 | 2.100175 | 4.000000 | 279.000000 | 17.400000 | 375.377500 | 6.950000 | 17.025000 |
| 50% | 0.256510 | 0.000000 | 9.690000 | 0.000000 | 0.538000 | 6.208500 | 77.500000 | 3.207450 | 5.000000 | 330.000000 | 19.050000 | 391.440000 | 11.360000 | 21.200000 |
| 75% | 3.647422 | 12.500000 | 18.100000 | 0.000000 | 0.624000 | 6.623500 | 94.075000 | 5.188425 | 24.000000 | 666.000000 | 20.200000 | 396.225000 | 16.955000 | 25.000000 |
| max | 88.976200 | 100.000000 | 27.740000 | 1.000000 | 0.871000 | 8.780000 | 100.000000 | 12.126500 | 24.000000 | 711.000000 | 22.000000 | 396.900000 | 37.970000 | 50.000000 |
house.info()
- 1

二、使用皮尔逊相关系数分析特征之间的相关性
house.corr(method='pearson')
- 1
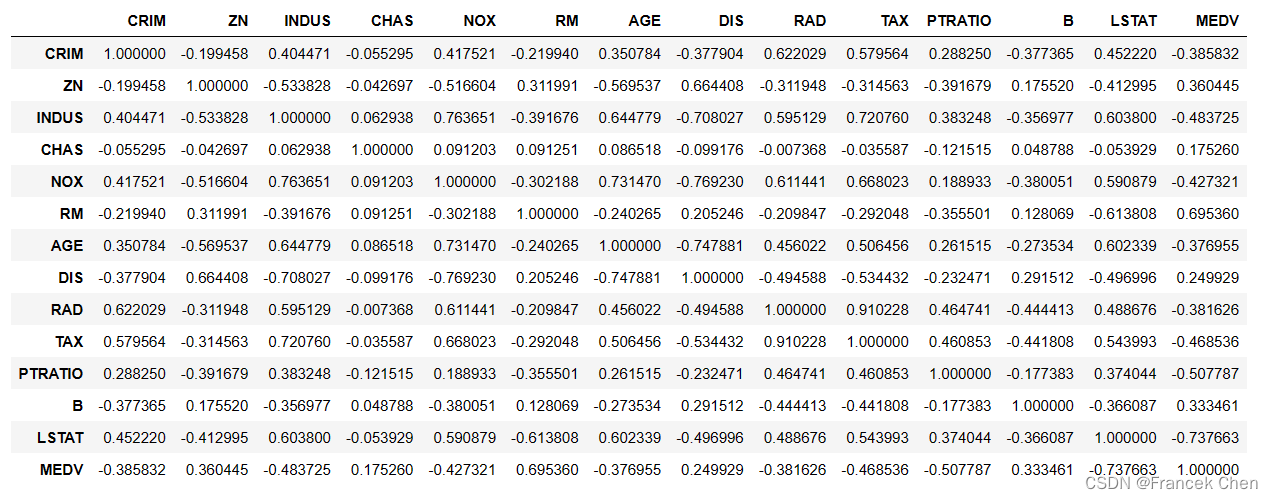
三、可视化不同特征与因变量’MEDV’(房价中值)间的相关性
#可视化不同特征与因变量'MEDV'(房价中值)间的相关性 fig = plt.figure( figsize=(8, 8), dpi=100 ) plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False plt.subplots_adjust(hspace=0.35) plt.subplot(2, 2, 1) #s指定点的大小,可用help(plt.scatter)查看帮助 plt.scatter(house['RM'], house['MEDV'], s=1, marker='o', label='RM-MEDV') plt.xlabel( r"房间数 - $RM$" ) plt.ylabel( r"房价 - $MEDV$" ) plt.title(r"$\rho=0.695360$") plt.subplot(2, 2, 2) plt.scatter(house['LSTAT'], house['MEDV'], s=1, marker='o', label='LSTAT-MEDV') plt.xlabel( r"低层人口比例 - $LSTAT$" ) plt.title(r"$\rho=-0.737663$") plt.subplot(2, 2, 3) plt.scatter(house['DIS'], house['MEDV'], s=1, marker='o', label='DIS-MEDV') plt.xlabel( r"距就业中心距离 - $DIS$" ) plt.ylabel( r"房价 - $MEDV$" ) plt.title(r"$\rho=0.249929$") plt.subplot(2, 2, 4) plt.scatter(house['CHAS'], house['MEDV'], s=1, marker='o', label='CHAS-MEDV') plt.xlabel( r"河景房 - $CHAS$" ) plt.title(r"$\rho=0.175260$") plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
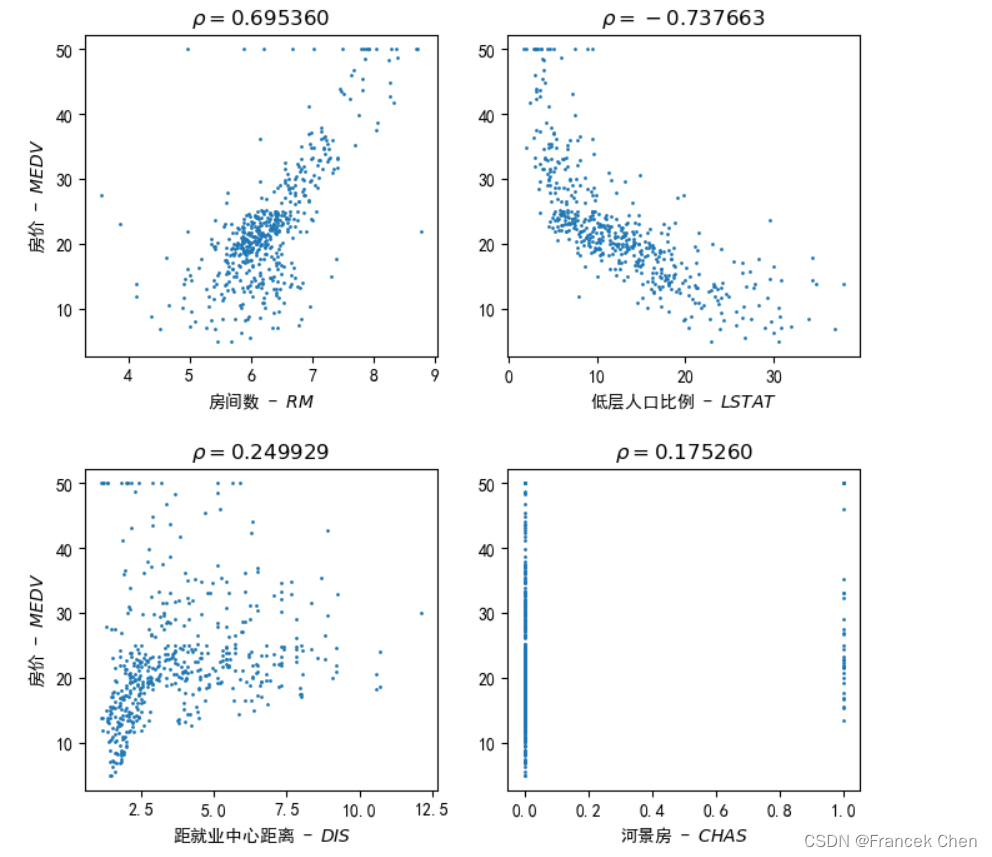
选取特征’RM’(房间数),‘LSTAT’(低层人口比例),‘CHAS’(河景房)和目标’MEDV’(房价中值)形成样本数据。
house1 = house[['RM','LSTAT','CHAS','MEDV']]
house1[:5]
- 1
- 2
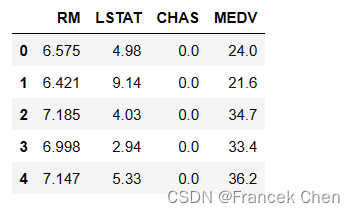
如有必要,对数值型特征进行标准化。
在标准化之前,要使用MinMaxScaler进行特征缩放,这是一个常用的预处理步骤,有助于将数据缩放到一个指定的范围内,通常是[0,1]。
from sklearn.preprocessing import MinMaxScaler
mmScaler = MinMaxScaler() #创建MinMaxScaler对象
mmScaler.fit(house1[['RM','LSTAT']]) #对MinMaxScaler对象进行拟合,以便获取特征的最小值和最大值
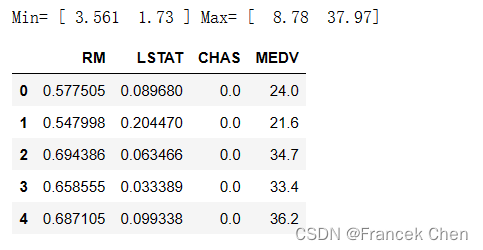
print("Min=", mmScaler.data_min_, "Max=", mmScaler.data_max_)
m = mmScaler.transform(house1[['RM','LSTAT']]) #使用拟合好的MinMaxScaler对象对数据集进行特征缩放
# m = mmScaler.fit_transform(house1[['RM','LSTAT']])
# 创建一个DataFrame来存储特征缩放后的数据,同时保留原始特征'CHAS'和目标变量'MEDV'
house2m = pd.DataFrame(m, columns=['RM','LSTAT'])
house2m[['CHAS','MEDV']] = house1[['CHAS','MEDV']]
house2m[:5]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
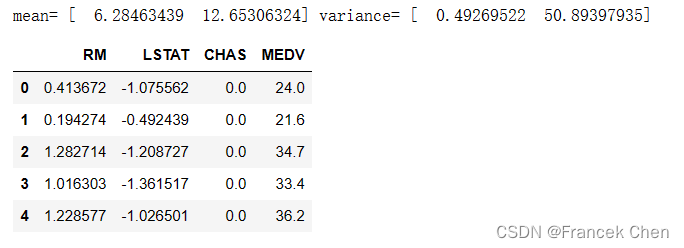
使用 scikit-learn 中的StandardScaler对数据集中的特征进行标准化处理。首先,使用fit方法将标准化器适配到数据上,并打印出了每个特征的均值和方差。然后,使用transform方法对数据进行转换,将标准化后的数据保存到变量z中。接着,将标准化后的特征数据与原始数据集中的其他列(比如CHAS和MEDV)一起合并到新的DataFrame house2z中。
from sklearn.preprocessing import StandardScaler
zScaler = StandardScaler() #创建一个StandardScaler对象
zScaler.fit(house1[['RM','LSTAT']]) #使用fit方法将StandardScaler对象适配到房屋数据的'RM'和'LSTAT'特征上,并计算它们的均值和方差
print("mean=", zScaler.mean_, "variance=", zScaler.var_)
z = zScaler.transform(house1[['RM','LSTAT']]) #使用标准化器对'RM'和'LSTAT'特征进行标准化处理,并保存到变量z中
# z = zScaler.fit_transform(house1[['RM','LSTAT']])
# 创建一个新的DataFrame 'house2z'来保存标准化后的特征数据,并将'CHAS'和'MEDV'列添加到其中
house2z = pd.DataFrame(z, columns=['RM','LSTAT'])
house2z[['CHAS','MEDV']] = house1[['CHAS','MEDV']]
house2z[:5]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
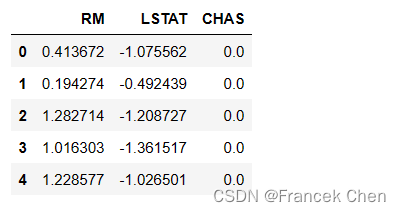
X = house2z[['RM','LSTAT','CHAS']]
X[:5]
- 1
- 2
Y = house2z['MEDV']
Y[:5]
- 1
- 2

四、划分训练集和测试集并进行回归分析
1、划分训练集和测试集
使用train_test_split()函数用于按一定比例划分训练集和测试集。
from sklearn.model_selection import train_test_split
# X为特征数据,Y为目标数据
# test_size参数指定测试集的比例,这里设置为0.2表示测试集占总数据集的20%
# random_state参数用于设置随机种子,相同的值得到相同的训练集和测试集划分
X_train,X_test,Y_train,Y_test = train_test_split(
X, Y, test_size=0.2, random_state=2020)
# 打印训练集和测试集的形状(样本数,特征数或目标数)
print("X_train:", X_train.shape, "Y_train:", Y_train.shape)
print("X_test:", X_test.shape, "Y_test:", Y_test.shape)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9

#help(train_test_split)
- 1
2、创建线性回归模型并拟合训练数据
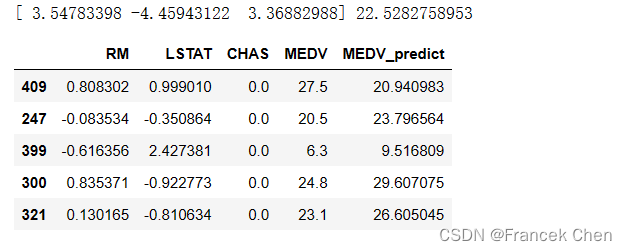
lr.coef_ 是模型的系数,lr.intercept_ 是模型的截距。将测试数据集的前五个样本用于预测,并将预测结果与实际值一起打印出来。这样可以比较模型的预测效果。
from sklearn.linear_model import LinearRegression
#创建LinearRegression估计器对象
lr = LinearRegression()
lr.fit(X_train, Y_train)
print(lr.coef_, lr.intercept_)
XY_test = X_test[:5].copy()
XY_test['MEDV'] = Y_test[:5]
XY_test['MEDV_predict'] = lr.predict(X_test[:5])
XY_test
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
3、创建线性回归模型并用训练集数据进行拟合
接下来,计算训练集和测试集上的R方值(决定系数)和均方误差(MSE)来评估模型的性能。R方值越接近1,表示模型拟合得越好;而均方误差越小,表示模型的预测结果与实际值之间的偏差越小。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
lr.fit(X_train, Y_train); print(lr.coef_, lr.intercept_)
print("训练集R方:%f," % lr.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, lr.predict(X_train)))
print("测试集R方:%f," % lr.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, lr.predict(X_test)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11

#help(lr.score)
#help(mean_squared_error)
- 1
- 2
4、使用K折交叉验证来评估线性回归模型的性能
在每个折叠中,数据被分成训练集和测试集,模型在训练集上进行拟合,并在测试集上进行评估。这有助于更准确地评估模型的泛化能力。在每次迭代中,打印了训练集和测试集的索引,拟合模型的系数和截距,以及模型在测试集上的R方值和均方误差。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
from sklearn.model_selection import KFold
kf = KFold(n_splits=3); n = 0
for train_index, test_index in kf.split(X):
n += 1
print(n, ":TRAIN", train_index.shape, " TEST", test_index.shape)
X1_train, X1_test = X.iloc[train_index], X.iloc[test_index]
Y1_train, Y1_test = Y.iloc[train_index], Y.iloc[test_index]
lr.fit(X1_train, Y1_train); print(lr.coef_, lr.intercept_)
print("测试集R方:%f," % lr.score(X1_test, Y1_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y1_test, lr.predict(X1_test)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15

下面使用带有随机重排和指定随机种子的K折交叉验证来评估线性回归模型。在每个折叠中,将数据分为训练集和测试集,并在训练集上拟合模型。
from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error lr = LinearRegression() coef = [0, 0, 0]; intercept = 0 from sklearn.model_selection import KFold kf = KFold(n_splits=3, shuffle=True, random_state=2020); n = 0 for train_index, test_index in kf.split(X): n += 1 X1_train, X1_test = X.iloc[train_index], X.iloc[test_index] Y1_train, Y1_test = Y.iloc[train_index], Y.iloc[test_index] lr.fit(X1_train, Y1_train) coef += lr.coef_; intercept += lr.intercept_ lr.coef_ = coef/n; lr.intercept_ = intercept/n print(lr.coef_, lr.intercept_) print("训练集R方:%f," % lr.score(X_train, Y_train), end='') print("训练集MSE:%f" % mean_squared_error( Y_train, lr.predict(X_train))) print("测试集R方:%f," % lr.score(X_test, Y_test), end='') print("测试集MSE:%f" % mean_squared_error( Y_test, lr.predict(X_test)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22

5、使用岭回归模型(Ridge)来拟合数据
使用岭回归模型(Ridge)来拟合数据,并计算了模型在训练集和测试集上的R方和均方误差(MSE)。岭回归是一种常见的线性回归的正则化方法,通过引入L2范数惩罚项来控制模型的复杂度,有助于解决特征多重共线性问题。
设置alpha参数为1.0,这是岭回归中控制正则化强度的参数。较大的alpha值意味着更强的正则化。打印岭回归模型的系数(coef)和截距(intercept),以及在训练集和测试集上的R方和MSE。
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
rd = Ridge(alpha=1.0)
rd.fit(X_train, Y_train)
print(rd.coef_, rd.intercept_)
print("训练集R方:%f," % rd.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, rd.predict(X_train)))
print("测试集R方:%f," % rd.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, rd.predict(X_test)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12

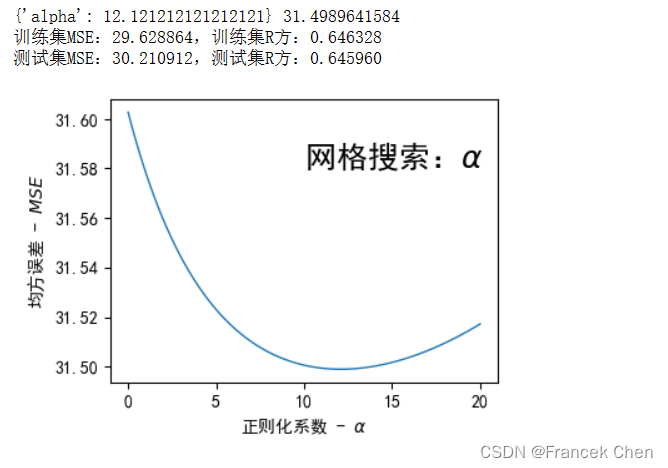
下面使用网格搜索(GridSearchCV)来对岭回归(Ridge)模型的正则化参数alpha进行优化,并绘制了正则化系数与交叉验证的均方误差(MSE)之间的关系。
- 使用
GridSearchCV来搜索不同的alpha值,并选出导致最低均方误差的最佳参数。 - 指定
lamda = np.linspace(0, 20, 100)作为网格搜索的候选参数范围。 scoring='neg_mean_squared_error'表示用负均方误差作为评分标准。cv=3表示使用3折交叉验证来评估每个alpha值的表现。
还计算了最佳参数对应的训练集和测试集上的R方(r2_score)和均方误差(neg_mean_squared_error)。最后,用一幅图展示了不同alpha值对应的交叉验证均方误差,以便直观地了解正则化强度与模型表现之间的关系。
from sklearn.linear_model import Ridge from sklearn.metrics import r2_score rd = Ridge() from sklearn.model_selection import GridSearchCV lamda = np.linspace(0, 20, 100) grid = {'alpha': lamda} gs = GridSearchCV(estimator=rd, param_grid=grid,\ scoring='neg_mean_squared_error', cv=3) gs.fit(X_train, Y_train) print(gs.best_params_, -gs.best_score_) print("训练集MSE:%f," % -gs.score(X_train, Y_train), end='') print("训练集R方:%f" % r2_score( Y_train, gs.predict(X_train))) print("测试集MSE:%f," % -gs.score(X_test, Y_test), end='') print("测试集R方:%f" % r2_score( Y_test, gs.predict(X_test))) fig = plt.figure( figsize=(4, 3), dpi=100 ) plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False plt.plot(lamda, -gs.cv_results_['mean_test_score'], linewidth=1) plt.text(10, 31.58, r"网格搜索:$\alpha$", fontsize=18) plt.xlabel( r"正则化系数 - $\alpha$" ) plt.ylabel( r"均方误差 - $MSE$" ) plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
6、使用Lasso回归防止过拟合
使用了Lasso回归模型,该模型是线性回归的变体,带有L1正则化项。Lasso回归通过缩小回归系数的绝对值来防止过拟合,最终可能导致一些系数变为零,从而实现特征选择的效果。
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
# 创建了一个Lasso模型,正则化参数alpha=1.0,最大迭代次数max_iter=1000
las = Lasso(alpha=1.0, max_iter=1000)
las.fit(X_train, Y_train)
print(las.coef_, las.intercept_) #训练模型后,输出模型的系数和截距
# 计算训练集和测试集上的R方(score方法)和均方误差(mean_squared_error)
print("训练集R方:%f," % las.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, las.predict(X_train)))
print("测试集R方:%f," % las.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, las.predict(X_test)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12

下面将多项式特征扩展与Lasso回归结合。
PolynomialFeatures:这个类用于生成多项式特征,它将输入特征的所有可能的组合作为新的特征。在这里,使用PolynomialFeatures(2, include_bias=False)创建了一个二次多项式特征扩展对象,并将其应用于训练集和测试集,得到了扩展后的特征矩阵X_train_pf和X_test_pf。Lasso:这是Lasso回归模型的调用,使用默认参数alpha=1.0和max_iter=1000。然后,使用扩展后的特征矩阵X_train_pf对模型进行拟合。- 输出模型系数和截距:打印了模型的系数和截距,这些系数对应于扩展后的特征空间中的每个特征。
- 训练集和测试集上的评估:最后,分别计算了训练集和测试集上的R方值和均方误差。R方值(决定系数)用于评估模型对目标变量的拟合程度,均方误差则衡量了模型的预测误差大小。
from sklearn.linear_model import Lasso from sklearn.metrics import mean_squared_error from sklearn.preprocessing import PolynomialFeatures poly = PolynomialFeatures(2, include_bias=False) X_train_pf = poly.fit_transform(X_train) X_test_pf = poly.fit_transform(X_test) # X_train的形状是(样本数, 特征数),而X_train_pf的形状是(样本数, 扩展后的特征数) print("X_train:", X_train.shape, ",X_train_pf.shape:", X_train_pf.shape) las = Lasso(alpha=1.0, max_iter=1000) las.fit(X_train_pf, Y_train) print(las.coef_, las.intercept_) #模型的系数和截距 # 训练集和测试集上的R方值和均方误差 print("训练集R方:%f," % las.score(X_train_pf, Y_train), end='') print("训练集MSE:%f" % mean_squared_error(Y_train, las.predict(X_train_pf))) print("测试集R方:%f," % las.score(X_test_pf, Y_test), end='') print("测试集MSE:%f" % mean_squared_error(Y_test, las.predict(X_test_pf)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19




