机器学习——神经网络（BP）_bp神经网络输入和输出

一.理论基础

BP (Back Propagation) 神经网络是 1986 年由 Rumelhart 和 McClelland 为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络。

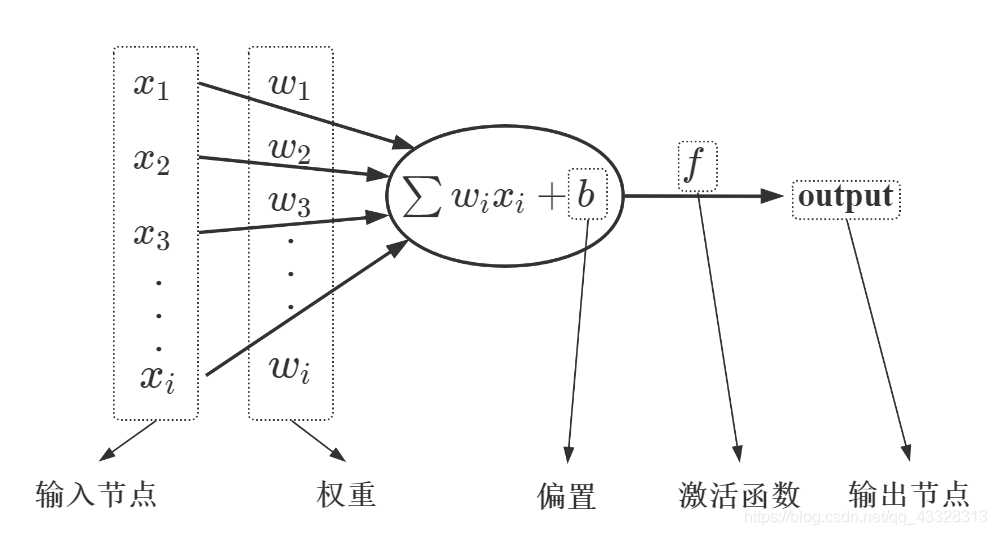
感知器——BP 神经网络中的单个节点

• [ ] 由输入项、权重、偏置、激活函数、输出组成。

• 输入节点：x1​，x2​，x3​，...，xi​

• 权重：w1​，w2​，w3​，...，wi​

• 偏置：b

• 激活函数：f

• 输出节点：output

二.BP神经网络的结构与传播规则

BP 神经网络是一种典型的非线性算法。

BP 神经网络由 输入层、隐含层（也称中间层）和 输出层 构成 ，其中隐含层有一层或者多层。每一层可以有若干个节点。层与层之间节点的连接状态通过 权重 来体现。

只有一个隐含层：传统的浅层神经网络；有多个隐含层：深度学习的神经网络。

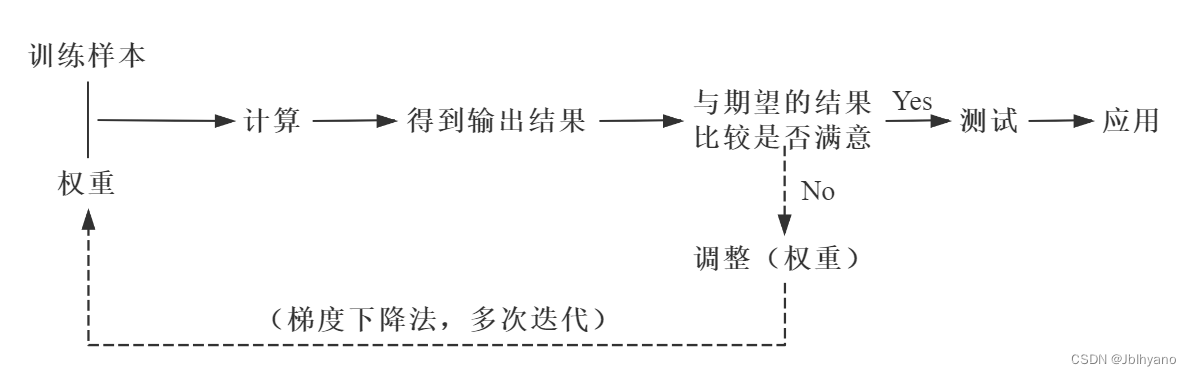
BP 神经网络的核心步骤如下。其中，实线代表正向传播，虚线代表反向传播。

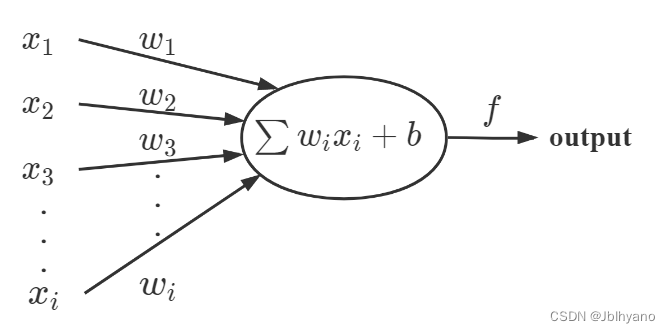
• 正向传播数据（信息、信号）从输入端输入后，沿着网络的指向，乘以对应的权重后再加和，再将结果作为输入在激活函数中计算，将计算的结果作为输入传递给下一个节点。依次计算，直到得到最终结果。通过每一层的感知器，层层计算，得到输出，每个节点的输出作为下一个节点的输入。这个过程就是正向传播。

• 

• 反向传播将输出的结果与期望的输出结果进行比较，将比较产生的误差利用网络进行反向传播，本质是一个“负反馈”的过程。通过多次迭代，不断地对网络上的各个节点间的权重进行调整（更新），权重的调整（更新）采用梯度下降法。

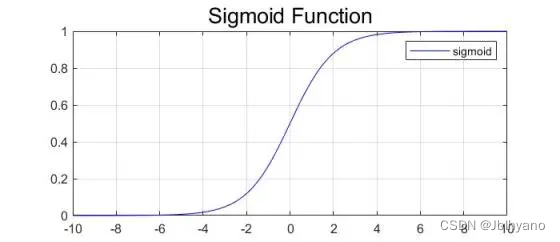
• sigmoid 函数

• δ(x)=1+e−x1​

  • 特点：

    dxdδ(x)​=[1−δ(x)]⋅δ(x)

三.梯度下降学习法

在正向传播的过程中，有一个 与期望的结果比较是否满意 的环节，在这个环节中实际的输出结果与期望的输出结果之间就会产生一个误差，为了减小这个误差，这也就转换为了一个优化过程，对于任何优化问题，总是会有一个目标函数 (objective function)，这个目标函数就是 损失函数（Loss function）。

Loss=21​i=1∑n​(yi​−y^​i​)2=21​i=1∑​[yi​−(wxi​+b)]2

为了让实际的输出结果与期望的输出结果之间的误差最小，就要寻找这个函数的最小值。

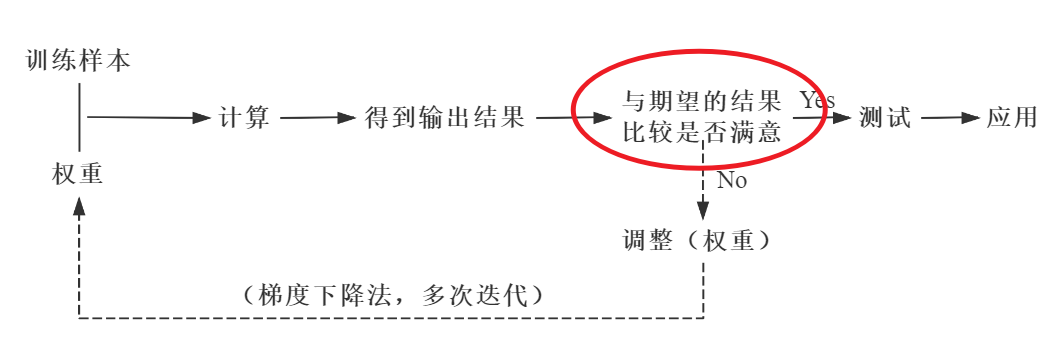
▲ BP神经网络的核心步骤

通过迭代的方法寻找函数最小值

解析解：通过严格的公示推倒计算，给出的方程的精确解，任意精度下满足方程。数值解：在一定条件下，通过某种近似计算得到的解，能够在给定的精度下满足方程。迭代的方法寻找函数最小值 就是通过 梯度下降 + 迭代 的方式寻找数值解。

每一次迭代就会产生一次权重更新，之后将更新的权重与训练样本进行正向传播，如果得到的结果不满意，则进行反向传播，继续迭代。如此往复，直到得到满意的结果为止。

梯度下降学习法，有些像高山滑雪运动员总是在寻找坡度最大的地段向下滑行。当他处于 A 点位置时，沿最大坡度路线下降，达到局部极小点，则停止滑行；如果他是从 B 点开始向下滑行，则他最终将达到全局最小点。

                                                           误差函数梯度下降示意图

BP 神经网络反向传播为什么选择梯度下降法？

梯度下降法是训练神经网络和线性分类器的一种普遍方法。斜率是函数的导数。

在实际上，x 可能不是一个标量，而是一个矢量。参考多元函数的知识，梯度就是偏导数组成的矢量。梯度上的每个元素都会指明函数在该点处各个方向的斜率，因此梯度指向函数变化最快的方向。即指向变大最快的方向和变小最快的方向，对应正梯度和负梯度。

很多深度学习其实都是在计算梯度，然后通过梯度进行迭代，更新参数向量。

四.代码实现

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
#读取数据
data=pd.read_csv('D:\\iris.csv')
print(data)
 
data=data.drop('Unnamed: 0',axis=1)
print(data)
 
print(data.info)
 
#将离群值置为临界值
def std_data(data):
    #计算标准差
    std=data['sepal_width'].std()
    new_sw=[]
    for item in data['sepal_width']:
        if item <=3*std or item>=-3*std:
            new_sw.append(item)
        if item >3*std:
            #将离群值赋给极端值，追加到新列表中
            item=3*std
            new_sw.append(item)
        else:
            item=-3*std
            new_sw.append(item)
    new_sepal_width=pd.DataFrame(new_sw)
    data['new_sepal_width']=new_sepal_width
    return data
new_data=std_data(data)
print(new_data)
 
#空值处理
#method:插值方式，默认为‘ffill',向前填充，或是向下填充
#’bfill‘:向后填充，或是向上填充
new_data.fillna(method='ffill',inplace=True)
 
x_=new_data.drop('target',axis=1)
y_=new_data['target']
'''
sklearn.preprocessing
MinMaxScaler
归一到 [ 0，1 ] 
fit_transform(x_)：训练加改变一次性
'''
from sklearn.preprocessing import MinMaxScaler
X_1=MinMaxScaler().fit_transform(x_)
plt.scatter(X_1[:,0],X_1[:,2],c=y_,cmap=plt.cm.cool)
plt.show()
 
#数据集划分
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(X_1,y_,test_size=0.25)
'''
MLPClassifier:做分类
MLPRegressor:做回归
'''
from sklearn.neural_network import MLPClassifier
mlp=MLPClassifier(hidden_layer_sizes=(100,2),
                  #默认不写的时候是一层的，如果写出（100，2）,则100是节点数，2是两个隐藏层
                  activation='logistic',max_iter=1000)
'''
                    #activation='logistic':隐藏层所加的处理函数，对中间数据进行处理，
                    # 前几层使用logistic函数，防止梯度弥散或者梯度消失
                    #max_iter:最大的迭代次数为1000
'''
mlp.fit(x_train,y_train)
 
ypred=mlp.predict(x_test)
print(ypred)
 
#F1指标
from sklearn.metrics import f1_score
#average='micro':不写的时候默认是单分类，micro是多分类
f1=f1_score(y_test,ypred,average='micro')
print(f1)
 

 总结

• BP 神经网络传播过程包括正向传播和反向传播，其中反向传播本质上是 “负反馈” 。这一点就类似于控制里面的闭环系统，通过反馈，利用偏差纠正偏差，从而达到满意的输出效果；

• 对于误差的处理，利用了 梯度下降法+多次迭代 的方式，寻找最小的误差。在此过程中，每进行一次迭代，不同层节点之间的权重就会发生一次更新。正因为权重的动态更新，每一次正向传播所得到的误差也在动态更新，直至得到期望的输出效果；

• 原理的掌握是基础，代码的实现是关键。文末 9 行代码实现的 BP 神经网络，用简洁的代码反映了 BP 神经网络的原理，是一种单神经网络（simple-neural-network），如果要实现多神经网络，可能就很复杂了。