粒子群算法_粒子群算法的优缺点

一.粒子群算法的简介

粒子群算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，灵感源自于鸟群或鱼群等群体行为观察。该算法通过模拟粒子在搜索空间中的飞行行为，利用个体的历史经验和群体信息进行搜索和优化。在粒子群算法中，每个个体被表示为一个粒子，并具有自身的位置和速度。每个粒子根据自身的历史最优位置（即个体最优）和群体中最优位置（即全局最优）来更新自己的速度和位置，以寻找更好的解。通过迭代搜索，粒子群逐渐聚集在最优解附近，以求得问题的最优解。粒子群算法具有简单易实现、全局搜索能力强、对多维空间的优化效果好等特点，被广泛应用于函数优化、组合优化、机器学习等领域。

二.粒子群算法的基本思想

2.1PSO是通过模拟鸟群或鱼群等群体行为，利用粒子之间的合作和信息共享来寻找问题的最优解。算法通过不断迭代更新粒子的位置和速度，使得粒子逐渐趋向最优解。

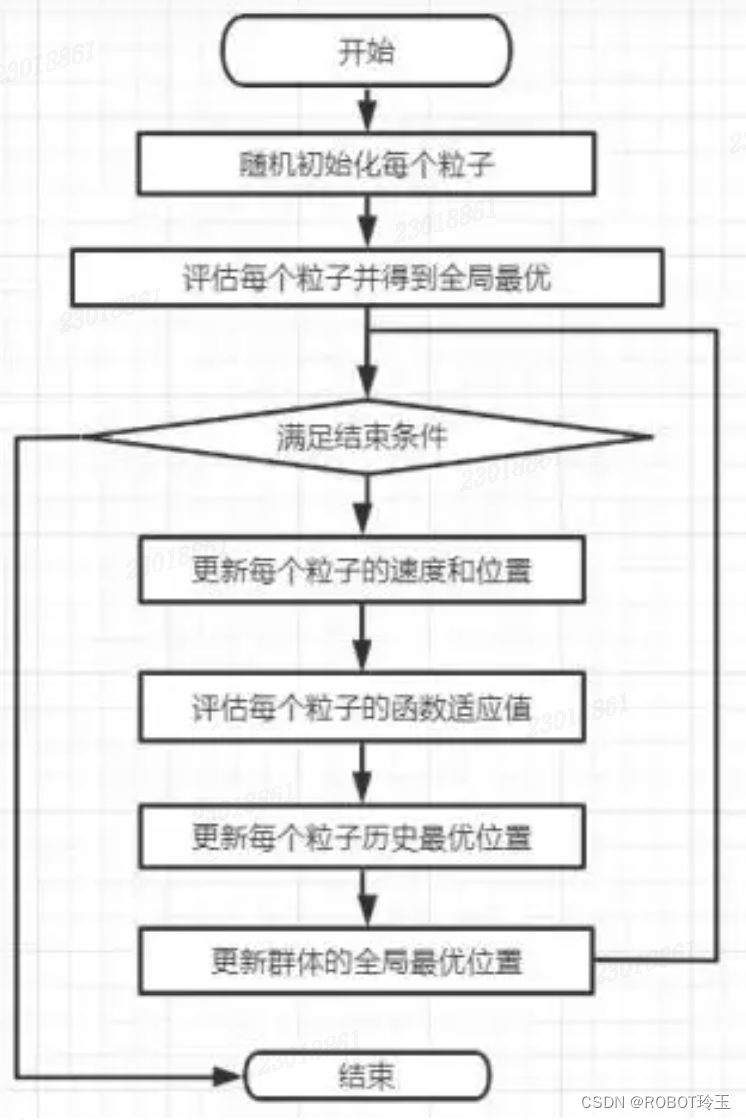
具体来说，粒子群算法包含以下步骤：

1. 初始化粒子群：随机生成一群粒子，并为每个粒子随机分配初始位置和速度。

2. 计算适应度：根据问题的适应度函数，计算每个粒子的适应度值。

3. 更新粒子的个体最优位置：检查每个粒子当前的位置与个体历史最优位置的适应度，若当前位置更优，则更新个体最优位置。

4. 更新群体最优位置：检查所有粒子的个体最优位置，选择适应度最好的位置作为群体最优位置。

5. 更新粒子速度和位置：通过考虑个体历史最优位置和群体最优位置，更新粒子的速度和位置。

6. 判断终止条件：检查是否满足终止条件，例如达到最大迭代次数或找到满意的解。

7. 若不满足终止条件，则回到第3步进行迭代，直到满足终止条件。

在更新粒子速度和位置时，可以使用以下公式进行计算：

速度更新：

v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t)) （1）

位置更新：

x(t+1) = x(t) + v(t+1) （2）

其中，v(t)和x(t)分别表示粒子的当前速度和位置，v(t+1)和x(t+1)表示更新后的速度和位置，pbest表示粒子的个体最优位置，gbest表示群体最优位置，w是惯性权重，c1和c2是加速因子，rand()表示一个在[0,1]范围内的随机数。通过迭代更新，粒子逐渐向最优解靠近，最终找到问题的最优解或接近最优解的解。

2.2算法中的重要参数

在粒子群算法中，一些重要的参数需要根据具体问题和算法效果进行设计和调整。下面是一些常见参数及其设计方法：

1. 粒子数量（Particle Size）：粒子数量决定了算法的搜索范围和计算复杂度。通常，较大的粒子数量可以增加搜索空间的覆盖率和全局搜索能力，但也会增加计算开销。一般来说，粒子数量可以根据问题的复杂度和计算资源进行选择。

2. 惯性权重（Inertia Weight）：惯性权重控制了粒子速度更新中的惯性项，平衡了全局搜索和局部搜索的权衡。较大的惯性权重可以增加全局搜索能力，较小的惯性权重可以增加局部搜索能力。常见的惯性权重更新策略是线性递减或非线性递减，通过调整初始值和衰减率来获取合适的权衡。

3. 加速因子（Acceleration Coefficients）：加速因子包括个体加速因子（c1）和社会加速因子（c2），它们控制了粒子速度更新中的个体最优和群体最优项的贡献。较大的加速因子可以增加搜索的广度，而较小的加速因子可以增加搜索的深度。一般来说，可以根据问题的特性和先验经验来选择和调整加速因子的值。

4. 终止条件（Termination Criterion）：终止条件决定了算法何时停止迭代。常见的终止条件包括达到最大迭代次数、目标函数值收敛或满足一定的精度要求等。终止条件的选择应该符合问题的性质和算法的收敛速度。以上参数的具体设计可根据问题的特性进行调整和优化。可能需要进行多次实验和分析，以找到最佳的参数组合，以获得更好的算法性能和结果。

三 Python实现粒子群算法

当然，下面是一个使用Python进行粒子群算法仿真的具体过程的示例代码：

```python

import random

import numpy as np

# 定义问题函数（此处为二维函数）

def fitness_function(x):

return x[0]**2 + x[1]**2

# 粒子群算法函数

def particle_swarm_optimization(fitness_function, num_particles, max_iterations, search_range):

# 初始化粒子群的位置和速度

particles_position = np.random.uniform(low=search_range[0], high=search_range[1], size=(num_particles, 2))

particles_velocity = np.random.uniform(low=search_range[0], high=search_range[1], size=(num_particles, 2))

# 初始化粒子群的个体最优位置和适应度

particles_best_position = particles_position.copy()

particles_best_fitness = np.array([fitness_function(p) for p in particles_position])

# 初始化全局最优位置和适应度

gbest_index = np.argmin(particles_best_fitness)

global_best_position = particles_best_position[gbest_index]

global_best_fitness = particles_best_fitness[gbest_index]

# 开始迭代

for iteration in range(max_iterations):

# 更新粒子的速度和位置

particles_velocity = 0.7 * particles_velocity \

+ 2 * random.random() * (particles_best_position - particles_position) \

+ 2 * random.random() * (global_best_position - particles_position)

particles_position = particles_position + particles_velocity

# 边界处理

particles_position = np.maximum(particles_position, search_range[0])

particles_position = np.minimum(particles_position, search_range[1])

# 计算粒子的适应度值

particles_fitness = np.array([fitness_function(p) for p in particles_position])

# 更新粒子的个体最优位置和适应度

update_index = particles_fitness < particles_best_fitness

particles_best_position[update_index] = particles_position[update_index]

particles_best_fitness[update_index] = particles_fitness[update_index]

# 更新全局最优位置和适应度

gbest_index = np.argmin(particles_best_fitness)

if particles_best_fitness[gbest_index] < global_best_fitness:

global_best_fitness = particles_best_fitness[gbest_index]

global_best_position = particles_best_position[gbest_index]

# 打印当前迭代的最优解

print(f"Iteration: {iteration+1}, Best Position: {global_best_position}, Best Fitness: {global_best_fitness}")

return global_best_position

# 设置参数

num_particles = 30

max_iterations = 100

search_range = [[-5, 5], [-5, 5]]

# 执行粒子群算法

best_position = particle_swarm_optimization(fitness_function, num_particles, max_iterations, search_range)

# 打印最优解

print(f"Best Position: {best_position}, Best Fitness: {fitness_function(best_position)}")

```这段代码使用随机数生成粒子的位置和速度，并通过迭代更新粒子的速度和位置，最后输出最优解。你可以根据具体问题和需求，修改问题函数和相关参数，使其适应你的实际应用。

四.粒子群算法的优缺点

粒子群算法（PSO）是一种启发式优化算法，具有以下优点和缺点：

优点：

1. 简单易实现：PSO算法的原理较为简单，易于实现，并且不需要求解目标函数的梯度信息。

2. 并行计算能力：PSO算法的计算过程是并行的，不同粒子的位置和速度可以同时更新，因此适用于并行计算环境。

3. 全局搜索能力：通过合作与信息共享，PSO算法能够在搜索空间中全局搜索，对于具有多个局部最优解的问题具有较好的搜索能力。

4. 自适应性：PSO算法中的惯性权重和加速因子可以通过调整来平衡全局搜索和局部搜索的能力，使算法具有一定的自适应性。

缺点：

1. 参数选择困难：PSO算法的性能受到参数的选择和设置影响较大，特别是惯性权重和加速因子的选择往往需要通过试错方式进行调整，增加了算法的实验难度。

2. 可收敛性差：在某些复杂问题中，由于算法的全局搜索能力和局部搜索能力之间的权衡，PSO算法可能在某些情况下会陷入局部最优解，并且难以跳出。

3. 对初始种群敏感：初始粒子群的位置和速度的选择对PSO算法的性能有较大影响，在某些情况下，不合适的初始粒子群可能导致算法无法收敛或很难找到较优解。

需要注意的是，PSO算法并非适用于所有优化问题，它在解决一些连续空间的、没有约束的优化问题时可能效果较好，但在其他类型的问题上可能不如其他优化算法表现好。因此，在选择优化算法时，需要根据具体问题的属性和需求来评估和选择合适的算法。