光线投射之伪3d_光线投射算法伪3d游戏

光线投射是一种在 2D 地图中创建 3D 透视的渲染技术。当计算机速度较慢时，不可能实时运行真正的 3D 引擎，光线投射是第一个解决方案。光线投射可以非常快，因为只需对屏幕的每条垂直线进行计算。

光线投射的基本思想如下：地图是一个 2D 方格网格，每个方格可以是 0（= 无墙），也可以是正值（= 具有特定颜色或纹理的墙）。

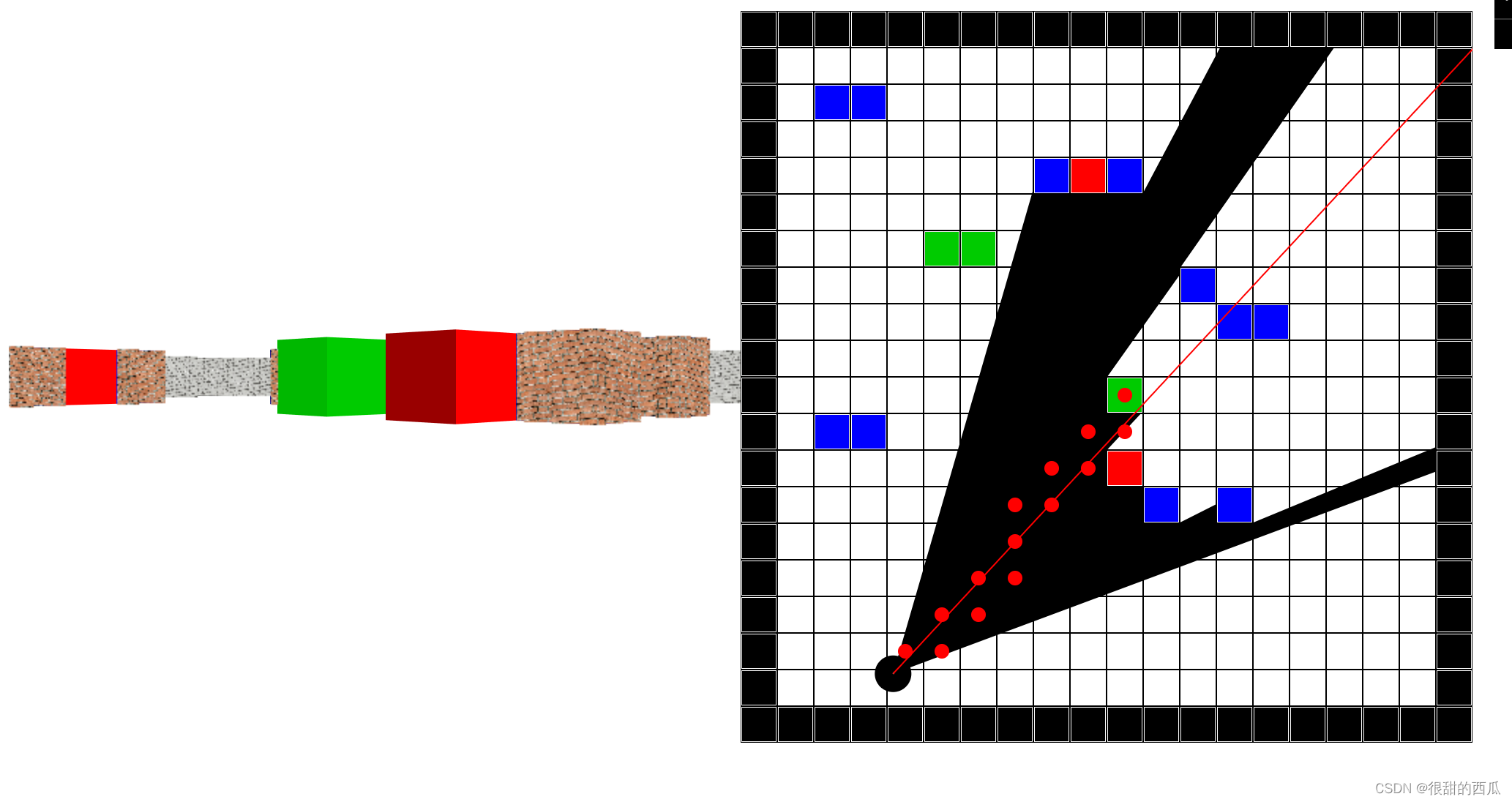
对于屏幕的每个 x（即屏幕的每个垂直条纹），发出一条从玩家位置开始的光线，其方向取决于玩家的观看方向和屏幕的 x 坐标。然后，让这条射线在 2D 地图上向前移动，直到它碰到一个地图方块（即墙）。如果它撞到了墙，计算这个击中点到玩家的距离，并使用这个距离来计算这堵墙必须在屏幕上绘制多高：墙越远，它在屏幕上越小，越近，看起来就越高。这些都是二维计算。此图显示了两条此类光线（红色）的自上而下的概述，它们从玩家（绿点​​）开始并击中蓝色墙壁：

 let rayDirX = Math.cos(theta) // -1 left 1 right
                            let rayDirY = Math.sin(theta) // -1 top 1 bottom
 
                            let cameraX = this.origin.x / cellWidth  // float
                            let cameraY = this.origin.y / cellHeight
 
                            let mapX = cameraX >> 0; // int
                            let mapY = cameraY >> 0;
 
                            // 从相机到当前格子的距离
                            let sideDistX, sideDistY;
                            // 1/cos =dist/dx= sec（正割）
                            // 1/sin =dist/dy =csc (余割)
                            // 计算距离，当x或y行进多少步后，当前距离是多少了
                            // 方便快速计算距离
                            // 保证x轴和y轴两个的步率是一样的
                            /**
                             *  ◿ c=5 a=3 b=4   
                             * cos=4/5, 1/cos=5/4  
                             * sin=3/5, 1/sin=5/3
                            */
                            let deltaDistX = rayDirX === 0 ? 1e30 : Math.abs(1 / rayDirX)
                            let deltaDistY = rayDirY === 0 ? 1e30 : Math.abs(1 / rayDirY)
 
                            let stepX, stepY;
 
                            // 侧面距离
                            if (rayDirX < 0) {
                                // 光线朝右
                                stepX = -1
                                // 当前相机距离当前格子距离是多少
                                sideDistX = (cameraX - mapX) * deltaDistX
                            } else {
                                stepX = 1
                                // 下一个格子，左侧距离相机距离是多少
                                sideDistX = (mapX + 1 - cameraX) * deltaDistX
                            }
                            // 正面，距离
                            if (rayDirY < 0) {
                                // 光线朝下
                                stepY = -1
                                // 当前相机距离当前格子距离是多少
                                sideDistY = (cameraY - mapY) * deltaDistY
                            } else {
                                stepY = 1;
                                // 下一个格子，左侧距离相机距离是多少
                                sideDistY = (cameraY + 1 - mapY) * deltaDistY
                            }
 
                            let isCollided = false;
                            let isSide = false // 是否是墙
                            let distance = 0
 
                            // 计算光线投射
                            while (!isCollided) {
                                // 如果横向距离小于纵向距离,就向x轴前进
                                if (sideDistX < sideDistY) {
 
                                    sideDistX += deltaDistX // 更新当前相机与当前格子的侧边距离
                                    mapX += stepX // 移动到左边或右边格子
                                    // 如果光线与侧边距近更近,那就是侧边
                                    isSide = true;
                                } else {
                                    sideDistY += deltaDistY
                                    mapY += stepY // 移动到上边或下边格子
                                    isSide = false;
                                }
                                if (mapY >= map.length || map[mapY][mapX] > 0) {
                                    isCollided = true;
                                }
                            }
                            if (isSide) {
                                distance = sideDistX - deltaDistX
                            } else {
                                distance = sideDistY - deltaDistY
                            }
                            // 是否鱼眼观看
                            // 鱼眼
                            let notFish = true;
                            if (notFish) {
                                distance = distance * Math.cos(theta - startRadian)
                            }
 
                            let lineHeight = canvasHeight / distance
                            // lineHeight=lineHeight*Math.cos(theta - startRadian)
                            // 距离越近物体看起来越高，距离越远看起来越矮
                            let halfCanvasHeight = canvasHeight * 0.5
                            let wallTop = halfCanvasHeight - lineHeight * 0.5
                            let wallBottom = halfCanvasHeight + lineHeight * 0.5
                            wallTop = clamp(wallTop, 0, canvasHeight)
                            wallBottom = clamp(wallBottom, 0, canvasHeight)
 
 
                            // 计算光线投射最终位置
                            let x = this.origin.x + rayDirX * (distance * cellWidth)
                            let y = this.origin.y + rayDirY * (distance * cellHeight)

要找到光线在途中遇到的第一面墙，您必须让它从玩家的位置开始，然后始终检查光线是否在墙内。如果它在墙内（命中），则循环可以停止，计算距离，并以正确的高度绘制墙。如果光线位置不在墙壁内，则必须进一步追踪它：在该光线方向的方向上为其位置添加一定的值，对于这个新位置，再次检查它是否在墙壁内。继续这样做，直到最后撞到墙。

人类可以立即看到光线击中墙壁的位置，但不可能用单个公式找到光线立即击中哪个方块，因为计算机只能检查光线上有限数量的位置。许多光线投射器每一步都会为光线添加一个恒定值，但它有可能会错过墙壁！例如，对于这条红色光线，它的位置在每个红点处都被检查：

人类可以立即看到光线击中墙壁的位置，但不可能用单个公式找到光线立即击中哪个方块，因为计算机只能检查光线上有限数量的位置。许多光线投射器每一步都会为光线添加一个恒定值，但它有可能会错过墙壁！例如，对于这条红色光线，它的位置在每个红点处都被检查：

 

正如你所看到的，光线直接穿过蓝色的墙壁，但计算机没有检测到这一点，因为它只在红色的位置检查点。检查的位置越多，计算机检测不到墙壁的机会就越小，但需要的计算也就越多。这里步距减半，所以现在他检测到光线穿过了墙，

 

为了使用此方法获得无限精度，需要无限小的步长，因此需要无限数量的计算！这很糟糕，但幸运的是，有一种更好的方法，只需要很少的计算，就能检测到每面墙：其想法是检查射线将遇到的墙的每一侧。我们给每个正方形的宽度为 1，因此墙的每一边都是一个整数值，中间的位置在点之后有一个值。现在步长不是恒定的，它取决于到下一侧的距离：

 

正如您在上图中看到的，光线准确地击中了墙壁上我们想要的位置。在本教程中介绍的方式中，使用基于 DDA 或“数字微分分析”的算法。DDA 是一种快速算法，通常用于方形网格，用于查找一条线击中了哪些方形（例如，在屏幕上绘制一条线，屏幕是方形像素的网格）。因此，我们还可以使用它来查找射线击中的地图的哪些方块，并在击中墙体方块后停止算法。

一些光线追踪器使用欧几里德角度来表示玩家和光线的方向，并用另一个角度确定视野。然而，我发现使用向量和相机要容易得多：玩家的位置始终是向量（x 和 y 坐标），但现在，我们也将方向设为向量：所以方向现在是由两个值确定：方向的 x 和 y 坐标。方向向量可以这样理解：如果你沿着玩家看的方向画一条线，穿过玩家的位置，那么这条线的每个点都是玩家位置与方向的倍数之和向量。方向向量的长度并不重要，重要的是它的方向。

这种使用向量的方法还需要一个额外的向量，即相机平面向量。在真正的 3D 引擎中，还有一个相机平面，并且该平面实际上是一个 3D 平面，因此需要两个向量（u 和 v）来表示它。然而，光线投射发生在 2D 地图中，因此这里的相机平面并不是真正的平面，而是一条线，并用单个向量表示。相机平面应始终垂直于方向矢量。相机平面代表计算机屏幕的表面，而方向矢量垂直于相机平面并指向屏幕内部。玩家的位置是一个点，是相机平面前面的一个点。屏幕某个 x 坐标的某条射线就是从该玩家位置开始的射线