贪心算法/贪婪算法_贪心算法和贪婪算法一样吗

        贪心算法是所有算法中最简单、最易实现的一种算法，的吗？

        世界上本没有贪，学算法的人多了，也便有了贪。        你贪我也贪，贪心算法也变得越来越难贪了。       

        但是，万变不离其宗，打好基础得其根本，我想怎么贪，就怎么贪，怎么贪都不怕！！

---

贪心算法简介 

        贪心算法（又称贪婪算法）是一种在求解问题时，做出在某种意义上的局部最优解的算法（作出在当前看来最好的选择。  贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择。

        贪心算法的结果往往都能得到全局最优解，或者是最优解的近似。因此，贪心算法也应用在许多实际问题，例如单源最短路径问题（Dijkstra算法）、最小生成树问题(Kruskal和Prim算法)、粒子群算法和人工蜂群算法……

        以粒子群算法为例：每个粒子寻找当前位置的最优解，最优的个体极值作为整个粒子群的当前全局最优解，重复上述步骤得到问题的全局最优解。

                 

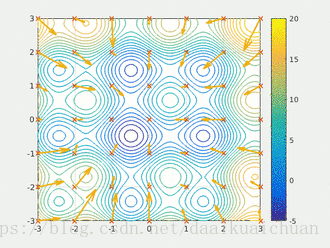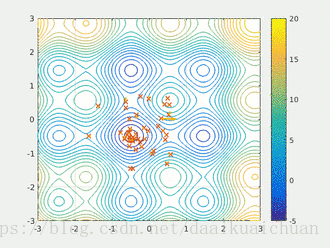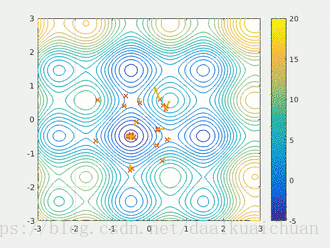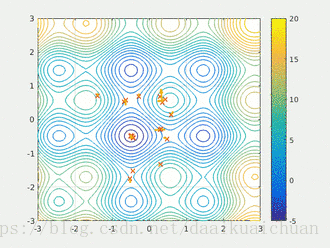
        综上所述，贪心算法解决问题的核心思想是：贪心算法的每一步都是选择当前情况下的局部最优解，进而得到全局最优解。

---

贪心算法基本要素

        1. 贪心选择性质：问题的最优解可以通过贪心选择实现。（贪心选择：通过一系列的局部最优解 ==> 得到全局最优解。  但否具有贪心选择性质，必须证明每一步所作的贪心选择最终指向问题的整体最优解。

        2. 最优子结构性质：问题的最优解包含子问题的最优解。（因为全局最优解是由局部最优解通过贪心选择得到的。

---

贪心算法解题策略（以粒子群为例解释

        1 建立数学模型描述问题（粒子在寻找的全局目标是什么？

        2 把求解的问题分成若干个子问题（相当于有多少个粒子？每个粒子寻找的局部目标是什么？

        3 对每个子问题求解，得到子问题的局部最优解（通过迭代更新得到每个粒子的局部最优解。贪心选择

        4 每个子问题的局部最优解合成原问题的全局最优解（在所有粒子的局部最优解中找到全局最优解。最优子结构 

while(约束条件成立)
{
  选择当前的最优解，记录并累积到最后的解中
  if(当前最优解使用完毕)
    当前最优解 = 当前次优解
}
//来自：解梦者 的 五大算法思想（二）贪心算法及常见例子

         贪心算法的终止条件是：当达到某算法中的某一步不能再继续前进时（得到全局最优解，算法停止。

---

贪心算法例题分析

钱币找零问题

        人民币的面额有100元、50元、10元、5元、2元、1元。所以在找零钱时，有多种方案选择。那么现在给出所要找的钱Total，至少要用多少张纸币？

#include<bits/stdc++.h>
using namespace std;
int main()
{
	//定义变量和初始化 
	int Value[6] = {100,50,20,10,5,1};	//记录钱币面值
	int Amount[6] ={0};			    //记录每种面值的数量
	int Total,Flag = 0,count=0;		//Total-一共要找的零钱  Flag-当前已找的零钱  count-要找的纸币数量 
	//输入
	cout<<"请输入你要找的零钱数："<<endl;
	cin>>Total;
	//进行主循环 寻找全局最优解
	for(int i=0;i<6;)
	{
		//寻找当前能用的最大面值 局部最优解 
		if(Flag+Value[i]>Total)
		{
			i++;
			continue;
		}
		//更新最优解
		Total -= Value[i];    ++Amount[i];    ++count;
		//循环结束条件
		if(!Total)
			break;
	}
	//进行输出循环 每种纸币所需数量 和 最少需要纸币数量 
	for(int i=0;i<6;++i)
	{
		if(Amount[i])
		{
			printf("面值为%d的纸币需要%d张\n",Value[i],Amount[i]);
		}
	}
	printf("最少需要%d张纸币",count); 
	return 0;
}

        零钱找零问题的核心思想就在于：贪心算法每一步都选择的是当前所允许的最大面值的硬币（即局部最优解），整个解决方案也是最优的。 

        但是贪心算法确实不是对所有问题都能得到整体的最优解，如果我们将上述的案例中加入面值为7元的钱币，此时是否还能得到全局最优解呢？

---

5919：活动安排问题

---

5739：部分背包问题

        背包问题指的是在背包所能承受的重量范围内，将哪些物品装入背包可以获得最大的收益？

        在一家商店中，有N种物品，现有1个背包，背包容量为W，每个物品i的价值为pi，重量为wi，如何选择装入物品能使背包的总价值values最大？（此处的背包问题指的是部分背包，不是像0-1背包问题中的某个物品不能拆开，此处的物品可以拆开，选取一部分放入背包中。0-1背包问题用的是动态规划解决，这里先不讲。

#include<bits/stdc++.h>
#define N 5    //设定物品数量 有兴趣的可以改成手动输入
using namespace std;
 
//将物品按照单位重量价值进行排序
void Sort(double weight[], double price[]) 
{ 
    double val[N] = {0};	//用val[]存物品的单位价值 
    for(int i=0;i<N;i++)
        val[i] = price[i]/weight[i];
  
  //对 val[] 进行排序  同时对 weight[] 和 price[] 进行排序 方便后面进行贪心 
    for (int i=0;i<N;i++)  //这里不直接调用sort()库函数是因为要对w和p排序 
    {
        for (int j=i+1;j<N;j++)  //冒泡排序法 
		{
            if(val[i]<val[j]) 
			{
                double temp = val[i];  val[i] = val[j];  val[j] = temp;
                temp = weight[i];  weight[i] = weight[j];  weight[j] = temp;
                temp = price[i];  price[i] = price[j];  price[j] = temp;
            }
        }
    }
}
 
void fractional_knapsack(double weight[], double price[], double rate[], double W) {
	double temp = 0;
    int i = 0;
    //将物品按照单位重量价值进行排序。 
    Sort(weight, price);
 
    //开始进行贪心选择，尽可能多的单位重量价值最高的物品装入背包
	//如果最后一件物品无法全部装入，则计算可以装入的比例，然后按比例装入 
    while (W>0) //有容量 
	{
        temp = W > weight[i]?weight[i]:W;
        rate[i] = temp / weight[i++]; //rate只会<=1 
        W -= temp; //剩余背包容量 
    }
}
 
int main() {
    double values = 0;	//初始化背包的总价值 
    //初始化物品的重量、价值、装入背包比例 有兴趣的可以改成手动输入
    double weight[N] = {10,70,20,90,60};  //各个物品的重量
    double price[N] = {200,30,100,10,20};  //各个物品的价值 
    double rate[N] = {0};  //各个物品装入背包的比例
    
    fractional_knapsack(weight, price, rate, 52.0);  //调用解决部分背包问题的函数
    //根据 rate 数组中记录的数据，决定装入哪些物品
    for (int i=0;i<N;i++) {
        if (rate[i] == 1)
		{
            printf("重量为%.2lf 价值为%.2lf的物品可以完全装入\n", weight[i], price[i]);
            values += price[i];
        }
        else if (rate[i] == 0)
            printf("重量为%.2lf,价值为%.2lf的物品不装入\n", weight[i], price[i]);
        else {
            printf("重量为%.2lf,价值为%.2lf的物品可以被装入的比例是%lf%%\n", weight[i], price[i],rate[i]*100);
            values += price[i] * rate[i];
        }
    }
    printf("背包的总价值为%lf",values);
    return 0;
}

        部分背包问题的核心思想在于：从贪心算法的角度看， 为保证背包中的物品总价值最大，必须确保放入的每件物品的单个价值尽量大。

        部分背包问题的解题步骤大致分为以下三个部分：

1. 将物品按照单位重量价值进行排序。
2. 将尽可能多的单位重量价值最高的物品装入背包。
3. 如果最后一件物品无法全部装入，则计算可以装入的比例，然后按比例装入。

---

5945：区间覆盖问题

---

         想看更多贪心算法例题的，可以看看 linylin的贪心总结1 或者 力扣 ​上看面试题​​​​​​。

---

贪心算法存在问题

        贪心算法从问题的某一个初始解开始出发到逼近最终解，以尽可能快的地求得更好的解，却不从整体最优上加以考虑，使得它存在一定的问题。

        1. 所得到的解不一定是最佳的。

        因为贪心算法每次选取局部最优解，自顶向下，通过迭代进行贪心选择，不进行回溯处理，所以容易陷入局部最优解而得不到全局最优解。

        2. 贪心算法一般用来解决求最大或最小解。

        3. 贪心算法只能确定某些问题的可行性范围。

        贪心算法是有局限性的，只能应用于部分问题的可行性问题。

---

        贪心算法正由于它简单高效，空间复杂度低的特点，省去了寻找最优解可能需要的穷举操作。但也因为贪心算法的缺点使得它不能被完全信赖，所以贪心算法通常作为其它算法的辅助算法来使用。

---