matlab回归问题,机器学习笔记（一）—— 线性回归问题与Matlab求解

给你多组数据集，例如给你很多房子的面积、房子距离市中心的距离、房子的价格，然后再给你一组面积、 距离，让你预测房价。这类问题称为回归问题。

回归问题(Regression) 是给定多个自变量、一个因变量以及代表它们之间关系的一些训练样本，来确定它们的关系。其中最简单的一类是线性回归(Linear Regression)。

线性回归函数的形式如下:

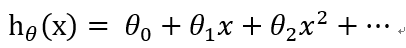  (1)

θj是我们要求的系数。接下来介绍一下求θ 的两种方法，梯度下降(Gradient Descent)和正规方程(Normal Rquation )。

1. 梯度下降法

描述：梯度下降法(Gradient descent)是一个一阶最优化算法，通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点；这个过程则被称为梯度上升法。

公式：

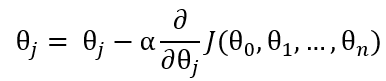(2)

其中，J(θ) 称为代价函数(Cost Function )或损失函数(Loss Function), 用来量度预测结果和标准结果之间的误差，常见的有交叉熵，均方误差，平均绝对值误差等。在这里使用均方误差。α是学习速率，取值自定，一般取比较小的数，如0.0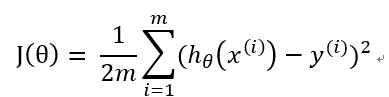3

(3)

( hθ(x) 是x经过待求的函数得出的结果，y(i) 是数据集中的结果)

公式(2)的旨在求出最小的θj，把代价函数J(θ)降到最小。它的原理是θ不停地迭代，减去θ对应的代价函数在x的偏导，如果偏导是正的，那么J(θ)在该方向单增，减去这个正数后θ变小，J(θ)也会跟着变小；反之，如果偏导是负的，J(θ)单减，原θ减负数，θ变大，J(θ)减小。无论怎样,J(θ)都朝着减小的方向变化。值得注意的是，如果学习速率α偏大，那么θ在做差的话可能减过头甚至得到的新J(θ)比原来还要大,而如果学习速率α偏小，那么花费的时间会变长。

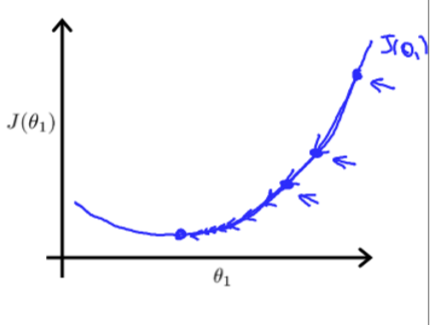(结合图像更直观)

梯度下降算法是一个不断迭代的过程，需要不断重复公式(2)，直到J(θ)符合预期误差或者达到足够的迭代次数。

具体步骤如下：

step0: 初始化α，θ(任意值)和迭代次数；

step1:利用公式(3) ，求J(θ);

step2:利用公式(2)，本次迭代的新θ;

step3:重复step1 - step2

2. 正规方程

利用正规方程可以直接计算计算θ，前提是(XTX)必须可逆

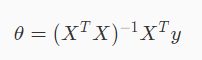
3. matlab实现

3.1 初始化参数

data = load('ex1data1.txt');

X = data(:, 1); y = data(:, 2);

m = length(y); % number of training examples

plotData(X, y)

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x

theta = zeros(2, 1); % initialize fitting parameters

% Some gradient descent settings

iterations = 1500;

alpha = 0.01;

3.2 计算代价函数

function J = computeCost(X, y, theta)

%COMPUTECOST Compute cost for linear regression

%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the

%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values

m = length(y); % number of training examples

% You need to return the following variables correctly

J = 0;

% ====================== YOUR CODE HERE ======================

% Instructions: Compute the cost of a particular choice of theta

%               You should set J to the cost.

predictions = X*theta;

sqrErrors = (predictions - y).^2;

J = 1/(2*m) * sum(sqrErrors);

% =========================================================================

end

3.3 梯度下降并迭代

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)

%GRADIENTDESCENT Performs gradient descent to learn theta

% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by

% taking num_iters gradient steps with learning rate alpha

% Initialize some useful values

m = length(y); % number of training examples

J_history = zeros(num_iters, 1);

x = X(:,2);

for iter = 1:num_iters

% ====================== YOUR CODE HERE ======================

% Instructions: Perform a single gradient step on the parameter vector

% theta.

%

% Hint: While debugging, it can be useful to print out the values

% of the cost function (computeCost) and gradient here.

%

J = alpha * (1/m) * (X * theta - y)' ;

theta(1) = theta(1) - J * ones(m,1);

theta(2) = theta(2) - J * x;

% ============================================================

% Save the cost J in every iteration

J_history(iter) = computeCost(X, y, theta);

end

end

3.4 绘图

% Grid over which we will calculate J

theta0_vals = linspace(-10, 10, 100);

theta1_vals = linspace(-1, 4, 100);

% initialize J_vals to a matrix of 0's

J_vals = zeros(length(theta0_vals), length(theta1_vals));

% Fill out J_vals

for i = 1:length(theta0_vals)

for j = 1:length(theta1_vals)

t = [theta0_vals(i); theta1_vals(j)];

J_vals(i,j) = computeCost(X, y, t);

end

end

% Because of the way meshgrids work in the surf command, we need to

% transpose J_vals before calling surf, or else the axes will be flipped

J_vals = J_vals';

% Surface plot

figure;

surf(theta0_vals, theta1_vals, J_vals)

xlabel('\theta_0'); ylabel('\theta_1');

% Contour plot

figure;

% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100

contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))

xlabel('\theta_0'); ylabel('\theta_1');

hold on;

plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

coursera机器学习笔记-多元线性回归，normal equation

#对coursera上Andrew Ng老师开的机器学习课程的笔记和心得: #注:此笔记是我自己认为本节课里比较重要.难理解或容易忘记的内容并做了些补充,并非是课堂详细笔记和要点: #标记为

Stanford机器学习笔记-1.线性回归

Content: 1. Linear Regression 1.1 Linear Regression with one variable 1.1.1 Gradient descent algorit ...

Andrew Ng机器学习课程笔记--week1(机器学习介绍及线性回归)

title: Andrew Ng机器学习课程笔记--week1(机器学习介绍及线性回归) tags: 机器学习, 学习笔记 grammar_cjkRuby: true --- 之前看过一遍,但是总是模 ...

Python机器学习笔记：不得不了解的机器学习面试知识点(1)

机器学习岗位的面试中通常会对一些常见的机器学习算法和思想进行提问,在平时的学习过程中可能对算法的理论,注意点,区别会有一定的认识,但是这些知识可能不系统,在回答的时候未必能在短时间内答出自己的认识,因 ...

cs229 斯坦福机器学习笔记(一)-- 入门与LR模型

版权声明:本文为博主原创文章,转载请注明出处. https://blog.csdn.net/Dinosoft/article/details/34960693 前言 说到机器学习,非常多人推荐的学习资 ...

机器学习笔记5-Tensorflow高级API之tf.estimator

前言 本文接着上一篇继续来聊Tensorflow的接口,上一篇中用较低层的接口实现了线性模型,本篇中将用更高级的API--tf.estimator来改写线性模型. 还记得之前的文章

【TensorFlow篇】--Tensorflow框架初始，实现机器学习中多元线性回归

一.前述 TensorFlow是谷歌基于DistBelief进行研发的第二代人工智能学习系统,其命名来源于本身的运行原理.Tensor(张量)意味着N维数组,Flow(流)意味着基于数据流图的计算,T ...

Python机器学习笔记：sklearn库的学习

网上有很多关于sklearn的学习教程,大部分都是简单的讲清楚某一方面,其实最好的教程就是官方文档. 官方文档地址:https://scikit-learn.org/stable/ (可是官方文档非常 ...

Python机器学习笔记：不得不了解的机器学习知识点(2)

之前一篇笔记: Python机器学习笔记:不得不了解的机器学习知识点(1) 1,什么样的资料集不适合用深度学习? 数据集太小,数据样本不足时,深度学习相对其它机器学习算法,没有明显优势. 数据集没有局 ...

随机推荐

Tensorflow二分类处理dense或者sparse(文本分类)的输入数据

这里做了一些小的修改,感谢谷歌rd的帮助,使得能够统一处理dense的数据,或者类似文本分类这样sparse的输入数据.后续会做进一步学习优化,比如如何多线程处理. 具体如何处理sparse 主要是使 ...

日历组件的使用，bootstrap-datetimepicker

官方文档:http://www.bootcss.com/p/bootstrap-datetimepicker/ .html