数学建模【对粒子群算法中惯性权重和学习因子的改进】_粒子群算法惯性因子

一、改进原因

这是前面 数学建模【粒子群算法】 中的一部分，这里提到了w存在的一些问题，那么本篇介绍一些方法对w和因子进行一些改进，提高粒子群算法的效率和准确度。

二、改进方法

1.线性递减惯性权重

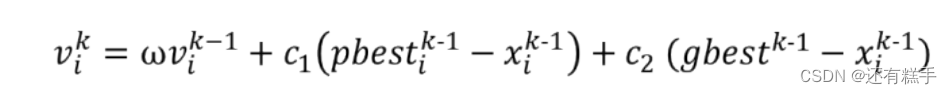
惯性权重w体现的是粒子继承先前的速度的能力，Shi,Y最先将惯性权重w引入到粒子群算法中，并分析指出一个较大的惯性权值有利于全局搜索，而一个较小的权值则更利于局部搜索。为了更好地平衡算法的全局搜索以及局部搜索能力，Shi,Y提出了线性递减惯性权重LDIW（Linear Decreasing Inertia Weight），公式如下：

其中d是当前迭代的次数，K是迭代总次数。

wstart一般取0.9，wend一般取0.4。与原来的相比，现在的惯性权重和迭代次数有关。

参考论文：Shi, Y. and Eberhart, R.C. (1999) Empirical Study of Particle Swarm Optimization. Proceedings of the 1999 Congress on Evolutionary Computation, Washington DC, 6-9 July 1999, 1945- 1950.

既然有线性递减惯性权重，那肯定也有非线性递减惯性权重。

在网上找到结果非常多，这里给出常用的两个：

2.自适应惯性权重

假设现在求最小值问题，那么：

一个较大的惯性权值有利于全局搜索，而一个较小的权值则更利于局部搜索。

假设现在一共五个粒子ABCDE，此时它们的适应度分别为1，2，3，4，5。取最大惯性权重为0.9，最小惯性权重为0.4。那么，这五个粒子的惯性权重应该为：0.4，0.65，0.9，0.9，0.9。适应度越小，说明距离最优解越近，此时更需要局部搜索；适应度越大，说明距离最优解越远，此时更需要全局搜索。

假设现在求最大值问题，那么：

一个较大的惯性权值有利于全局搜索，而一个较小的权值则更利于局部搜索。

假设现在一共五个粒子ABCDE，此时它们的适应度分别为1，2，3，4，5。取最大惯性权重为0.9，最小惯性权重为0.4 。那么，这五个粒子的惯性权重应该为：0.9，0.9，0.9，0.65，0.4。适应度越小，说明距离最优解越远，此时更需要全局搜索；适应度越大，说明距离最优解越近，此时更需要局部搜索。

3.随机惯性权重

最开始提出随机惯性权重的论文：Zhang L, Yu H, Hu S. A New Approach to Improve Particle Swarm Optimization[J]. lecture notes in computer science, 2003, 2723:134-139.

使用随机的惯性权重，可以避免在迭代前期局部搜索能力的不足；也可以避免在迭代后期全局搜索能力的不足。

后面有一个对随机惯性权重的改进。

参考文献：基于随机惯性权重的简化粒子群优化算法[J].计算机应用研究，2014, 031(002):361-363,391.

其中：μmin是随机惯性权重的最小值；μmax是随机惯性权重的最大值；rand()为[0, 1]均匀分布随机数；第三项中randn()为正态分布的随机数；σ(标准差)用来度量随机变量权重w与其数学期望（即均值）之间的偏离程度，该项是为了控制取值中的权重误差，使权重w有利于向期望权重方向进化，这样做的依据是正常情况下实验误差服从正态分布。

一般σ取0.2-0.5之间的一个数。

4.压缩因子法

个体学习因子c1和社会（群体）学习因子c2决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响，其反映了粒子群之间的信息交流。设置c1较大的值，会使粒子过多地在自身的局部范围内搜索，而较大的c2的值，则又会促使粒子过早收敛到局部最优值。

为了有效地控制粒子的飞行速度，使算法达到全局搜索与局部搜索两者间的有效平衡，Clerc构造了引入收缩因子的PSO模型，采用了压缩因子，这种调整方法通过合适选取参数，可确保PS0算法的收敛性，并可取消对速度的边界限制。

参考文献：M. Clerc. The swarm and queen: towards a deterministic and adaptive particle swarm op-timization. Proc. Congress on Evolutionary Computation, Washington, DC,.Piscataway,NJ:IEEE Service Center (1999) 1951- 1957

压缩因子法中应用较多的个体学习因子c1和社会学习因子c2均取2.05，用我们自己的符号可以表示为：

惯性权重w = 0.9，速度更新公式为：

将c1r1看成c1即可，c2r2看成c2即可。

参考文献：Eberhart R C. Comparing inertia weights and constriction factors in optimization[C]// Proceedings of the 2000 IEEE Congress on Evolutionary Computation, La Jolla, CA. IEEE, 2000.

5.非对称学习因子法

在经典PSO算法中，由于在手优后期粒子缺之多样性，易过早收敛于局部极值，因此通过调节学习因子，在搜索初期使粒子进行大范围搜索，以期获得具有更好多样性的高质量粒子，尽可能摆脱局部极值的干扰。

学习因子c1和c2决定粒子个体经验信息和其他粒子经验信息对寻优轨迹的影响，反映了粒子之间的信息交换。设置较大的c1值，会使粒子过多的在局部搜索（这里的局部搜索指的是粒子会过多的在自身的局部范围内进行搜索，从全局来看实际上增大了搜索范围。可以想象成每个粒子各干各的事情，团队意识比较弱）；反之，较大的c2值会使粒子过早收敛到局部最优值。因此，在算法搜索初期采用较大的c1值和较小的c2值，使粒子尽量发散到搜索空间即强调“个体独立意识”，而较少受到种群内其他粒子即“社会意识部分”的影响，以增加群内粒子的多样性。随着迭代次数的增加，使c1线性递减，c2线性递增，从而加强了粒子向全局最优点的收敛能力：

c1 = c1i + k × (c1f - c1i) / kmax

c2 = c2i + k × (c2f - c2i) / kmax

其中，k为当前迭代次数；kmax是最大迭代数；c1i、c2i分别为c1、c2的初始值；c1f、c2f分别为c1、c2的最终值。

根据上述收敛性分析，在迭代过程中w值从1线性递减到0.4,参数c1和c2在满足c = c1 + c2 ≤ 4的条件下，有3种取值情况：

1. c1和c2是常数且c1 = c2。表示“个体”与“群体”对粒子搜索过程的影响力相同
2. c1和c2是对称的线性变化关系。即c1i = c2f且c2i = c1f，表示“个体”与“群体”对搜索过程起完全互补的作用，这是经典PSO的思想
3. c1和c2是非对称的线性变化关系。即c1i ≠ c2f且c2i ≠ c1f，表示“个体”与“群体”对搜索过程具有不同程度的影响，这也是本文的改进PSO算法

综合以上分析，基于c1 = 2.5-0.5，c2 = 1.0-2.25 的非对称学习因子调节策略与文献[5]的对称调节以及学习因子固定取值的方法相比，均有较为明显的改善，表现出较好的全局寻优能力。

参考文献：毛开富,包广清,徐驰.基于非对称学习因子调节的粒子群优化算法[J].计算机工程，2010(19):188-190.

按照我们的符号就是：