黑客灵魂

这个屌丝很懒，什么也没留下！

热门标签

深度学习卷积神经网络参数计算难点重点_卷积层降维的困难

作者：黑客灵魂 | 2024-07-04 14:34:54

踩

卷积层降维的困难

一、卷积层图像输出尺寸

二、池化层图像输出尺寸

三、全连接层输出尺寸

四、卷积层参数数量

五、全连接层参数数量

六、代码实现与验证

以LeNet5经典模型为例子并且通道数为1

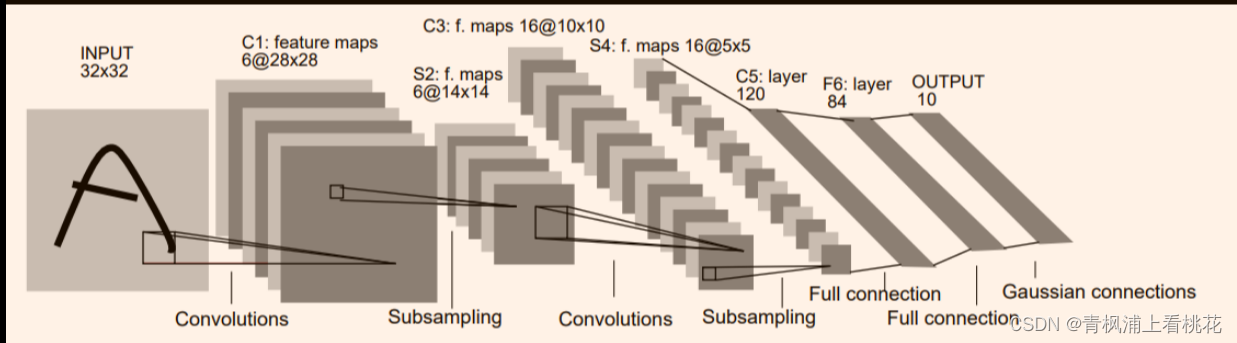
LeNet5网络有7层：

1.第1层：卷积层

输入：原始的图片像素矩阵（长度、宽度、通道数），大小为32×32×1；

参数：滤波器尺寸为5×5，深度为6，不使用全0填充，步长为1；

输出：特征图，大小为28×28×6。

分析：因为没有使用全0填充，所以输出尺寸 = 32 - 5 + 1 = 28，深度与滤波器深度一致，为6。

2.第2层：池化层

输入：特征图，大小为28×28×6；

参数：滤波器尺寸为2×2，步长为2；

输出：特征图，大小为14×14×6。

3.第3层：卷积层

输入：特征图，大小为14×14×6；

参数：滤波器尺寸为5×5，深度为16，不使用全0填充，步长为1；

输出：特征图，大小为10×10×16。

分析：因为没有使用全0填充，所以输出尺寸 = 14 - 5 + 1 = 10，深度与滤波器深度一致，为16。

4.第4层：池化层

输入：特征图，大小为10×10×16；

参数：滤波器尺寸为2×2，步长为2；

输出：特征图，大小为5×5×16。

5.第5层：全连接层

输入节点个数：5×5×16 = 400；

参数个数：5×5×16×120+120 = 48120；

输出节点个数：120。

6.第6层：全连接层

输入节点个数：120；

参数个数：120×84+84 = 10164；

输出节点个数：84。

7.第7层：全连接层

输入节点个数：84；

参数个数：84×10+10 = 850；

输出节点个数：10。

由于使用的是MNIST数据集，图片大小是28×28×1的，1代表通道数，也就是灰度图像，所以后面代码实现是用28×28的并进行讲解。

上面没看懂没关系，公式来了。

一、卷积层图像输出尺寸

定义如下：

O = 输出图像的尺寸。

I = 输入图像的尺寸。

K = 卷积层的核尺寸

N = 核数量

S = 移动步长

P = 填充数

公式：

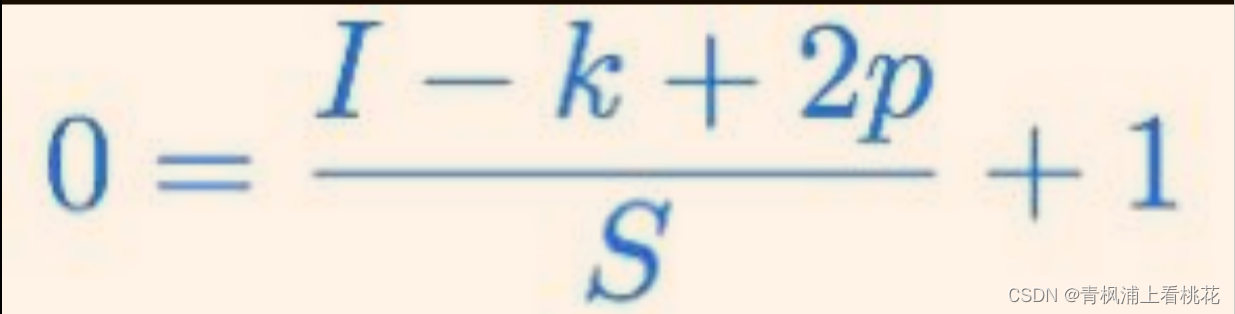
(数字0和字母O很像，请忽略掉这个小小问题)

示例：MNIST手写数字图片大小是28×28×1的，LeNet5第一层卷积核个数为5，故输出图像尺寸为：

故输出的图像大小为：24×24×6. （一个卷积核对应一个通道）

二、池化层图像输出尺寸

定义如下：

O=输出图像的尺寸。

I=输入图像的尺寸。

S=移动步长

PS=池化层尺寸

公式：

示例：第一层的输出为24×24×6，故输出图像尺寸为：

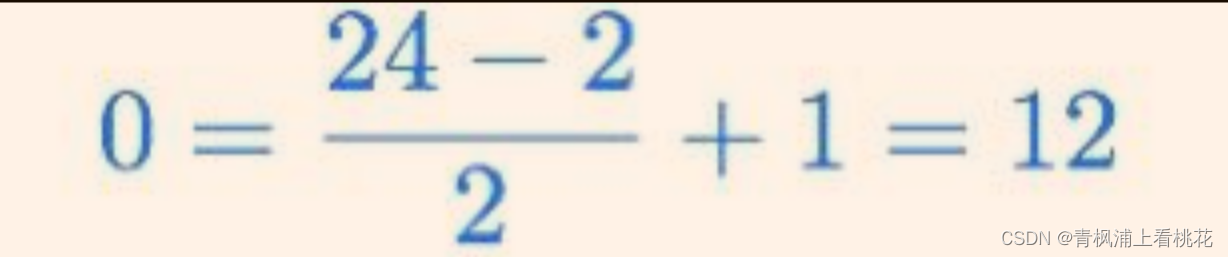
故输出的图像大小为：12×12×6. （池化层不改变通道个数）

三、全连接层输出尺寸

全连接层输出向量长度等于神经元的数量。

四、卷积层参数数量

在CNN中,每层有两种类型的参数:权重weights 和偏置项biases.总参数数量为所有weights和biases的总和.

定义如下:

WC = 卷积层的weights数量

BC = 卷积层的biases数量

PC = 所有参数的数量

K = 核尺寸

N = 核数量

C = 输入图像通道数

卷积层中,核的深度等于输入图像的通道数.于是每个核有K*K个参数.并且有N个核.由此得出以下的公式：

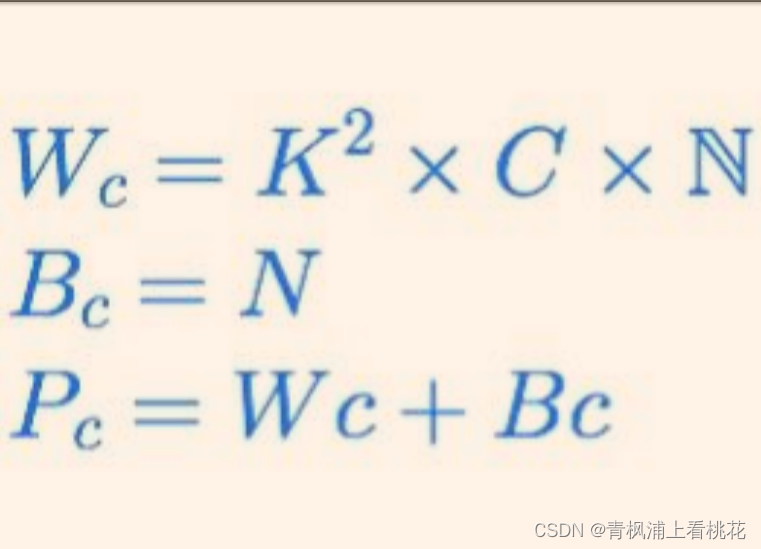
示例：LeNet5第一层卷积层，卷积核大小为5*5，并且有6个，输入图像大小为28×28×1，即K = 5, C = 1, N = 6，故有：

所以第一层的总参数量为：156。

池化层不计算参数。

五、全连接层参数数量

在CNN中有两种类型的全连接层。第1种是连接到最后1个卷积层,另外1种的FC层是连接到其他的FC层。两种情况分开讨论。

①连接到最后一个卷积层：

定义如下:

Wcf= weights的数量

Bcf= biases的数量

O= 前卷积层的输出图像的尺寸

N = 前卷积层的核数量

F = 全连接层的神经元数量

公式：

示例：以MNIST的28×28×1的输入图片为例，在LeNet5的第一个全连接层中，前面一层的输出图像大小为：4×4×16，该全连接层有120个神经元，即 O = 4, N = 16 , F = 120，故有：

所以该层总共有30840个参数。

②连接到上一个全连接层：

定义如下:

Wff= weights的数量

Bff= biases的数量

Pff= 总参数的数量

F= 当前FC层的神经元数量

F-1 = 前FC层的神经元数量

公式：

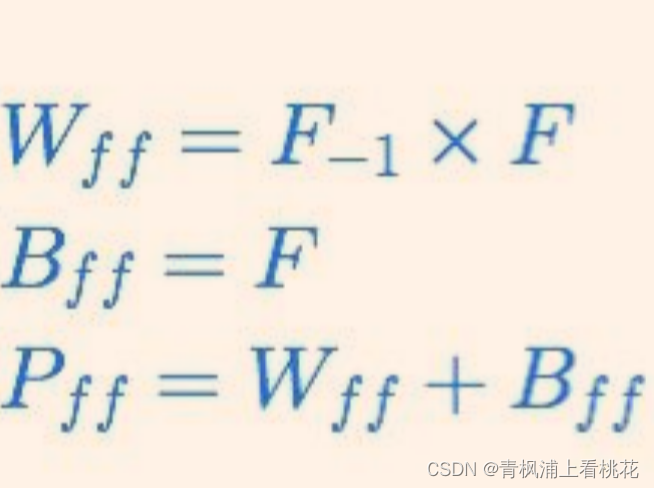
示例：LeNet5中全连接层的第2层，前一个全连接层的神经元个数为F-1 = 120, 当前层的神经元个数为F = 84，则有：

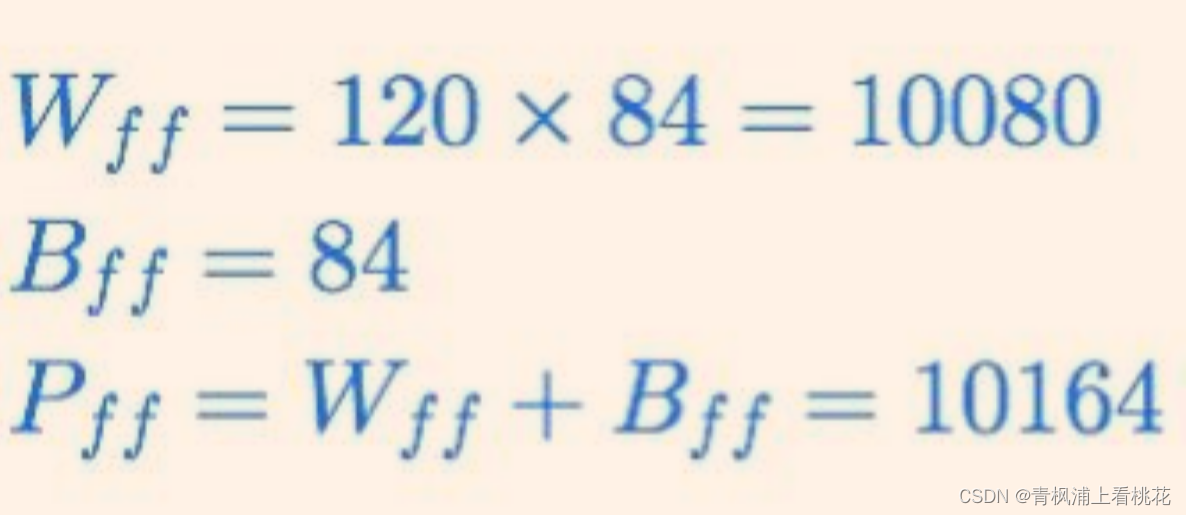
六、代码实现与验证

基于TensorFlow的代码实现如下：


# LeNet5网络模型
model = tf.keras.Sequential([
    # 第1层-卷积层 滤波器尺寸5*5,6个
    keras.layers.Conv2D(6,5),
    # 第2层-池化层,滤波器尺寸为2×2，步长为2
    keras.layers.MaxPooling2D(pool_size=2,strides=2),
    keras.layers.ReLU(),
    # 第3层-卷积层 滤波器尺寸5*5,16个
    keras.layers.Conv2D(16,5),
    # 第4层-池化层,滤波器尺寸为2×2，步长为2
    keras.layers.MaxPooling2D(pool_size=2,strides=2),
    keras.layers.ReLU(),
    keras.layers.Flatten(), # 拉平之后方便做全连接
    # 第5层-全连接层
    keras.layers.Dense(120,activation='relu'),
    # 第6层-全连接层
    keras.layers.Dense(84,activation='relu'),
    # 第7层-全连接层
    keras.layers.Dense(10,activation='softmax') # 最后输出10类,0-9的数字
])

运行代码输出：

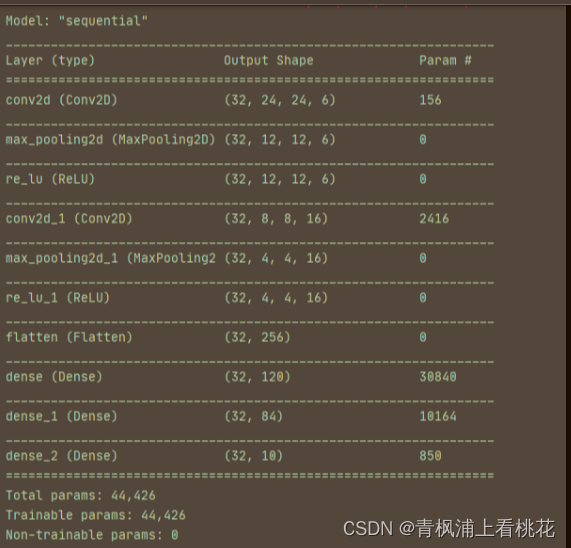
文献参考：

https://www.cnblogs.com/touch-skyer/p/9150039.html

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/黑客灵魂/article/detail/787238