排序（sort）_sort 排序

排序

1.概念

排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
平时的上下文中，如果提到排序，通常指的是排升序（非降序）。
通常意义上的排序，都是指的原地排序(in place sort)

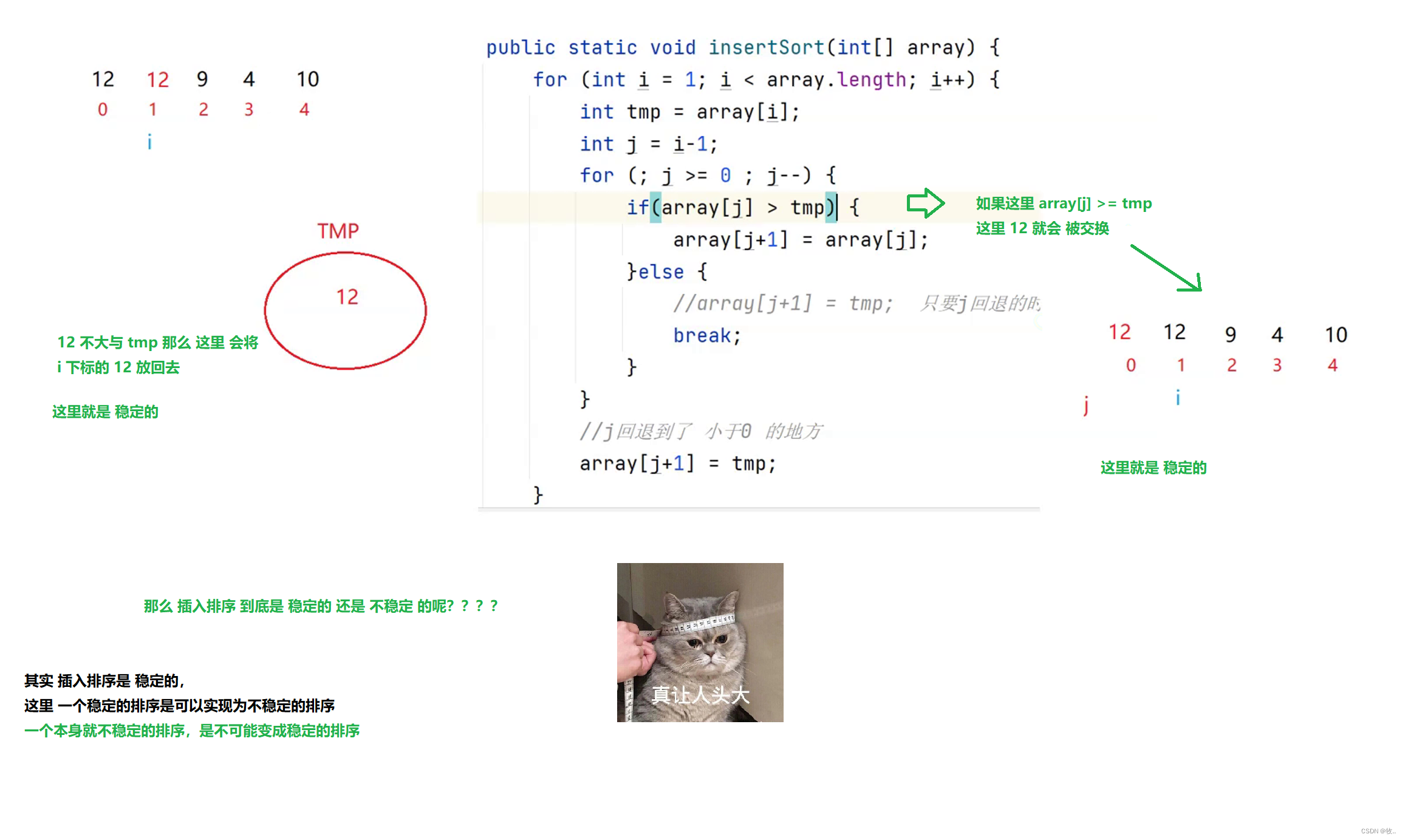
稳定性

两个相等的数据，如果经过排序后，排序算法能保证其相对位置不发生变化，则我们称该算法是具备稳定性的排序算
法。

1.插入排序

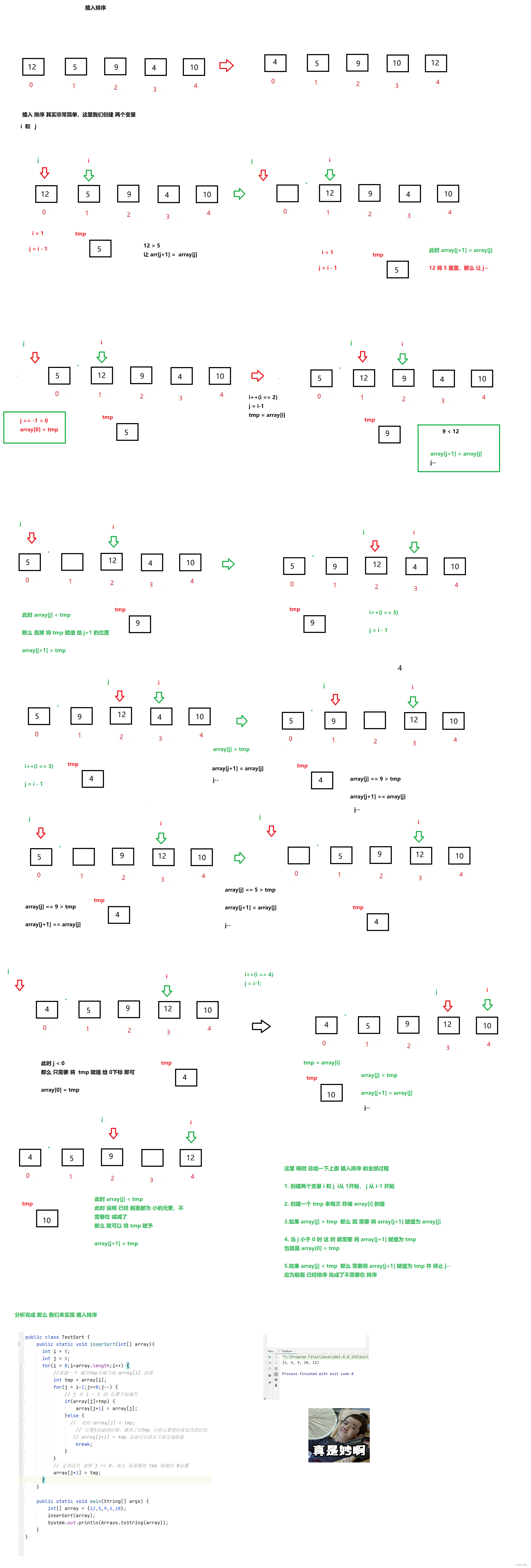
附上代码

 public static void inserSort(int[] array){
      int i = 0;
      int j = 0;
      for(i = 0;i<array.length;i++) {
          //创建一个 遍历tmp存储当前 array[i] 的值
          int tmp = array[i];
          for(j = i-1;j>=0;j--) {
              // j 从 i - 1 的 位置开始遍历
              if(array[j]>tmp) {
                  array[j+1] = array[j];
              }else {
                //  此时 array[j] < tmp;
                  // 只要j回退的时候，遇到了比tmp 小的元素就结束这次的比较
                 // array[j+1] = tmp 这就可以放在下面完成赋值
                  break;
              }
          }
          // 走到这里 说明 j == 0，那么 就需要将 tmp 赋值给 0位置
          array[j+1] = tmp;
      }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

接下来 我们继续

插入 排序 的 时间复杂度 为 O(N^2)

最好的情况下 时间复杂度 为 O(N) 这里数据 为 有序的情况下

如 1 2 3 4 5 这 就 j 就 不会 往 回 走 所以 时间 复杂度 为 O(N)

根据上面这个 可以 推出 对于直接插入排序来说，数据越有序，排序越快

空间 复杂度 为 O(1)

插入排序的稳定性 插入排序 是 稳定的

2.希尔排序

我们 刚刚 学习 了 插入 排序 ，那么 希尔排序是 在 插入排序的基础上优化而来。

回忆一下我们 我们 是不是 得出 插入排序的时间复杂度是O(N^2)

如果 是排序 有序的数据那么时间复杂度不就成为了O(N)了。

这里结论不就是 越有序，排序越快。

接下来 我们 代码实现 希尔排序

    public static void shell(int[] array,int gap) {
        int j = 0;
        for(int i = gap;i<array.length;i++) {
            int tmp = array[i];
            for(j = i - gap;j>=0;j = j-gap) {
                if(array[j] > tmp) {
                    array[j+gap] = array[j];
                }else {
                    break;
                }
            }
            array[j+gap] = tmp;
        }
    }
    public static void shellSort(int[] array) {
        int gap = array.length;
        while(gap > 1) {
            shell(array,gap);
            gap /= 2;
        }
        shell(array,1);// 保证最后一组数据是一
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

是不是 很像插入排序呀，别看上面分析了那么多 图 ，不过 只是在插入排序上 修改 了 一点东西而已。。

接下来我们 来看一看 希尔排序的 时间复杂度

希尔排序的 时间复杂度

3.选择排序

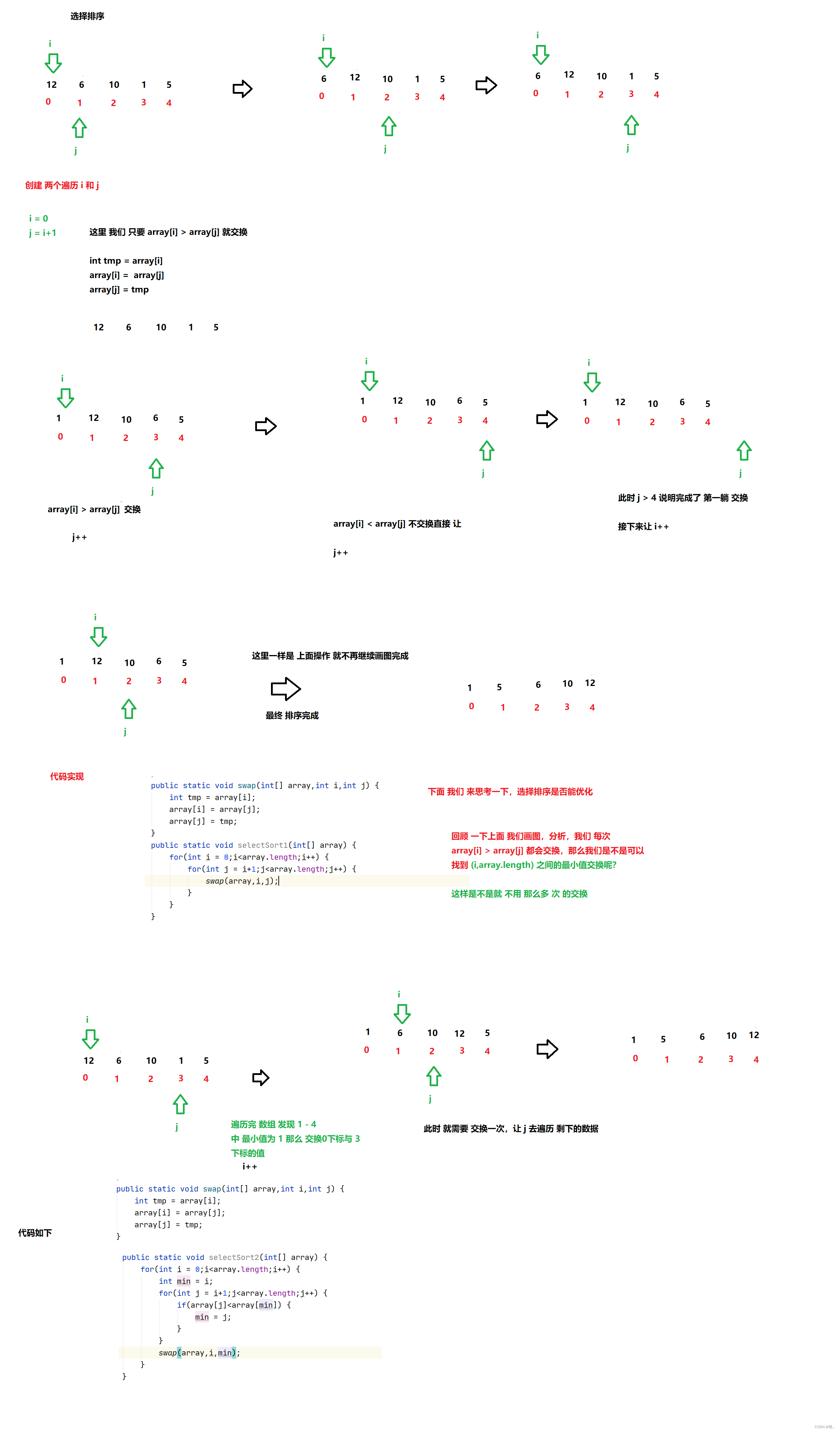
附上代码

   public static void swap(int[] array,int i,int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
    public static void selectSort1(int[] array) {
        for(int i = 0;i<array.length;i++) {
            for(int j = i+1;j<array.length;j++) {
                 if( array[j] < arr[i]){
                      swap(array,i,j);
                 }    
            }
        }
    }
    public static void selectSort2(int[] array) {
        for(int i = 0;i<array.length;i++) {
            int min = i;
            for(int j = i+1;j<array.length;j++) {
                if(array[j]<array[min]) {
                    min = j;
                }
            }
            swap(array,i,min);
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

这里不管是否优化，这里是时间复杂度 都为 O(N^2)

4.堆排序

堆排序 在 我 堆的 博客中就已经完成，这里就不在画图 推导，这里就直接附上代码

堆博客

附上代码

  /**
     * 堆排序
     */
    public  static void heapSort(int[] array) {
        createHeap(array);
        int end = array.length -1;
        while(end > 0) {
            swap(array,0,end);
            shifDown(array,0,end);
            end--;
        }
    }
    public static void shifDown(int[] array,int parent,int len) {
        int child = parent * 2 + 1;
        while(child < len) {
            if(child + 1 < len && array[child] < array[child+1]) {
                child++;
            }
            if(array[parent] < array[child]) {
                swap(array,parent,child);
                parent = child;
                child = 2 * parent + 1;
            }else {
                break;
            }
        }
    }
    public static void createHeap(int[] array) {
        for(int parent = (array.length - 1 - 1) / 2;parent>=0;parent--) {
            shifDown(array,parent,array.length);
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

5.冒泡排序

想必大家 应该 很熟悉冒泡排序吧，如果不熟悉，这里我们 还是 通过画图 来 让大家熟悉他。

附上代码

 public static void swap(int[] array,int i,int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }

public static void bubbleSort1(int[] array) {
        for(int i = 0;i<array.length-1;i++) {
            for(int j = 0;j<array.length-1-i;j++) {
                if(array[j] > array[j+1]) {
                    swap(array,j,j+1);
                }
            }
        }
    }
    
    // 优化
    public static void bubbleSort2(int[] array) {
        for(int i = 0;i<array.length-1;i++) {
            boolean flg = true;
            for(int j = 0;j<array.length-1-i;j++) {
                if(array[j] > array[j+1]) {
                    flg = false;
                    swap(array,j,j+1);
                }
            }
            if(flg) {
                break;
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

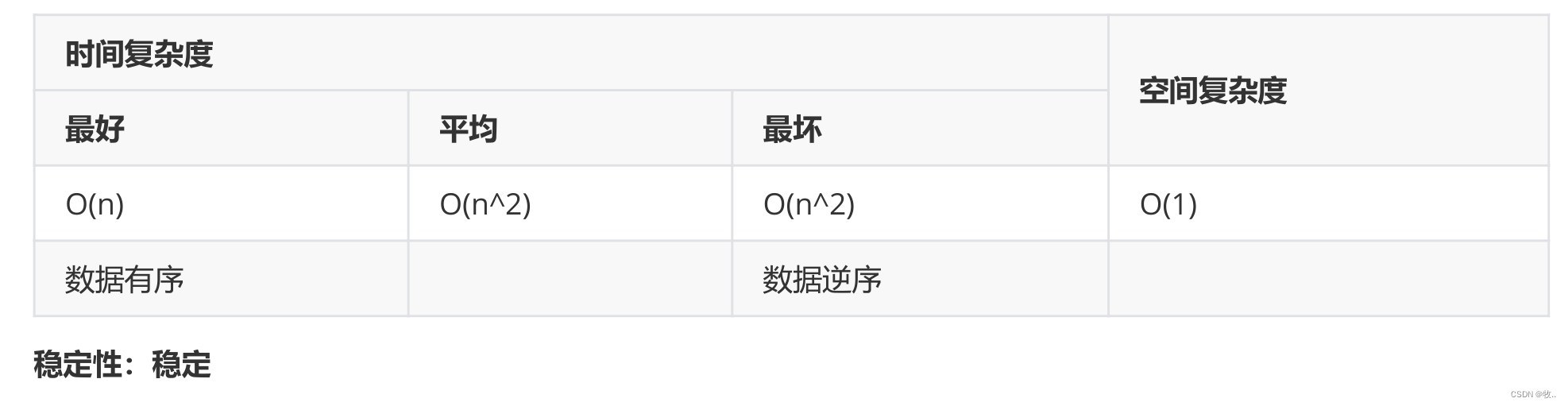
冒泡排序的时间复杂度 不管是好是坏 时间复杂度都是O(N^2) 。

空间 复杂度 为 O(1)

稳定 性 ： 冒泡排序是一个稳定的排序

这里 O(N) 其实就是给了 一个 有序的数组， 第二个 循环 if 语句 不会 进入 ，优化 后的 冒泡 排序 第一趟 后就会结束循环

6.快速排序

附上代码

   public static void quickSort(int[] array) {
        quick(array,0,array.length-1);
    }
    public static void quick(int[] array,int start,int end) {
        if(start >= end) {
            return;
        }
        // 这start 和 end  形参的值 改变了  而 我们 实参的 start 和 end 还是 指向 0 和 array.length -1
      int piovt  =  partition(array,start,end);
        quick(array,start,piovt - 1);
        quick(array,piovt+1,end);
    }
    // 找基准
    public static int partition(int[] array,int start,int end) {
        int tmp = array[start];
        while(start < end) {
            while(start < end && array[end] >= tmp) {
                end--;
            }
            //end 下标就遇到 < tmp 的值
            array[start] = array[end];
            while(start < end  && array[start] <= tmp) {
                start++;
            }
            //end 下标就遇到 > tmp 的值 
            array[end] = array[start];
        }
        array[start] = tmp;
        // 或 array[end] = tmp;
        return start;
        // return end;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

解下来我们 来 看一下 快速排序的 时间复杂度

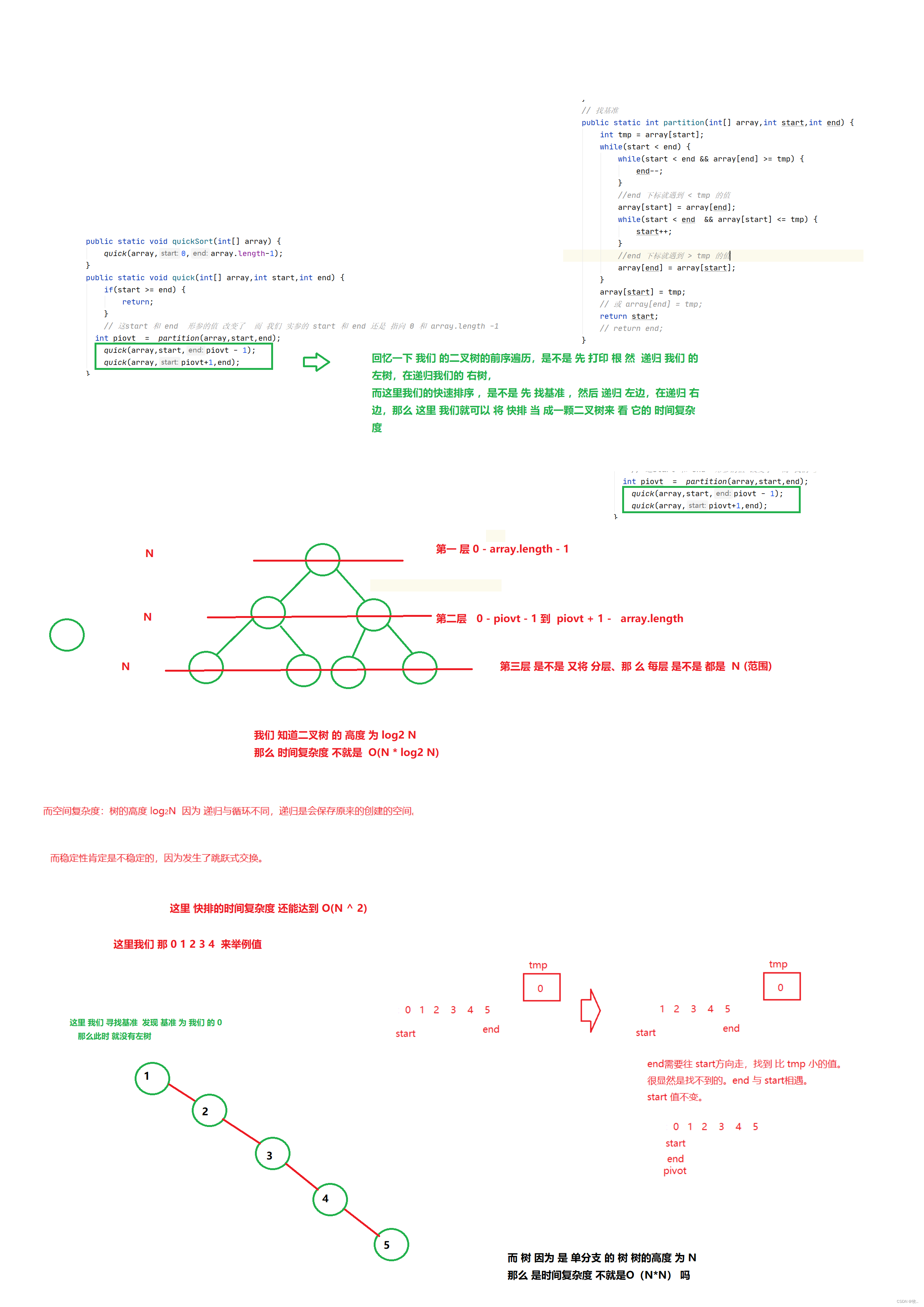
空间复杂度O(N)

稳定性 ，不稳定发生了跳跃性交换 。

堆排 与 快 排时间复杂度的区别

上面我们 提到了堆排的 时间复杂度 为O( N * log2 N) 而 快排也 是 O(N * log2 N) ,那么 为啥 快排 要 比 堆排 快呢？

堆排序，无论最好还是最坏情况，时间复杂度都是N log2 N。空间复杂度 O(1)*
快排 ， 时间复杂度 最好的情况下O(N * log2 N) 空间复杂度0(N),

其实这里 堆排和快排时间复杂度的连着前面还有 一个 k【K * N log2 N 】，*

只不过快排前面的K要小一点。所以快排要快一点。

两者的使用

在对空间复杂度没有要求的情况： 使用快排
对空间复杂度有要求的情况，或者说对数据的序列也要要求： 堆排

快排的小细节

Hoare 法:完成快排

其实 hoare法 与 挖坑法 很像这里我们 挖坑法找到 了 合适 的值，赋值留下一个坑 ，而 hoare array[start] 找到 大于基准的值 停下，然后，找array[end]小于基准的值，找到了停下，完成交换。然后继续重复上面操作

附上代码

private static int partition(int[] array, int left, int right) {
    int start = left;
    int end = right;
    int pivot = array[left];
    while (start < end) {
    while (start < end && array[end] >= pivot) {
   			 end--;
    }
    while (start < end && array[start] <= pivot) {
   			 start++;
    	}
        swap(array, start, end);
	}
    // 此时 start 与 end 相遇
        swap(array, start, left);
        return i;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

快排优化

上面我们是不是 通过 递归 来完成了 快排，每次递归 我们都需要开辟一个栈帧 ，如果 元素 又几百万上千万，那么大家想一想我们的栈是不是会被挤爆，从而报错，接下来我们就来优化我们的快排，让他不那么因为太多数据而出现栈溢出的现象。

基准值的选择

在优化前我们 先来 基准值的选择

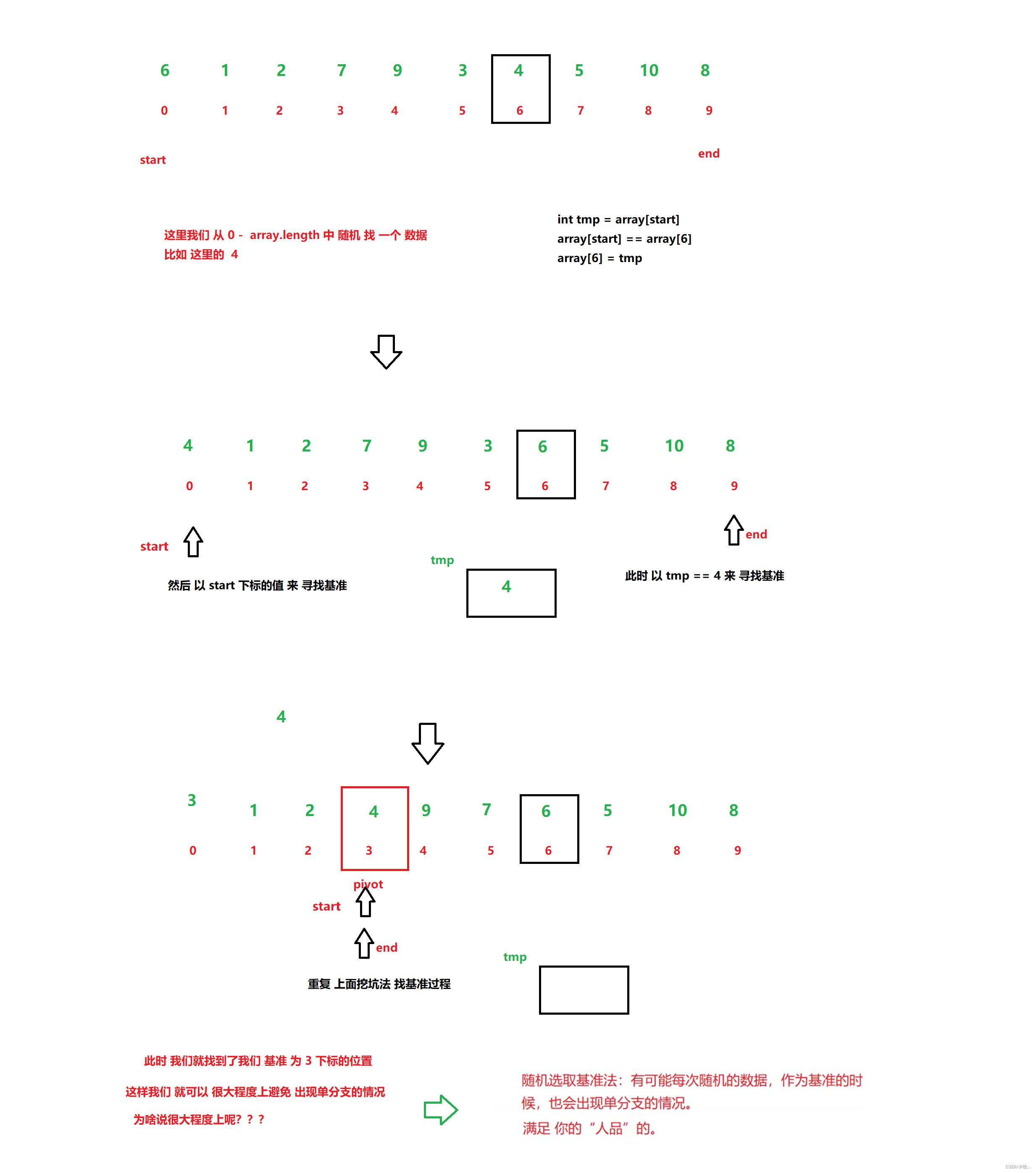
1.选择边上（左或者右）

选择边上这里我们是不是就是挖坑法 或 Hoare 的 方法，通过边上来找基准，

但这种 基准选择可能出先单分支的情况，导致时间复杂度为O(N^2) 如 0 1 2 3 4 5

2.随机选择

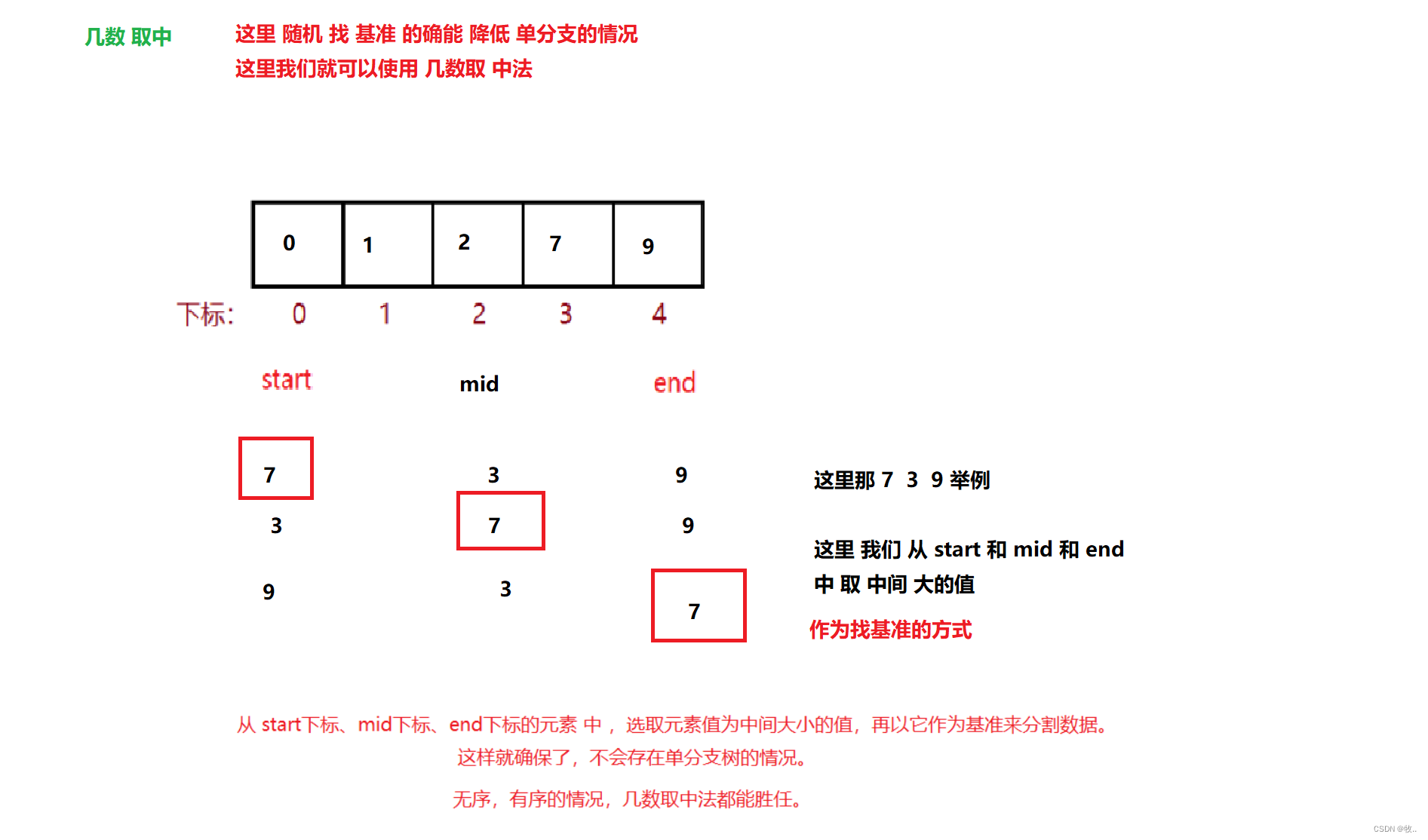
3几数取中（例如三数取中）：array[left], array[mid], array[right] 大小是中间的为基准值

附上代码

   public static void quickSort(int[] array) {
        quick(array,0,array.length-1);
    }
    public static void quick(int[] array,int start,int end) {
        if(start >= end) {
            return;
        }
        // 找基准之前，我们找到中间大小的值 - 使用三数取中法
        int midValIndex = findmidValIndex(array,start,end);
        //交换 0 下标 与 中间值 
        swap(array,start,midValIndex);
      int piovt  =  partition(array,start,end);
        quick(array,start,piovt - 1);
        quick(array,piovt+1,end);
    }
    public static int findmidValIndex (int[] array,int start,int end) {
        int mid = start + ((end - start) >>>1);
        // 注意 + 的 优先级 大于 >>> 这里就等价于 （start+ end）/ 2
        if(array[start] < array[end]) {
            if(array[mid] < array[start]) {
                return start;
            }else if(array[mid] > array[end]){
                return end;
            }else {
                return mid;
            }
        }else {
            if(array[mid] > array[start]) {
                return start;
            }else if(array[mid] < array[end]) {
                return end;
            }else {
                return mid;
            }
        }
    }
    // 找基准
    public static int partition(int[] array,int start,int end) {
        int tmp = array[start];
        while(start < end) {
            while(start < end && array[end] >= tmp) {
                end--;
            }
            //end 下标就遇到 < tmp 的值
            array[start] = array[end];
            while(start < end  && array[start] <= tmp) {
                start++;
            }
            //end 下标就遇到 > tmp 的值
            array[end] = array[start];
        }
        array[start] = tmp;
        // 或 array[end] = tmp;
        return start;
        // return end;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

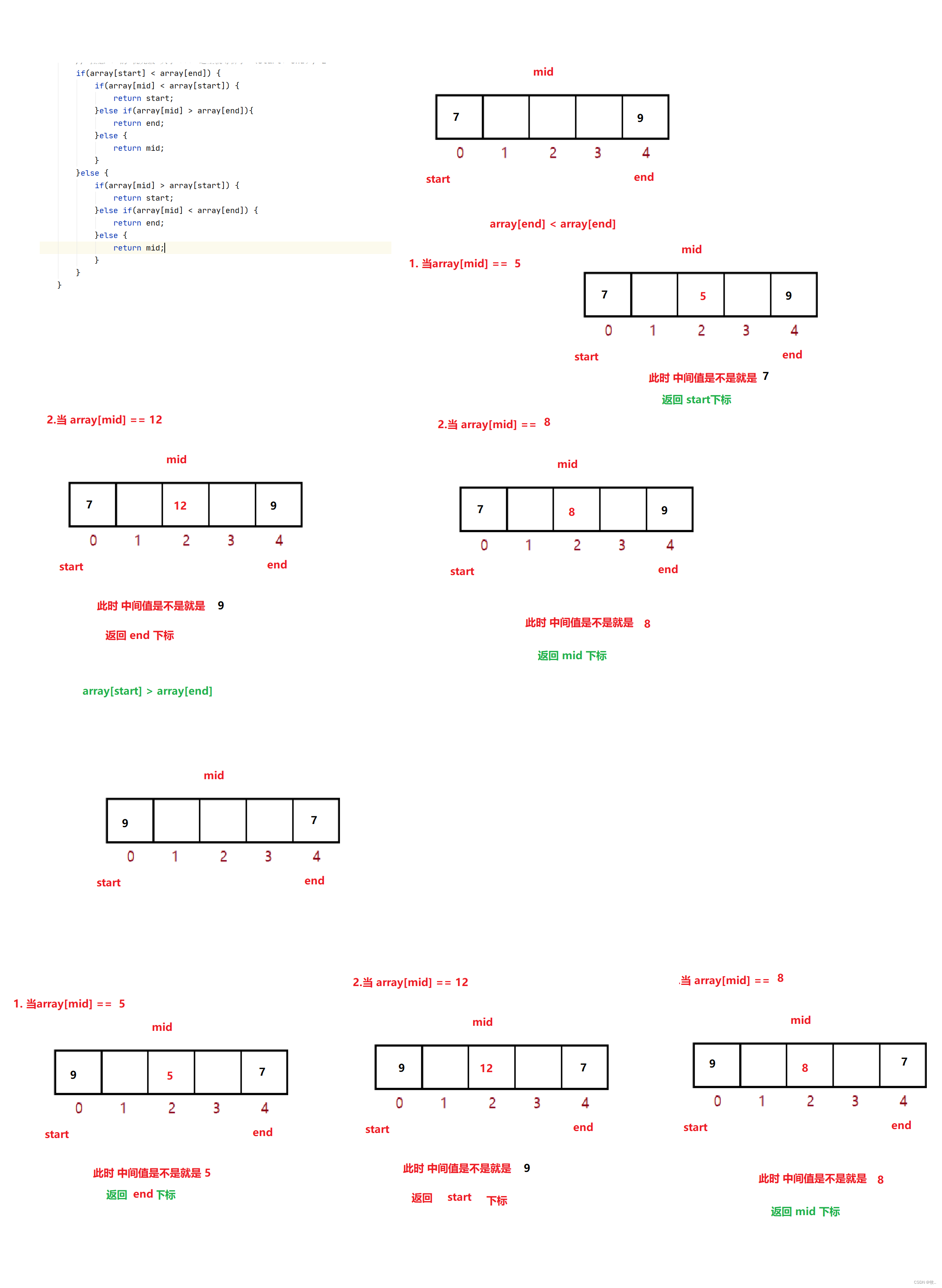
此时 我们 如果 使用 现在的 代码 取 递归 很大的数 就 不会 出现 栈溢出，但是 如果 数字 非常非常大还是 会出现的，因为 递归的程度 过深。

优化总结

1. 选择基准值很重要，通常使用几数取中法

2. partition 过程中把和基准值相等的数也选择出来

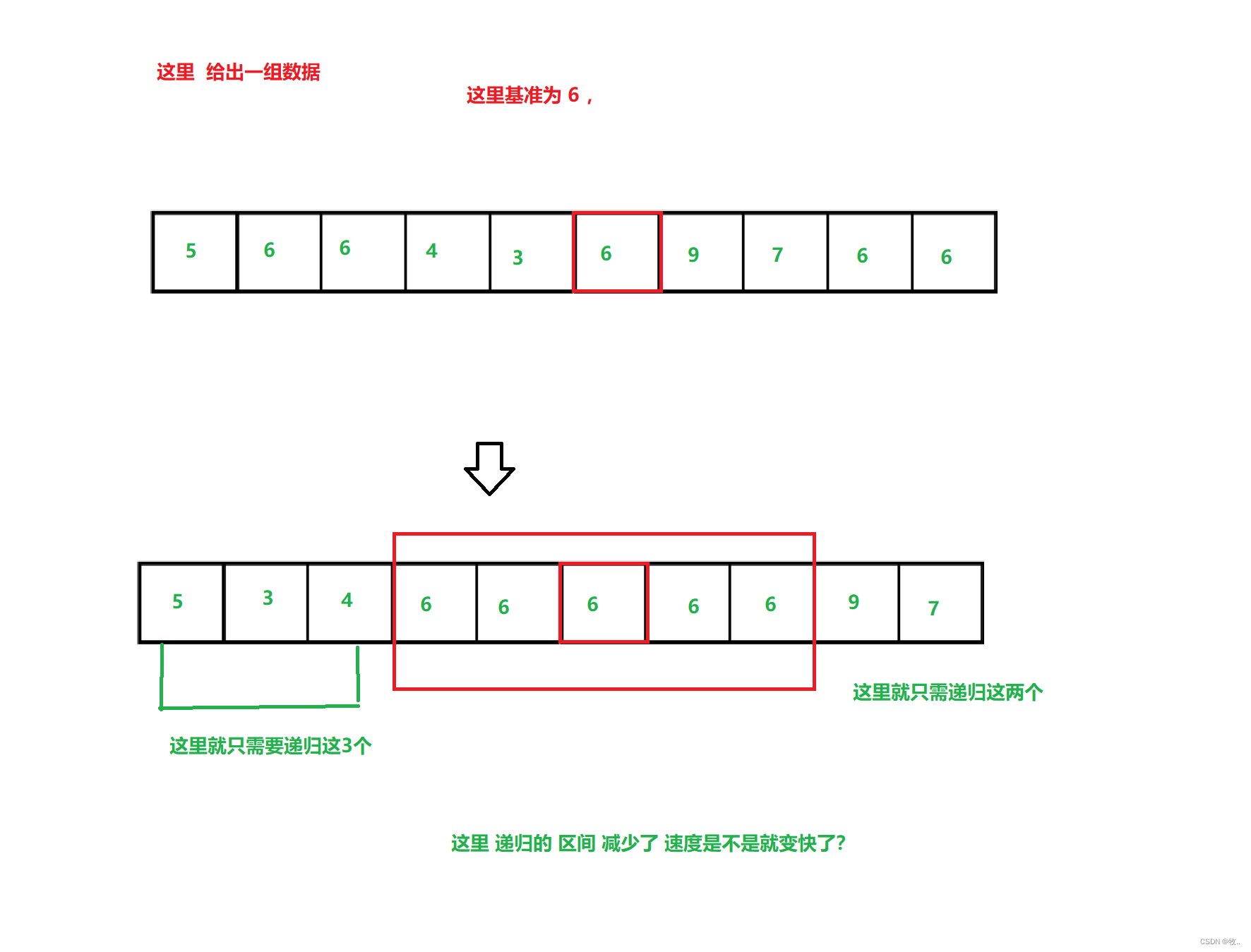
3. 待排序区间小于一个阈值时（例如 148），使用直接插入排序

上面我们 总结 过 直接插入排序的一个性质，是不是 数据 越有序 排序 的 越快，那么我们就可以 通过 这个性质来优化快排，我们 给定一个 阀值，

如果 区间（right - left +1） 等于了 阈值那么调用直接插入排序，来排序数据，这样就完成了我们的优化。

附上代码

  直接插入排序
  
  public static void inserSort(int[] array) {
       int i = 0;
       int j = 0;
       for(i = 1;i<array.length;i++) {
           int tmp = array[i];
           for(j = i - 1;j<array.length;j++) {
               if(array[j] > tmp) {
                   array[j+1] = array[j];
               }else {
                   break;
               }
               array[j+1] = tmp;
           }
       }
    }
  public static void quickSort(int[] array) {
        quick(array,0,array.length-1);
    }
    public static void quick(int[] array,int start,int end) {
        if(start >= end) {
            return;
        }

        // 通过 直接插入排序优化
        if(end - start + 1 == 148) {
            inserSort(array);
            return;
        }
        // 找基准之前，我们找到中间大小的值 - 使用三数取中法
        int midValIndex = findmidValIndex(array,start,end);
        swap(array,start,midValIndex);
        
       int piovt  =  partition(array,start,end);
        //这里 只能找到 pivot 前面等于 piovt 的值
        quick(array,start,piovt - 1);
        quick(array,piovt+1,end);
    }
    public static int findmidValIndex (int[] array,int start,int end) {
        int mid = start + ((end - start) >>>1);
        // 注意 + 的 优先级 大于 >>> 这里就等价于 （start+ end）/ 2
        if(array[start] < array[end]) {
            if(array[mid] < array[start]) {
                return start;
            }else if(array[mid] > array[end]){
                return end;
            }else {
                return mid;
            }
        }else {
            if(array[mid] > array[start]) {
                return start;
            }else if(array[mid] < array[end]) {
                return end;
            }else {
                return mid;
            }
        }
    }
    // 找基准
    public static int partition(int[] array,int start,int end) {
        int tmp = array[start];
        while(start < end) {
            while(start < end && array[end] >= tmp) {
                end--;
            }
            //end 下标就遇到 < tmp 的值
            array[start] = array[end];
            while(start < end  && array[start] <= tmp) {
                start++;
            }
            //end 下标就遇到 > tmp 的值
            array[end] = array[start];
        }
        array[start] = tmp;
        // 或 array[end] = tmp;
        return start;
        // return end;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

快速排序非递归实现

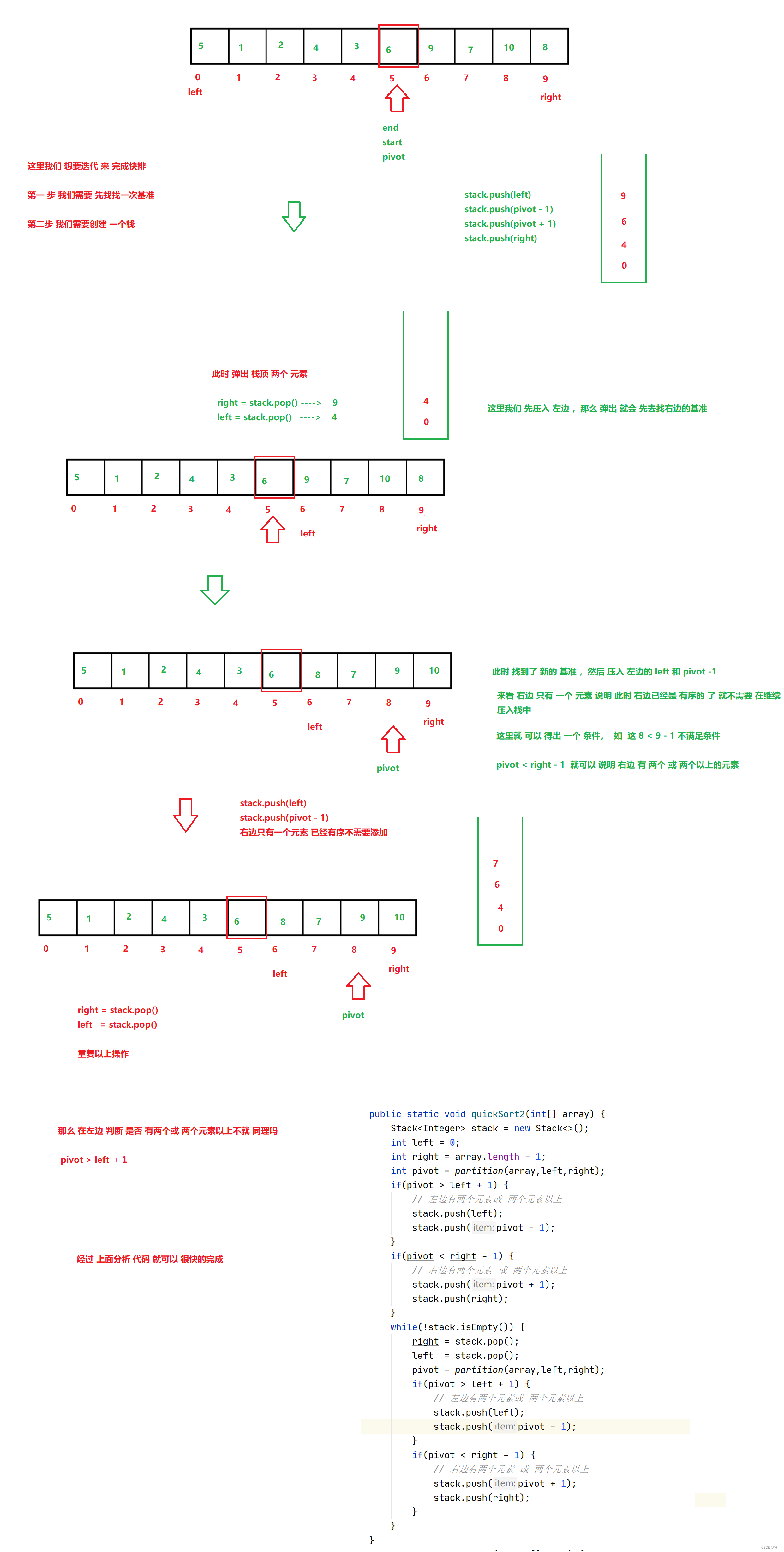
附上代码

   public static void quickSort2(int[] array) {
        Stack<Integer> stack = new Stack<>();
        int left = 0;
        int right = array.length - 1;
        int pivot = partition(array,left,right);
        if(pivot > left + 1) {
            // 左边有两个元素或 两个元素以上
            stack.push(left);
            stack.push(pivot - 1);
        }
        if(pivot < right - 1) {
            // 右边有两个元素 或 两个元素以上
            stack.push(pivot + 1);
            stack.push(right);
        }
        while(!stack.isEmpty()) {
            right = stack.pop();
            left  = stack.pop();
            pivot = partition(array,left,right);
            if(pivot > left + 1) {
                // 左边有两个元素或 两个元素以上
                stack.push(left);
                stack.push(pivot - 1);
            }
            if(pivot < right - 1) {
                // 右边有两个元素 或 两个元素以上
                stack.push(pivot + 1);
                stack.push(right);
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

7.归并排序

预备 练习

给你两个有序的数组 合并 成一个有序 的 数组

附上代码

    public static int[] mergeArray2(int[] arr1, int[] arr2) {
        if(arr1 == null && arr2 != null) {
            return arr2;
        }
        if(arr1 != null && arr2 == null) {
            return arr1;
        }
        if(arr1 == null && arr2 == null) {
            return null;
        }
        int count = 0;
        int[] ret = new int[arr1.length + arr2.length];
        int s1 = 0;
        int e1 = arr1.length-1;
        int s2 = 0;
        int e2 = arr2.length-1;
        while(s1 <= e1 && s2 <= e2) {
            if(arr1[s1] <= arr2[s2]) {
                ret[count] = arr1[s1];
                count++;
                s1++;
            }else {
                ret[count] = arr2[s2];
                count++;
                s2++;
            }
        }
        // 此时说明 有一个数组 拷贝完成
        while(s1 <= e1) {
            ret[count] = arr1[s1];
            count++;
            s1++;
        }
        while(s2 <= e2) {
            ret[count] = arr2[s2];
            count++;
            s2++;
        }
        return ret;
    }
其实 也可以这样写
  public static int[] mergeArray(int[] arr1, int[] arr2) {
        if(arr1 == null && arr2 != null) {
            return arr2;
        }
        if(arr1 != null && arr2 == null) {
            return arr1;
        }
        if(arr1 == null && arr2 == null) {
            return null;
        }
        int[] ret = new int[arr1.length + arr2.length];
       int s1 = 0;
       int e1 = arr1.length-1;
       int s2 = 0;
       int e2 = arr2.length-1;
       int count = ret.length;
       int i = 0;
        while(i < count) {
            if(s1 <= e1 && s2 <= e2 && arr1[s1] <= arr2[s2]) {
                ret[i] = arr1[s1];
                i++;
                s1++;
            }else if(s1 <= e1 && s2 <=  e2 && arr1[s1] >= arr2[s2]){
                ret[i] = arr2[s2];
                i++;
                s2++;
            }
           while(s1 > e1 && s2  <= e2) {
               ret[i] = arr2[s2];
               i++;
               s2++;
           }
           while(s1 <= e1 && s2 >  e2) {
               ret[i] = arr1[s1];
               i++;
               s1++;
           }
        }
        return ret;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

完成了上面的预备练习，接下来学习我们的归并排序

附上代码

   /**
     * 归并排序
     */
    public static void mergeSort(int[] array) {
        mergeSortInternal(array,0,array.length - 1);
    }
    private static void mergeSortInternal(int[] array,int low,int high) {
        if(low >= high) {
            return;
        }
       // int mid = (low + high) >>> 2;
        int mid = low + ((high - low) >>> 1);
        // 递归 左边
        mergeSortInternal(array,low,mid);
        // 递归 右边
        mergeSortInternal(array,mid+1,high);
        // 归并
        merge(array,low,mid,high);

    }
    //回忆一下刚刚 写的 合并两个有序的，那么这里合并不就非常简单吗？
    private static void merge(int[] array,int low,int mid ,int high) {
        // 临时数组大小
        int[] ret = new int[high - low + 1];
        int s1 = low;
        int e1 = mid;
        int s2 = mid + 1;
        int e2 = high;
        int count = 0;
        // 注意 这里 是 同一个数组
        while(s1 <= e1 && s2 <= e2) {
            if(array[s1] <= array[s2]) {
                ret[count] = array[s1];
                count++;
                s1++;
            }else {
                ret[count] = array[s2];
                count++;
                s2++;
            }
        }
        // 此时说明 有一个数组 拷贝完成
        while(s1 <= e1) {
            ret[count] = array[s1];
            count++;
            s1++;
        }
        while(s2 <= e2) {
            ret[count] = array[s2];
            count++;
            s2++;
        }

        // 拷贝tmp 数组的元素 放入原来的数组array当中
            for(int i = 0;i<count;i++) {
                // 这里我们 每次加上归并区间的开始，就可 正好完成和并后的拷贝
                array[i+low] = ret[i];
            }
        }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

归并的时间复杂度 ： 这里我们 每一层都需要递归，那么树的高度为 O（log2 N） 每层 为N 那么时间复杂度 为O（N*log2 N）

归并的空间复杂度： O(N)

归并的稳定性 ： 稳定的排序

总结一下我们上面学习的排序，稳定的排序只有 冒泡 插入 归并

归并排序非递归实现

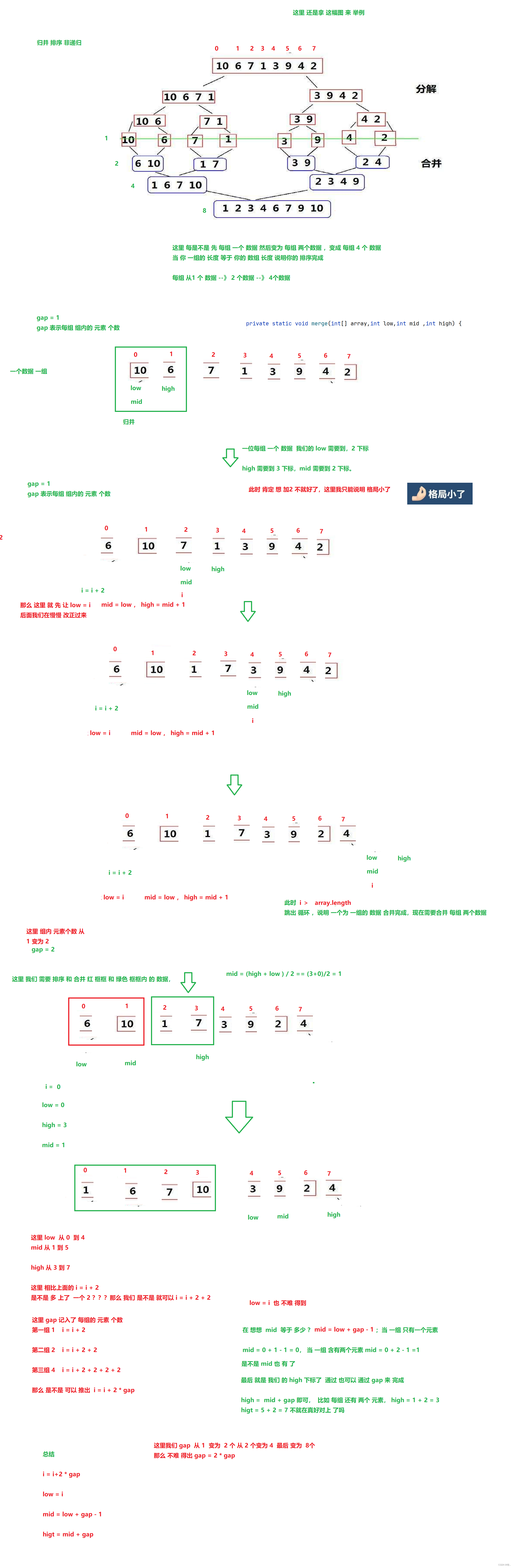
附上代码

   //回忆一下刚刚 写的 合并两个有序的，那么这里合并不就非常简单吗？                             
  private static void merge(int[] array,int low,int mid ,int high
      // 临时数组大小                                                  
      int[] ret = new int[high - low + 1];                       
      int s1 = low;                                              
      int e1 = mid;                                              
      int s2 = mid + 1;                                          
      int e2 = high;                                             
      int count = 0;                                             
      // 注意 这里 是 同一个数组                                           
      while(s1 <= e1 && s2 <= e2) {                              
          if(array[s1] <= array[s2]) {                           
              ret[count] = array[s1];                            
              count++;                                           
              s1++;                                              
          }else {                                                
              ret[count] = array[s2];                            
              count++;                                           
              s2++;                                              
          }                                                      
      }                                                          
      // 此时说明 有一个数组 拷贝完成                                         
      while(s1 <= e1) {                                          
          ret[count] = array[s1];                                
          count++;                                               
          s1++;                                                  
      }                                                          
      while(s2 <= e2) {                                          
          ret[count] = array[s2];                                
          count++;                                               
          s2++;                                                  
      }                                                          
                                                                 
      // 拷贝tmp 数组的元素 放入原来的数组array当中                              
          for(int i = 0;i<count;i++) {                           
              // 这里我们 每次加上归并区间的开始，就可 正好完成和并后的拷贝                  
              array[i+low] = ret[i];                             
          }                                                      
      }                                                          
                                                                 



  /**                                                           
   * 归并排序非递归实现                                                  
   */                                                           
  public static void mergeSort2(int[] array) {                  
      int nums = 1;// 每组的数据个数   nums  就看作 gap                                  
      while(nums < array.length) {  
          // 数组每次 都需要遍历
          for(int i = 0;i<array.length;i =  i + nums * 2) {     
              int low = i;                                     
              int mid = low + nums - 1;   
              // 这里 需要考虑 mid  和 high 可能 越界
              if(mid >= array.length) {                         
                  mid = array.length - 1;                       
                                                                
              }                                                 
              int high = mid + nums;                           
              if(high >= array.length - 1) {                   
                  high = array.length - 1;                     
              }                                                 
              // 下标确定后 进行 合并                                    
              merge(array,low,mid,high);                      
          }                                                     
          nums *= 2;                                            
      }                                                         
  }                                                             
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

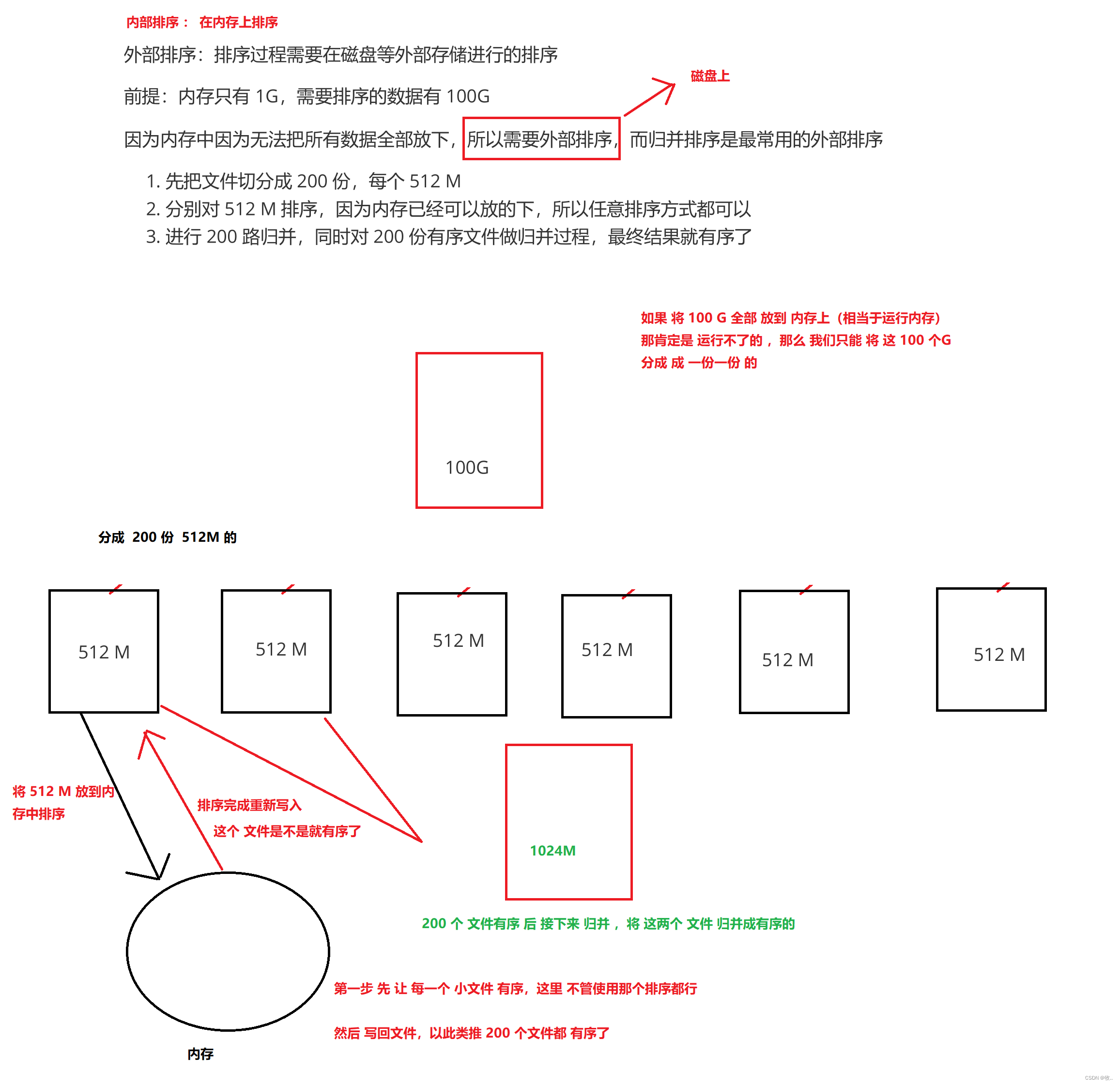
8.海量数据的排序问题

外部排序：排序过程需要在磁盘等外部存储进行的排序
前提：内存只有 1G，需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下，所以需要外部排序，而归并排序是最常用的外部排序

1. 先把文件切分成 200 份，每个 512 M

2. 分别对 512 M 排序，因为内存已经可以放的下，所以任意排序方式都可以

3. 进行 200 路归并，同时对 200 份有序文件做归并过程，最终结果就有序了
   

9.排序总结

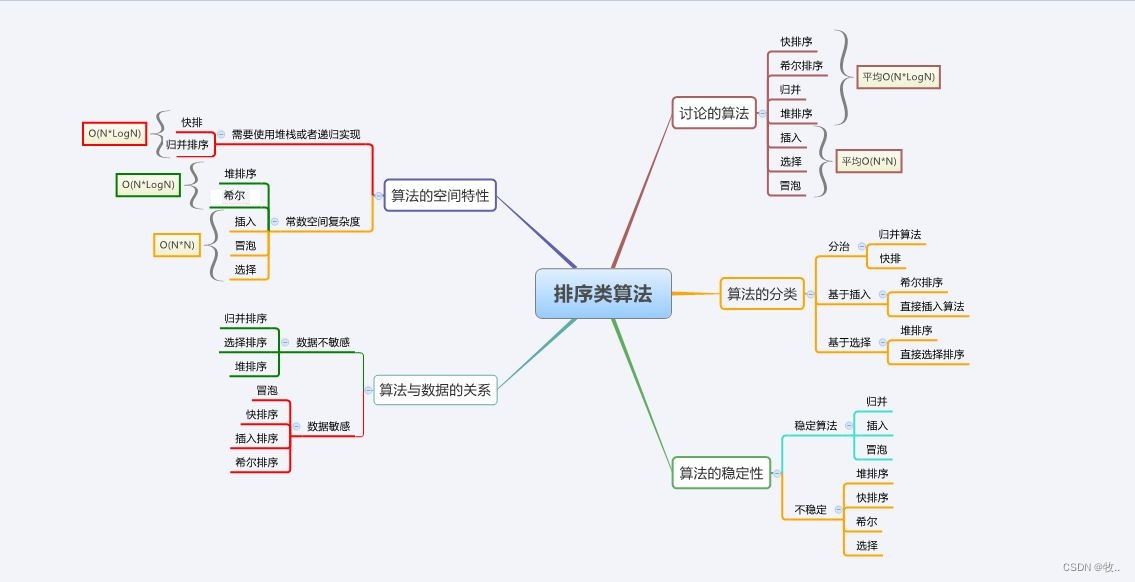
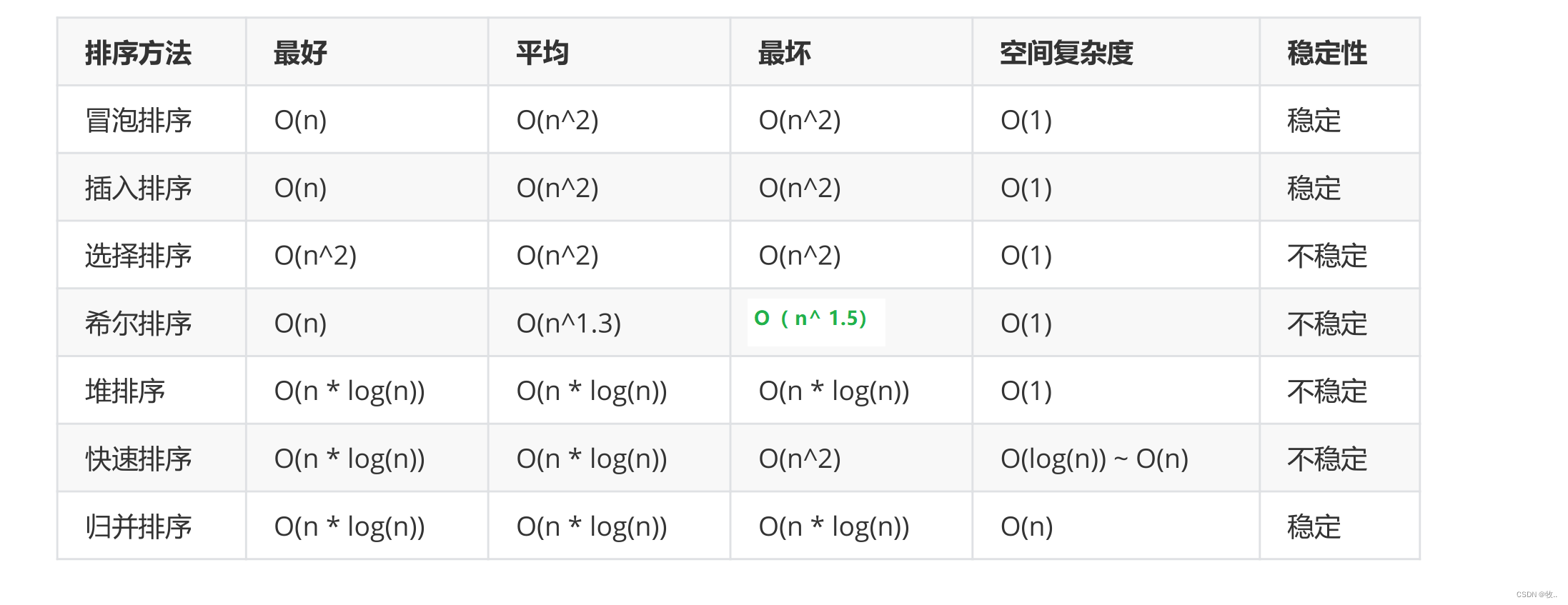
10.其他非基于比较的排序（了解即可）

不用比较大小将数据 变为有序的排序、

1.基数排序

[ 基数排序 | 菜鸟教程]

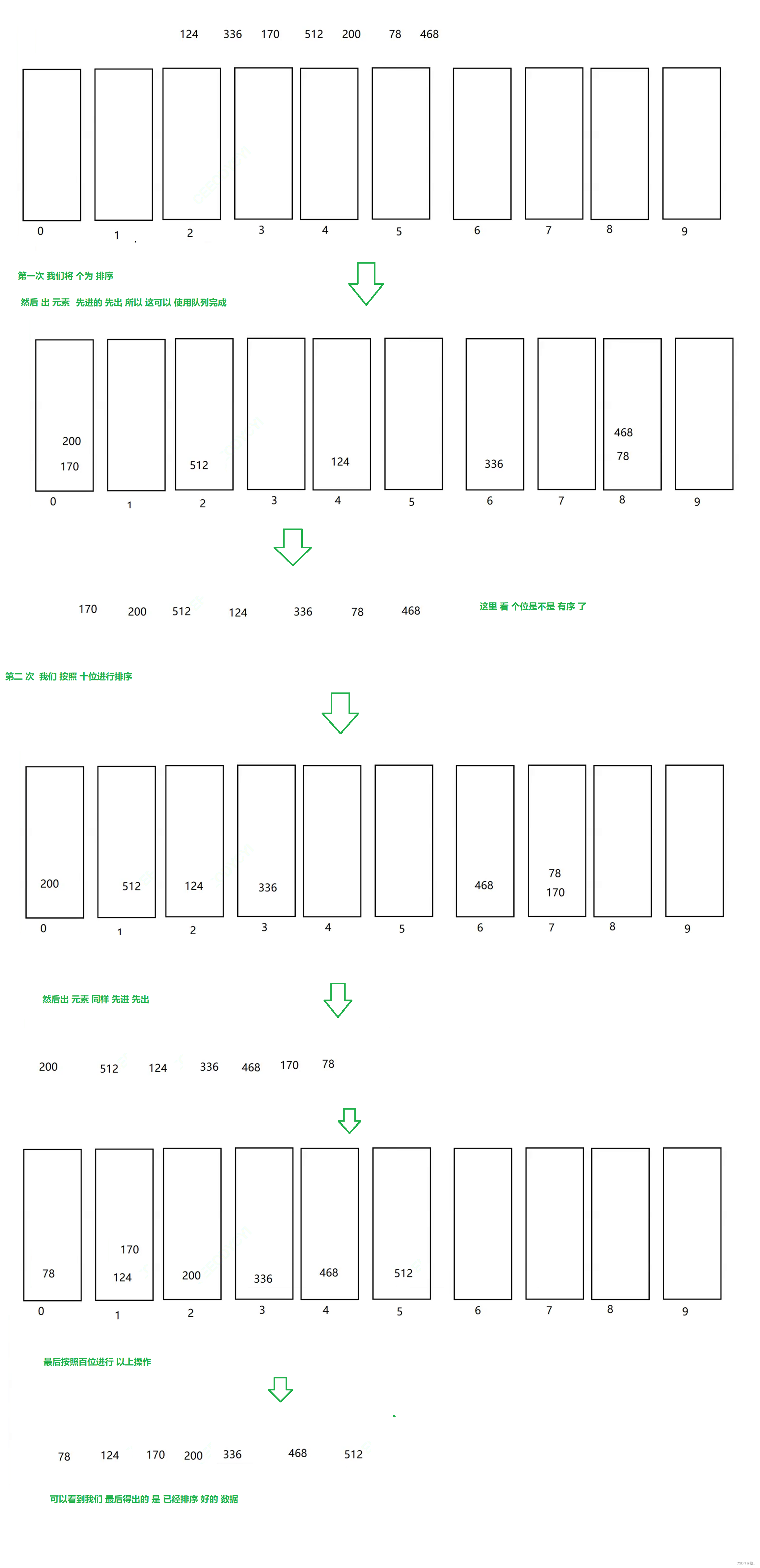
2.桶排序

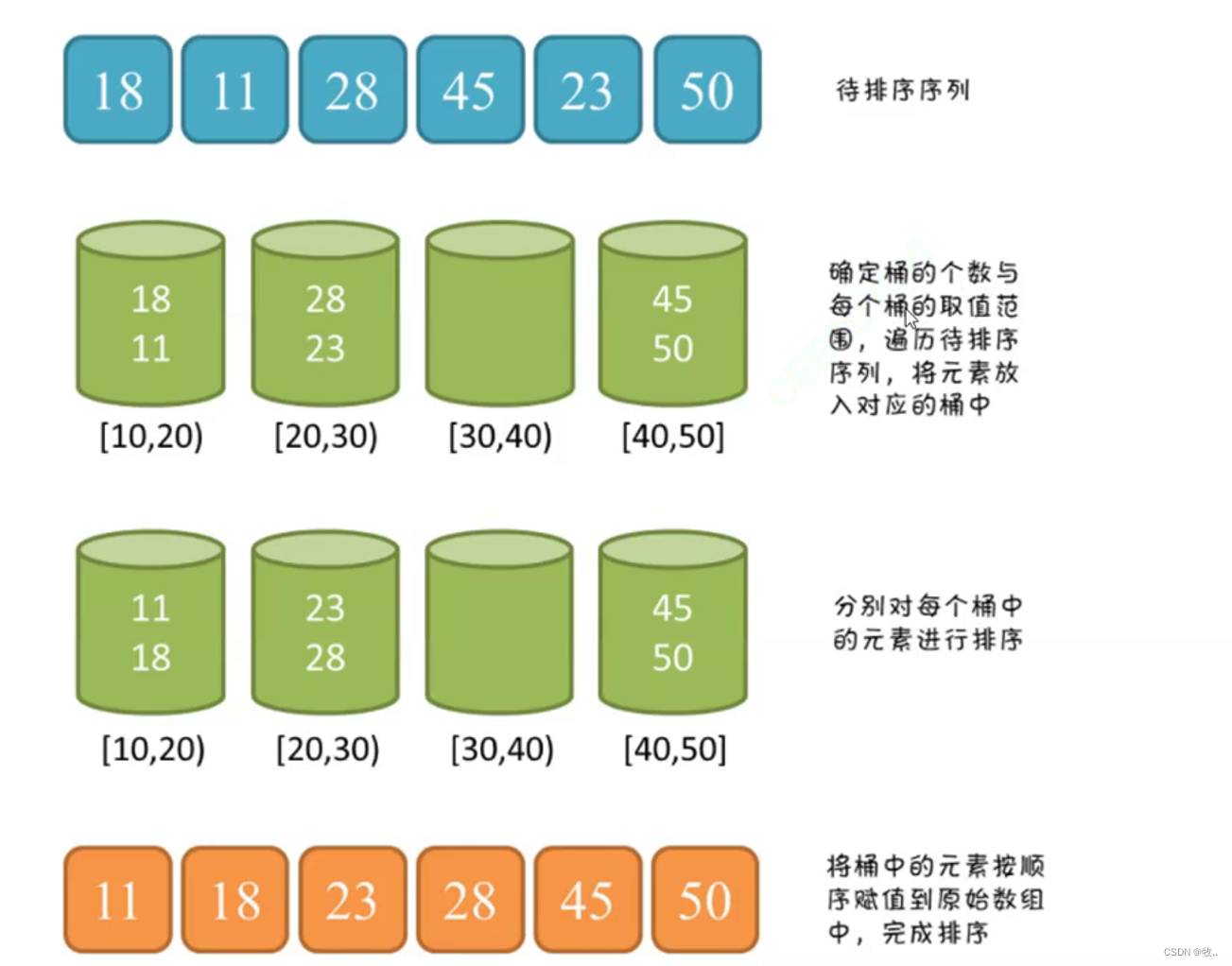
这里我们 只需要了解，那么 可以看别人 如何 写 的

桶排序)

3.计数排序

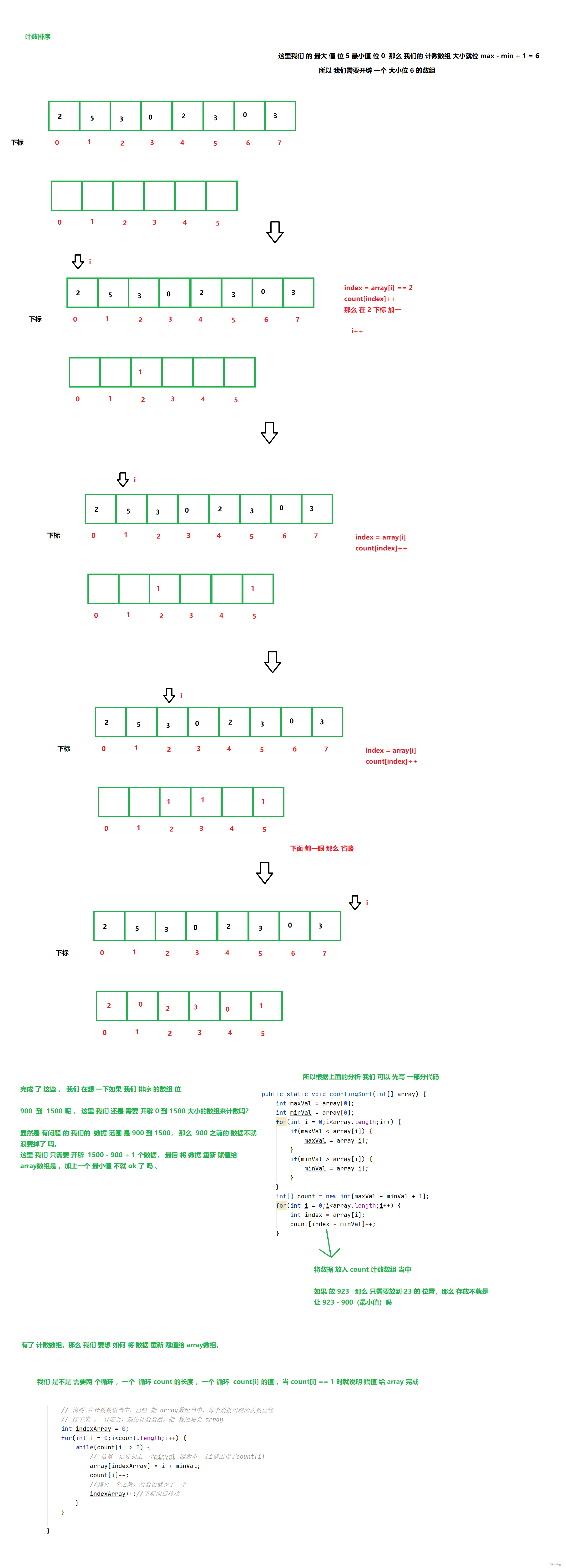
附上代码

                                                                              
  /**                                                                         
   * 计数排序                                                                     
   * 时间复杂度 O(N)                                                               
   * 这里 循环是 并列 的，这里 拿空间 换时间                                                   
   * 空间复杂度 与 计数的范围有关                                                          
   * O(M) M :代表当前数据的范围如 900 - 999                                             
   * 稳定性: 对当前 这个代码来说 是不稳定 的，但是 本质上 是 稳定的                                      
   * 一般适用于 有 n 个数 数据范围 0 - n 之间                                               
   */                                                                         
                                                                              
  public static void countingSort(int[] array) {                              
      int maxVal = array[0];                                                  
      int minVal = array[0];                                                  
      for(int i = 0;i<array.length;i++) {                                     
          if(maxVal < array[i]) {                                             
              maxVal = array[i];                                              
          }                                                                   
          if(minVal > array[i]) {                                             
              minVal = array[i];                                              
          }                                                                   
      }                                                                       
      int[] count = new int[maxVal - minVal + 1];                             
      for(int i = 0;i<array.length;i++) {                                     
          int index = array[i];                                               
          count[index - minVal]++;                                            
      }                                                                       
      // 说明 在计数数组当中，已经 把 array数组当中，每个数据出现的次数已经统计好了                            
      // 接下来 ， 只需要，遍历计数数组，把 数组写会 array                                        
      int indexArray = 0;                                                     
      for(int i = 0;i<count.length;i++) {                                     
          while(count[i] > 0) {                                               
              // 这里一定要加上一个minval 因为不一定i就出现了count[i]                           
              array[indexArray] = i + minVal;                                 
              count[i]--;                                                     
              //拷贝一个之后，次数也就少了一个                                               
              indexArray++;//下标向后移动                                           
          }                                                                   
      }                                                                       
                                                                              
  }                                                                           
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41