论文笔记：NAFNet: Simple Baselines for Image Restoration

作者：黑客灵魂 | 2024-07-13 02:16:22

踩

nafnet

向孙老师致敬！

方法

块内(Intra-block)结构比较：
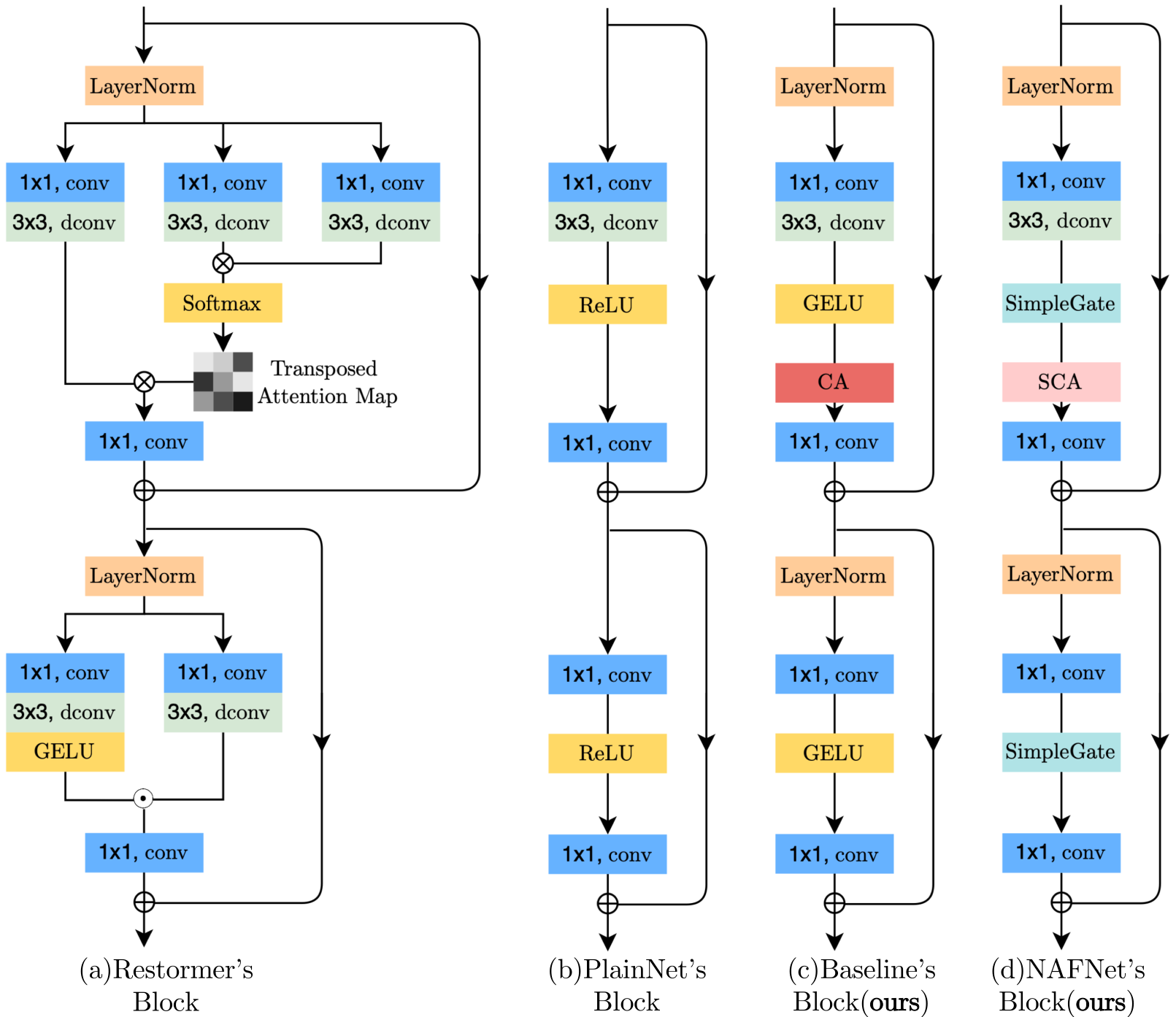
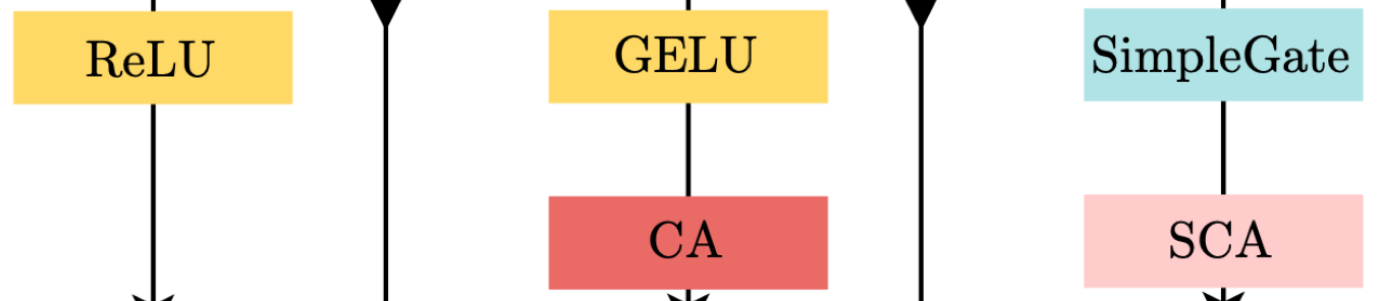
在这里插入图片描述
其中Channel Attention (CA)，Simplified Channel Attention(SCA)，从左到右依次替换

归一化：将层归一化(Layer Normalization)添加到普通块中，因为它可以稳定训练过程。

激活函数：在plain块中用GELU替换ReLU，因为它在保持图像去噪性能的同时，为图像去模糊带来了非平凡的收益。

注意力：通道注意力
在这里插入图片描述

Nonlinear Activation Free Network

在这里插入图片描述
Gated Linear Units： $\operatorname{Gate}(\mathbf{X}, f, g, \sigma)=f(\mathbf{X}) \odot \sigma(g(\mathbf{X}))$

GELU： $\Phi(x)$ ，其中 $Φ$ 表示标准正态分布的累积分布函数。GELU可以通过以下方式进行近似和实现 $x\left(1+\tanh \left[\sqrt{2 / \pi}\left(x+0.044715 x^{3}\right)\right]\right)$

我们提出了一个简单的GLU变体：直接将特征映射划分为通道维度的两部分，并将它们相乘 $\text { SimpleGate }(\mathbf{X}, \mathbf{Y})=\mathbf{X} \odot \mathbf{Y}$ 其中，X和Y是大小相同的特征映射。

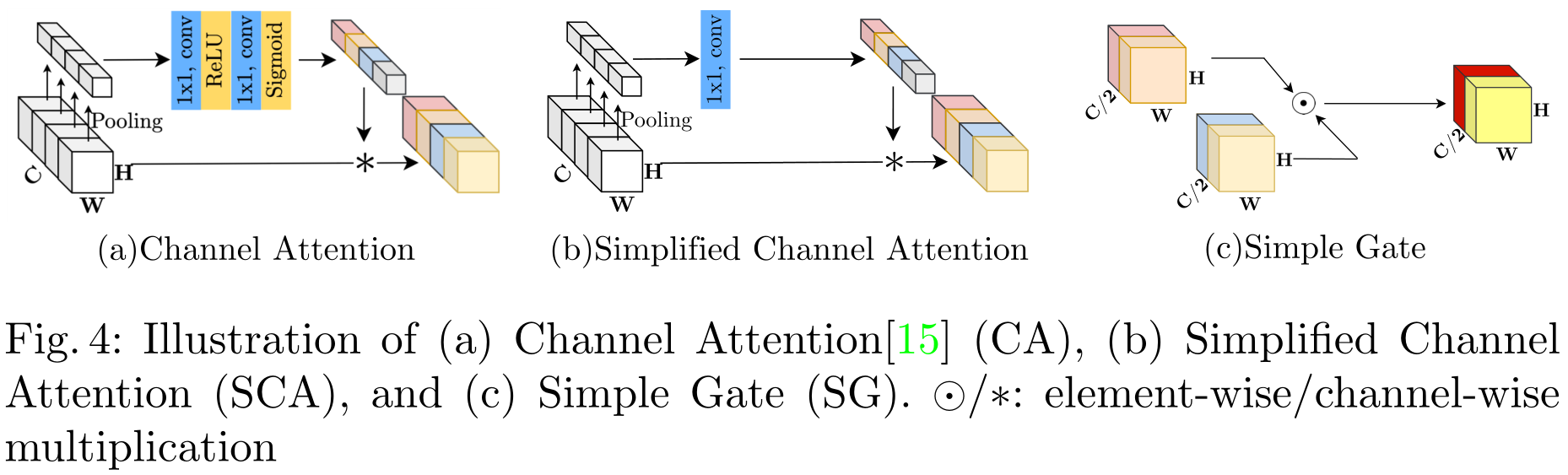
Simplified Channel Attention：使用的是SENet $A(\mathbf{X})=\mathbf{X} * \sigma\left(W_{2} \max \left(0, W_{1} \operatorname{pool}(\mathbf{X})\right)\right)$

其中X表示特征映射，pool表示将空间信息聚合到通道中的全局平均池化操作。 $σ$ 是一个非线性激活函数Sigmoid， $W_1$ 、 $W_2$ 是全连接层，两个全连接层之间采用ReLU，最后的 $*$ 是一种通道乘积运算(channelwise product operation)。简化的CA： $A(\mathbf{X})=\mathbf{X} * W \operatorname{pool}(\mathbf{X})$

本质上删除了激活函数。

实验

在这里插入图片描述

代码

github.com/megvii-research/NAFNet

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/黑客灵魂/article/detail/817179

论文笔记：NAFNet: Simple Baselines for Image Restoration

向孙老师致敬！

相关工作

方法

Nonlinear Activation Free Network

实验

代码